基于FLAC3D岩石应变软化模型的研究

周 勇，王 涛，b，吕 庆，朱远乐，王翔翔

（武汉大学a.水资源与水电工程科学国家重点实验室；b.水工岩石力学教育部重点实验室，武汉 430072）

基于FLAC3D岩石应变软化模型的研究

周 勇a，王 涛a，b，吕 庆a，朱远乐a，王翔翔a

（武汉大学a.水资源与水电工程科学国家重点实验室；b.水工岩石力学教育部重点实验室，武汉 430072）

在岩土工程的实践中，许多岩土体材料在载荷作用下表现出应变软化特性，因而在岩土工程数值模拟中如何更好地表现出岩土材料的应变软化特性非常关键。首先分析了“圆形孔洞问题”这一岩土工程领域的基本问题，并对该问题基于应变软化模型建立的现有理论解与FLAC3D的数值计算结果进行了对比，所得到的结果验证了FLAC3D应变软化模型在数值计算时的准确性和适用性。接着采用FLAC3D程序中的应变软化模型与理想弹塑性模型对该问题进行了计算，通过对计算结果的对比分析，认为忽略应变软化岩土材料的强度软化特性对工程是偏于危险的。最后对FLAC3D中应变软化模型的相关参数（εpi、残余系数）进行了研究。研究成果有助于研究人员更深入地理解岩石应变软化模型的力学本质。

应变软化；孔洞扩张；FLAC3D

1 研究背景

岩石在应力达到峰值强度之后，随着变形的继续增加，其强度迅速降到一个较低的水平，这种由于变形引起的岩石材料性能劣化的现象称之为“应变软化”。多年来岩土材料的应变软化问题一直为力学界和岩土工程界所关注，如何准确地描述岩土的应变软化已是岩土力学研究的难题［1］。

很多学者对应变软化理论及数值模型等方面进行了深入研究。文献［2］在1972年提出了含有应变软化段的弹塑性本构关系；文献［3］给出了完整的弹塑性本构积分的数值格式和增量型弹塑性有限元求解算法；文献［4］研究了围压对软岩峰后软化特性的影响和软岩的宏观物理参数峰后应变软化规律等；文献［5］对三峡花岗岩进行了常规三轴压缩试验，并基于弹塑性理论，根据试验数据拟合屈服面，研究花岗岩强度参数与峰后应变软化参量的关系，建立了花岗岩的峰后应变软化模型；文献［6］通过对软弱泥岩进行常规三轴压缩试验得到应力应变关系曲线，然后采用数值拟合的方法建立了广义黏聚力和广义内摩擦角等岩石峰后力学参数的软化规律，最后利用数值模拟方法进行了验证。

这些理论研究很大程度上加深了人们对岩石塑性应变软化特性的认识，对实际工程应用也起到了一定的推动作用。文献［7］研究了岩石应变软化模型在深埋隧洞数值分析中的应用，并且通过数值加载分析了Mohr-Coulomb弹塑性模型和应变软化模型，计算得到了岩石应力应变关系之间的区别；文献［8］提出了将应变软化过程简化为一系列的脆性应力跌落与塑性流动过程的思想，并将这种模拟应变软化过程的思想方法用于求解均匀初始应力场中应变软化介质内的圆形隧道开挖问题；文献［9］基于应变软化模型建立了一种简化程序应用于分析圆形隧洞的应力及位移分布特性等问题；文献［10］在有限元数值分析程序中，采用基于Mohr-Coulomb屈服准则的应变软化模型，对土质边坡稳定性进行了分析，并将结果与其它本构关系进行了对比，认为采用应变软化模型对土质边坡稳定性问题进行分析是比较合理的。目前岩土应变软化模型的应用在地下隧道工程等方面已经有较大发展，但在煤层开采、边坡稳定性分析等其他岩土工程领域还有待进一步的发展。

本文基于以上研究成果，分析了岩土体应变软化的一般特性和几种典型的简化模型。通过分析岩土工程领域的基本问题之一“圆形孔洞问题”，对该问题基于应变软化模型建立的现有理论解与FLAC3D的数值计算结果进行对比，来验证该数值计算方法的准确性和适用性。最后对FLAC3D中应变软化模型的特性进行了分析研究。

2 岩土应变软化特性与简化模型

岩土体的应力应变全过程曲线能够较好的反映岩土材料的物理力学特性［11］。图1为岩石在低侧限压缩条件下典型的应力应变关系曲线。该曲线包含了2个基本特征行为区间：弹性特征区间和非线性特征区间。其中弹性特性区间的应变量微小且可逆；而非线性区间的应变中包含着永久变形，这是因为在整个非线性阶段（包括峰前）中均有损伤（主要是微裂纹的形成及传播）的产生和积累。

图1 低侧限条件下岩石典型的应力－应变曲线Fig.1 Typical com pressive stress-strain curve of rock under low lateral confinement

峰后非线性阶段一般包含有脆性特征区间、软化特征区间及残余强度区间。岩石脆性特征表现为在达到峰值的瞬间其承载能力迅速下降的行为，整个过程的应变极小，但伴随有微裂纹的急剧扩展与集结；软化特征表现出一个承载能力持续降低的过程，且整个过程的变形量相对较大；残余强度阶段主要表现为岩体能够在低载荷作用下“无限期”的产生形变。

基于以上分析，并考虑到不同岩土体材料力学特性所表现出的差异，根据室内外岩土力学试验及广泛的岩体工程经验可以基于不同岩体类别将图1进行简化，岩土材料的本构关系可以划分为纯弹性（图2（a））、理想弹塑性（图2（b））、弹脆塑性（图2（c））、应变软化（图2（d））特性等几种本构关系，图2显示了4种基本的简化模型类型。有关前3种本构关系的研究方法与理论已经发展的非常成熟，而对于具有广泛应用价值的应变软化本构关系，由于其相对复杂使得在该方向的研究上还存在较多的困难需要解决。文献［12］建议将弹脆塑性本构（elastic-brittle-plastic）、应变软化本构（elastic-strain softening）和理想弹塑性本构（elastic-perfectly plastic）分别对应于岩体质量的很好、中等及很差等3种情况。

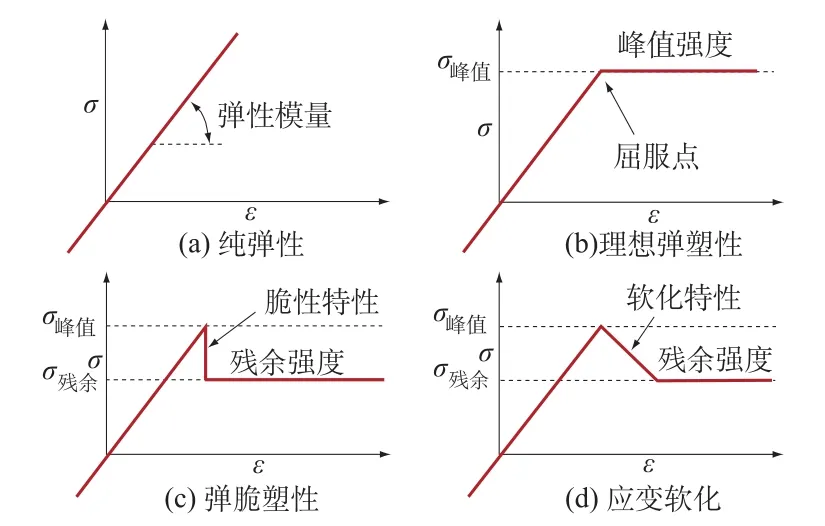
图2 几种简化的典型岩石应力－应变曲线Fig.2 Typical simplified stress-strain curves of rock

目前，利用基于三维显式有限差分法的FLAC3D可以对图2中所有类型的本构模型进行模拟，而且对于图1表示的复杂本构关系也可以通过采用编制相应程序后进行内嵌的方式进行相应的数值计算。

FLAC3D［13］中的应变软化模型是基于与剪切流动法则不相关联而与拉力流动法则相关联的Mohr-Coulomb屈服准则建立的一种本构模型。该模型与理想弹塑性本构模型的差别在于塑性屈服开始后，黏聚力、摩擦角、剪涨扩容和抗拉强度可能会发生变化，由此在数值模拟计算过程中反映出岩土体的应变软化特性。

3 应变软化模型数值验证——“孔洞扩张问题”

在岩土工程的实践中，多数岩、土体材料在工程载荷作用下表现出应变软化特性，因此研究某类工程基本问题在应变软化条件下的解析解或者研究模拟应变软化行为的数值方法具有很重要的理论价值和工程意义。

“圆形孔洞问题”作为岩土工程领域的基本问题之一，长期受到研究者的广泛关注。其研究意义不仅在于对岩土工程中可以简化为类似问题的变形预测与支护设计有指导意义（如圆形巷道和硐室等的稳定、石油工程中的井壁稳定和岩土力学中的扩孔等问题等），而且由于研究对象相对简单，该研究成果又能够作为检验数值分析方法及程序正确与否的经典考题［8］。

3.1 “孔洞扩张问题”概述

由于孔壁处受到内压力pi的作用，岩土体产生扩张，孔周围岩体经历3个阶段：当pi较小时，岩土体处于弹性阶段；当pi继续增大并达到一定值时，孔壁附近岩土体进入软化阶段；随着pi继续增大，孔壁附近岩土体又进入残余强度阶段，最终在孔周围形成残余强度区、软化区、弹性区，其中残余强度区与软化区构成了整个塑性区。图3显示了一个在初始处于弹性状态的连续均匀各向同性介质的圆形孔洞，其内壁受到均匀内压pi作用时孔口附近岩土体的物理力学状态。

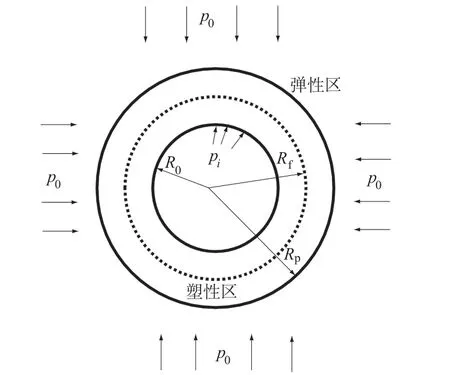
图3 无限区域介质内的“圆形孔洞问题”Fig.3 Circular cavity in an infinitemedium

虽然“圆形孔洞问题”在有关其物理力学机理的研究中进行了很多简化（如承受均匀地应力作用，圆形规则孔洞，考虑成平面应变问题等），但在探求其考虑应变软化条件下解析解的问题上却仍遇到了很多困难。这主要由于模拟应变软化本构关系时，其峰值后区为负斜率，导致传统弹塑性理论中增量应力－应变矩阵出现奇异或负定，从而使得数值解变得不稳定或者不可解［14］。同时应变软化过程中应力、塑性应变与强度参数之间关系非常复杂，如果多个材料强度参数分别发生变化，就更难给出此类应变软化问题的解析解。

目前，在“孔洞扩张问题”研究方面，主要是基于简化的“三折线”应变软化模型进行研究，图4给出了在“三折线”假设条件下应变软化模型的应力应变关系曲线。文献［15－16］采用Mohr-Coulomb屈服准则对土体孔洞扩张过程中的扩展压力、位移与塑性区等进行了分析。文献［17］采用经典弹塑性理论，通过求自相似解（self-similar solutions，此方法不需求出显式表达形式的解）的方法，分析了圆形洞室问题在应变软化介质中的地层反应曲线（ground reaction curve）以及软化区与残余强度区的范围。文献［18］基于Tresca屈服准则给出了应变软化特性材料中“孔洞扩张问题”的理论解。

3.2 基于应变软化Tresca材料的“孔洞扩张问题”理论解

文献［18］基于图3和图4进行了“孔洞扩张问题”数值解的推导。图4中，参数β，f和h的值可由三轴压缩试验测得。其中f，h为非负的比例系数，其值在等于1、大于1和小于1时，分别对应于材料不可压缩、剪胀和剪缩的特性。Rf，Rp分别为残余强度区、软化区、弹性区三者之间的交界面半径。根据受力特点，此类问题可按平面应变问题求解，σr，σθ分别与σ1，σ3相对应，应变符号及对应关系类同。

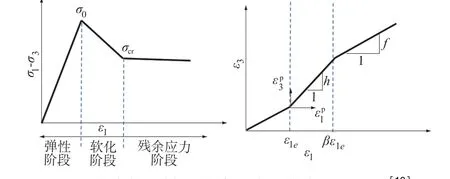
图4 应变软化模型的简化应力应变关系曲线［19］Fig.4 Sim plified stress-strain curves of strain softeningmodel［19］

根据Tresca屈服准则，材料屈服函数为

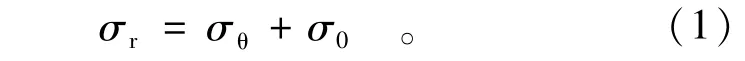
在初始屈服时，式中σ0＝2C0，C0为材料的凝聚力。在应变软化区内，σ0＝2C0－λεpr，εpr为软化区内的径向塑性应变；在塑性流动区，σ0＝2Ccr，Ccr为材料的残余凝聚力。

文献［18］中考虑应变软化特性Tresca材料的扩孔问题解析解的部分结果如下。

残余强度区的位移场与应力场为

式中：ur为径向位移；B＝（1＋v）C0／E，E为材料的名义弹性模量；v为材料的泊松比。

残余强度区和应变软化区的半径之比为

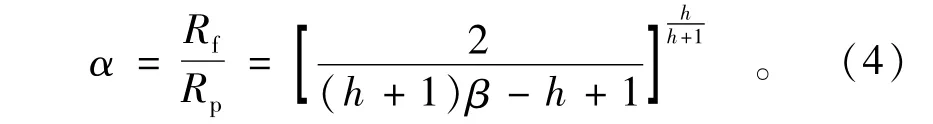
残余强度区的半径为

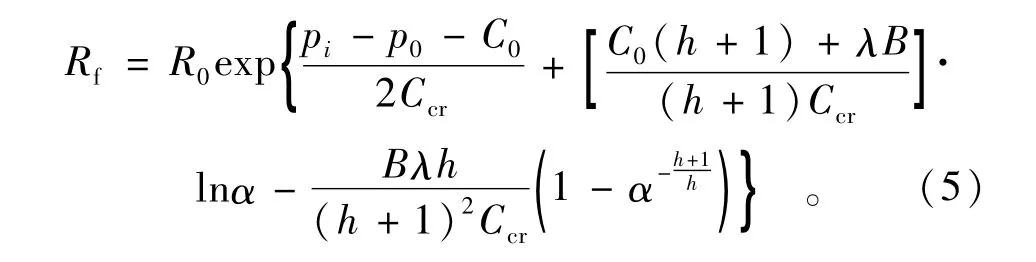
式中λ＝2（C0－Ccr）／［（β－1）B］。

孔周进入流动区的最小扩孔压力为

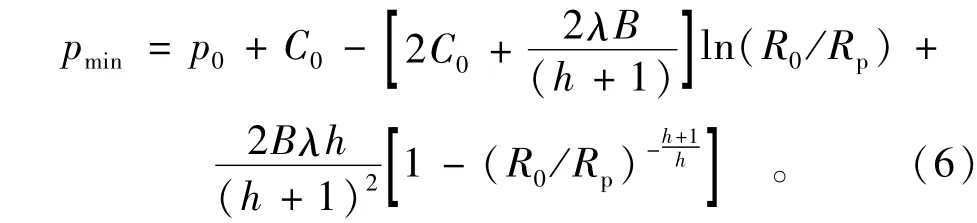
3.3 算例验证与分析

为了验证采用基于FLAC3D程序的应变软化模型进行数值计算时的准确性和适用性，根据以上建立的基于应变软化Tresca材料的“孔洞扩张问题”理论解与FLAC3D数值计算结果进行对比分析是十分有必要且可行的。下文以一个简单的力学分析模型为例进行对比分析。

模拟圆形孔洞扩张问题，为了便于分析对比和计算，孔洞的半径设为1 m，外周界压力p0为0 MPa。模型的材料参数设定如下：材料的弹性模量E为250 MPa；泊松比v为0.25，凝聚力C0取0.5 MPa；残余凝聚力Ccr取0.45 MPa；f和h均取为1；β取为1.468 8。由于研究对象是基于Tresca屈服准则，内摩擦角和剪胀角均可取为0。

采用以上参数，根据公式（1）至（6）可以计算得到该模型的具体解析解结果，本文中主要分析了2种方案的位移分布及塑性区分布情况。如图7为绘制的围岩特性曲线图（其中横坐标Pi／C0为内压力与材料凝聚力之比，纵坐标ru为孔洞内壁径向位移），图8为Rp／R0与Pi／C0关系曲线图（其中纵坐标Rp／R0为塑性区半径与孔洞半径之比）。

FLAC3D数值计算模型的建立：利用FLAC3D数值计算程序，建立了如图5所示的圆形孔口扩展模型，模型的尺寸、采用的材料参数均与力学分析模型相同或等效。有关“三折线”应变软化模型，在FLAC3D程序中可以采用式（7）表示其峰后应力应变关系：

式中：残余系数η＝Ccr／C0，可反映后区应力跌落的程度，εp1为软化阶段与残余应力阶段交界点处的总塑性应变，算例中“孔洞扩张问题”理论解中的β取1.468 8时通过相应公式转换可等效于FLAC3D程序中εp1＝1.875×10－3。

图5 简化计算模型Fig.5 Simplified calculation model

为了保证数值计算的可操作性和合理性，模型的外围半径取值足够大（为20 m），整个模型共有4 560个网格。数值模拟过程中通过采用逐渐增大的内压力pi分别进行计算，最后可得到多组工况下应变软化材料的变形与塑性区分布等数值计算结果。本文为了回避软化过程中的分叉或局部化问题，将内压力pi的值放置在一个合适的范围内进行计算。具体数值计算结果详见图6和图7。

图6 不同条件下的塑性区半径分布情况Fig.6 Change of p lastic zone radiiw ith different internal pressures

图7 不同内压力条件下的围岩特性曲线Fig.7 Ground reaction curve w ith different internal pressures

通过对比图6和图7中的应变软化模型理论解与FLAC3D数值计算结果：发现2种方法所得的塑性区半径非常吻合，虽然数值解结果曲线是基于Tresca屈服准则绘出的，FLAC3D进行数值计算中采用的应变软化模型却是基于Mohr-Coulomb屈服准则条件的，但考虑到Tresca屈服准则是Mohr-Coulomb屈服准则在不考虑内摩擦角时的特例，故得出以上结果是完全可以理解的；对于孔壁径向位移分布情况（孔洞围岩特征曲线），FLAC3D数值计算结果在内压力pi较小时与理论解十分接近，随着pi的增加，数值计算结果相对理论结果有一定的偏差，但偏差相对较小（约为10%），究其原因是FLAC3D数值计算结果受到网格的密度和分布形态及边界条件的影响较大，当pi过大时该模型计算的结果可能会有所偏差；2种方式计算的最小扩孔压力基本一致，pmin约为0.68 MPa。

4 FLAC3D中应变软化模型特性分析

4.1 FLAC3D的应变软化模型与理想弹塑性模型的对比分析

为了进一步研究FLAC3D中应变软化模型的特性，将该计算结果与FLAC3D中的理想弹塑性本构模型（Mohr-Coulomb本构模型）进行了对比分析。基于上节建立的几何模型，采用理想弹塑性本构模型进行计算，绘制其与采用应变软化模型计算所得结果的对比图，如图8和图9所示。

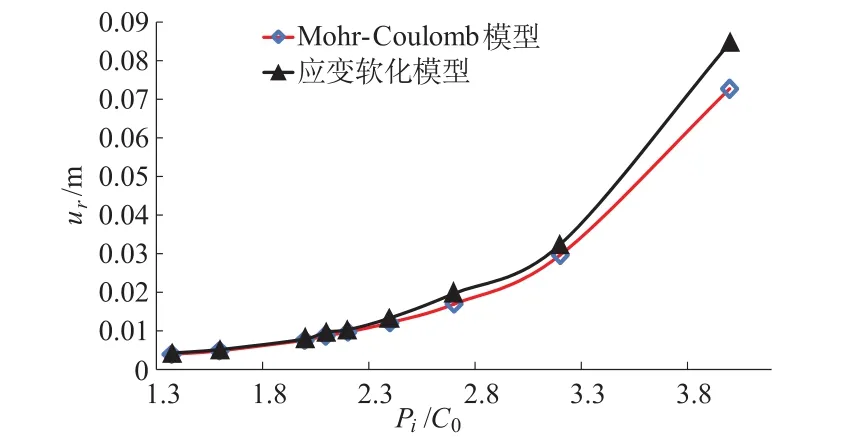
图8 理想弹塑性本构模型与应变软化模型围岩特性曲线Fig.8 Ground reaction curves of M ohr-Coulomb model and strain softening model

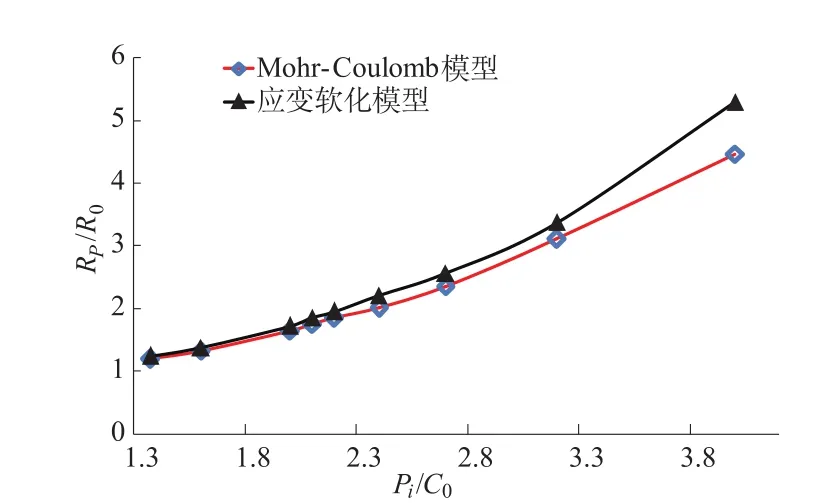
图9 理想弹塑性本构模型与应变软化模型塑性区半径分布情况Fig.9 Change of plastic zone radii of M ohr-Coulomb model and strain softening model

通过图8和图9中的对比分析，不难发现采用应变软化模型计算出的塑性区半径比采用理想弹塑性本构模型时要大，且孔洞内壁的径向位移也相对较大。

应变软化模型与理想弹塑性本构模型对比分析研究结果表明，对于应变软化岩土材料，忽略其强度软化特性对工程是偏于危险的，采用应变软化模型可能会更加合理的反映围岩的应力、变形情况。

4.2 FLAC3D中应变软化模型的相关参数研究

基于上节建立的几何模型，现就FLAC3D的应变软化模型中几个重要参数进行分析。

当εp1＝1.875×10－3时，取不同的残余系数η＝Ccr／C0，进行“孔洞扩张问题”数值模拟，计算结果如图10和图11所示。

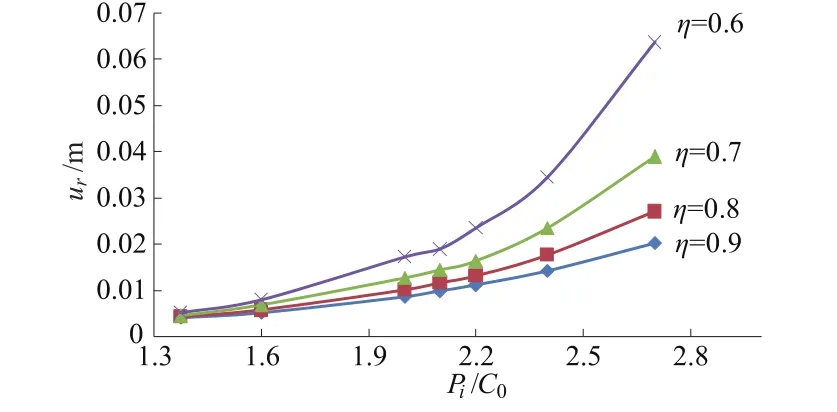
图10 不同η条件下的围岩特性曲线Fig.10 Ground reaction curves w ith differentηvalues

图11 不同η条件下的塑性区半径分布情况Fig.11 Change of plastic zone radiiw ith differentηvalues

图10和图11中的结果显示：残余系数η对“孔口扩张问题”的塑性区半径及孔壁径向位移的影响十分明显。随着η的增加，塑性区半径及孔壁径向位移均有较大幅度的减小，且内压pi越大时影响越明显。由此可见残余系数η的取值十分关键，对模型的位移和塑性区分布均起到十分明显的作用。

当残余系数η＝Ccr／C0＝0.9时，通过调整εp1的值，进行了多组数值计算试验，部分结果如图12所示。结果表明：εp1的变化对“孔口扩张问题”的塑性区半径及孔壁径向位移的影响很小。图12显示εp1大幅增加（1.875×10－3→2.5×10－2）时，孔壁径向位移也只有大约10%左右的下降，且整个变化过程中塑性区半径变化很小。

图12 不同条件下的围岩特性曲线Fig.12 Ground reaction curves w ith differentvalues

5 结 论

（1）本文通过分析岩土工程领域的基本问题之一“圆形孔洞问题”，对该问题基于应变软化模型建立的现有理论解与FLAC3D的数值计算结果进行对比，所得到的结果在一定程度上验证了采用FLAC3D中的应变软化模型进行数值计算时的准确性和适用性。

（2）采用数值计算方法进行岩土工程问题模拟时，通过对应变软化模型与理想弹塑性本构模型的对比分析，可知忽略应变软化岩土材料的强度软化特性对工程是偏于危险的。

（3）通过对FLAC3D中应变软化模型的相关参数（εp1、残余系数η）进行了研究：发现残余系数η与数值模拟中的位移及塑性区分布等关键表征参量有着很强的相关性，而塑性应变指标εp1对这些表征参量的影响相对较小。这些规律对数值计算中的参数取值问题有一定的指导意义。

［1］ 沈珠江.土体结构性的数学模型——21世纪土力学的核心问题［J］.岩土工程学报，1996，18（1）：95－97.（SHEN Zhu-jiang.Mathematical Modeling of Soil Structure：The Key Problem of Soil Mechanics in 21st Century［J］.Chinese Journal of Geotechnical Engineering，1996，18（1）：95－97.（in Chinese））

［2］ NAYAK G C，ZIENKIEWICZ O C.Elastic-plastic Stress Analysis，A Generalization for Various Constitutive Relations Including Strain-Softening［J］.International Journal for Numerical Methods in Engineering，1972，5：113－135.

［3］ 沈新普，岑章志，徐秉业.弹脆塑性软化本构理论的特点及其数值计算［J］.清华大学学报，1995，35（2）：22－27.（SHEN Xin-pu，CEN Zhang-zhi，XU Bing-ye.Features and Numerical Calculation of the Elastic-Brittle-Plastic Softening Constitutive Theory［J］.Tsinghua University Journals，1995，35（2）：22－27.（in Chinese））

［4］ 杨 超，崔新明，徐水平.软岩应变软化数值模型的建立与研究［J］.岩土力学，2002，23（6）：695－697，701.（YANG Chao，CUI Xin-ming，XU Shui-ping.Establishment and Study of Strain Softening Numerical Constitutive Model for Soft Rock［J］.Rock and SoilMechanics，2002，23（6）：695－697，701.（in Chinese））

［5］ 张 帆，盛 谦，朱泽奇，等.三峡花岗岩峰后力学特性及应变软化模型研究［J］.岩石力学与工程学报，2008，27（增1）：2651－2655.（ZHANG Fan，SHENG Qian，ZHU Ze-qi，et al.Study on Post-peak Mechanical Behaviour and Strain-Softening Model of Three Gorges Granite［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（Sup.1）：2651－2655.（in Chinese））

［6］ 陆银龙，王连国，杨 峰，等.软弱岩石峰后应变软化力学特性研究［J］.岩石力学与工程学报，2010，29（3）：640－648.（LU Yin-long，WANG Lian-guo，YANG Feng，etal.Post-peak Strain Softening Mechanical Properties ofWeak Rock［J］.Chinese Journalof Rock Mechanics and Engineering，2010，29（3）：640－648.（in Chinese））

［7］ 周家文，徐卫亚，李明卫，等.岩石应变软化模型在深埋隧洞数值分析中的应用［J］.岩石力学与工程学报，2009，28（6）：1116－1127.（ZHOU Jia-wen，XUWei-ya，LIMing-wei，et al.Application of Rock Strain Softening Model to Numerical Analysis of Deep Tunnel［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（6）：1116－1127.（in Chinese））

［8］ 王水林，吴振君，李春光，等.应变软化模拟与圆形隧道衬砌分析［J］.岩土力学，2010，31（6）：1929－1936.（WANG Shui-lin，WU Zhen-jun，LIChun-guang，et al.Modeling of Strain-Softening and Analysis of a Lining for Circular Tunnel［J］.Rock and Soil Mechanics，2010，31（6）：1929－1936.（in Chinese））

［9］ PARK K H，TONTAVANICH B，LEE JG.A Simple Procedure for Ground Response Curve of Circular Tunnel in E-lastic-Strain Softening Rock Masses［J］.Tunnelling and Underground Space Technology，2008，23：151－159.

［10］CONTEE，SILVESTRIF，TRONCONE A.Stability Analysis of Slopes in Soilswith Strain-Softening Behaviour［J］.Computers and Geotechnics，2010，37：710－722.

［11］EGGER P.Design and Construction Aspects of Deep Tunnel（with Particular Emphasis on Strain Softening Rocks）［J］.Tunnelling and Underground Space Technology，2000，15（4）：403－409.

［12］HOEK E，BROWN E T.Practical Estimates of Rock Mass Strength［J］.International Journal of Rock Mechanics Mining Sciences，1997，34（8）：1165－1186.

［13］Itasca Consulting Group Inc.2006.FLAC3D—Fast Lagrangian Analysis of Continua in 3 Dimensions.Ver.3.1 User’s Manual［K］.Minneapolis：ICG.

［14］赵启林，牛海清，卓家寿.应变软化材料的几个基本问题研究进展［J］.水利水运工程学报，2001，（3）：73－77.（ZHAO Qi-lin，NIU Hai-qing，ZHUO Jia-shou.Basic Problems of Strain-Softening Material［J］.Hydro-science and Engineering，2001，（3）：73－77.（in Chinese））

［15］王晓鸿，王家来，梁发云.应变软化岩土材料内扩孔问题解析解［J］.工程力学，1999，16（5）：71－76.（WANG Xiao-hong，WANG Jia-lai，LIANG Fa-yun.Analytical Solution to Expansion of Cavity in Strain-Softening Materials［J］.Engineering Mechanics，1999，16（5）：71－76.（in Chinese））

［16］蒋明镜，沈珠江.考虑剪胀的线性软化柱形孔扩张问题［J］.岩石力学与工程学报，1997，16（6）：550－557.（JIANG Ming-jing，SHEN Zhu-jiang.On Expansion of Cylindrical Cavity with Linear Softening and Shear Dilation Behavior［J］.Chinese Journal of Rock Mechanics and Engineering，1997，16（6）：550－557.（in Chinese））

［17］ALONSO E，ALEJANO L R，VARAS F，et al.Ground Response Curves for Rock Masses Exhibiting Strain-Softening Behaviour［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2003，27（13）：1153－1185.

［18］梁发云，陈龙珠.应变软化Tresca材料中扩孔问题解答及其应用［J］.岩土力学，2004，25（2）：261－265.（LIANG Fa-yun，CHEN Long-zhu.Analytical Solution to Cavity Expansion in Strain-Softening Soils with Tresca Yield Criterion and Its Applications［J］.Rock and Soil Mechanics，2004，25（2）：261－265.（in Chinese））

［19］BROWN E T，BRAY JW，LADANYIB，et al.Ground Response Curves for Rock Tunnels［J］.Journal of Geotechnical Engineering of ASCE，1983，109：15－39.

（编辑：赵卫兵）

Strain Softening M odel of Rock Based on FLAC3D

ZHOU Yong1，WANG Tao1，2，LV Qing1，ZHU Yuan-le1，WANG Xiang-xiang1
（1.State Key Laboratory ofWater Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；2.Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of MOE，Wuhan University，Wuhan 430072，China）

Many of rock and soilmaterials exhibit strain softening behaviour under load in geotechnical engineering practice.To show the strain softening properties of geotechnicalmaterial is crucial in the numerical simulation of geotechnical engineering.Based on previous researches，the authors analyze the circular cavity expansion problem which is one of the basic problems in geotechnical engineering，and compares the results of theoretical solution of strain softeningmodelwith FLAC3Dnumerical calculations.The comparison confirms the accuracy and applicability of strain softeningmodel in FLAC3Dnumerical calculation.Moreover，the numerical results obtained from computations by strain softeningmodel and elastic-perfectly plastic constitutivemodel are compared.Results show that the strength softening of strain softening geotechnicalmaterials could not afford to be ignored.Finally，the related parameters（εpiandη）of strain softeningmodel are analyzed.The research results could help researchers understand the nature ofmechanics in strain softeningmodel of rocks in the numerical calculation.

strain softening；cavity expansion；FLAC3D

TU452

A

1001－5485（2012）05－0051－06

2011－05－03；

2011－07－13

国家自然科学基金（51079111，50879063）；国家自然科学基金重大研究计划资助项目（90715042）

周 勇（1987－），男，湖北石首人，硕士研究生，主要从事工程地质和岩土力学方面的研究工作，（电话）13871511155（电子信箱）wuhanstudy＠sohu.com。