卡基娃面板堆石坝非线性强度指标坝坡稳定与可靠性研究

郑田中，王万千，李啸啸，罗文广，陈建康

（1.温州市堤塘河道管理处，浙江温州 325000；2.四川大学水利水电工程学院，成都 610065）

卡基娃面板堆石坝非线性强度指标坝坡稳定与可靠性研究

郑田中1，王万千2，李啸啸2，罗文广2，陈建康2

（1.温州市堤塘河道管理处，浙江温州 325000；2.四川大学水利水电工程学院，成都 610065）

针对目前在建和拟建的大型面板堆石坝地质条件差、地震烈度高、坝高不断增加的情况，解决一些比较突出的关键技术问题的重要性和迫切性日益突出。通过极限平衡理论和可靠度理论2种方法对属200m级高堆石坝范畴的卡基娃面板堆石坝进行坝坡稳定计算，研究了其非线性强度指标坝坡稳定及可靠度，分析了相关关键技术指标、安全系数标准对坝坡稳定安全的影响及可靠性水平等关键问题。与极限平衡理论相比，采用基于可靠度理论的方法设计坝坡，可以量化安全裕度，有利于高堆石坝坝坡的优化设计，这无疑对于减少工程投资和环境保护都具有极大的现实意义。

极限平衡法；可靠度；坝坡稳定；卡基娃面板堆石坝

对于土石坝坝坡稳定的分析，现在已经有许多种有效的方法。目前，学术界和工程界经常采用的研究方法主要有2种：一是以极限平衡理论为基础的条分法；二是以弹性理论为基础的有限元法［1］。以极限平衡理论为基础的条分法是经典的确定性分析方法，已在工程界广泛应用。极限平衡理论的运用现已十分成熟，其具有模型简单，计算简洁，能考虑多种加载方式和各种复杂剖面形状的优点［2－4］。目前常应用的有以下几种极限平衡分析方法，如：毕肖普法（Bishop）、瑞典圆弧法、Morgenstern-Prince法、简布法、楔体极限平衡分析法、余推力法、Sarma法等［5－6］。在土石坝工程中，对于坝坡稳定的传统评价指标是安全系数。但由于筑坝材料多为不同性质的土体，其本身性质具有较大的不确定性，在安全系数的求解过程中没有考虑材料的变异性、离散性、各向异性以及材料强度之间的相关性，因此出现了即使安全系数满足规范要求的边坡依然有可能出现失稳的问题［7］。因此，利用可靠性来分析坝坡的稳定性，能充分考虑材料性质的不确定性及离散性，得到边坡可靠度指标，从而保证稳定分析更加全面、更加准确。

1 安全系数与可靠度求解方法

1.1 安全系数求解方法及其特点

本文所用的以极限平衡理论为基础的条分法为：瑞典圆弧法和简化毕肖普法。

（1）瑞典圆弧法不考虑条间力对安全系数的影响，其安全系数按式（1）［8］计算。

（2）简化毕肖普法考虑了条间力的影响，其安全系数按式（2）计算［8］。

式（1）和式（2）中：W为土条重量；Q，V分别为水平和垂直地震惯性力；u为作用于土条底面的孔隙压力；α为条块重力线与通过此条块底面中点的半径之间的夹角；b为土条宽度；c＇，φ＇为土条底面的有效抗剪强度指标；Mc为水平地震惯性力对圆心的力矩；R为圆弧半径。

上下游坡外水位按置换法处理。

1.2 非线性强度指标安全系数计算方法

非线性强度指标的安全系数仍可按上述方法计算，只是安全系数的计算公式中考虑非线性抗剪强度的土条的凝聚力取0，而摩擦角按式（3）至式（6）确定。

式（3）至式（6）中：φ0，Δφ为土条底面的非线性抗剪强度指标；pa为一个标准大气压；φf为土体破坏时的摩擦角；σn为简化毕肖普法的土条底面正应力；σ3为土条底面的小主应力。

1.3 可靠度求解方法及其特点

基于瑞典法、简化毕肖普法、邓肯非线性抗剪强度准则和广义可行方向法（Generalized Feasible Direction Method，缩写为GFDM）的高堆石坝坝坡稳定可靠度计算的混合迭代法［9］（Mixed Iteration Method，缩写为MIM），运用边坡稳定安全系数及可靠度计算软件SCU-SLIDE进行可靠度计算，该软件能考虑随机变量相关性和概率分布截尾的影响，计算精度高；可自动搜索边坡最小可靠指标及其相应临界滑弧位置；能完成竣工、稳定渗流、库水位骤降及地震等各种工况的坝坡稳定可靠度分析。

1.3.1 坝坡稳定可靠度分析的功能函数

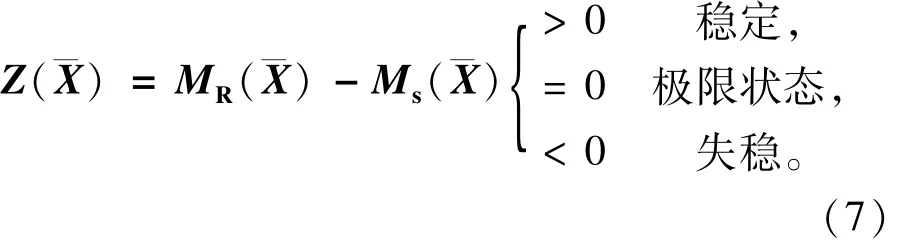
式中：¯X为随机向量；MR（¯X），Ms（¯X）分别为令安全系数Fs＝1时的整体抗滑力矩和整体滑动力矩。

该方式构建的功能函数可以直接对随机变量求偏导，有利于可靠度计算，因此，按该方式构建坝坡稳定的功能函数如下。

瑞典法：

简化毕肖普法：

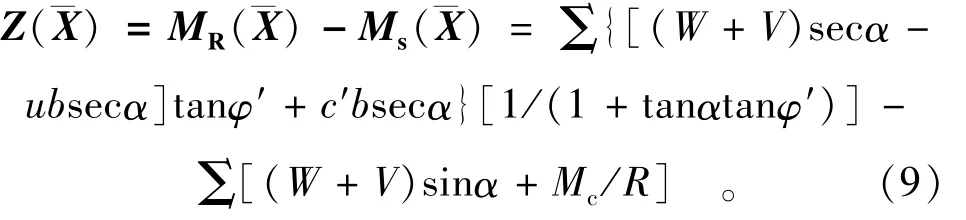
1.3.2 广义可行方向法（GFDM）

通过在广义随机空间中直接建立可行方向法迭代公式，提出了可靠度计算的广义可行方向法（GFDM），该方法具有容易处理相关随机变量、计算过程简单和收敛性好的优点。

β按式（10）计算：

其中x*为原始广义随机空间中与点Xk＋1对应的验算点，

1.3.3 功能函数及其对随机变量偏导数的计算

MIM由于在GFDM迭代计算可靠指标的过程中，同时需要迭代计算功能函数值和功能函数对随机变量的偏导数，因此，称为混合迭代法。

1.3.3.1 功能函数值的迭代计算

滑弧穿过了采用非线性强度参数的土层，那么对于式（1）或式（2）中考虑非线性强度的土条，应令其c＝0，而φ按（12）式确定。

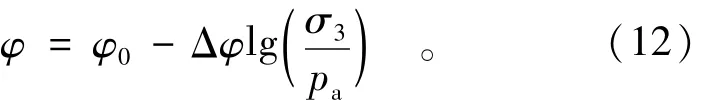
式中的φ0和Δφ应代入其新一轮迭代值，小主应力为

其中σn为土条底面的正应力，在瑞典法中

在简化毕肖普法中则为

因式（12）中含有未知变量φ，所以需要在式（12）和式（13）之间进行迭代计算直至如下式（16）的收敛条件得到满足。

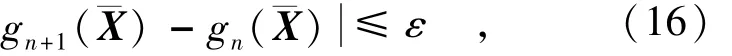
式（16）中：gn＋1（¯X），gn（¯X）分别为功能函数值的第n＋1次和第n次迭代值；ε是给定的容许误差。

1.3.3.2 功能函数对随机变量的偏导数

功能函数对随机变量偏导数的计算分为2种情况：

（1）当滑弧穿过采用线性强度指标的土层时，则计算功能函数在设计验算点处对c，φ的偏导数。

对于瑞典法：

对于简化毕肖普法：

式（17）至式（20）中的符号∑表示对所有考虑c，φ随机性的土条求和。

（2）当滑弧穿过采用非线性强度指标的土层时，则计算功能函数在设计验算点处对φ0，Δφ的偏导数。根据复合函数求导法则，由式（12）、（17）和（19）可得以下计算公式。

对于瑞典法：

对于简化毕肖普法：

式（21）至式（24）中的符号∑表示对所有考虑φ0，Δφ随机性的土条求和；式（22）和（24）中的小主应力σ3伴随功能函数值的迭代计算确定。

表1 坝坡稳定计算参数Table 1 Parameters of the slope stability calculation

2 工程实例分析

2.1 工程概况

卡基娃水电站水库正常蓄水位为2 850.00 m，正常蓄水位以下库容3.583亿m3，拦河大坝为面板堆石坝，最大坝高171 m，装机容量440 MW（不含生态小电站）。面板坝坝顶高程2 856.00 m，坝顶宽11 m，坝顶长323 m，上游坝坡为1∶1.4。下游坝坡设置2级宽5 m的马道，2 802.00 m高程以上下游坝坡为1∶1.5，2 802.00 m高程以下下游坡均为1∶1.4。大坝自上游至下游依次为弃渣压重区、黏土铺盖区、垫层区、过渡区、主堆石区、次堆石区、大块石护坡、下游压重区等。

2.2 坝坡稳定安全系数及可靠度计算成果分析

2.2.1 计算工况及参数选择

根据《混凝土面板堆石坝设计规范》（SL228—98）、《碾压式土石坝设计规范》（SL274—2001）的规定和工程实际情况，卡基娃面板堆石坝坝坡稳定计算考虑施工工况、稳定渗流工况、地震工况3种工况。

地震工况按下面3种情况考虑：①正常蓄水位＋设计地震：地震加速度基准值为50年内超越概率10%，相应的基岩地震水平动峰值加速度ah＝149 cm／s2，相应动态分布系数取3.0，地震作用效应折减系数取0.25；②正常蓄水位＋校核地震：地震加速度基准值为100年内超越概率2%，相应的基岩地震水平动峰值加速度ah＝310 cm／s2，相应动态分布系数取2.25，地震作用效应折减系数取0.25；③死水位＋设计地震：地震加速度基准值为50年内超越概率10%，相应的基岩地震水平动峰值加速度ah＝149 cm／s2，相应动态分布系数取3.0，地震作用效应折减系数取0.25。

卡基娃面板堆石坝坝坡稳定计算的材料强度参数见表1、表2。

2.2.2 计算成果分析

按平面问题的极限平衡理论计算，分别采用瑞典圆弧法和简化毕肖普法，对各工况的坝坡稳定最小安全系数及相应临界滑弧进行计算；利用高堆石坝坝坡稳定可靠度计算的混合迭代法对坝坡进行可靠度计算。计算成果见表3，不同方法的坝坡最危险滑弧见图1至图3。在计算过程中，人为地将滑弧位置划分为坝坡滑弧与深层滑弧，此处如此划分仅为方便滑弧的搜索，对计算结果并无影响。

表2 坝坡稳定可靠度计算参数Table 2 Parameters of reliability calculation of slope stability

表3 坝坡稳定安全系数及可靠度计算结果Table 3 Calculation results of slope stability safety factor and reliability

图1 卡基娃最大剖面安全系数简化毕肖普法坝坡最危险滑弧Fig.1 Safety factors and most dangerous slip circles of dam slope calculated by simplified Bishop method considering maximum section

图2 卡基娃最大剖面安全系数瑞典圆弧法坝坡最危险滑弧Fig.2 Safety factors and most dangerous slip circles of dam slope calculated by Sweden slip circular method considering maximum section

图3 卡基娃最大剖面可靠度毕肖普法坝坡最危险滑弧Fig.3 The reliability and most dangerous slip circles of dam slope calculated by Simplified Bishop method considering maximum section

（1）从安全系数计算结果及不同方法坝坡最危险滑弧位置图可以得出如下成果。

对于瑞典圆弧法而言：①上游坝坡由于水压作用，其Fsmin最大，下游坝坡次之；下游坝坡深层滑动的Fsmin最小，但都大于规范允许值［k］＝1.2，且有较大富余，临界滑弧均为深滑弧。②正常蓄水位工况由于上游水位提高，水压对增加上游坝坡稳定性的作用更加明显，与施工工况比较，上游坝坡Fsmin增大约1倍，而下游坝坡及深层滑动的Fsmin无大的变化，且都超过规范允许值［k］＝1.3，并有较大富余；设计和校核洪水位下游坝坡及深层滑动的Fsmin与正常蓄水位工况基本相同。③从正常蓄水位＋设计地震、正常蓄水位＋校核地震、死水位＋设计地震之间的比较看出，上游坝坡的抗震稳定性主要受地震加速度和库水位的影响，地震加速度越大、库水位越低则安全系数越小；下游坝坡及深层滑动的抗震稳定性则主要受地震加速度影响。

对简化毕肖普法而言：①简化毕肖普法由于计入了条间力的影响，故其安全系数计算值大于不计条间力的瑞典圆弧法，施工工况的安全系数平均大7.1%，稳定渗流工况平均大6.1%，地震工况平均大6.2%，总体平均大6.3%，符合一般规律；②各工况上游坝坡的安全系数明显大于下游坝坡及深层滑动，与瑞典圆弧法一致，各工况、各参数组合的临界滑弧位置也与瑞典圆弧法基本相同。

（2）从可靠度计算结果可以得出如下成果：

①由于水压作用，上游坝坡的βmin最大，且βmin随水位的升高而增大；各工况下游深层滑动的βmin均大于下游坝坡的βmin，与Fsmin的分布规律一致。βmin相应的临界滑弧均为深滑弧。

②施工和稳定渗流工况上、下游坝坡及深层滑动的βmin都大于水工统标规定的目标可靠度（βT＝4.2）。地震工况，不考虑地震发生的概率时，正常蓄水位＋设计地震工况下游坝坡、正常蓄水位＋校核地震工况下游坝坡、正常蓄水位＋校核地震工况下游深层抗滑、死水位＋设计地震工况下游坝坡的βmin分别为3.119 1，2.041 7，4.149 7，3.119 1，小于允许值βT，考虑地震发生的概率后，分别为3.743 6，3.344 9，4.971 3，3.743 6，小于规范允许值。

3 结 论

通过以上分析可获得以下几点结论和建议：

（1）瑞典圆弧法和简化毕肖普法的安全系数计算结果规律一致，在给定参数下，各工况不同方法计算得到的上、下游坝坡及深层滑动的Fsmin均满足规范要求。简化毕肖普法由于计入了条间力的影响，其安全系数计算值大于不计条间力的瑞典圆弧法，总体大6.3%，符合一般规律。

（2）由于水压作用，各工况上游坝坡的安全系数明显大于下游坝坡及深层滑动。地震工况的安全系数计算结果显示，上游坝坡的抗震稳定性主要受地震加速度和库水位的影响，地震加速度越大、库水位越低则安全系数越小，下游坝坡及深层滑动的抗震稳定性则主要受地震加速度影响。

（3）上游坝坡最小安全系数对应临界滑弧的位置主要受水位影响，各工况下游坝坡及深层滑动的临界滑弧位置都比较接近，下游坝坡的临界滑弧从下游堆石体底部附近滑出，深层滑动的临界滑弧从下游围堰下游侧坡脚附近滑出。

（4）由于水压作用，上游坝坡的βmin明显大于下游坝坡及深层滑动，且βmin随水位的升高而增大，与Fsmin的规律一致。除正常蓄水位＋设计地震、正常蓄水位＋校核地震、死水位＋设计地震工况下游坝坡的βmin小于规范允许值外，其他工况均满足要求。

（5）各工况与上游坝坡βmin对应的临界滑弧的水平深度较大，滑弧出口位置较低，而与Fsmin对应的滑弧出口位置较高；与下游坝坡βmin和Fsmin对应的滑弧位置比较接近，且主要位于下游堆石体中，说明堆石体参数对可靠度对应下的滑弧影响很大。

［1］ 陈祖煜.土质边坡稳定分析［M］.北京：中国水利水电出版社，2003.（CHEN Zu-yu.Soil Slope Stability Analysis［M］.Beijing：China Water Power Press，2003.（in Chinese））

［2］ CHENG Y M.Location of Critical Failure Surface and Some Further Studies on Slope Stability Analysis［J］.Computer and Geotechnics，2003，（1）：255－267.

［3］ CHENG Y M，LI L，CHISC.Performance Studies on Six Heuristic Global Optimization Methods in the Location of Critical Slip Surface［J］.Computer and Geotechnics，2007，34（6）：462－484.

［4］ BACKER R，GARBER M.Theoretical Analysis of the Stability of Slopes［J］.Geotechnique，1978，（28）：341－395.

［5］ CHENG Y M，YIPC J.Three-Dimensional Asymmetrical Slope Stability Analysis Extension of Bishop’s，Janbu’s，and Morgenstern-Price’s Techniques［J］.Journal of Geotechnical and Geoenvironmental Engineering，2007，（11）：1544－1555.

［6］ 孙玉科，牟会宠，姚宝魁.边坡岩体稳定性分析［M］.北京：科学出版社，1988：228－233.（SUN Yu-ke，MOU Hui-chong，YAO Bao-kui.Analysis of Rock Slope Stability［M］.Beijing：Science Press，1988：228－233.（in Chinese））

［7］ 张继周，缪林昌，刘 峰.岩土参数的不确定性及其统计方法［J］.岩土力学，2008，（28）：495－499.（ZHANG Ji-zhou，MIU Lin-chang，LIU Feng.Uncertainties of Soil Properties and Its Statistical Methods［J］.Rock and Soil Mechanics，2008，（28）：495－499.（in Chinese））

［8］ 四川大学水电学院.木里河卡基娃水电站面板堆石坝非线性强度指标坝坡稳定与可靠性研究［R］.成都：四川大学水电学院，2011：9－11.（College of Water Resources and Hydropower of Sichuan University.Research on Dam Slope Stability and Reliability of Kajiwa Concrete-Face Rockfill Dam on Muli River Using Nonlinear Strength Indexes［R］.Chengdu：College of Water Resources and Hydropower of Sichuan University，2011：9－11.（in Chinese））

［9］ 吴震宇，陈建康，许唯临，等.高堆石坝非线性强度指标坝坡稳定可靠度分析方法研究及工程应用［J］.岩石力学与工程学报，2009，28（1）：131－132.（WU Zhen-yu，CHEN Jian-kang，XUWei-lin，etal.Research on Methodology of Reliability Analysis of High Rockfill Dam Slope Stability Using Nonlinear Strength Indexes and Its Engineering Application［J］.Rock Mechanics and Engineering，2009，28（1）：131－132.（in Chinese） ）

（编辑：姜小兰）

Slope Stability and Reliability of Kajiwa Concrete-Face Rock fill Dam Using Nonlinear Strength Parameters

ZHENG Tian-zhong1，WANGWan-qian2，LIXiao-xiao2，LUOWen-guang2，CHEN Jian-kang2
（1.The Seawall River Management Office ofWenzhou，Wenzhou 325000，China；2.College ofWater Resource and Hydropower，Sichuan University，Chengdu 610065，China）

Large-scale concrete-face rockfill dams are facingwith technological challenges caused by geological condition，high seismic intensity，and large dam height.We adopted the limit equilibrium theory and reliability theory to calculate the dam slope stability of Kajiwa concrete-face high rockfill dam.We analyzed the slope stability and reliability considering nonlinear strength parameters，and investigated the influence of technical indexes and safety factors on the slope stability.Compared with the limit equilibrium method，the reliability-theory-based method employed to design dam slope could quantify the safety margin，and thereby is contributive for the optimal design of high rockfill dam slope.It’s of practical significance for cost reduction and environmental protection.

limit equilibrium method；reliability；dam slope stability；Kajiwa concrete-face rockfill dam

TV331

A

1001－5485（2012）06－0068－06

2011－10－18

郑田中（1981－），女，浙江平阳人，工程师，主要从事水利管理方面的研究工作，（电话）13858862175（电子信箱）alina＠wzsl.gov.cn。

王万千（1989－），男，甘肃金昌人，硕士研究生主要从事水工结构工程方面的研究工作，（电话）13666148251（电子信箱）wangwanq117＠126.com。