并行分布式算法FIR 滤波器的FPGA 实现
王一海 ,俞筱楠,姜志鹏
(1.东南大学软件学院,南京 210096;2.南京工程学院康尼学院,南京 211167;3.金陵科技学院信息技术学院,南京 211169)
数字滤波器用于在数字信号处理中对输入信号做滤波处理。从实现方法来划分,可以分为FIR 滤波器和IIR 滤波器[1]。FIR 滤波器容易实现线性相位,且其单位冲激响应为有限长,使得系统总是稳定的[2]。因此FIR 滤波器在通信、图像处理等领域得到了广泛应用[3-4]。
设FIR 滤波器的阶数为N,则其数学表达式为

在实现FIR 滤波器的众多方法中,由于FPGA的独特硬件运行特点,采用FPGA 实现FIR 滤波器具有速度更快的优势。但是由于FIR 系统只有零点,只有阶数较高时才能取得所需的滤波效果[5],因此在FPGA 实现过程中将消耗大量的硬件资源。此时,采用分布式算法实现FIR 滤波器既能保证运算速度,又能大量节省片内资源。
1 分布式算法原理
分布式算法是一项重要的FPGA 技术,这种算法使得一般的乘积和计算在FPGA 实施过程中不再需要通用乘法器。分布式算法的基本思想[6]是对于乘积运算
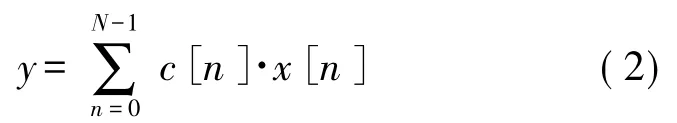
其中c[n]为已知常数,x[n]为数字变量。若x[n]为用B+1 位表达的整型无符号变量,则

其中xb[n]为x 中第b 位,取值为0或1。将上式代入式(2),可知
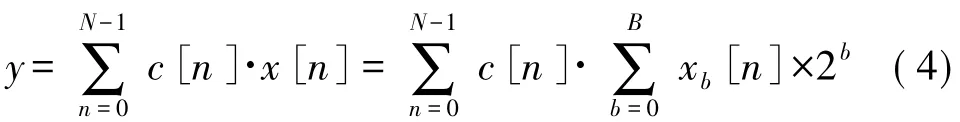
对上式稍作变换可得


当把x[n]看作由B 位有符号数表示的变量时,上式需稍加变动,根据补码的计算原理有
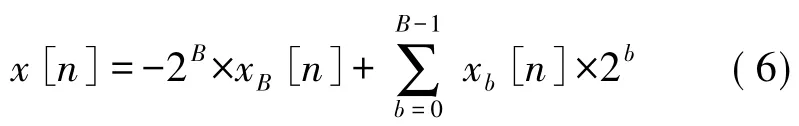
将式(6)代入式(2)中,可得

由式(7)可知,运用DA 算法实现有符合运算时,各个变量最高位与常数c[n]之间的乘加和应取负号后再参与后续运算。
基本DA 算法实现框图如图1所示。从图1 可以看出,N个变量的各位依次顺序作为地址送往LUT,LUT 从高位开始依次取出预先计算的结果进行累加求和。其中根据最高位B 位的组合获得的计算结果加负号后参与后续累加操作。
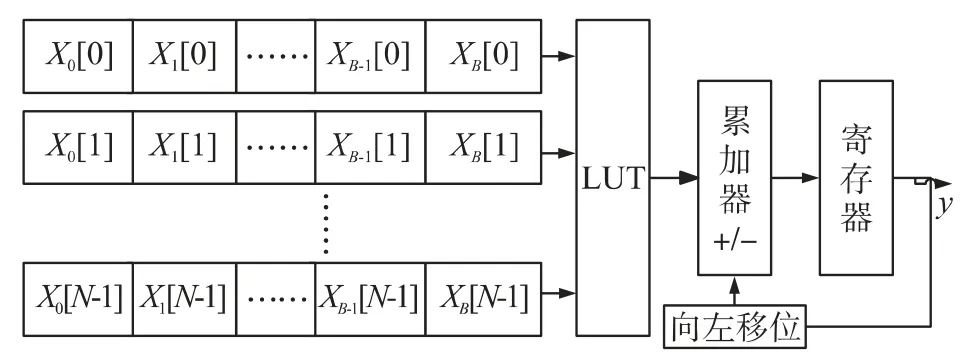
图1 基本DA 算法实现框图
使用DA 算法实现FIR 滤波器时,只要将常数c[n]看作是FIR 滤波器的各级系数,而将变量x[n]看作是输入的待滤波数据即可。
2 并行DA 算法原理
图1所示的DA 基本算法框图存在两个不足。一是对于N 阶FIR 滤波器,需要2N个存储单元。如N=32 时,将需要232个存储单元,这对FPGA 来说是一个巨大的资源消耗,有的FPGA 芯片甚至无法提供这种容量的存储单元。二是由于各个变量按位组合后访问LUT,这就使得在变量的位数较大时,从输入到结果产生有较大的延迟。
解决以上问题的办法之一[7-10]是,将原来的一个查找表分成若干小的查找表。设N=LM,即将N阶FIR 滤波器分解为L 级M 阶FIR 滤波器,则对式(7)作变换,可得

当将原表分为L=8个小表时,每个小查找表的容量为24=16个单元,8个小查找表的总容量减少为128个单元。
图2 给出了32 阶FIR 滤波器的原232单元的查找表分割为8个16 单元的查找表M1~M8,各查找表的输出依次相加,最后获得以实现分布式算法的实现框图。
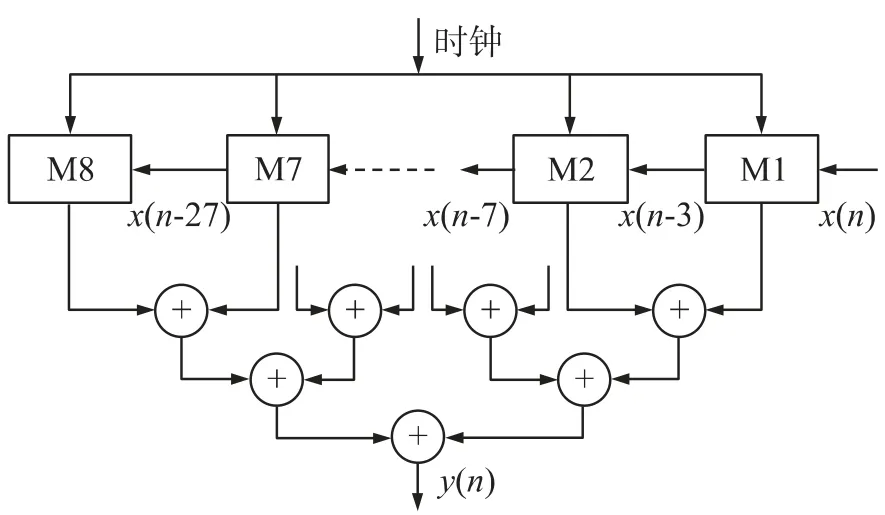
图2 32 阶FIR 滤波器分解后实现框图
图2 中的8 级查找表M1~M7模块均采用了并行结构,以第1 级查找表为例,其结构框图如图3所示。
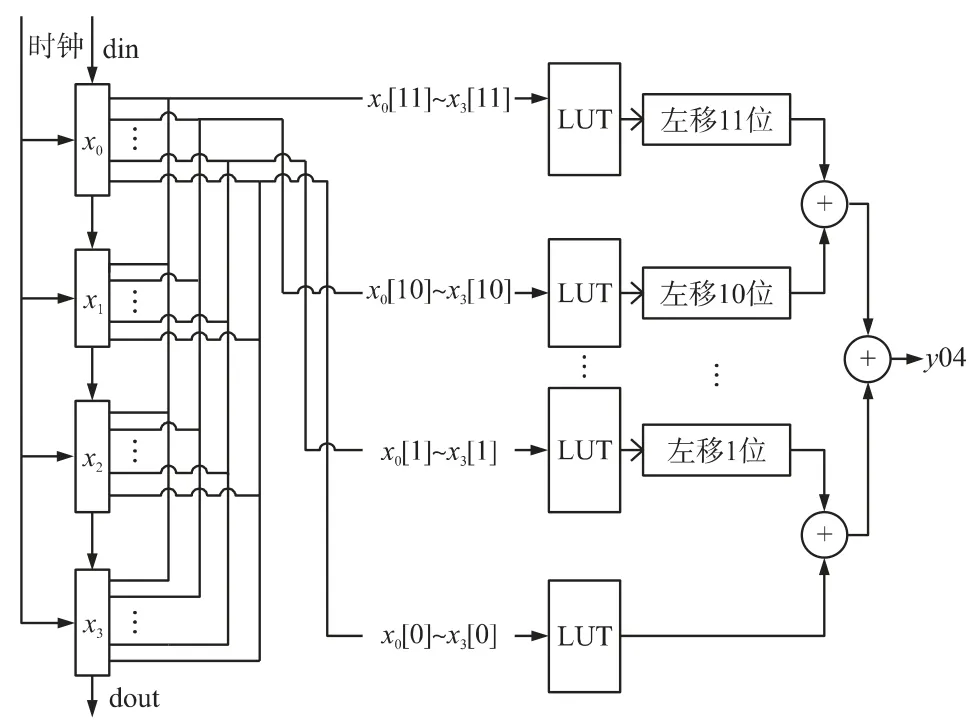
图3 图2 中M1~M8 的内部结构示意图
图3 中的每个采样值设为12 bit 补码,din为前续电路得到的新采样值,随着时钟的驱动,新采样值源源不断地进入滤波器进行滤波。图中可以看到,各个变量的最高位作为符号位,与各级系数乘加后的结果首先加负号后才参与到后续的运算中。
3 并行DA 算法的FPGA 实现
考虑到工程实际情况,本文以32 阶FIR 滤波器为例,针对以12 bit 表达的补码变量进行FIR 滤波运算。
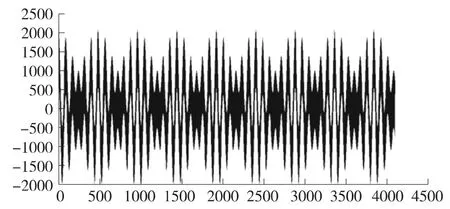
图4 MATLAB 中获得的待滤波时域波形
3.1 设计指标
本文采用MATLAB 的滤波器设计分析工具FDATOOL 设计了一个采样率为30 kHz、通带带宽为8 kHz 的汉宁窗32 阶的FIR 滤波器。用于仿真的数据由2.5 kHz、3 kHz 两个低频信号和60 kHz 的高频信号叠加产生。其波形如图4所示。在MATLAB 对取得的32 阶系数进行验证,验证结果表明能够有效滤波,如图5所示。
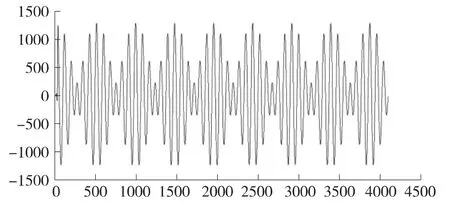
图5 FDATOOL 获得FIR 系数的滤波效果
3.2 FPGA 仿真结果
将MATLAB 产生的待仿真数据量化为12 bit 的补码数据后送至FPGA 芯片仿真测试。芯片采用ALTERA 公司的CYCLONEⅡ系列的EP2C8Q208C7。其仿真结果如图6所示。从图中可以看出FPGA 的运行结果与MATLAB 结果相符。

图6 QuartusⅡ中仿真结果
4 结论
本文对DA 算法及其并行化改进算法进行了研究,编写了VHDL 代码,在QUARTUSⅡ软件中仿真通过。设计中利用FIR 滤波器的线性特性,将32 阶FIR 滤波器分解为8个4 阶FIR 滤波器,大大减少了LUT 的容量。仿真结果表示从输入到输出的时延仅为40ns,远高于基本DA 算法串行运算时的速度。本文研究的FIR 滤波器实现方法具有较高的实用价值。
[1]胡广书.数字信号处理理论、算法与实现[M].清华大学出版社,2003.
[2]吴镇扬.数字信号处理[M].高等教育出版社,2004.
[3]叶和忠.软件无线电中数字上下变频器的研究与开发[D].桂林电子科技大学,2010.
[4]李金明.数字FIR 滤波器在监控系统中图像信号处理方面的应用[D].兰州理工大学,2006.
[5]戴曜泽,王春雷,朱智强.基于FPGA 高阶FIR 滤波器的实现[J].现代电子技术,2012,35(8):110-113.
[6]姜宇柏,游思晴.软件无线电原理与工程应用[M].机械工业出版社,2007.
[7]周大鹏,何光普,陈莉明.基于改进DA 算法和流水线技术的FIR 数字滤波器设计[J].煤炭技术,2012,32(3):33-35.
[8]赵岚,毕卫红,刘丰.基于FPGA 的分布式算法FIR 滤波器设计[J].电子测量技术,2007,30(7):101-104.
[9]于亚萍,刘源,卫勇.利用改进DA 算法FIR 滤波器的仿真与实现[J].计算机工程与应用,2011,47(27):77-79,118.
[10]杨鸿武,丁朋程,王全州.基于FPGA 的高速全并行FIR 滤波器的设计[J].西北师范大学学报(自然科学版),2012,48(1):48-51.
[11]金燕,王明,葛远香.基于FPGA 的抗混叠FIR 数字滤波器的设计与实现[J].浙江工业大学学报,2010,38(2):192-196.
[12]刘彬彬,林伟.基于Matlab和FPGA 的CIC 滤波器的设计[J].电子器件,2010,33(2):231-234.

