基于灰色系统理论的我国木质产品产量预测模型的建立1)

黄文学 刘 凌

(习水县林业局，习水，564600) (云南省林业科学院)

闫争亮 季 梅 泽桑梓

(国家林业局云南珍稀濒特森林植物保护和繁育重点实验室/云南省森林植物培育与开发利用重点实验室) (云南省林业科学院)

随着对外贸易和国内经济建设的发展，我国木质产品产量在逐年上升［1-2］，但影响木质产品产量的因素很多，包括我国对林业生产的投入、森林环境的逐步改善、国内经济建设和国外市场的拓展等等，其中一些影响因素是确定的，有一些是不确定的，是一个“灰色系统”。为明确我国的主要木质产品产量的增长规律，笔者利用灰色系统理论构建了主要木质产品产量的预测模型，可以通过模型进行预测，了解未来我国木质产品产量的增长情况，合理调节木质产品产量和需求量的关系。

灰色预测法是一种对含有不确定因素的系统进行预测的方法［3］。灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列;然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况［4］。

1 材料与方法

1.1 数据及来源

选择了我国2001—2009年的木材主要产品的产量，包括木材、竹材、锯材和人造板作为分析数据(见表1)，样本数据来源于中国林业统计年鉴2005、2010［5-6］。

表1 我国2001—2009年木材主要产品产量

1.2 灰色系统预测模型

实验采用灰色GM(1，1)预测模型对我国木质产品产量进行预测。灰色GM(1，1)预测模型为GM模型，Gm(1，1)表示1阶的、1个变量的微分方程模型。灰色GM(1，1)预测模型的计算利用Matlab7.0完成。

GM(1，1)预测模型的建立［7］：

利用原始数据序列 X(0)={X(0)(i)，i=1，2，…，n}(X(0)为非负序列)进行一次累加生成处理，生成新系列X(1)。

其中：

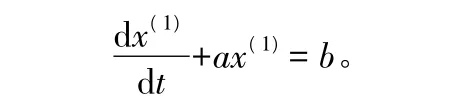
式中：a为发展灰数;b为内生控制灰数，其中a的有效区间为(-2.2)。

由于GM(1，1)模型得到的是一次累加量，k∈{n+1，n+2，…}时刻的预测值，必须将 GM(1，1)模型所得数据 ^X(1)(k+1)(或 ^X(1)(k))经过逆生成，即累减生成(I-AGO)还原为 ^X(0)(k+1)(或|^X|(0)(k))才能用。

最终得到：

对此生成序列，GM(1，1)模型白化形式的微分方程为(即 GM(1，1)模型)：

为了判别模型的优劣，可用残差检验(P)、关联度(R)、后验差检验(C)等方进行检验，具体步骤参考文献［8］，检验标准一般按着表2进行划分，关联度大于0.6时，所建模型的检验结果可以达到为满意效果［9］。

表2 精度检验等级

2 结果与分析

2.1 木材产量的灰色系统预测

利用matlab软件对我国2001—2009年木材产品产量的灰色系统分析，预测值和残差检验结果见表3，并建立了GM(1，1)模型：

预测模型为：

该模型后验差检验 C=0.23＜0.35，残差检验 P=1＞0.95，关联度 R=0.65，表明后验差和关联度检验结果为满意，预测模型精度高，等级为一级水平，可直接用于预测我国在未来年份的木材产品产量。

2.2 竹材产量的灰色系统预测

利用matlab软件对我国2001—2009年竹材产量的灰色系统分析，预测值和残差检验结果见表4，并建立了GM(1，1)模型：

预测模型为：

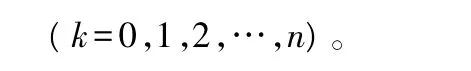
该模型后验差检验 C=0.23＜0.35，残差检验 P=1＞0.95，关联度 R=0.61，表明后验差和关联度检验结果为满意，预测模型精度高，等级为一级水平，可直接用于预测我国在未来年份的竹材产量。

表3 我国2001—2009年木材产量的预测值和残差检验结果

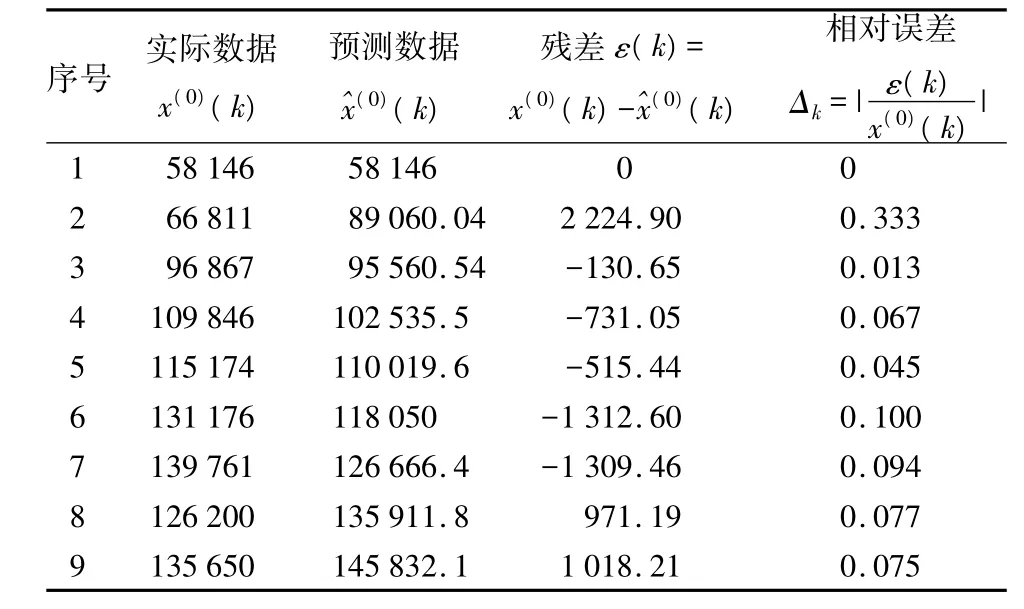
表4 我国2001—2009年竹材产量的预测值和残差检验结果

2.3 锯材产量的灰色系统预测

利用matlab软件对我国2001—2009年锯材产量的灰色系统分析，预测值和残差检验结果见表5，并建立了GM(1，1)模型：

预测模型为：

该模型后验差检验 C=0.14＜0.35，残差检验 P=1＞0.95，关联度 R=0.63，表明后验差和关联度检验结果为满意，预测模型精度高，等级为一级水平，可直接用于预测我国在未来年份的锯材产量。

2.4 人造板产量的灰色系统预测

利用matlab软件对我国2001—2009年人造板产量的灰色系统分析，预测值和残差检验结果见表6，并建立了 GM(1，1)模型：

预测模型为：

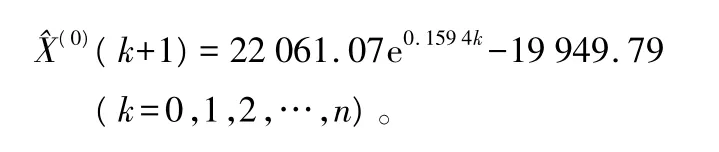
该模型后验差检验 C=0.09＜0.35，残差检验 P=1＞0.95，关联度 R=0.67，表明后验差和关联度检验结果为满意，预测模型精度高，等级为一级水平，可直接用于预测我国在未来年份的人造板产量。

表5 我国2001—2009年锯材产量的预测值和残差检验结果

表6 我国2001—2009年人造板产量的预测值和残差检验结果

3 结论

实验针对我国近年来主要木质产品产量的现状，利用灰色系统建立了GM(1，1)预测模型，来预测我国木质产品的产量的发展趋势。从以上模型的预测值来看，GM(1，1)预测模型预测精度较高，相对误差较小，拟合效果非常好，能很好地对木材、竹材、锯材和人造板等木质产品的产量进行预测。

用预测模型进行观测，可以计算出2010年—2012年木材产品产量分别约为8 565万、9 272万、10 037万m3;竹材产量分别约为156 480万、167 900万、180 150 万根;锯材产量约为 4 103.8 万、4 822.2万、5 666.3万m3;人造板产量分别约为13 644万、16 001万、18 766 万 m3。

目前，我国经济林产品年产量达已经达到6 880万t，居世界第1位。随着林业产业工业化进程的加快，林产品的需求量也会随着之增加。预测结果也能较好地指导我国的林业部门通过森林环境、国内经济建设和国外市场的拓展对林产品产量的要求和需求来调整林业生产的投入。

因为灰色系统GM(1，1)模型所需实际样本数据少，对于短期内的产量能够很好地做出预测，但预测过程中系统外在影响因素经常会发生突然波动，进而会造成模型内部参数突变，导致预测精度降低。因此，在下一步的实验中，应考虑各个因素的变化规律，利用合理的修正方法对预测模型进行修正，使预测模型更准确的反应木质产品的产量的变化规律。

［1］张颖.我国林产品进出口贸易及其影响因素分析［D］.天津：天津财经大学，2010.

［2］朱光前.中国进口木材及林产品的态势及走向［J］.木材工业，2004，18(2)：1-7.

［3］林则宏，宋凯.利用灰色预测法对科技成果转化率的预测［J］.沈阳工业学院学报，2002(2)：121-124.

［4］宋秀英.基于MATLAB的灰色预测GM(1，1)模型在经济分析中的应用［J］.数学学习与研究，2011(11)：93-95.

［5］国家林业局.中国林业统计年鉴2004［M］.北京：中国林业出版社，2005.

［6］国家林业局.中国林业统计年鉴2010［M］.北京：中国林业出版社，2011.

［7］顾晓辉，王晓鸣，赵有守.基于灰色系统预测直升机航迹的研究［J］.航空学报，2001，22(6)：559-562.

［8］洪求枝，高明成，夏莹娇.灰色系统预测方法在我国私人汽车拥有量预测中的应用［J］.长江大学学报：自然科学版，2008，5(1)：132-134.

［9］徐国祥.统计预测和决策［M］.3版.上海：上海财经大学出版社，2008.