应用主曲线确定沥青混合料的粘弹性参数

滕旭秋，李晓钟

（甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2.兰州交通大学，甘肃 兰州 730070）

0 引言

沥青混合料的力学性质与温度及荷载作用频率密切相关。国外在进行路面结构设计时常采用动模量作为设计参数，而我国路面结构设计参数常采用静态模量。二者不仅在数值上相差很大，而且动模量的采用更能有效地反映荷载、环境及路面结构之间的相互作用。所谓主曲线(master curve)是粘弹性材料在不同温度和荷载作用频率下得到的力学性质按照一定的法则通过平移后形成的一条在参考温度下的光滑曲线。常见的主曲线主要包括动模量主曲线及相位角主曲线，并且可通过对两条主曲线上对应数值的计算确定沥青混合料的粘弹性参数[1]。

由于试验仪器的限制，恒应变松弛试验难于实现，而恒应力蠕变试验虽然较易实现，但在试验中却不可能得到一个真正的矩形荷载，任何仪器都需要一定的时间才能使施加的荷载达到目标值，而确定材料参数时混合料初始受力状态对参数的确定影响很大，这不可避免的导致测量得到的参数存在一定的误差。而在试验中通过频率扫描试验测定沥青混合料的动态模量及相位角则比较容易实现，并且其试验精度能得到较好的控制。

1 试验设计

1.1 试件成型及数据获取

试验所用沥青混合料包括AC-13、AC-20及沥青稳定碎石LSAM-30三种。AC-13、AC-20所用沥青为浙江兰亭SBS改性沥青，LSAM-30所用沥青为滨州70＃沥青，两种沥青的技术性能指标检测均符合规范相应的规定。AC-13、AC-20级配取用规范推荐级配的中值，LSAM-30级配采用贝雷法设计。AC-13的设计空隙率为4.2%，最佳油石比为5.1%；AC-20的设计空隙率为4.5%，最佳油石比为4.3%；LSAM-30的设计空隙率为4.0%，最佳油石比为3.4%。通过马歇尔试验测定的各项指标满足规范的要求。

按上述确定的沥青混合料配比成型300 mm×300 mm×100 mm的车辙板后，利用钻芯机钻取直径为100mm的圆柱体芯样，由于测量应力及应变的MTS设备采集数据时对试件的平整度及垂直度都有一定的要求，因此在钻芯过程中要特别注意车辙板及钻芯机都应牢固地立于某一位置，不应发生扭转或移动。

试验采用应力控制方式，对试件施加正弦荷载，通过液压饲服系统MTS材料试验机进行相应的动态荷载及相应应变的采集，数据的采集间隔时间随频率的增加而减小，采集的数据为后期确定动模量及相位角服务。试验参考文献[2]的试验方法进行。试验温度取为四个温度，分别为-10℃、15℃、25℃及35℃；荷载作用频率取为 1 Hz、4 Hz、8 Hz和 12 Hz。

测得相应的应力及应变后，可采用下式计算对应的动模量及相位角。

A—试件的面积；

σ0—应力。

应变的计算可参考下式进行：

GL—卡规的标准长度；

ε0—应变。

则动态模量的计算公式为：

在每个荷载作用频率下的相位差可用下式计算：

式中：ti—每个荷载作用周期内应变滞后于应变的时间（Sec）；

tp—一个应力循环的平均时间（Sec）。

通过以上计算公式可以确定不同温度、不同频率荷载作用下的动模量及相位角。

1.2 试验结果整理

整理试验数据，获得的三种沥青混合料的动模量见图1～图3。

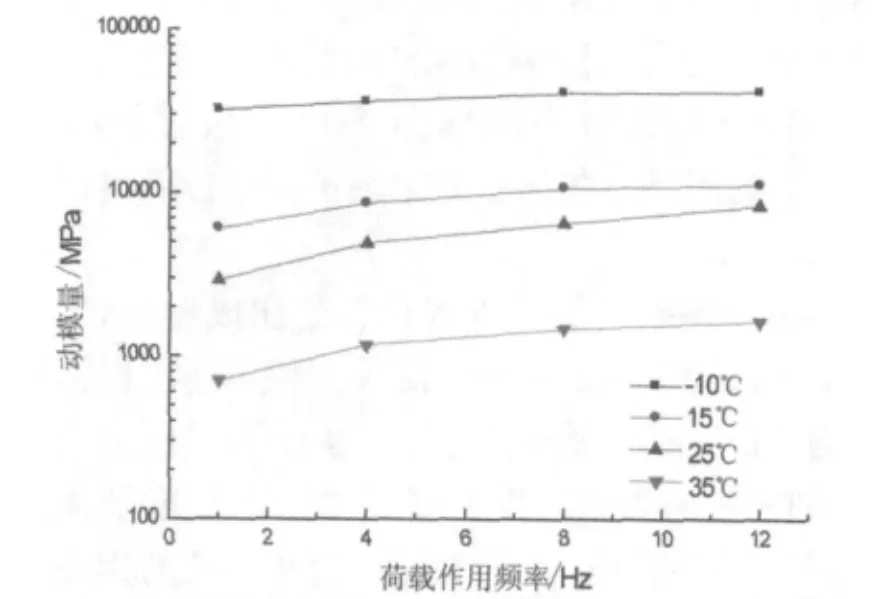
图1 AC-13动模量结果

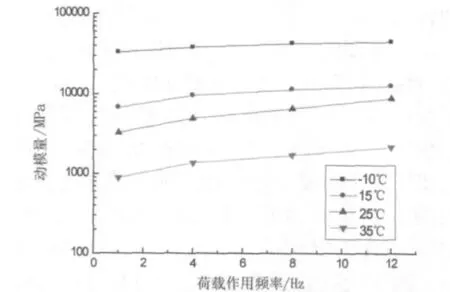
图2 AC-20动模量结果

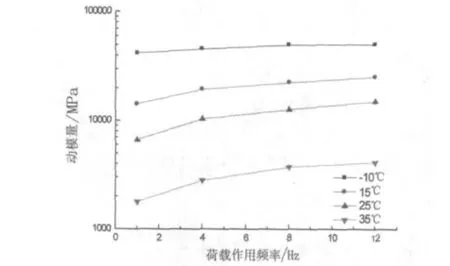
图3 LSAM-30动模量结果

由图1～图3可以看出，由于沥青为粘弹性材料，三种沥青混合料的动模量值均随着温度的升高而减低，随着荷载作用频率的增加动模量值随之增大。但是当温度较低时(-10℃)时，沥青混合料的粘弹性特征减弱，而其弹性特征变得较为明显，在图中表现为-10℃的动模量曲线值基本为一平直的直线，基本不随荷载作用频率的变化而变化。

三种沥青混合料的相位角主曲线见图4～图6。

图5 AC-20相位角结果

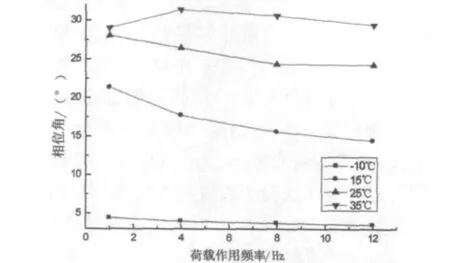
图6 LSAM-30相位角结果

从图4～图6可以看出，随着温度的增加，相位角逐渐增大，随着荷载作用频率的增加，对应的相位角则降低，这与粘弹性材料的性能一致[3]。而值得注意的一点是，三种混合料在35℃时，荷载作用频率为1 Hz时的相位角均小于荷载作用频率为4 Hz时的相位角，主要原因是在高温低频作用时，沥青胶结料硬度降低，矿料骨架的作用大于沥青胶结料的作用，因为矿料是弹性材料,相位角为零，所以沥青混合料的相位角此时会下降。

2 动模量、相位角主曲线的确定

本文利用前述在不同温度、不同频率下得到的沥青混合料的动态模量，根据时间～温度置换原理，确定沥青混合料的动态模量主曲线。参考文献[4]推荐的动态模量拟合函数（Sigmoidal函数）确定的动模量拟合函数见下式所示。

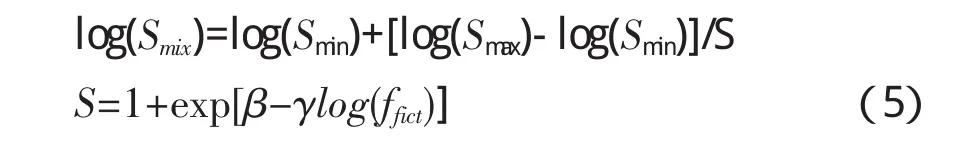
式中：Smix—混合料刚度（MPa）；

Smin—混合料最小刚度（MPa）；

Smax—混合料最大刚度（MPa）；

ffict—缩减频率（Hz）；

β，γ—形状参数。

在确定动模量主曲线之前应首先确定缩减频率ffict，其计算公式为：

式中：αT—温度转化因子；

f—荷载作用频率（Hz）。

本研究中，αT的确定采用WLF法，其计算公式为：

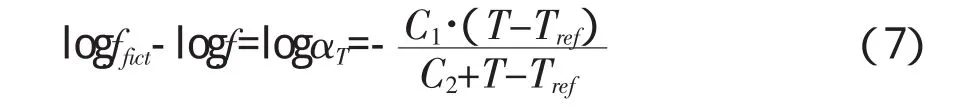
式中：ffict—主曲线将被读取的频率（Hz）；

f—荷载作用频率（Hz）；

Tref—参考温度；

T—实际温度；

C1，C2—经验常数。

若将上式带入log-Sigmoidal函数，则该式共有六个待定参数，应用非线性最小二乘法确定各个待定参数。

现以35℃数据为例，确定以上三种沥青混合料在不同温度下的动模量主曲线及相位角主曲线。拟合的动模量主曲线见图7～图9。

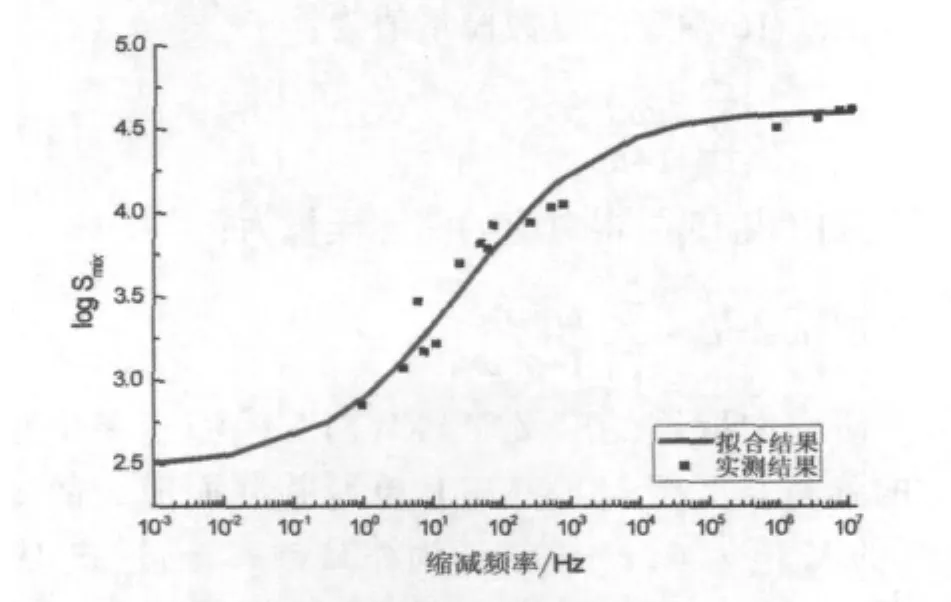
图7 AC-13动模量主曲线

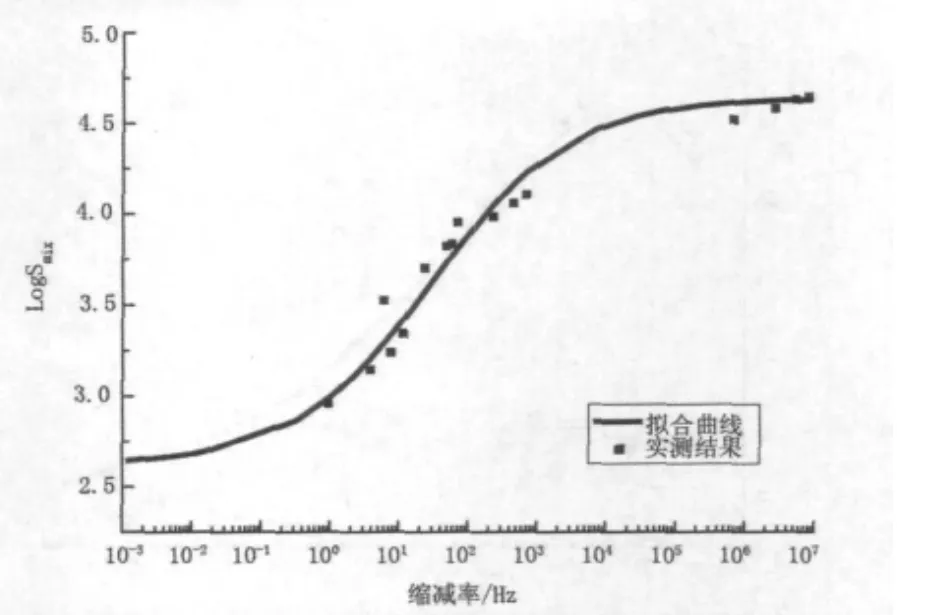
图8 AC-20动模量主曲线

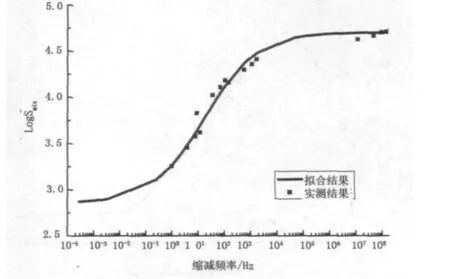
图9 LSAM-30动模量主曲线

S模型的上部逐渐接近沥青混合料的最大刚度值，其值的大小与沥青结合料的刚度值及集料的性质有关，温度较高时，集料的骨架作用对混合料模量的贡献要大于结合料的贡献，因此，在曲线的起始阶段（荷载作用频率很低相当于高温情况），动模量数值的大小与集料的级配有很大的关系。

由图7～图9可以看出，三种混合料随着集料公称粒径的增加，混合料的最小刚度值(Smin)也逐渐增加，此时数值的大小取决于集料的级配情况。

温度为35℃时，对应的相位角主曲线的温度转化因子可取用与确定动模量时相同的数值，对应的相位角主曲线见图10～图12。

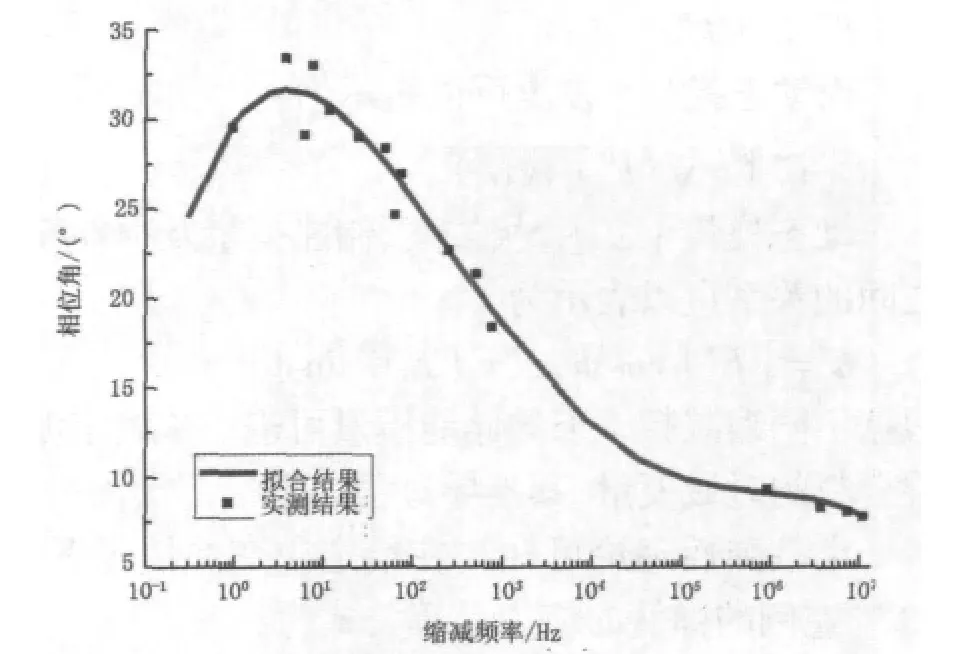
图10 AC-13相位角主曲线

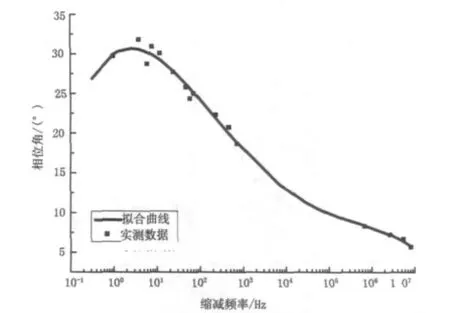
图11 AC-20相位角主曲线

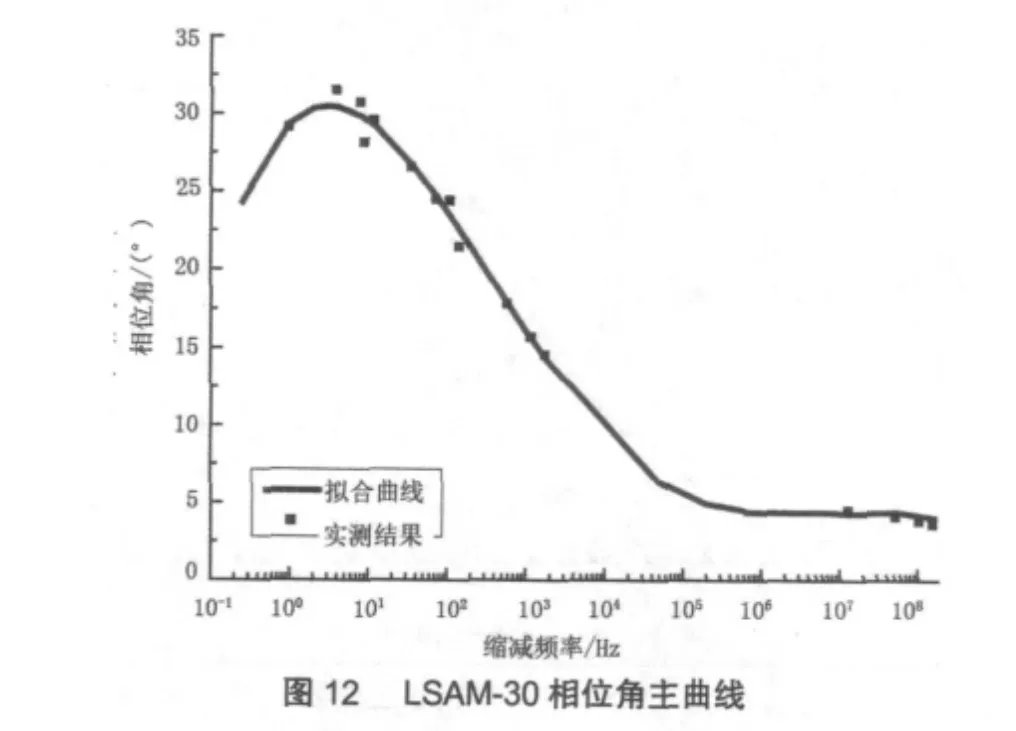
由图10～图12可以看出，三种沥青混合料的相位角都随着频率由低到高出现峰值后再逐渐减低，这符合粘弹性材料在粘弹态的力学性能变化规律[3]。当频率大于一定数值后逐渐趋于稳定，此时对应沥青混凝土的相位角数值非常小，沥青混凝土表现为弹性性质。

3 频域模量与时域模量的转化

通过频率扫描试验，可以确定粘弹性材料的复数模量E*，它是由动态模量│E*│及相位角φ组成的。复数模量E*也可用储能模量及损耗模量表示为以下形式：

而动态模量│E*│可以表示为：

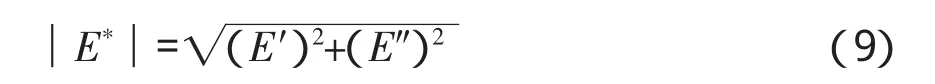
动态模量│E*│、相位角、储能模量及损耗模量之间的关系可以表示为：

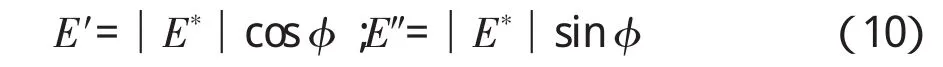
根据不同缩减频率下的储能模量可进一步确定沥青混合料的时域模量，其推导过程如下。

由粘弹性理论可知，在给定应变的情况下，图13中左侧的弹簧的应力计算公式为：

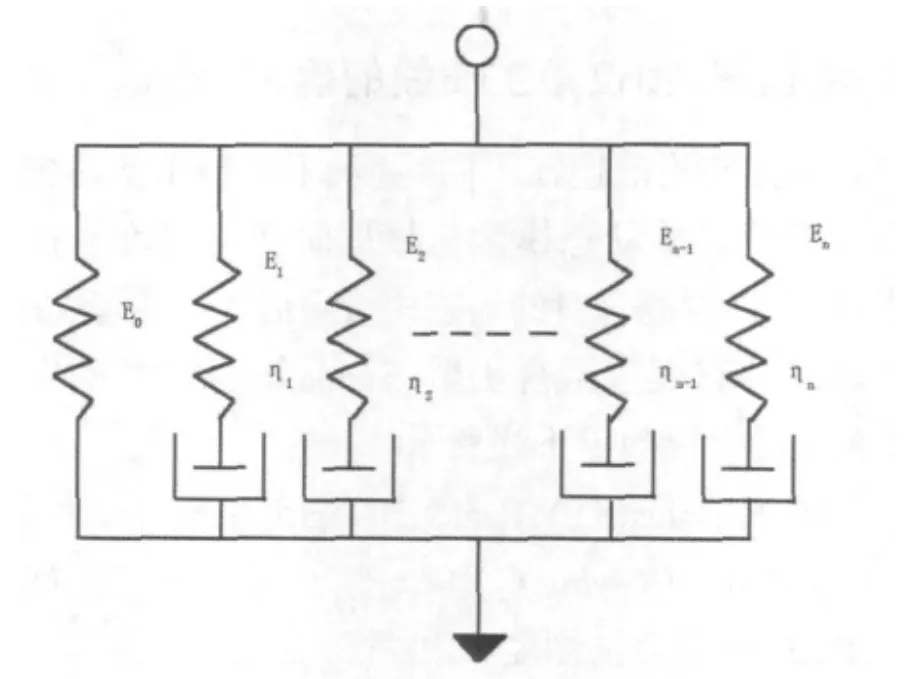
图13 修正后广义Maxwell模型

第m个Maxwell模型的本构方程的微分形式为：

对于广义Maxwell模型，其应力计算公式为：

应用积分变换理论，在零初始条件下，对式（11）及式（12）进行傅立叶变换，可分别对应得到以下表达式：

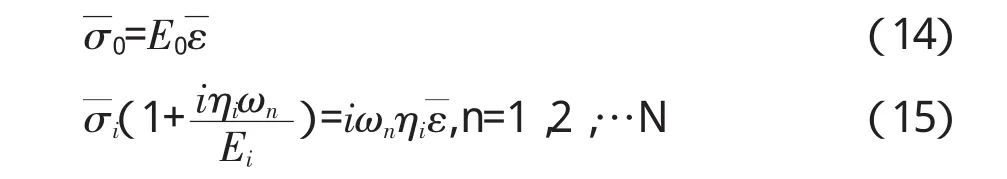
将式（14）及式（15）代入式（13）并进行傅立叶变化，可得：

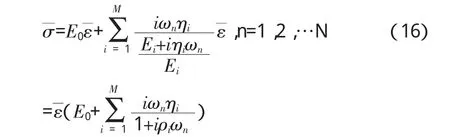
由式(16)确定的复数模量值为：

则由式(18)可得对应的储能模量为：

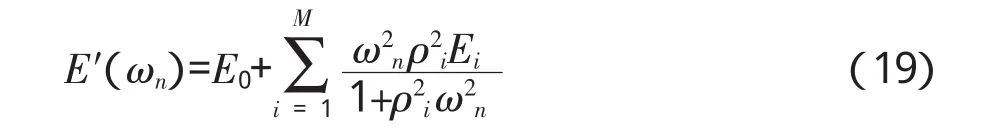
研究中取用的广义MAXWELL模型有一个独立的弹簧与四组MAXWELL单元并联而成，故式(19)的M值为4，式中的ωn为缩减频率，通过式(19)计算广义MAXWELL模型中各个弹簧及粘壶对应的粘弹性参数。其中，E0可通过下式确定[5]：

其它参数可应用拟合得到的储能模量通过非线性最小二乘法拟合获得。由式(19)可以看出，随着荷载作用频率的增加，在其它参数固定时，储能模量也逐渐增加，但当频率ωn达到一定数值时，储能模量E′（ωn）趋近于常数；若频率ωn值太小，储能模量 E′（ωn）趋近于常数 E0，鉴于此，在进行参数回归的时候取用的频率范围为0.01～1 000 Hz。确定的各粘弹性参数见表1。

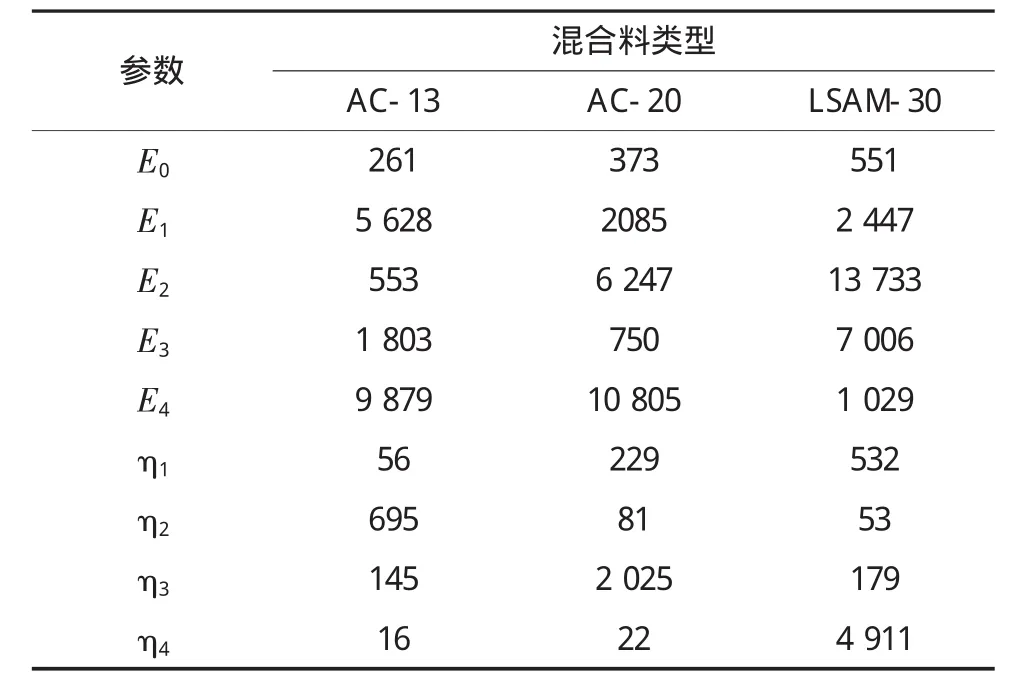
表1 35℃沥青混合料粘弹性参数

由表1的数据可以看出，E0的数值与集料的级配有一定的关系，这主要是由于在荷载作用频率很低时，沥青混合料的劲度模量主要取决于所用集料的级配，因为高温时沥青硬度降低，劲度模量主要取决于集料的骨架作用。

4 结语

本文通过频率扫描试验确定了不同温度下沥青混合料的动模量及相位角，应用粘弹性力学中的时温叠加原理将温度转换因子引入动模量主曲线的计算，并应用傅立叶变换确定了在不同荷载作用缩减频率下对应的储能模量的计算公式，最后采用最小二乘法确定了沥青混合料在一定参考温度下的粘弹性参数。由计算结果可以看出，在考虑动荷载作用时，沥青混合料的粘性效应不如静态时的粘性效应显著，这一点与路面结构的实际受力情况更加吻合。

本文研究所获得的结果均出自室内试验，其数值在路面结构设计中的应用有待于进一步研究。

[1]赵延庆,等,沥青混合料动态模量及其主曲线的确定与分析[J].公路,2006(8):163-166.

[2]NCHRP 465 APPENDIX Test method for dynamic modulus of asphalt concrete mixtures for permanent deformation[R].

[3]杨挺青.粘弹性力学[M].上海:同济大学出版社,1989.

[4]AASHTO 2002,Part2-Design Inputs,Chart2-Material Characterization[R].

[5]Sun Hgho Mun,Nonliner finite element analysis of pavements and its application to performance evaluation[D].North Carolina State University,2003.