基于二维非参数特征分析的SAR图像目标识别

刘 振,姜 晖,徐海峰

(解放军电子工程学院,合肥 230037)

1 引 言

Fisher线性鉴别分析(Fisher Linear Discriminant Analysis,FLDA)[1]通过最大化投影空间中样本的类间散度与类内散度之比来求取最优的投影方向,是一种有效的特征提取方法。但是,FLDA在用于图像的特征提取时有如下几点不足:一是FLDA只是对高斯分布最优的,即FLDA是以所有类别的样本数据服从协方差相同、均值不同的高斯分布为前提的;二是在计算散度矩阵时只考虑了类中心,不能有效地提取类的边界信息,而边界信息往往同样具有重要的鉴别信息[2];三是因为类间散度矩阵的秩最大只能为C-1(C代表总的类别个数),FLDA提取的特征个数最多只有C-1,而在高维数据及多类目标的识别任务中C-1个特征往往是不够的;四是一般图像转换成图像矢量之后的维数往往会很高,远远大于样本的个数,即会出现小样本问题。针对上述问题,文献[3-8]对FLDA进行了一定的改进。文献[3]将主成分分析(Principle Component Analysis,PCA)与FLDA相结合,缓解了FLDA的小样本问题,但使用PCA降维会丢失有用的鉴别信息。文献[4]直接在二维图像矩阵上进行FLDA的特征提取,大大降低了散度矩阵维数,缓解了小样本问题,提取的特征也不受 C-1的制约。文献[5]提出最大散度差(MaximumScatter Difference,MSD)判决分析,通过最大化投影后样本的类间与类内散度矩阵之差来求解投影方向,避免了对类内散度矩阵求逆,不会出现FLDA的小样本问题,并且大大加快了特征抽取的速度。文献[6-7]提出子类判决分析(Subclass Discriminant Analysis,SDA),先对每类目标进行子类划分,然后基于这些子类使用FLDA准则求取投影方向,SDA假设每类目标服从多模分布,可在一定程度上缓解FLDA的线性和奇异性问题,且得到的特征维数为子类总数减1(大于C-1)。文献[8]通过构造非参数形式的散度矩阵,使用非参数特征分析(Nonparametric Feature Analysis,NFA)求取投影方向,NFA能够捕捉到类的边界结构信息,并且不要求数据服从高斯分布,提取的特征也可以大于C-1。

本文在借鉴非参数特征分析(Nonparametric Feature Analysis,NFA)[8]的基础上,提出二维非参数特征分析方法(Two Dimensional Nonparametric Feature Analysis,2DNFA),大大降低了散度矩阵的维数,并根据图像矩阵的行信息和列信息的压缩方向,给出了两种形式的2DNFA。二维非参数特征分析不仅克服了FLDA只对数据高斯分布最优的缺陷,有效地提取了类的边界信息,而且降低了散度矩阵的维数,有效缓解了鉴别分析的“小样本”问题,所提取的特征个数也不再受到C-1的制约。将该方法用于对SAR图像目标的识别:在SAR图像矩阵上直接计算非参数形式的散度矩阵,进行非参数特征分析获取特征矩阵,最后基于最近邻分类器对待识别目标进行分类识别。利用美国运动和静止目标获取与识别(Moving and Stationary Target Acquisition and Recognition,MSTAR)计划录取的切片SAR数据库进行了仿真实验,结果表明两种形式的2DNFA能够以较低的特征维数获得高达98%以上的识别率,验证了本文方法有效可行。

2 非参数特征分析(NFA)

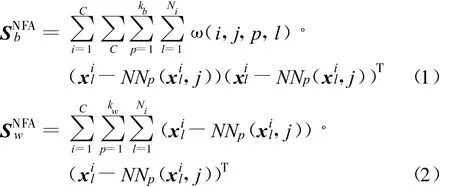
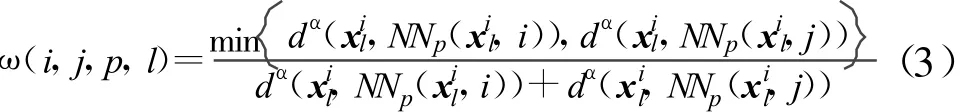
分析式(1)～(3)以及参照图1可以看出:FLDA的参数化散度矩阵的构造仅仅依靠类中心(如图1虚线箭头所示),而NFA打破了FLDA的固有限制,散度矩阵不再仅仅依赖类中心,而是由样本的近邻样本来计算,当近邻数为1时,NFA的类间散度即如图1实线箭头所示,如此构造散度矩阵更能体现数据的结构特征,提取的特征数也不再受到C-1的制约;从权值系数 ω(i,j,p,l)的式(3)定义可以看出,当样本在类边界上时ω(i,j,p,l)的值可达到或接近0.5,随着样本远离边界ω(i,j,p,l)趋向于0,权值系数 ω(i,j,p,l)使NFA更加注重对边界信息的提取[9-10]。

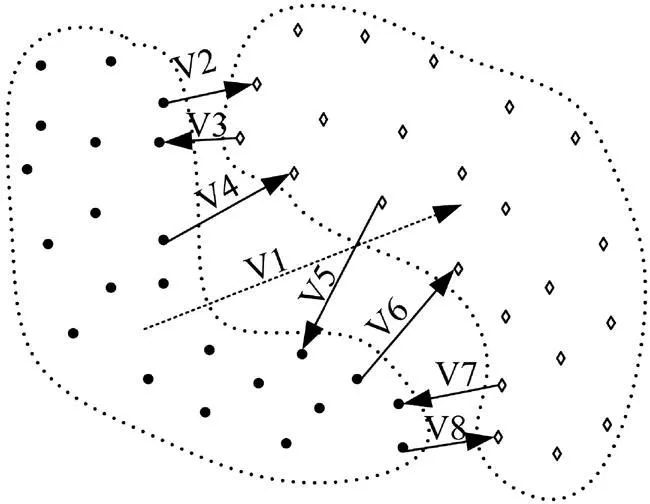
图1 NFA非参数类间散度与FLDA参数类间散度Fig.1Nonparametric between-class scatter of NFA and parametric between-class scatter of FLDA

利用式(1)和式(2)计算散度矩阵之后,最优投影方向 Wopt=[w1,w2,…,wd]∈R(m×n)×d(d (m×n))可以通过对进行特征值分解来求得,的前d个最大特征值对应的特征向量即构成Wopt。对于任意样本数据 x ∈R(m×n)×1,它在投影空间中的特征 f∈Rd×1为

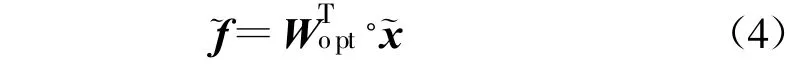
3 二维非参数特征分析

3.1 基于图像行方向的2DNFA(2DNFA)

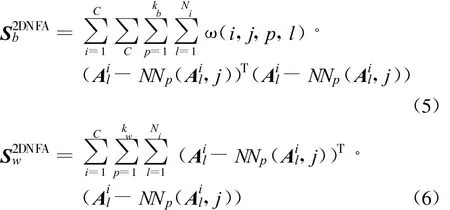
权值系数为 ω(i,j,p,l)定义如下:

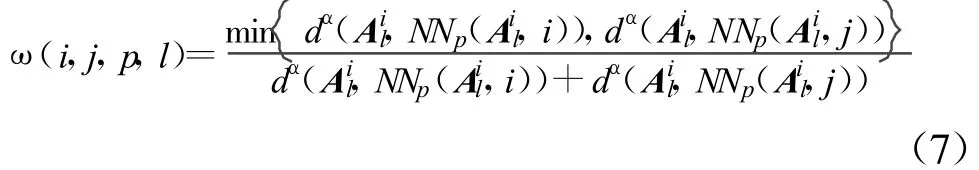
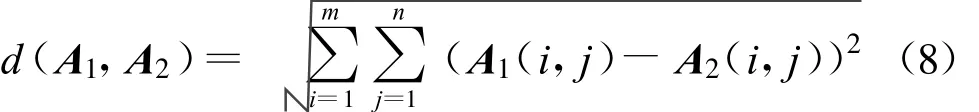
在式(6)～(9)中,A(i,j)代表矩阵A第i行j列的元素,kb、kw和α定义与第二节相同。类似于一维情况,最优投影方向 Wopt∈Rn×r(r n),即由的前r个最大特征值对应的特征向量构成。有时会出现不可逆的现象,需要对进行非奇异化处理,可使用正则化方法[11]:,μ则取为的最大特征值,In×n是n×n的单位矩阵。对于任意样本数据 A∈Rm×n,它在投影空间中的特征 F2DNFA∈Rm×r为

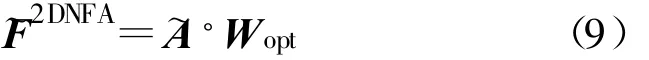
从式(5)、(6)和(9)可以看出,2DNFA方法是建立在图像矩阵行的基础上,即对行信息进行鉴别,同样,也可以从图像的列方向上进行鉴别分析。下面给出2DNFA的另一种形式——基于图像列方向的2DNFA(Alternative 2DNFA,A2DNFA)。

3.2 基于图像列方向的2DNFA(A2DNFA)

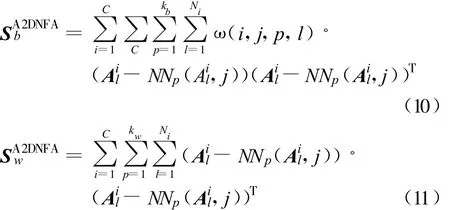
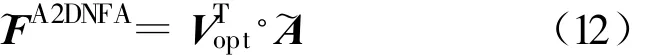
4 基于2DNFA的SAR图像目标识别

实验数据采用美国MSTAR计划录取的数据,选择 17°俯仰角 下的 BMP2-sn9563、BTR70-snc21、T72-sn132共698个样本作为训练样本集;选择俯仰角为 15°下的 BMP2-sn9563、BMP2-sn9566、BMP2-snc21、BTR70-snc71、T72-sn132、T72-sn812、T72-sns7共1 365个样本作为测试样本集,原始数据中每幅SAR图像的大小为128×128。图2给出了基于2DNFA的SAR图像目标识别主要步骤的流程图。

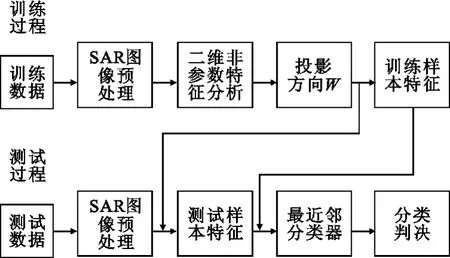
图2 基于2DNFA的SAR图像目标识别流程图Fig.2 Flow chart of SAR image target recognition based on 2DNFA

4.1 预处理

为了更好地提高识别性能,需要对图像切片进行一定的预处理[12]:通过对数变换来减小目标图像的动态范围并抑制乘性噪声,恒虚警阈值分割和形态学滤波可以进一步减小噪声的影响,基于幂变换的图像增强可以突出图像的某些信息,归一化处理消除了目标相对于SAR的距离不同造成的回波强度差异,最后对图像进行二维傅里叶变换,以保证目标的平移不变性。因傅里叶变换幅频特性具有对称性,为了压缩样本维数减小运算量,取幅频信息的一半作为特征提取的输入,这样预处理后数据的大小为128×64。

4.2 特征提取

参照3.1节和3.2节对预处理后的训练样本进行2DNFA和A2DNFA方法的特征提取,求出2DNFA的投影矩阵 Wopt∈Rn×r(r n),和A2DNFA的投影矩阵 Vopt∈Rm×l(l m)。根据式(9)和式(12)即可求出任意训练样本 Ai∈Rm×n和测试样本 T∈Rm×n在两种投影空间中的特征矩阵。

4.3 分类器设计

为了体现本文方法提取特征的有效性,使用最简单的最近邻分类器对测试目标进行识别:先计算测试样本与每个训练样本在特征空间的距离,与测试样本距离最小的训练样本的类别即为该测试样本的类别。分别对2DNFA和A2DNFA的投影空间中的距离做如下定义。

(1)基于2DNFA特征的距离定义

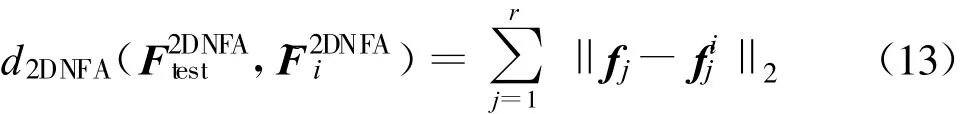
(2)基于A2DNFA特征的距离定义

5 实验仿真与分析

使用前文介绍的训练样本和测试样本进行本文方法的仿真验证,测试样本方位角信息未知,识别率取所有测试样本的平均识别率。为了简化参数的选取,预先假设计算类间散度矩阵的近邻数kb与类内散度矩阵时的近邻数kw相等,同取为k。特征维数l和r 分别取 38、34、30、26、22、18、14、10、6、2。

图3(a)和(b)显示了2DNFA和A2DNFA在特征维数不同取值下参数 α对识别率的影响,其中散度矩阵近邻个数 k=116。从图中可以看出,在r=2时,2DNFA识别率仍可以达到95%以上,A2DNFA的识别率也可以达到92%,两者在一定维数下识别率均可以达到98%以上,说明本文方法提取的特征信息具有良好的可鉴别性。从两幅图中还可以看出α对识别率的影响不是很大,所以为了降低算法的运算量,可以取 α=1。

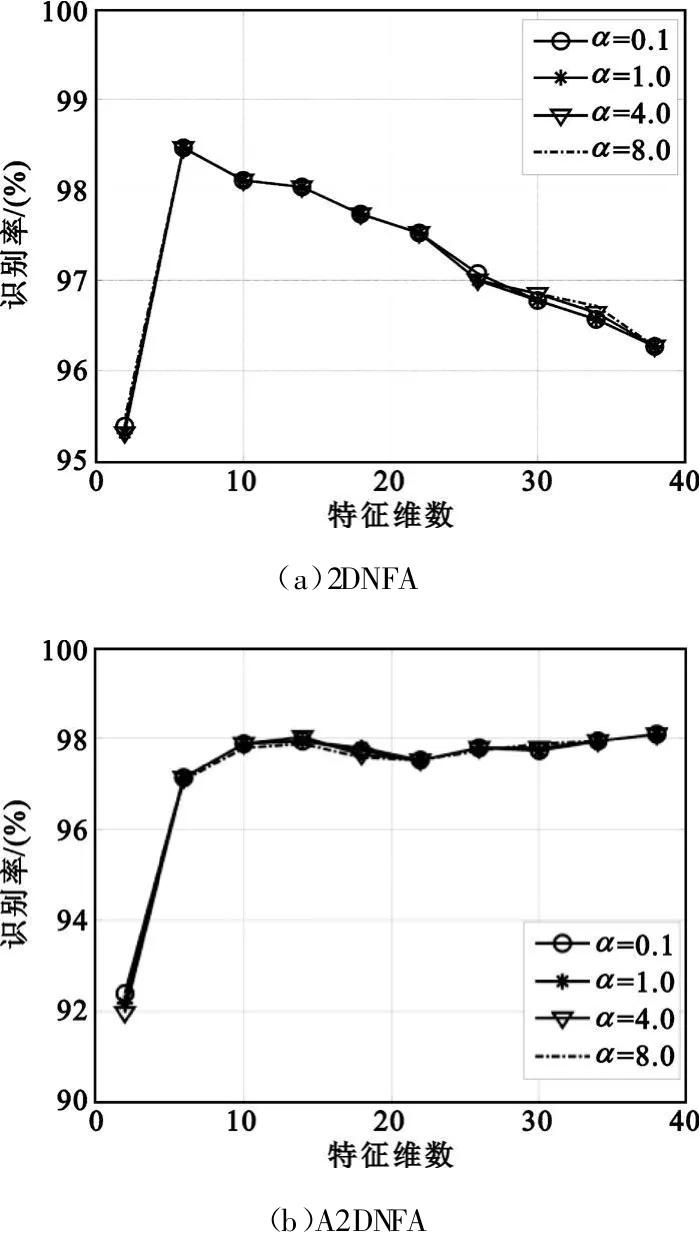
图3 2DNFA和A2DNFA在α取不同值下的识别率Fig.3 Recognition rate of 2DNFA and A2DNFA against α

图4(a)和(b)显示了2DNFA和A2DNFA在特征维数不同取值时,α=1,散度矩阵近邻个数 k对识别率的影响。从图中可以看出,本文方法对参数k也具有一定的鲁棒性,不同k值的识别率在一定特征维数下均可以达到98%以上。2DNFA在不同k值下识别率都在 95%以上;只有A2DNFA在 k=230、特征维数l=2时识别率不到85%。可见k取值并不是越大越好,一般取每类训练样本个数的一半即可[8]。

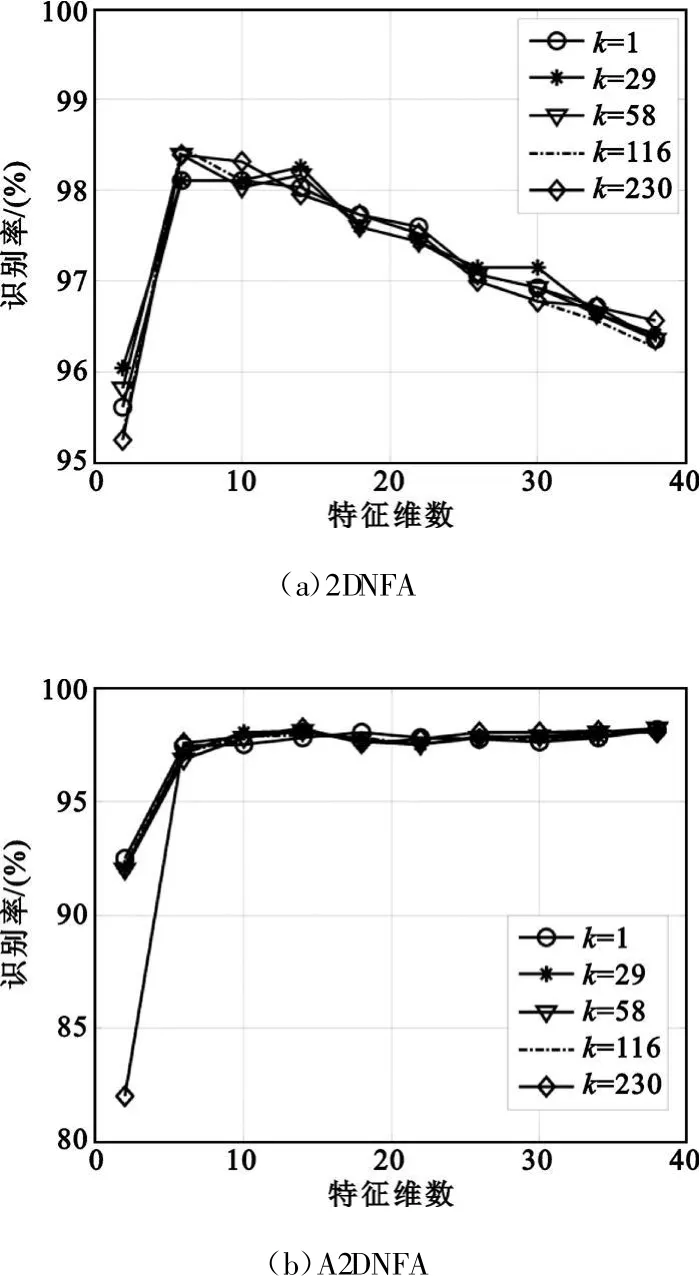
图4 2DNFA和A2DNFA在参数k不同值下的识别率Fig.4 Recognition rate of 2DNFA and A2DNFA against k

综合图3、图4可知,2DNFA和A2DNFA在较低的特征维数下即可达到识别率的峰值,因此特征维数一般选择在6～14即可。还可以看出,随着维数的进一步增大,2DNFA识别率反而出现下降的趋势,A2DNFA则在一定达到维数后识别率趋于稳定。

为了进一步验证本文方法的有效性,表1给出了本文识别结果与文献[13-15]识别结果的比较。可以看出两种形式的2DNFA获得的识别率均可高于其他方法的最优识别率,并且所需特征矩阵的维数也较小,更加验证了本文方法的有效性。

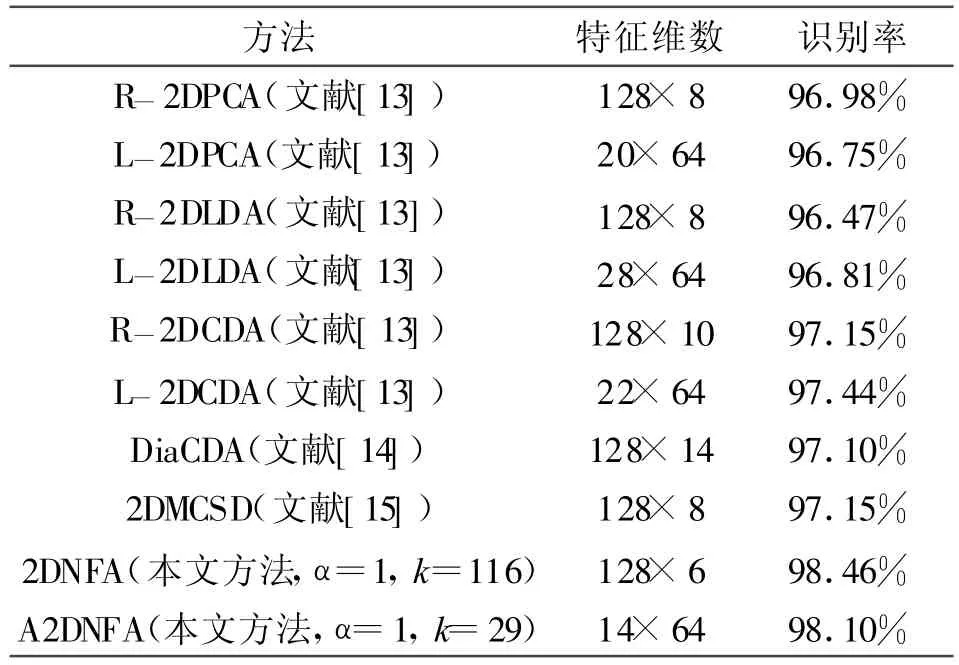
表1 不同方法的识别率比较Table 1 Comparison of recognition rate using different methods

6 结 论

本文提出了两种形式的二维非参数特征分析的特征提取方法。该算法直接在图像矩阵上提取特征,不仅能够大大地降低样本维数、减小运算复杂度,而且非参数形式的散度矩阵计算克服了传统鉴别分析的缺陷,有效利用了类的边界信息,即使在方位角未知的情况下仍然可以获得较高的识别率。通过与其他方法比较可以看出,本文方法能够以较低的特征维数达到提高识别率的目的,表明本文方法可行有效。本文仅仅是对参数α和k进行了人为的设定,如何在保证识别率的同时自适应地选择最小k值来降低训练时间是下一步需要研究的问题。

[1] Swets D L,Weng J.Using discriminant eigenfeatures for image retrieval[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(8):831-836.

[2] Fukunaga K.Statistical Pattern Recognition[M].Salt Lake City:Academic Press,1990.

[3] Swets D L,Weng J.Usingdiscriminant eigenfeatures for imageretrieval[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(8):831-836.

[4] Zheng W S,Lai J H,Li S Z.1D-LDA vs 2DLDA:when is vector based linear discriminant analysis better than matrix based[J].Pattern Recognition,2008,41(7):2156-2172.

[5] 刘永俊,陈才扣.最大散度差鉴别分析及人脸识别[J].计算机工程与应用,2006,42(34):208-210.LIU Yong-jun,CHEN Cai-kou.Maximum scatter difference discriminant analysis andface recognition[J].Computer Engineering and Applications,2006,42(34):208-210.(in Chinese)

[6] Zhu M,Martinez A M.Subclass discriminant analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelli-gence,2006,28(8):1274-1286.

[7] 张静,王国宏,杨智勇,等.基于二维子分类鉴别分析的SAR图像识别方法研究[J].电子学报,2010,38(4):797-803.ZHANG Jing,WANG Guo-hong,YANG Zhi-yong,et al.An Efficient Two-DimensionalSubclassDiscriminantAnalysisApproach for SAR Image Recognition[J].Chinese Journal of Electronics,2010,38(4):797-803.(in Chinese)

[8] Li Zhifeng,Lin Dahua,Tang Xiaoou,et al.Nonparametric Discriminant Analysis for Face Recognition[J].Pattern AnalysisMachine Intelligence,2009,31(4):755-761.

[9] Li Zhifeng,Liu Wei,YANG Zhi-yong,et al.Nonparametric Subspace Analysis for Face Recognition[C]//Proceedings of 2005 IEEE Conference on Computer Vision and Pattern Recognition.San Diego,CA,USA:IEEE,2005:961-966.

[10] Zhan Xueliang,Ma Bo.Kernel Nonparametric Discriminant Analysis[C]//Proceedings of 2011 International Conference on Electrical and ControlEngineering.Yichang:IEEE,2011:4544-4547.

[11] 胡利平.合成孔径雷达图像目标识别技术研究[D].西安:西安电子科技大学,2009.HU Li-ping.Automatic target recognition based on synthetic aperture radar images[D].Xi′an:Xidian University,2009.(in Chinese)

[12] 韩萍,吴仁彪,王兆华,等.基于KPCA准则的SAR目标特征提取与识别[J].电子与信息学报,2003,25(10):1297-1301.HAN Ping,WU Ren-biao,WANG Zhao-hua,et al.SAR Automatic Target Recognition Based on KPCA Criterion[J].Journal of Electronics and Information Technology,2003,25(10):1297-1301.(in Chinese)

[13] Hu Liping,LiuHongwei,YinKuiying,et al.Two-dimensional clustering-based discriminant analysis for synthetic aperture radar automatic target recognition[C]//Proceedings of the 8th International Symposium on Antenna,Propagation,and EM Theory.Kunming:IEEE,2008:509-513.

[14] Hu L P,Liu H W,Yin K Y,et al.Diagonal Clustering-Based Discriminant Analysis for Synthetic Aperture Radar Automatic Target Recognition[C]//Proceedings of 2009IET International Radar Conference.Guilin:IEEE,2009:1-4.

[15] Hu Liping,Liu Hongwei,Wu Shunjun.Two-Dimensional Maximum Clustering-Based Scatter Difference Discriminant Analysis for Synthetic Aperture Radar Automatic Target Recognition[C]Proceedings of the 6th International Symposium on Neural Networks.Wuhan:IEEE,2009:655-663.