双级矩阵变换器的网侧功率因数

刘晓宇 周 波 秦显慧 史明明

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京市 210016）

1 引言

双级矩阵变换器（TSMC）是由传统矩阵变换器（CMC）演化而来的新型矩阵变换器。TSMC不仅继承了CMC的正弦输入/输出电流、输入功率因数可控以及能量双向流动等优点[1]，更具有钳位电路简单、换流策略可靠和控制策略灵活等优越特性，因此TSMC比CMC更具发展潜力和应用前景[2-5]。

目前，双空间矢量（DSVPWM）控制策略被广泛使用。其中整流级的电流空间矢量控制，仅依赖于输入电压相位信息来计算整流级开关的占空比，是一种近似开环的控制，并未考虑输入电流的相位受到滤波器参数和负载的影响，使得输入电流始终超前或滞后于电网电压，无法保证单位功率因数[6-9]。但在目前的研究中，针对系统参数对网侧功率因数影响进行的研究却较少，而进一步研究系统参数对网侧功率因数角可调范围的影响更鲜见报道。本文着重分析了系统参数对网侧功率因数角的影响，研究了网侧功率因数角的可调范围，提出对于18开关双级矩阵变换器而言，由于其自身拓扑结构的限制，其网侧功率因数角有一定的可调范围，且此范围受到系统参数的影响。

为解决网侧功率因数不为1这一问题，现有的研究大多采用固定角度补偿法，文献[9,10]根据系统参数通过计算得到网侧功率因数角进行补偿。此方法简单、易实现，但当系统参数发生变化时需要重新计算补偿角，不能实现动态补偿。文献[8]提出了一种基于dq坐标系的网侧无功控制方法，但此方法计算量较大，控制较复杂[9]。本文给出了一种功率因数角的闭环控制方法，并通过实验验证该控制方法的可行性，解决了目前网侧功率因数无法实现动态补偿的问题，使网侧功率因数在系统参数变化时仍然保持为单位功率因数，实现了网侧功率因数角的闭环控制，有效提高了电能质量。

2 TSMC结构及其数学模型

TSMC主电路拓扑结构如图1所示，USA、USB、USC为三相对称电压源。为减小高频谐波对电网的污染，TSMC输入侧必须装设输入滤波器，本文中输入滤波器采用带阻尼电阻的 LC型滤波器，以提高系统稳定性，Rf、Lf、Cf分别为阻尼电阻、滤波电感和滤波电容[11-13]。TSMC整流级采用共射级串联的 IGBT器件构成双向开关，逆变级为传统的三相全桥逆变器结构，RL、LL为负载电阻和电感。文献[8,10]均推导了图1所示的TSMC的数学模型。

设三相电源电压为

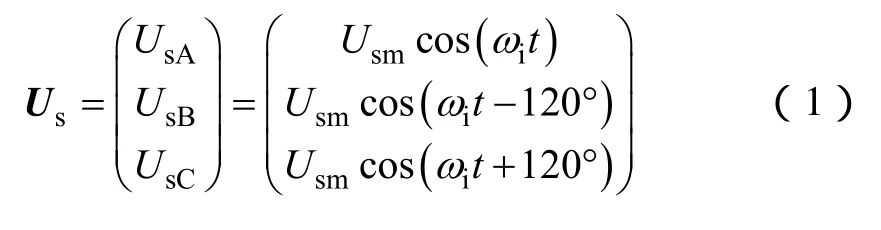
式中，Usm为电源相电压幅值；ωi为电源电压角频率。

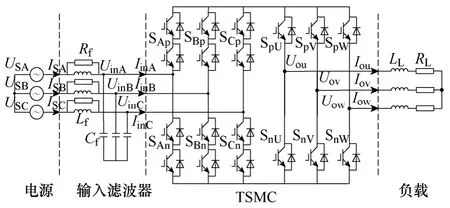
图1 双级矩阵变换器电路拓扑图Fig.1 Topology of TSMC

将网侧电流、TSMC输入电压和输出电流作为状态变量，可得TSMC主电路整体的状态空间表达式为

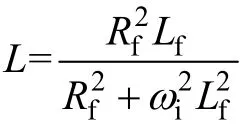
3 功率因数角及其可调范围与系统参数的关系分析

3.1 功率因数角

稳态工作时式（2）中一阶导数项为零，可以得到系统稳态时网侧输入电压、电流、TSMC侧输入电压、电流以及输出电流的解析表达式

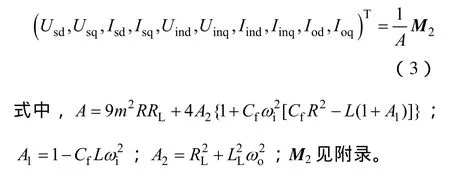
根据式（3）即可得到网侧功率因数角φsi为

式中，φi为输入功率因数设置角；m为调制系数。

TSMC输入侧功率因数角iφ′为

3.2 功率因数角与系统参数的关系

由式（4）与式（5）可知，网侧功率因数角φsi以及TSMC输入侧功率因数角iφ′与输入滤波器、负载、调制比和功率因数设置角φi等系统参数都有关系。以下分别讨论各个系统参数对功率因数角的影响。

3.2.1 调制比m的影响

设各参数为：Rf=20Ω，Lf=1mH，Cf=25μF，输入电压频率fi=50Hz，输出电压频率fo=60Hz，负载Rl=25Ω，Ll=10mH。图 2a、2b分别为调制比m在[0，1]范围内变化时，网侧功率因数角φsi与功率因数设置角φi的关系曲线，以及TSMC输入侧功率因数角iφ′与功率因数设置角φi的关系曲线。

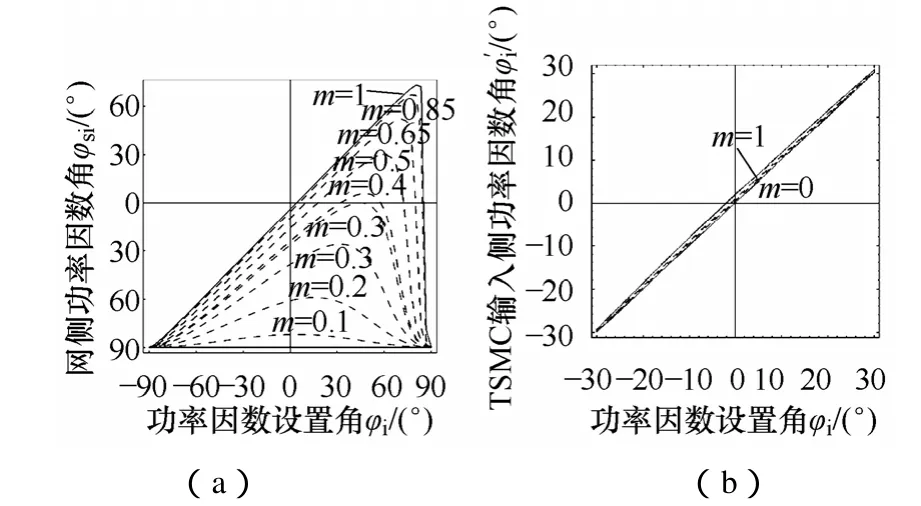
图2 调制比m对功率因数角的影响Fig.2 Effect of modulation ratio m on power factor angle

由图2a可知，当φi=0时，调制比m越小，则|φsi|越大，即m越小电流超前电压的角度越大，同时m对网侧功率因数角φsi的变化范围也会造成影响；当m=1 时，网侧功率因数角φsi可在约[-90°,75°]范围内变化，当 m=0.2 时，φsi只能在约[-90°,-60°]间变化了。由式（4）可知，当系统其他参数不变时，调节功率因数设置角φi即可控制网侧功率因数角φsi，但通过上述分析可知，随着m的减小φi逐渐失去了对网侧功率因数角φsi的调节能力，当m减小到某一特定值时，无论怎样调节功率因数设置角φi，都无法使网侧功率因数角为零，在上文各参数情况下，计算可得当m＜0.38时则无法实现网侧单位功率因数。

图2b反映了不同调制比下TSMC输入侧功率因数角iφ′与功率因数设置角φi的函数关系，可以看出调制比m对iφ′的影响不大。

3.2.2 滤波器参数的影响

图3所示为输入滤波器参数变化时，φsi、iφ′与φi的关系曲线。其他参数：调制比m=0.85（m为其他值时得到的关系曲线与图3趋势一致，它的取值并不影响本文得出的结论），输入电压频率 fi=50Hz，输出电压频率 fo=60Hz，负载 RL=25Ω，LL=10mH。

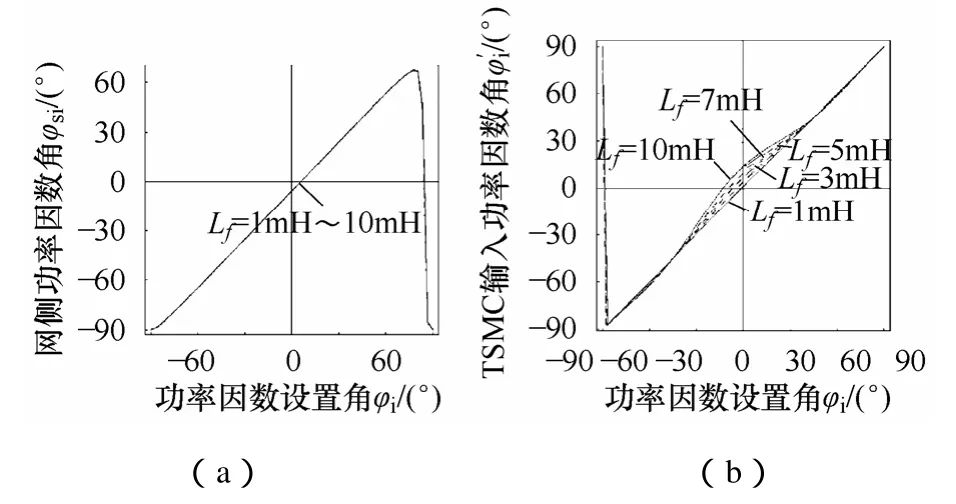
图3 输入滤波电感对功率因数角的影响Fig.3 Effect of input filter inductance on power factor angle

图3为滤波电感Lf在1～10mH间变化时，φsi、iφ′与φi的关系曲线。由图3a可知，滤波电感在1～10mH间变化时φsi的波形几乎没有任何变化，即Lf对φsi的影响不大；由图3b可知，可知当φi=0时，滤波电感Lf越大则′越大，同时Lf对功率因数设置角的调节范围也会造成影响，这一点将在之后的内容讨论。

图 4为滤波电容Cf在 10～100μF间变化时，φsi、iφ′与φi的关系曲线。由图4a可知，可知当φi=0时，滤波电容 Cf越大则|φsi|越大，即电流超前电压的角度越大；由图4b可知滤波电容Cf在10～100μF间变化时′的波形几乎没有任何变化，即滤波电容对的影响不大。

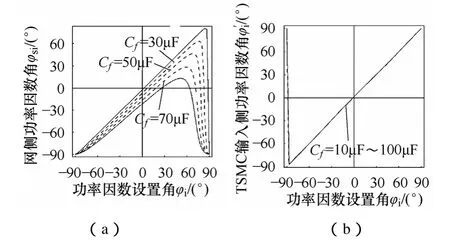
图4 输入滤波电容对功率因数角的影响Fig.4 Effect of input filter capacitance on power factor angle

3.2.3 负载的影响

以下分析负载对φsi以及′的影响，其他参数为：Rf=20Ω，Lf=1Mh，Cf=25μF，输入电压频率fi=50Hz，输出电压频率fo=60Hz。

图 5为负载阻抗角φo相同、负载复阻抗模|Zl|在10～100Ω变化时，φsi、′与φi的函数关系。由图5a可知，负载复阻抗模|Zl|越大时|φsi|越大，即越是轻载电流超前电压的角度越大；由图 5b可知|Zl|在10～100Ω变化时，′的波形几乎没有任何变化，即|Zl|对′的影响不大。

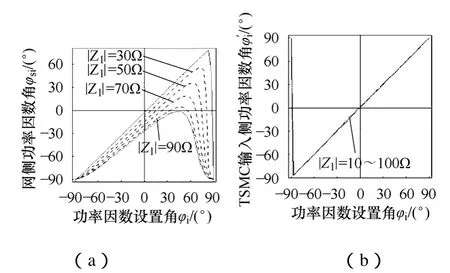
图5 负载复阻抗模值对功率因数角的影响Fig.5 Effect of complex impedance module on power factor angle

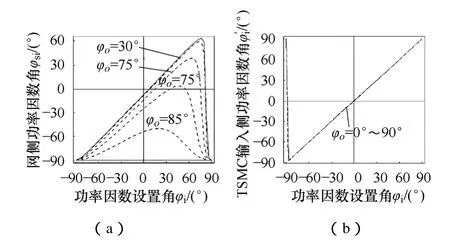
图6 负载阻抗角对功率因数角的影响Fig.6 Effect of impedance angle on power factor angle

图6为负载复阻抗模|Zl|相同、负载阻抗角φo在0～90°变化时，φsi、′与φi的函数关系曲线。由图 6a可知，感性程度越重时越大，电流超前电压的角度越大；由图6b可知φo在0～90°变化时′的波形几乎没有任何变化，即φo对′的影响不大。

综上所述，可得到以下结论：

（1）网侧功率因数角φsi与功率因数设置角φi以及系统各参数有关，其中系统的调制比m越低，输入侧滤波电容Cf越大，越是轻载、负载感性成分越重时，输入电流超前网侧输入电压的角度越大，即功率因数越低；同时以上参数还会影响网侧功率因数角φsi的变化范围，调制比越低、滤波电容越大、轻载且负载感性成分越重时，φsi的变化范围越窄。

（2）TSMC输入侧功率因数角iφ′主要取决于滤波器电感值，电感越大时，TSMC输入侧功率因数角越滞后。

3.3 网侧功率因数角φsi调节范围的分析

由上述分析可知，网侧功率因数角φsi与系统的各参数有关，当系统滤波器选定并且负载确定之后，通过更改功率因数设置角φi来控制调节网侧的功率因数角，这种方法十分简单有效。然而，为了使得TSMC安全工作，对φi调节必须在一定的范围内进行，否则可能造成TSMC直流母线电压为负值，导致整流级出现短路故障，甚至损害开关器件。

结构如图1所示的18开关TSMC运行时，必须保证中间直流环节电压时刻为正值，否则会出现短路故障，这就是确定功率因数设置角φi调节范围的重要约束条件。文献[10]已经对输入功率因数的调节范围得出了结论：TSMC输入侧功率因数角的调节范围为[-30°,30°]。由上文可知，TSMC输入侧功率因数角′主要取决于滤波器的电感值，如图7a所示，显然滤波电感越小，满足在[-30°,30°]范围内的功率因数设置角φi的可调范围越大，如当Lf=3mH，φi可在约[-31°,29°]间变化，当 Lf=7mH，φi就只能在约[-33°,25°]间变化了，因此在满足截止频率的条件下应尽量减小滤波器电感的取值。同时，由于功率因数设置角φi受到限制，网侧功率因数角的可调范围也受到影响。

图7 功率因数角的可调范围Fig.7 Adjustable range of power factor angle

图 7b 为功率因数设置角φi在[-90°,90°]范围内网侧功率因数角φsi与调制比m的关系曲线。当功率因数设置角φi的可调范围在[-33°,25°]之间时，图中红色区域为网侧功率因数角φsi的可调范围。可见当功率因数设置角的可调范围不同时φsi的可调范围也会变化。同时由图可知，调制比m越大，φsi的可调范围越宽。当 m=1时，φsi的可调范围为[-37°,20°]；但当m＜0.43后，网侧功率因数角曲线在[-33°,25°]之间与横轴无交点，这时无论如何调节功率因数设置角都无法将网侧功率因数角φsi调节至0°，因此，无法实现网侧功率因数为“1”。同理也可以得到当滤波电容过大、负载复阻抗模过大（轻载）或负载阻抗角φo过大（感性）时，通过调节功率因数设置角也无法实现网侧单位功率因数。

值得注意的是以上分析只针对 18开关的TSMC，若 TSMC整流级与逆变级均使用双向开关构造，则理论上功率因数设置角φi可为[-90°,90°]的任意值，这时网侧功率因数角的可调范围也大大增加了，图7中当m=1时，φsi的可调范围为[-90°，74°]。

4 TSMC网侧功率因数闭环控制策略

从式（4）可知，改变功率因数设置角φi即可调节网侧功率因数角φsi及网侧功率因数。功率因数设置角φi的物理意义为TSMC输入相电压与期望输入相电流间的相位差，如图8所示。图中θUs为输入相电压瞬时相位，θIs为期望输入相电流的瞬时相位，φi=θUs-θIs。

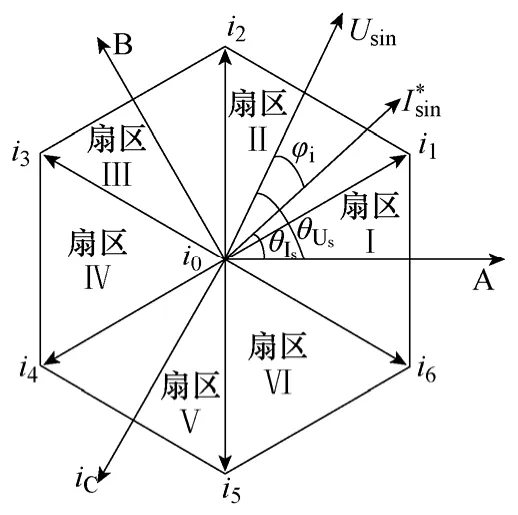
图8 电流空间矢量及功率因数设置角φi定义Fig.8 Current space vector and definition of power factor angle φi

通常，矩阵变换器的功率因数角采用开环控制方式，即将功率因数设置角φi给定为某一偏置量，该方法只能在某一特定工况下实现单位功率因数。为解决这一问题，本文提出了一种功率因数闭环控制方法，其控制原理框图如图9a所示。通过检测输入电流与输入电压，计算出两者的相位差，利用PI调节器对实际相位差与期望相位差（设置为零）进行实时调节。

图9a中，θUs表示输入电压相位，θIs表示输入电流相位，φi表示输入电压、电流间的相位差（即实际功率因数角）。表示功率因数角的给定值。系统的闭环控制传递函数框图如图9b所示。系统输入与输出间的偏差量 E(s)即为输入电压与输入电流间的相位差，可由下式求得：

式中，θU(s)、θI(s)分别为输入与输出量的拉氏变换；φI(s)为期望相位差的拉氏变换，设期望相位差为，则 φi( s) =/s ；Gφ(s)为PI调节器的传递函数，

由式（6）可得系统的稳态相位差为

由式（7）可以看出，在闭环控制下输入电压电流之间的相位差的稳态值为。若设期望相位差为=0，则可实现系统的单位功率因数运行，因此该闭环控制系统可实现良好的功率因数角控制。

图9 网侧功率因数闭环控制原理框图与传递函数结构图Fig.9 Control principle diagram and closed loop control transfer function schematic of grid side power factor

由前文分析可知功率因数角φi必须在一定范围之内，否则TSMC将出现短路故障，因此应根据滤波电感参数限制PI调节器的输出上限与下限值，本文为保证一定的安全裕量，PI调节器的输出上限与下限值为±26°。

5 仿真与实验验证

为了验证上面分析的网侧功率因数受系统参数影响的正确性，利用Matlab软件对系统进行了建模仿真。图10为系统参数发生变化时输入电压与电流相位差的仿真结果。0～0.04s时，调制比 m=0.9、滤波电容 Cf=20μF、负载 Rl=20Ω、Ll=10mH，此时相位差约为-17.5°；0.04s时，滤波电容 Cf由 20μF变为30μF，此时相位差变约为-21.5°；0.06s时，负载电感由 10mH变为 100mH，此时相位差变为约-3 3.75°；0.08s时，调制比由0.9变为0.5，此时相位差变为约-74°。由上述仿真结果可知网侧功率因数受系统参数影响的分析正确。

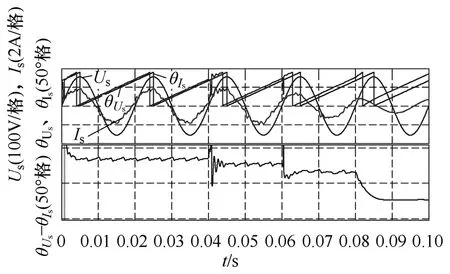
图10 系统参数对网侧功率因数角的影响Fig.10 Effect of system parameters on grid side power factor

图11a是输入功率因数设置角分别为±15°、±30°、±60°时的中间电压波形。0～0.02s时，输入功率因数设置角φi=0°；0.02～0.06s时，φi=15°；0.06～0.10s时，φi=30°；0.10～0.14s 时，φi=60°；0.14～0.18s时，φi=0°；0.18～0.22s时，φi= -15°；0.22～0.26s时，φi= -30°；0.26～0.30s时，φi= -60°。仿真结果表明当φI＞30°或φi＜-30°时中间电压出现小于零的情况。图11b为各功率因数设置角所对定的输入电压、电流、相位以及相位差波形，反映了输入功率因数设置角对网侧功率因数角的调节作用。

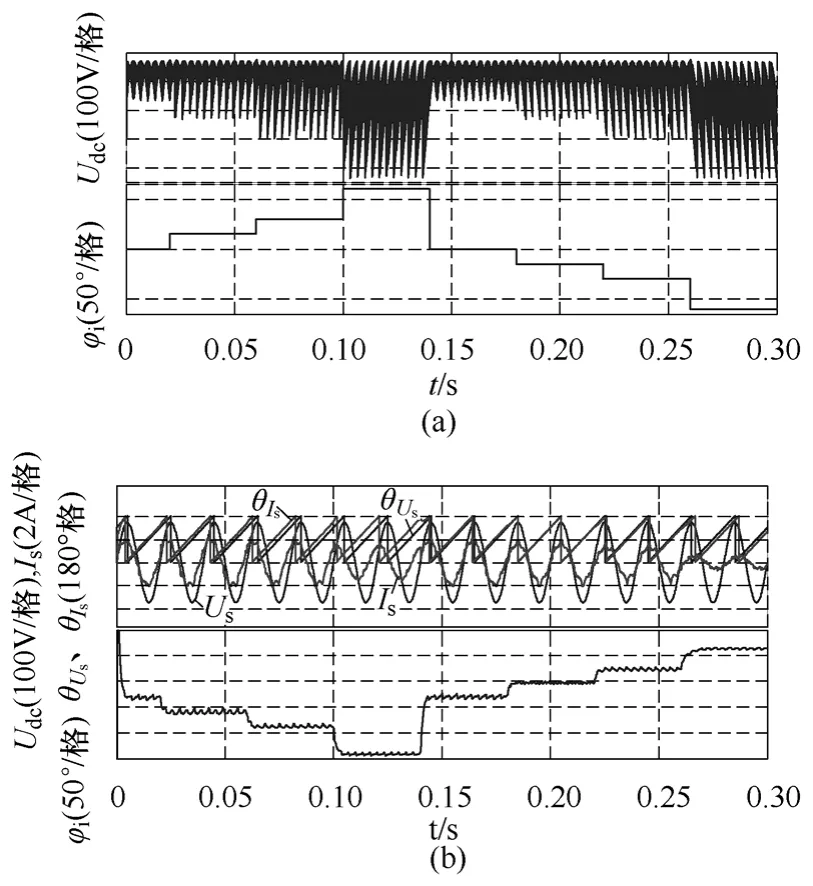
图11 功率因数设置角对直流母线电压以及网侧功率因数角的影响Fig.11 Effect of setting power factor angle on dc-link voltage and grid side power factor angle

为了验证所提出的网侧功率因数动态补偿方案的可行性，在基于DSP+CPLD 控制的TSMC实验样机上进行了实验验证。实验中采用三相调压器作为网侧电源，输入滤波器电感 Lf=3mH、电容 Cf=1 3.75μF、Rf=20Ω，Rl=40Ω、电感 Ll=5mH。实验波形如下。

图12a、12b为未进行网侧功率因数控制时的实验波形。Us与Is分别为输入电压与输入电流波形，θUs与θIs为输入电压相位与输入电流相位，图 12b为图12a时基放大后的波形，可以看出未进行输入相位闭环时，电流超前电压约600μs，即10.8°左右。图12c为未进行网侧功率因数控制时中间直流母线电压波形与输出线电压波形。

图12 未补偿时实验波形Fig.12 Experimental waveforms without compensation

图13为进行网侧功率因数控制后的实验波形。图13b为图13a时基放大后的波形，可以看出当进行输入相位闭环控制时，输入电压与输入电流的相位差为零，可以实现单位功率因数。图13c为中间直流母线电压波形与输出线电压波形，与图12c比较可以看到直流母线电压波形明显不同，与仿真结果（见图11）相一致。

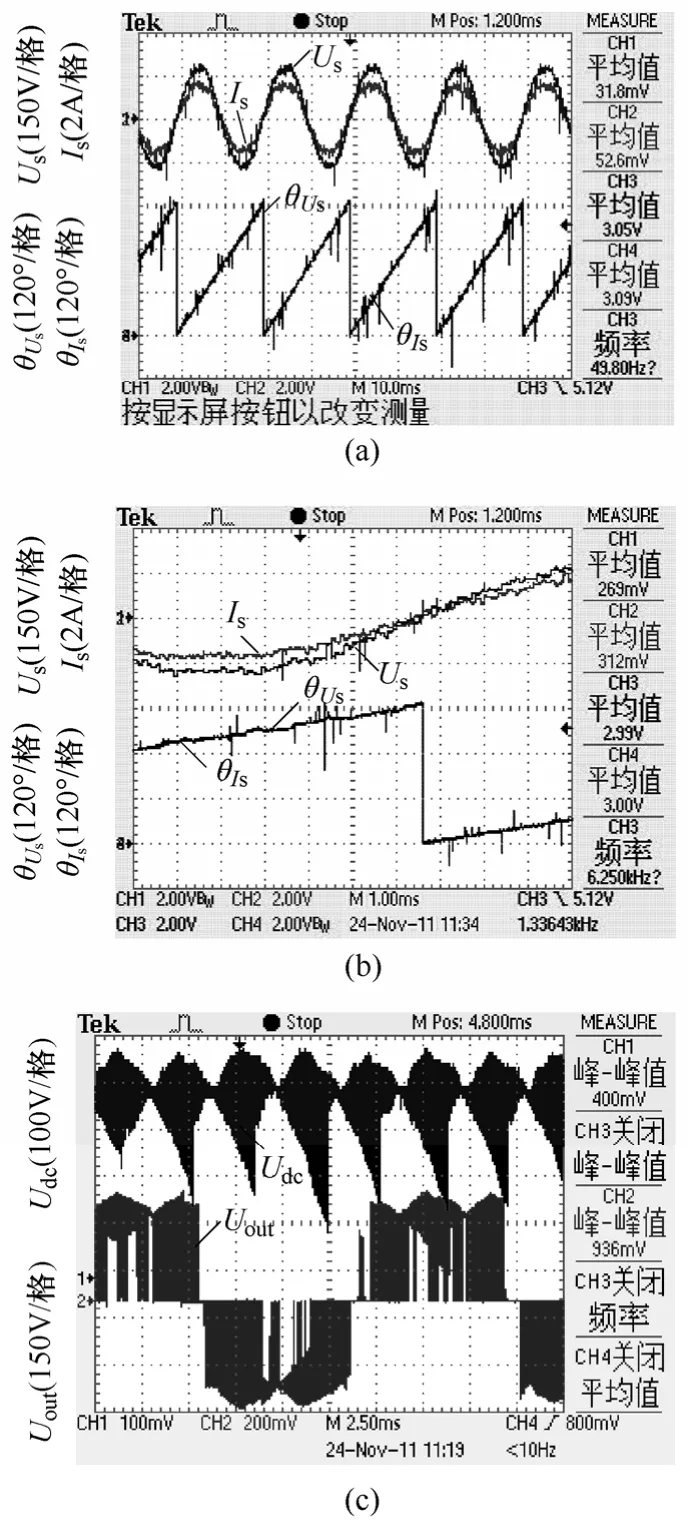
图13 补偿后实验波形Fig.13 Experimental waveforms with compensation

为验证控制策略的动态补偿特点，本文做了负载突变实验。图14a为未进行输入相位闭环时，负载电阻由40Ω突变到1 3.3Ω的输入电压Us、输入电流 Is以及相位差θUs-θIs波形，由图可以看出当负载突变时电流超前角度增大；图14b为进行输入相位闭环后，负载电阻由 40Ω突变到 1 3.3Ω的输入电压Us、输入电流 Is以及相位差θUs-θIs波形，由图可以看出经过补偿控制，负载发生突变前后相位差始终为零。图15a、15b分别为开环与闭环时负载电阻由1 3.3Ω突变到40Ω的输入电压Uin、输入电流Iin以及相位差θUin-θIin的波形。由实验波形可知，相位闭环控制的效果很好。

6 结论

图14 未加入闭环情况下负载突变时实验波形Fig.14 Waveforms of load changing under open-loop situation

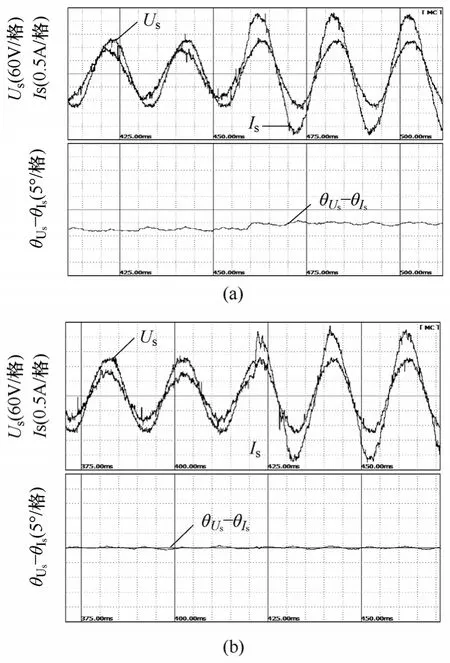
图15 加入闭环情况下负载突变时实验波形Fig.15 Waveforms of load changing under close-loop situation

本文通过建立TSMC系统数学模型，得到了网侧功率因数角以及TSMC输入侧功率因数角的解析表达式。在此基础上，首先详细分析了系统各参数对网侧功率因数角以及TSMC输入侧功率因数角的影响；其次得出了网侧功率因数角的可调范围，并分析了其可调范围与系统参数的关系；最后提出了一种简单的网侧功率因数闭环控制方案，使系统不仅在静态时可以实现单位功率因数控制，而且在系统参数发生变化时，也可以完成网侧功率因数补偿。

仿真与实验结果表明了本文理论分析的正确性以及控制方案的有效性。

附 录

[1]郭燚.船舶电力推进双三相永磁同步电机驱动控制研究[D].上海: 上海海事大学,2007, 69-70.Guo Yi.Double-three-phase permanent magnet synchronous motor drives control for the vessel electric propulsion[D].Shang hai: Shanghai Maritime University,2007, 69-70.

[2]Johann W Kolar, Frank Schafmeister, Simon D R.Novel three-phase AC-AC sparse matrix converters[J].IEEE Transactions on Power Electronics,2007,22(5):1649-1661.

[3]Kolar J W, Baumann M.Novel three-phase AC-DCAC sparse matrix converter[C].Proceedings of 17th IEEE Applied Power Electronics Conference and Exposition,2002,2 : 777-791.

[4]Clumpner Blaabjerg C F.Two-stage matrix converteran alternative to the matrix converter[C].IEEE Professional Networks on Power Conversion and Applications.United Kingdom, London,2003: 61-69.

[5]孙凯, 周大宁, 梅杨.矩阵式变换器技术及其应用[M].北京: 机械工业出版社,2007.

[6]Jussila M, Salo M, Tuusa H.Realization of a threephase indirect matrix converter with an indirect vector modulation method[C].Proceeding of 34th IEEE Applied Power Electronics Conference,2003: 689- 694.

[7]邓文浪, 杨欣荣, 朱建林.基于 dq稳态模型的双级矩阵变换器功率特性研究[J].系统仿真学报,2008,20(11): 2846-2850.Deng Wenlang, Yang Xinrong, Zhu Jianlin.Power characteristics analysis of two-stage matrix converter based on dq steady model[J].Journal of System Simulation,2008,20(11): 2846-2850.

[8]Kwak Sangshin.Indirect matrix converter drives for unity displacement factor and minimum switching losses[J].Electric Power Systems Research,2007,77(6): 447-454.

[9]宋卫章, 钟彦儒, 李洁.带相位补偿环节的双级矩阵变换器网侧电流闭环控制[J].电工技术学报,2010,25(7): 77-84.Song Weizhang, Zhong Yanru, Li Jie.Input current feedback control strategy with phase compensation component for two-stage matrix converter[J].Transactions of China Electrotechnical Society,2010,25(7): 77-84.

[10]陆晓楠, 孙凯, 李刚, 等.双级矩阵变换器网侧功率因数的控制方法[J].电工技术学报,2010,25(10):108-114.Lu Xiaonan, Sun Kai, Li Gang, et al.Control method analysis of grid side power factor in two stage matrix converter[J].Transactions of China Electrote- chnical Society,2010,25(10): 108-114.

[11]王晶鑫, 姜建国.基于预测算法和变结构的矩阵变换器驱动感应电机无差拍直接转矩控制[J].中国电机工程学报,2010, 30(33): 65-70.Wang Jingxin, Jiang Jianguo.A deadbeat direct torque control strategy with prediction algorithm and variable structure controller for induction motor driven by matrix converter[J].Proceedings of the CSEE,2010, 30(33): 65-70.

[12]史明明, 周波, 魏佳丹.HESG-MC发电系统恒调制比电压闭环控制策略[J].中国电机工程学报,2011,31(15): 101-106.Shi Mingming, Zhou Bo, Wei Jiadan.HESG-MC generations system voltage close loop control strategywith constant modulation ratio[J].Proceedings of the CSEE,2011, 31(15): 101-106.

[13]张绍, 周波.非对称输入下矩阵变换器新型电流控制策略[J].电工技术学报,2009,24(3): 47-54.Zhang Shao, Zhou Bo.Improved current control strategy of matrix converter under unbalanced inputs[J].Transactions of China Electrotechnical Society,2009,24(3): 47-54.