基于交通波的高速公路事故的交通影响分析

余贵珍 刘玉敏 金茂菁

(北京航空航天大学 交通科学与工程学院，北京100191)(科学技术部高技术研究发展中心，北京100044)

王云鹏

(北京航空航天大学 交通科学与工程学院，北京100191)

高速公路交通事故在给人们带来生命财产损失的同时，也会引发大范围的交通拥堵，增加车辆油耗和废气排放，带来能源消耗和环境污染问题.高速公路上一旦发生交通事故，部分道路就会被占用或者封闭，事故发生地点通行能力降低，无法满足交通需求，进而导致交通拥堵，增加二次事故发生的可能性.因此，重视高速公路交通安全，正确合理地分析高速公路交通事故点的交通流动态特性，估算高速公路事故带来的交通影响，是高速公路交通事故管理的重要内容，也是交通事故及时有效处置的基础［1］.

近年来，交通事件是交通领域中的重要课题之一，高速公路交通事件问题备受关注，国内外学者对此进行了诸多研究和探索.其中多是针对交通事件分析的研究，并且侧重于交通事件的延误分析.研究分析采用的交通流理论主要有确定性排队理论和交通波理论.文献［2］对交通波理论作了深入研究，对不同交通状况下交通事件的延误情况进行了分析，提出一种基于交通波理论计算交通事件总延误的模型计算方法，但是该方法计算得出的总体延误时间与实际延误时间相比误差较大.尤其与一些商业化的微观交通仿真软件仿真结果相比，总体延误偏小，误差较大［2］.文献［3］在交通时间的影响分析中，主要使用交通波理论定性分析交通事件，而未给出具体的交通影响估算方法.唐铁桥等人［3］通过描述走走停停的非均衡交通现象对两车道交通流的交通波特性进行了分析说明，但是未对事故情况下的交通波进行分析.文献［4］考虑了不同时间段内不同阻塞行车道宽度的车辆排队长度，对交通事故影响下不同时间段内交通流量变化进行了分析，为异常事件下的交通流预测奠定基础.曹志远等人［4］建立了事故状态下的交通分析模型，推导出事故影响线消散时空影响范围，从而得到了事故全过程的解析解.

交通事件影响分析是高速公路系统分析中的一个重要方面，交通事故作为最典型的偶发性交通事件，其影响分析对高速公路实施有效交通控制、事故快速处理、交通诱导管理及公路规划等都有重要的作用.高速公路事故的交通影响分析主要针对交通事故发生后事故点上游车辆的排队时空影响进行分析，为降低交通事故带来的拥堵影响和优化交通事故管理提供理论依据.本文以交通波理论为基础，对由高速公路交通事故引起的交通波传播特性进行分析，以两车道的交通事故为例，对交通事故中交通波的时空演化过程进行建模，建立事故的交通时空影响数学模型，并以商业化的微观交通仿真软件Q-Paramics对本事故影响模型进行仿真实验验证.

1 事故的交通波传播分析

交通波理论是基于流体动力学建立起来的一种交通流理论［5］，它描述了同向运动不同状态的两股交通流相遇时的交通状态转移过程［6］，即当道路交通因为交通状况的改变而发生车流密度变化时，不同状态的交通流(交通流量、交通密度、平均速度分别为 qi，ki，vi与 qj，kj，vj)相遇并产生交通波，其交通波的传播速度 Wji=(qj－qi)/(kj－ki)，使用交通波理论可定量分析车流的积聚和消散过程.

本文主要以两车道高速公路为研究对象，不考虑出入口匝道对交通流影响，并假设事故地点上游车流量稳定，车辆到达率恒为一定值.多车道的交通影响分析模型可以参考此两车道交通影响分析模型.

通常交通事故的发生过程如下:在tA时刻时，在高速公路横断面A处发生一起交通事故，事故发生后该方向上的所有交通即刻封锁并进行事故处理;在tB时刻，一条车道完成清理工作，该车道上的车辆恢复行驶;在tC时刻，另一条车道也清理完毕，道路全面通车，所有车辆恢复正常行驶.

分析事故发生后的交通影响，可将交通波传播过程分为以下几个阶段:

1)当t=tA时，在高速公路某横断面上发生交通事故，该方向上的所有交通即时被封锁，交通状况如图1.此阶段路段中出现波速为 W21=的交通波(q1，k1为事故前自由流状态下事故发生地的交通流量和交通密度，q2，k2为事故发生后紧临事故地点的交通流量和交通密度).

图1 事故发生初期

2)当t=tB时，车道1被清理，部分车辆恢复行驶，交通状况如图2所示.车道1恢复初期，道路上有两股交通波，波速分别为 W21和 W32=表示车道1被清理后事故地点的交通流量和交通密度)，此状态持续到W21和W32两波相遇时刻为止.

图2 车道1被清理初期

3)车道1交通恢复后期，即从W21和W32两波相遇时刻开始到两车道清理前的时间，道路上仅有交通波(如图3所示).

图3 车道1交通恢复后期

4)当t=tC时，全部道路清理完毕.初期阶段，道路上有交通波和表示两车道均被清理后事故地点的交通流量和交通密度)，此状态持续到W43和W31两波相遇时刻为止(如图4所示).

图4 两车道清理完毕初期

5)W43和W31两波相遇时刻开始到交通恢复正常为止.道路上仅有交通波，交通波W41完成后，交通恢复正常(如图5所示).

图5 交通恢复正常初期

2 两车道事故交通影响模型

根据交通波的传播特性，可以通过图6所示的交通事故时空演化图描述事故发生后的车辆排队过程.事故发生在tA时刻，距离为L的横断面上，两条车道全部封堵，产生交通波W21;在tB时刻，其中一条道路清理，产生交通波W32，并在tD时刻与W21相遇，形成新的交通波W31;在tC时刻，两条车道全部清理，产生交通波W43;在tE时刻与W31相遇，形成新的交通波W41;在tF时刻，事故的影响全部消除，交通恢复正常.

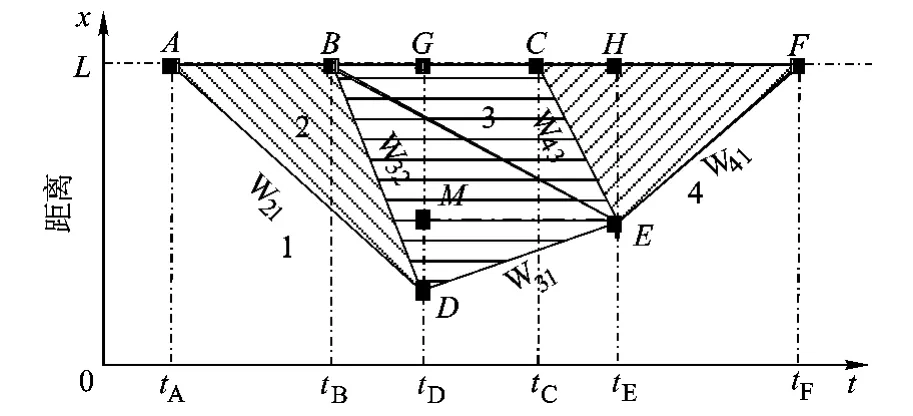
图6 事故影响时段内的排队过程

如图，已知点 A(TA，L)，B(TB，L)，C(TC，L)和交通波速度 W21，W31，W41，W43，W32，根据几何代数关系，可求出关键节点D，E，F处的坐标，从而可确定事故的空间交通影响范围和关键时间节点(以下公式中的Wij均表示Wij的绝对值).

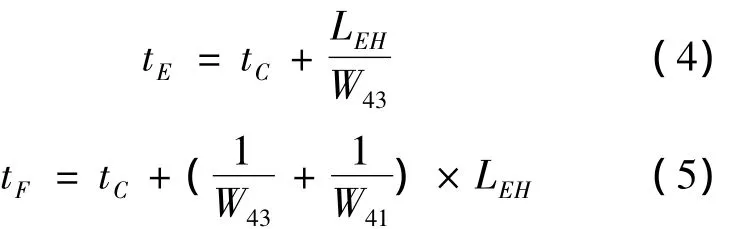
由此可得事故的空间影响为

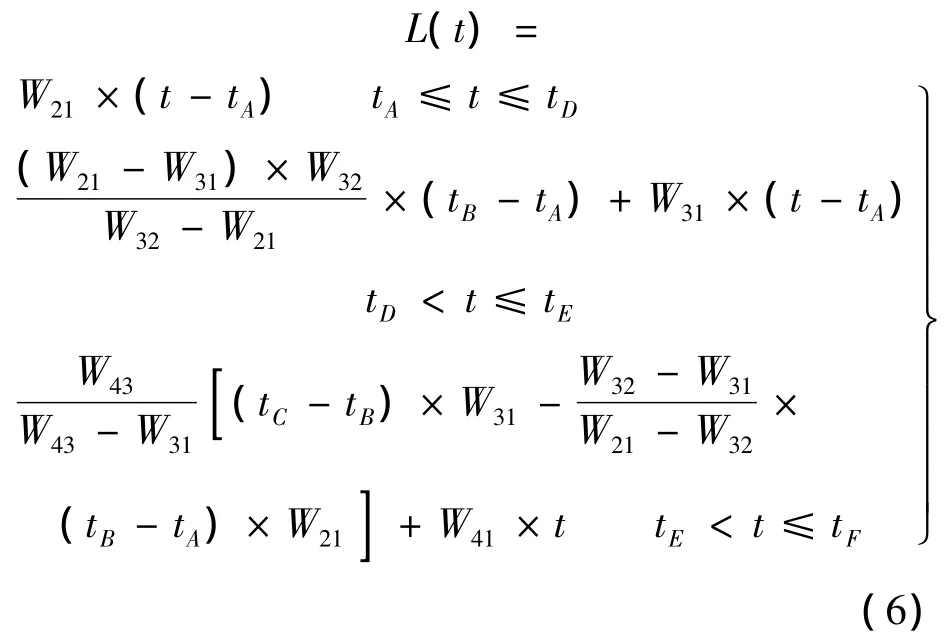
通过交通波传播特性分析，可以得出事故最长影响距离为

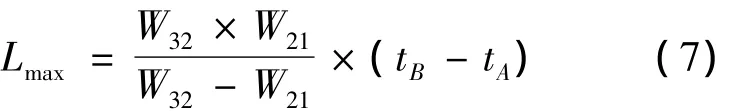
事故最长影响时间为

获取事故发生地和发生时间后，根据模型所计算的事故最长影响距离和最长影响时间，可以快速准确确定事故的时空影响范围.事故的时空影响范围为事故分析决策和事故处置提供了可靠的执行依据.

3 数值计算实例

考察某两车道高速公路，其通行能力为1800 pcu/h/ln，车辆最大行驶速度为60 km/h，堵塞车流密度为65 pcu/km/ln.事故发生前公路上车辆的流量和密度分别为1600 pcu/h/ln和33.3 pcu/km/ln，由于某随机原因在tA=0时刻偶然发生了交通事故，事故发生后tB=0.5h时，第1条车道被清理，tC=1.0 h第2条车道被清理完毕并通车.根据上述分析，可以用如下的交通流量-密度图(q-k)表示交通波的计算过程，其中图7为两车道的高速公路的交通流-密度图.记点1为交通事故发生时刻的交通状况，点2为交通事故发生时刻后道路交通全部中断的交通状况，点3为部分道路清理后的交通状况，点4为全部道路清理后的交通状况，两点连线的斜率分别为交通波的传播速度.

在两车道道路的交通流量-密度图曲线中，一条道路和两条道路最大速度、最大流量和堵塞密度分别为

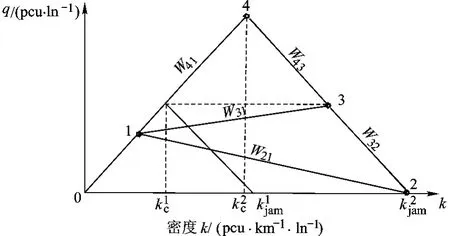
图7 两车道高速公路交通流-密度图

可得出:

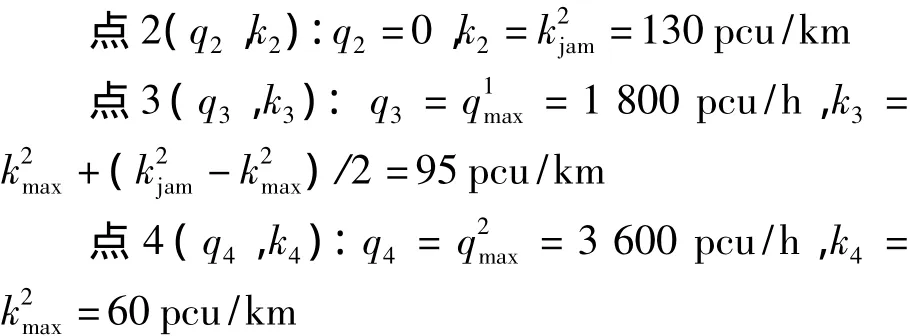
设 q1=1600 pcu/h，k1=33.3 pcu/km，(W ＜0表示交通波向上游传播，L＜0表示车队在事故发生地的上游)，因此由Wji=(qj－qi)/(kj－ki)可得

tA，tB，tC分别为 tA=0，tB=0.5 h，tC=1.0 h，由式(1)、式(2)计算得两个关键时间节点的事故影响范围为

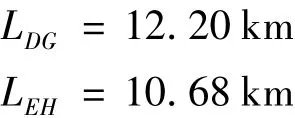
经过多次仿真实验，由式(8)可得，本计算实例所述交通条件下，交通事故影响时间为

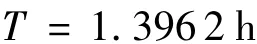
4 仿真实验与分析

为了验证以上事故影响分析方法和计算公式的有效性，本文中采用集成化的交通微观仿真软件Q-Paramics作为仿真验证工具.

方案设计如上述案例，选取两车道的高速公路作为研究对象，用所建立的事故影响模型进行事故影响范围的估算.利用Q-Paramics软件中的建模器Modeller搭建两车道的高速公路交通事故模型，设置仿真路段长度为10 km，在仿真开始后10 min在路段下游10 km处发生交通事故，在22 min时一条道路被清理，在28 min时另一条道路被清理.仿真时将路段交通流量分别设置为800～1 600 pcu/km/ln，进行多次反复仿真模拟.由于Q-Paramics是随机仿真程序，如果输入的随机数种子相同，将得到同样的仿真结果.因此，实验时使用重复运行的仿真方法，同时为降低仿真带来的随机性，对上面的仿真方案改变随机数种子仿真模拟20组数据，并取20次仿真的平均结果用于比较.

利用分析器Analyser进行仿真数据的分析提取，包括车辆行驶路线、路段交通流量、最大车队长度、交通密度、车辆速度和延误时间等.分别在道路饱和程序不同的情况下分别进行交通仿真与模型估算，本研究选取了3个评价指标，分别是最大排队长度LDG，关键排队长度LDG，和交通事故时间影响T，计算结果与仿真结果的比较图如图8～图10所示.

图8 最大排队长度LDG比较图

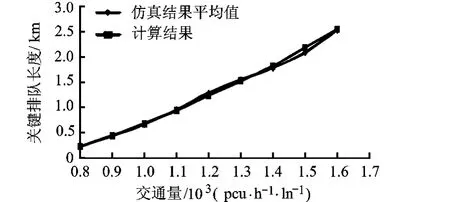
图9 关键排队长度LEH比较图

图10 交通事故时间影响T比较图

从以上3图可以得出，在相同的道路条件下，当事故上游的交通量增大时，仿真结果和模型计算结果所得出的最大排队长度、关键排队长度都增长，交通事故时间影响也逐渐扩大，并且3个评价指标总体呈线性递增.当交通量为1200 pcu/h/ln时，即最接近道路通行能力时仿真结果与模型计算结果的误差最小.在模型计算时，以交流量为1200 pcu/h/ln作为基准考虑车辆启动和停止时的相互影响.而在仿真或实际的交通中，当道路交通流稀疏时，道路上车辆的间距较大，车辆的行驶受到周围车辆的影响较小，仿真的交通事故时间影响明显小于模型计算，并随交通流量减小，仿真的交通事故时间影响与模型计算误差变大.当道路上的交通量大于1200 pcu/h/ln时，车辆行驶受周围车辆的影响较大，仿真的交通事故时间影响大于模型计算，并随交通流量增大，仿真的交通事故时间影响与模型计算误差变大.

经Q-Paramics仿真实验验证，可得出上述计算公式所得结果与仿真实验所得结果的平均误差小于5%，较准确地估算交通事故的时空影响，此误差精度能够较好满足事件影响要求10%左右误差的实际需求.

5 结论

本文利用交通波理论，以两车道高速公路为例进行交通事故后的交通波传播特性分析，对事故后的交通波进行时空演化分析，建立数学模型，估算事故的时空影响范围，并进行了实例验证分析.研究结果表明，该模型能够快速有效地计算出发生交通事故后的排队长度和交通事故的持续影响时间，为高速公路管理和控制部门定量估算交通事故的交通延误时间提供重要依据.但由于事故发生时间、事故类型、道路车道数量等对交通流造成的复杂影响，要求进一步研究各种事故因素与交通事故影响的内在联系，并对实际的交通事故案例进行验证分析.另外高速公路事故的交通影响分析仅停留在时空角度，还需要更加精确定量地分析交通事故所带来的总体延误，本文将在随后的工作中进行事故的延误模型的相关研究.

References)

［1］喻军皓.交通事故对城市道路交通状态的影响研究［D］.上海:同济大学交通运输工程学院，2010 Yu Junhao.Research on the influences of traffic accidents upon urban traffic conditions［D］.Shanghai:School of Transportation Engineering，Tongji University，2010(in Chinese)

［2］Chien S J，Goulias D G，Yahalom S，et al.Simulation-based estimates of delays at freeway work zones［J］.Journal of Advanced Transportation，2002，36(2):131 －156

［3］唐铁桥，黄海军.两车道交通流的波动分析［J］.北京航空航天大学学报，2005，31(10):1121 －1124 Tang Tieqiao，Huang Haijun.Wave properties of a traffic flow model for freeways with two lanes［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31(10):1121 －1124(in Chinese)

［4］曹志远，郭忠印，张起森，等.高速公路重大交通事故时空影响范围研究［J］.公路工程，2011，36(6):55 －58 Cao Zhiyuan，Guo Zhongyin，Zhang Qisen，et al.Research on time and spatial extent of terrible traffic accident on highway［J］.Highway Engineering，2011，36(6):55 －58(in Chinese)

［5］王殿海.交通波理论［M］.北京:中国教育出版社，2002 Wang Dianhai.Traffic flow theory［M］.Beijing:China Communications Press，2002(in Chinese)

［6］杨少辉，王殿海，董斌，等.信号交叉口起动波模型修正［J］.公路交通科技，2006，23(1):130 －134 Yang Shaohui，Wang Dianhai，Dong Bin，et al.Modify of the start wave mode in signalized intersections［J］.Road Traffic Science and Technology，2006，23(1):130 －134(in Chinese)