改进SA模型对翼型分离流动的数值模拟
周大高 柳阳威 文晓庆 陆利蓬
(北京航空航天大学能源与动力工程学院,北京100191)
叶片是风力机结构中的关键部件,其性能决定了风力机的风能转化效率.因此,准确的对风力机叶片进行气动性能计算进而优化叶片的设计具有重要的意义.近年来,随着(CFD,Computational Fluid Dynamics)技术的发展,采用CFD对风力机气动性能进行模拟得到了广泛地应用.CFD能够反映流场内流动机理及叶片所承受气动载荷的细节,有利于指导设计者改进叶片气动外形和局部结构强度等[1].马林静等人[2]采用 3 种湍流模型(单方程SA模型、两方程k-ε模型和SST k-ω模型),对美国National Renewable Energy Laboratory(NREL)风力机翼型S825进行了二维数值模拟;通过数值计算结果与实验数据[3]进行比较,在这3种模型中SA湍流模型进行气动性能预测相对精度较高.任年鑫等人[4]考虑到失速现象出现后数值模拟的湍流动能耗散项的计算偏差,提出对SST k-ω模型耗散项相关参数的修正,并起到一定的效果.
现阶段通过传统湍流模型对风力机翼型大分离下的流动仍难以给出令人满意的模拟结果,其根本原因是现有的湍流模型不能正确模拟分离流动下湍流的强非平衡输运特性.因此,本文基于对流场湍流输运特性的分析,提出改进传统SA模型的方法,数值模拟结果表明采用该方法对翼型分离流动的模拟能力有显著的提高.
1 数值方法
算例是美国NREL水平轴风力机专用S系列翼型S825,最大相对厚度17%(相对弦长),具体叶型参数及相关实验参见文献[4].计算的攻角范围 -6.04°~20.06°,涵盖了翼型边界层附着和分离的情形.计算采用了SA模型、标准k-ε模型(SKE),SST k-ω 模型(SST)和 Reynolds Stress模型(RSM)4种湍流模型.
1.1 计算网格
本文使用Gambit生成计算网格,网格为C型四边形网格(见图1).在保证壁面第1层网格y+≈1的基础上,对翼型壁面上不同网格数目和计算域远场距壁面距离进行了对比分析,分别选取了4种网格(见表1),将采用不同网格计算得到的升力系数进行了对比(见图2),可以看出远场距壁面20倍弦长的网格可认为可行的.本文选取了Case3的网格进行后面的数值计算.

图1 网格局部放大图

表1 4种计算网格
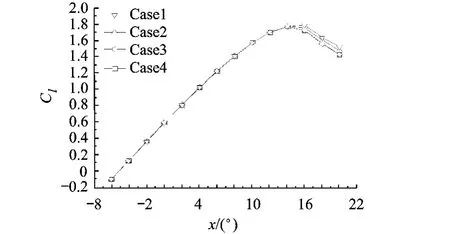
图2 4种网格计算得到的升力系数
1.2 计算条件
计算域远场采用压力远场边界条件,翼型表面定义为无滑移壁面.远场来流密度 ρ=1.177 kg/m3,静压 p=101 325Pa,静温 T=300 K,来流速度 M=0.1,流体动力粘度系数 μ=1.789×105kg/(m·s),雷诺数 Re=1.02 ×106.计算中采用SIMPLE算法,对流项采用二阶迎风差分格式.
2 SA模型简介及改进方法
2.1 SA模型简介
SA湍流模型最早在1992年在文献[5]中提出,之后在1994年他们对模型常数又进行了一些修改.它是直接利用经验和量纲分析,从最简单的各向同性湍流流动到近壁区低Reynolds流动,逐次推导和模化而得到的.
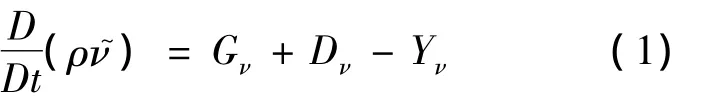
式中,Gν,Dν和Yν分别为湍流粘性生成项、粘性扩散项和粘性耗散项,具体如下:

式(2)~式(4)中,出现的相关模型函数如下:
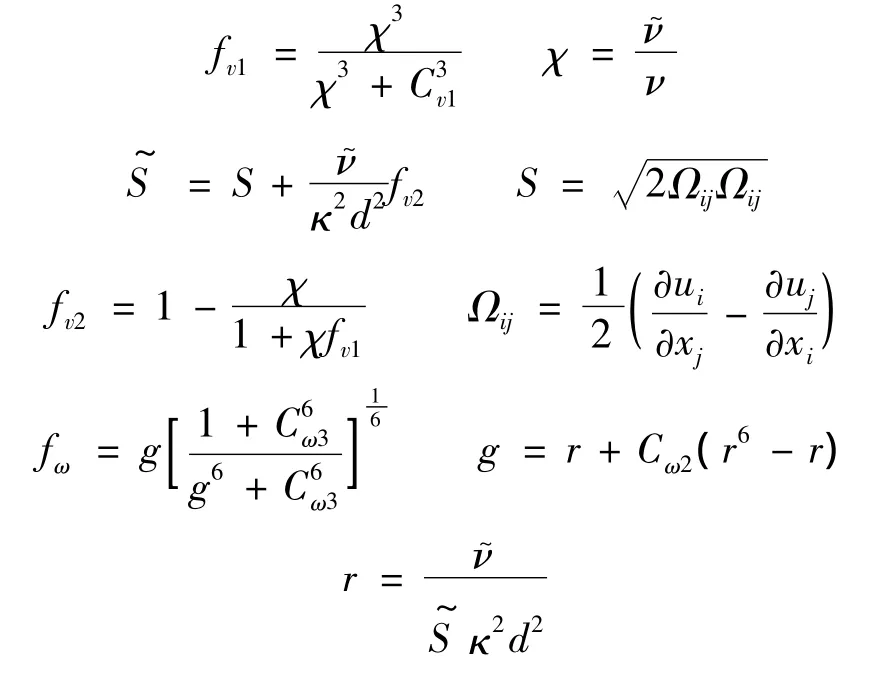
式(2)~式(4)中,ν,μ分别为分子运动粘性系数和分子动力粘性系数.
式(2)~式(4)中,出现的模型常数如下:Cb1=0.133 5,Cb2=0.622,σν~=2/3,Cν1=7.1,
2.2 SA模型改进方法
由SA模型的输运方程式(1)可知,SA模型对于湍流流场的模拟,主要是通过湍流粘性的生成、扩散以及耗散来描述湍流粘性的输运过程.而在流场中大部分地区湍流粘性生成项Gν和耗散项Yν在湍流输运的过程中所占的比重最大,它们对输运过程的不同贡献决定了流场内湍流非平衡程度的高低,对模拟的结果起主要影响.因此,只有正确预估输运方程中的生成项Gν和耗散项Yν,才能正确预估流场内湍流的输运特性以及流场的详细信息.
SA模型输运方程中的常数是基于简单流动,根据经验和量纲分析得到的,这些简单流动中湍流输运特性一般处于平衡状态,湍流能量的生成和耗散几乎相等.而对于本文中湍流非平衡输运特性很强的大攻角分离流动,湍流粘性的生成和耗散之间的平衡关系发生了明显的改变,对这样的流动常用的湍流模型不能准确模拟湍流的输运过程,导致预估结果域实验值存在较大的偏差.
为了合理预估湍流粘性的生成项Gν和耗散项 Yν,本课题组之前的研究表明[6]:在两项中均存在的模型系数Cb1有十分重要的影响,Cb1的变化影响着湍流粘性生成项Gν和耗散项Yν对输运过程的贡献,进而影响着非平衡湍流流场的输运过程,最终影响着整个流场的数值模拟精度.原始SA模型中Cb1主要是基于简单边界平衡湍流实验结果模化得到的,一般取为0.135 5.而对于非平衡程度很高的大攻角分离流动,采用原始SA模型中系数Cb1将不能得到合理的预估结果,因此应针对不同流动情况采用不同的Cb1数值,以此来正确预估不同流动条件下湍流粘性输运过程中生成项Gν和耗散项Yν的不同贡献.
3 结果分析
3.1 不同湍流模型结果对比
文献[4]给出在NASA Langly Low_Turbulent Pressure Tunnel测得的不同攻角下翼型表面压力系数分布的实验结果.其中无量纲压力系数定义
首先比较了SA,SKE,SST和RSM 4种湍流模型的模拟结果,如图3所示.发现前3种模型在吸力面表面为附着流时数值模拟的结果都与实验数据吻合的很好,而在大攻角分离的情况下,均不能很好地对升力系数进行准确的预测,这一结果也与文献[2]的结论一致;RSM模型考虑了流体的各向异性,直接对湍流切应力进行求解,能较好地预测分离,在流动发生分离后仍能给出较准确的数值模拟结果.
图4 比较了6.04°,18.06°攻角下原始 SA 模型RSM模型数值模拟结果与实验结果的压力系数分布,图5给出了数值模拟的流线图.由图可以看出无分离情况下SA模型计算值与实验值吻合较好;而在出现较大分离下情况下,SA模型不能正确预测分离的发生,吸力面处分离均晚于实际实验,这样导致吸力面压力系数小于实验结果,从而翼型的升力系数大于实验值;RSM模型能准确预测分离的发生,计算所得压力系数与实验值吻合较好,因此流动分离后,RSM模型模拟结果较为准确.本文在无实际实验流场数据的情况下,以RSM结果作为参考.
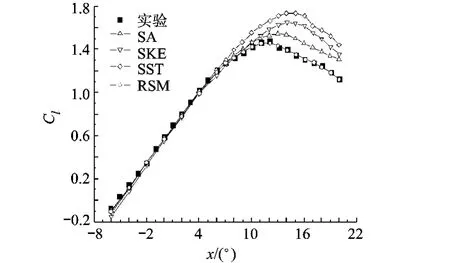
图3 不同湍流模型计算得到的升力系数
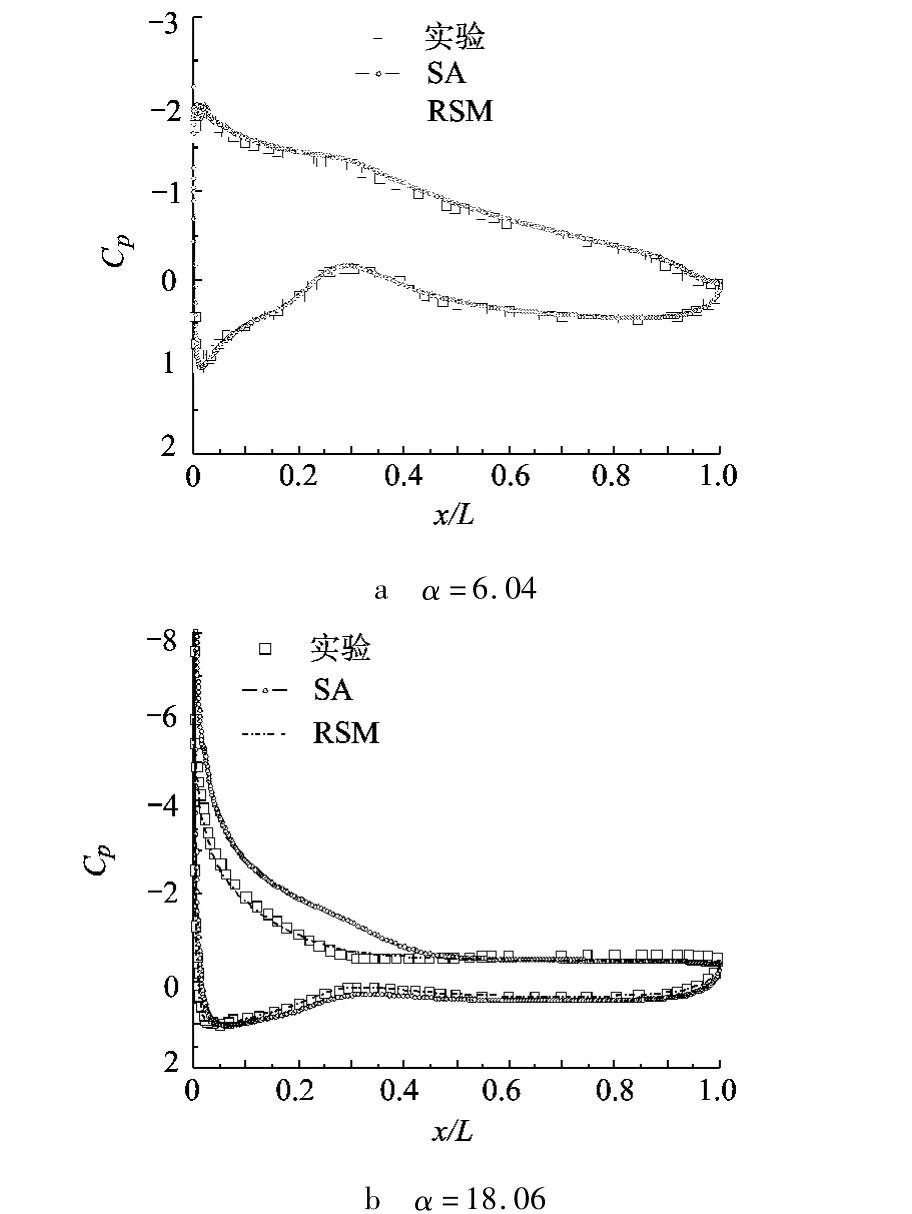
图4 压力系数
由图5流线图的比较可知,SA模型预测分离较晚,分离区域小于实际分离区,说明原始SA模型在流动发生分离后不能合理模拟出实际流场信息,有必要按照上节分析的思路修改Cb1值.
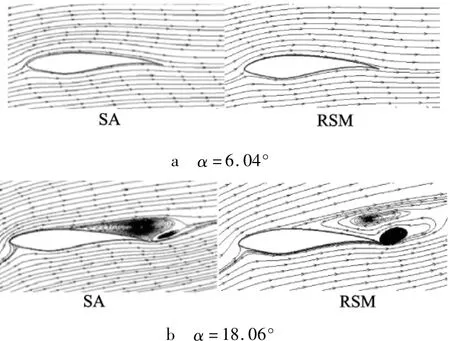
图5 流线图
3.2 SA模型改进结果分析
如上所述,在流动出现大范围分离的情况下,湍流处于强非平衡状态;随着攻角的变化,非平衡的程度也发生变化.本文对S825翼型在各攻角下选取不同参数的Cb1,对照实验结果进行了数值模拟.图6给出了Cb1随攻角变化的规律.图7为改进前后SA模型模拟得到的翼型升力系数,结果表明采用随攻角变化的Cb1才能得到与实验结果相吻合的翼型升力系数分布.
下文选取 12.08°,18.06°攻角下的流场,通过各方面的数值分析来比较改进前后的SA模型对于分离预估能力的差异.这两个工况下Cb1的取值分别为0.0754,0.080时,得到的结果与实验结果最为相近.
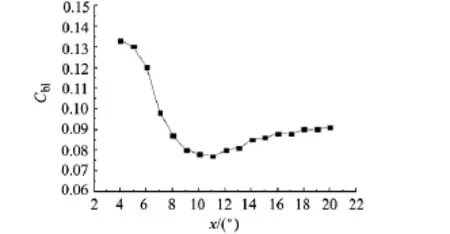
图6 Cb1与攻角的关系

图7 SA模型改进前后升力系数
1)平均流场对比分析.从图8可知12.08°,18.06°攻角下,原始SA模型从前缘到尾缘对吸力面的压力分布的预估都存在较大的偏差,改进后SA模型(MSA)吸力面上的分离点较原始SA模型提前,压力系数的分布得到修正,与实验结果基本一致.从图9可知改进后SA模型模拟流动分离区增大,更接近物理实际.可以认为,在大攻角工况下改进后SA模型对于分离的预估能力提高显著,模拟结果更接近于实际情况.

图8 SA模型改进前后翼型表面压力系数
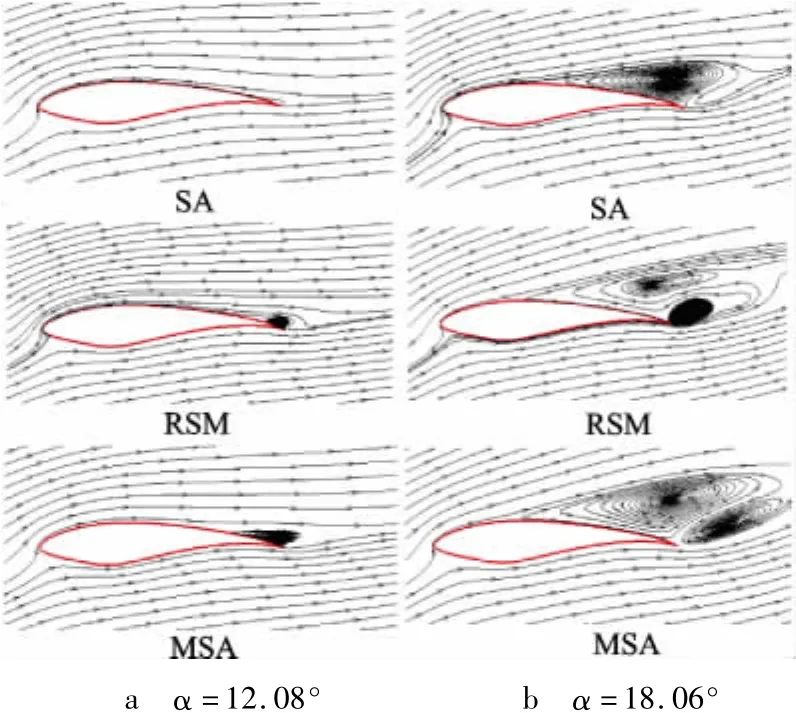
图9 SA模型改进前后流线
2)湍流输运特性对比分析.图10为12.08°,18.06°攻角下修正前后SA模型湍流粘性分布并与RSM模型所得的结果进行对比.由图可知原始SA模型模拟的湍流粘性偏小,减小Cb1后湍流粘性增加,使SA模型模拟所得结果与RSM模型模拟结果更加接近.
图11 给出了12.08°,18.06°攻角工况下湍流粘性的生成项Gν和耗散项Yν对输运过程的不同贡献.

图10 SA模型改进前后湍流粘性分布

图11 修正前(左)后(右)湍流粘性生成项、耗散项及生成耗散差值分布对比
从图11可以看到,随着攻角增大,流场内湍流活动增强,原始SA模型预估的湍流粘性生成偏高、耗散偏低,由此得出的流场内湍流的非平衡程度偏高.改进后SA模型由于模拟的分离区增大,预估的湍流粘性生成和耗散的范围相应扩大,但是在尾缘处生成项Gν有所减小.从图11湍流粘性生成项耗散项之差可以看出改进后SA模型得到的非平衡程度较原始SA模型降低.与上文表面压力系数及流线计算结果对比可以看到,原始SA模型过大地预估了湍流的非平衡程度,导致其对分离的模拟出现较大的偏差.
4 结论
通过CFD软件Fluent对美国NREL带有实验结果的风力机翼型S825进行数值模拟研究,对比分析了不同网格、不同湍流模型对翼型升力系数、压力系数分布和流场细节的影响.主要针对SA模型,基于非平衡湍流的特性以及湍流输运过程的分析,对其进行改进以提高模型在大攻角工况下对流场的模拟能力,主要结论如下:
由于二维翼型流动在大攻角下出现严重分离,湍流输运处于强非平衡态,其程度随攻角的变化而变化,因此在SA湍流模型中采用了随攻角变化的系数Cb1,改进后的模型能够合理地模拟出不同攻角下湍流粘性生成项Gν和耗散项Yν对湍流输运的影响,得到的升力系数、压力系数等流场信息与实验结果吻合得很好.本文对SA模型研究仅基于在S825单个翼型上进行,因此得到的对参数Cb1修改的规律还不具备普适性,但这一方法值得在以后的工作中进一步研究和完善.
References)
[1]刘磊,黄典贵,徐建中.湍流模型对风力机叶片气动性能预估的影响[J].工程热物理,2009,30(7):156 -161 Liu Lei,Huang Diangui,Xu Jianzhong.The impact of turbulence model for aerodynamic performance estimates of airfoil[J].Journal of Engineering Thermophysics,2009,30(7):156 - 161(in Chinese)
[2]马林静,陈江.风力机翼型气动特性数值模拟[J].太阳能学报,2010,31(2):45 -50 Ma Linjing,Chen Jiang.Numerical simulation foraerodynamic characteristics of airfoil[J].Acta Energiae Solaris Sinica,2010,31(2):45-50(in Chinese)
[3]Somers D M.Design and experimental results for the S825 airfoil[R].NREL/SR-500-36346,2005
[4]任年鑫,欧进萍.大型风力机二维翼型气动性能数值模拟[J].太阳能学报,2009,30(8):1087 -1091 Ren Nianxin,Ou Jinping.Numerical simulation 2D large-scale wind turbine airfoil aerodynamic performance[J].Acta Energiae Solaris Sinica,2009,30(8):1087 -1091(in Chinese)
[5]Spalart P R,Allmaras S R.A one-equation turbulence model for aerodynamic flows[R].AIAA Paper 92-0439,1992
[6]Lu L P,Wang D H,Liu Y W.Modification of S-A model for predicting corner separation flows in axial compressor[R].ACFD0149-T008-A-001,2010

