基于多重分形参数的高光谱数据特征提取

赵慧洁 蔡 辉 李 娜

(北京航空航天大学精密光机电一体化技术教育部重点实验室，北京100191)

高光谱遥感数据具有图谱合一的特点，提供丰富信息的同时波段之间具有较强的相互性和冗余性，降低了数据处理的效率，甚至精度.特征提取为上述问题提供了有效的技术手段.高光谱数据特征提取方法主要包括基于光谱特征参量提取、基于数学变换以及基于光谱空间子集的方法，特征参量提取的方法仅仅考虑了光谱局部吸收特征，光谱子集方法不改变光谱物理特性但会造成数据细节信息的缺失，基于数学变换方法可以从统计、物理、波形变化趋势等方面实现光谱特征提取;为了提取稳定的光谱特征，如何有效地综合利用光谱局部吸收特征以及光谱波形幅值与变化趋势是特征提取的热点研究方向.因此，针对上述问题，本文将分形理论引入到高光谱数据光谱特征提取，从反射波谱的形成过程来看，光谱曲线不仅具有自相似性而且具有一定的奇异性，其具有某种分形体的特征.

分形理论是非线性科学的一个重要的分支，在遥感应用中，常常被用来研究遥感影像的空间分形特征［1－3］，近年国内外开始针对光谱曲线进行分形特征分析，但是仅限于Hausdorff维数、关联维数在光谱识别中的应用研究［4－5］，分形维数不能有效表征高光谱数据稳定的光谱特征以及局部细节光谱特征，因此，本文引入多重分形的理论，多重分形谱是描述多标度复合分形生长形成的复杂体系，它定量的刻画了分形子集上的具有不同标度和标度指数的分形子集的局部标度性，光谱曲线是具有多重分形特征的复杂信号.理论上多重分形谱具有无限高维数，实际应用中采用估计方法得到的多重分形谱维数一般在50以上才能代表信号包含奇异性对应的分形维数分布.为了将多重分形理论应用到高光谱图像处理中，有必要从分形谱中提取一组包含多重分形谱大部分信息的参数［6］，作为光谱特征参数，为进一步分类、识别等应用提供良好的基础.针对高光谱数据的特点与应用需求以及如何有效表征多重分形谱参数等问题，提出了基于光谱概率测度的多重分形谱参数光谱特征提取方法，并应用于高光谱数据监督分类中，有效地提高地物分类精度，验证了特征提取参数的有效性和可靠性.

1 光谱曲线多重分形谱及参数提取

多重分形谱f(α)是一个以Holder指数α为自变量的函数，其函数值可以理解为过程在时间［0，T］内随机抽取的时刻，具有给定Holder指数α的概率.

1.1 多重分形谱计算方法

为了实现多重分形谱提取引入光谱概率测度以及配分函数等方法实现多重分形谱的计算:利用光谱信息度量 (SIM，Spectral Information Measurement)［7］的方法计算出光谱概率测度 P(δ)，采用文献［8］提出的配分函数法，通过勒让德Legendre变换计算多重分形谱.

1)光谱概率测度计算.对于高光谱数据某一地物光谱曲线，沿波长方向划分为尺寸为δ的N(δ)个一维小盒子，Si(δ)表示尺寸为δ的第i个小盒子内所有光谱波段的辐亮度/反射率值之和，则i个小盒子内光谱曲线的概率测度表示为

2)配分函数构造.光谱曲线的配分函数［9］χq(δ)为

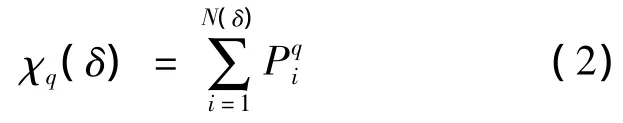
其中，q为权重因子.

3)尺度函数估计.在无标度的自相似区域内χq(δ)与δ之间存在的幂率关系:

log2χq(δi)作为 log2δi的函数拟合得到尺度函数τ(q):

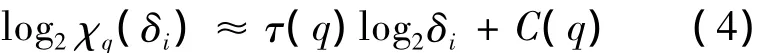
4)多重分形谱和Holder指数计算.式(4)利用尺度指数τ(q)测量了χq(δ)随权重因子q的渐近衰减性.尺度指数、Holder指数和多重分形谱满足Legendre变换:

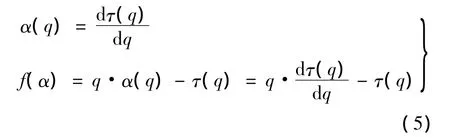
f(α)是描述多重分形子集维数的连续谱，如果研究对象是单分形的，则f(α)为一定值;如果研究对象是多分形的，则f(α)为单峰曲线.

1.2 多重分形谱参数

不同地物具有不同的分形谱曲线，根据多重分形谱可以进行地物的分类与识别.由于高光谱数据提供空间信息的同时提供了连续的光谱曲线，因此，为了将多重分形理论应用于高光谱图像分类、识别等应用，需从多重分形谱中提取一组表征多重分形谱特征的参数［6］.

多重分形谱包含Holder指数 α和分形谱f(α)两个参量，为了使提取的参数能够有效地表征多重分形谱，参数包含了表征多重分形谱形态的具有特殊性质的点，一般情况下多重分形谱为一单峰曲线［10］，因此，本文选择多重分形谱的对称轴、横坐标极大与极小点以及极小点对应的分形维数作为特征参数，如表1所示.

表1 多重分形谱参数及其表达式

αmin和αmax表示给定q条件下概率奇异性的最小值和最大值，度量了整个奇异性分布的宽度;α*为多重分形谱f(α)最大值点对应的Holder指数，反映了分形谱的对称性;f(αmin)为光谱曲线上Holder指数取最小值的波段子集分形维数.f(αmin)和f(αmax)分别对应于 q＞0和 q＜0的分形维数，f(αmin)描述的是大波动特征，f(αmax)描述的是小波动特征，光谱曲线的峰和谷特征为大波动特征，要准确的度量光谱特征应该选用f(αmin).f(αmax)描述的小波动特征放大了噪声及其它带来小误差的因素的影响，抑制了峰谷特征，因而不能用作特征参数.利用PHI(Prush-broom Hyperspectral Imager)数据某地物光谱曲线(如图1a)进行多重分形谱及其参数描述(如图1b).

图1 PHI数据地物光谱及其多重分形谱参数

2 实验结果与分析

航空高光谱成像光谱仪PHI(光谱分辨率5～10 nm，波长范围 400～850 nm，瞬时视场角1.0 mrad，信噪比大于200)获得的江苏方麓茶场航空数据进行实验，验证本文方法的性能.为了验证特征提取性能(可分性与所含信息量等)，实验中以最小欧氏距离(MED，Minimum Euclidear Distance)作为分类准则，应用数据大小为210×150×64.地物类型标识与采用的测试样本如表2所示.

表2 各类别地物标识与测试样本

各类别的多重分形谱参数如表3.以信息量维数(FDI，Fractal Dimension of Information)、多重分形谱(MFS，Multi-Fractal Spectrum)和多重分形谱参数(MFSP，Multi-Fractal Spectral Parameters)为特征，采用MED进行监督分类，结果统计参数如表4所示，分类精度比较如图2所示.

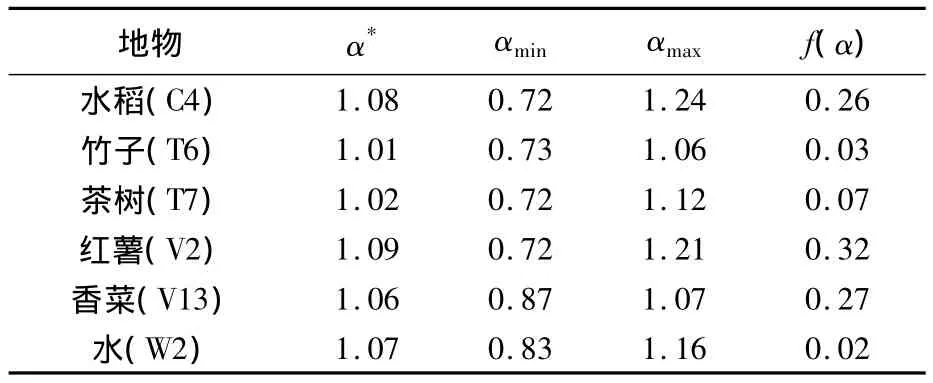
表3 参考光谱多重分形参数

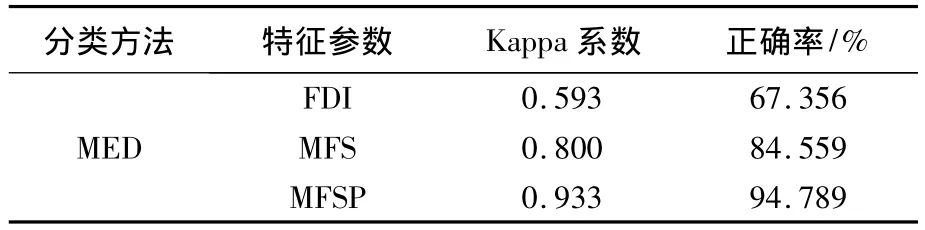
表4 分类结果统计

从图3可以看出，当地物光谱特征能够显著区别于其它地物时，单一分形维数也能够取得较好的分类效果，如FDI对红薯的分类正确率达94%;当地物光谱较为相似时，MFS和MFSP的优越性更加明显，图3中MFS，MFSP的分类精度明显高于FDI;MFS，MFSP的总体分类精度分别达84%和94%以上，显著高于 FDI的67.356%.Kappa系数体现分类结果的一致性，表3结果显示，MFSP分类的Kappa系数达0.933，说明每个单一类别的分类正确率都高，分类结果的一致性高.

利用MFS，MFSP特征进行MED的分类结果如图3所示.图3a、图3b中红薯、水稻、香菜、水体均得到了较好的分类结果;由于竹子和茶树分布混合较多且光谱接近，图3a中的错分现象较图3b明显.

图2 各地物分类精度

图3 MFS和MFSP监督分类结果图比较

3 结论

本文提出的基于光谱概率测度的多重分形谱参数特征提取方法，利用表征多重分形谱的形态参量，有效地结合了α～f(α)包含的光谱曲线奇异性特征和分形特征，放大了光谱较大的波动特征(吸收特征)，充分考虑了高光谱数据局部吸收特征，增加了具有相似光谱地物之间的可分性.将本文方法应用于PHI数据地物分类，实验结果证明:利用本文方法提取的特征进行监督分类获得了94.789%的总体分类精度，并有效地提高了易错分地物之间的分类精度.

References)

［1］Zhou Ziyong.Multifractal based hyperion hyperspectral data mining［C］//The Seventh International Conference on Fuzzy System and Knowledge Discovery.USA，NJ:IEEE，2010:2109 －2113

［2］Tzeng Y C，Fan K T，Su Y J，et.al.A parallel differential box counting algorithm applied to hyperspectral image classification［C］//IEEE International Geosciences and Remote Sensing Symposium(IGARSS).USA，NJ:IEEE，2009:V216 － V219

［3］张峰，邹焕新，雷琳.一种基于局部分形维的CFAR检测算法［J］.信号处理，2012，28(1):205 －211 Zhang Feng，Zou Huanxin，Lei Lin.A CFAR detection algorithm based on local fractal dimension［J］.Signal Processing，2012，28(1):205－211(in Chinese)

［4］Zhang Huaguo，Huang Weigen，Zhou Changbao.Fractal characterization of IKONOS imagery［C］//Multispectral and Hyperspectral Remote Sensing Instruments and Applications.Bellinggham:SPIE，2003，4897:292 －301

［5］周子勇，李朝阳.高光谱遥感数据光谱曲线分形特征研究［J］.中北大学学报，2005，26(6):451 －454 Zhou Ziyong，Li Chaoyang.Fractal feature of hyperspectral remote sensing spectral curves［J］.Journal of North China Institute of Technology，2005，26(6):451 －454(in Chinese)

［6］Abadi M，Grandchamp E.Legendre spectrum for texture classification［C］//The 8th International Conference on Signal Processing.USA，NJ:IEEE，2006，2:16 －20

［7］Chang Chein I.Spectral information divergence for hyperspectral image analysis［C］//IEEE International Geosciences and Remote Sensing Symposium(IGARSS).USA，NJ:IEEE，1999，1:509－511

［8］Halsey T C，Jensen M H，Kadanoff L P，et al.Fractal measures and their singularities:the characterization of strange sets［J］.Physical Review A，1986，33(2):1141 －1151

［9］周炜星，王延杰，于遵宏.多重分形奇异谱的几何特性Ⅱ.配分函数法［J］.华东理工大学学报，2000，26(4):390 －395 Zhou Weixing，Wang Yanjie，Yu Zunhong.Geometrical characteristics of singularity spectral of multifractalⅡPartion function definition［J］.Journal of East China University of Science and Technology，2000，26(4):390 －395(in Chinese)

［10］李彤，商朋见.多重分形在掌纹识别中的研究［J］.物理学报，2007，56(8):4393 －4400 Li Tong，Shang Pengjian.A multifractal approach to palmprint recognition［J］.Acta Physica Sinica，2007，56(8):4393 －4400(in Chinese)