混沌微粒群算法在离散型生产调度中的应用

陈宇航，刘阶萍，秦智晗

（北京交通大学机械与电子控制工程学院，北京100044）

生产调度问题属于NP-hard问题，是一种很难解决的理论难题。为了有效地解决生产调度问题，研究人员往往需要对复杂的问题进行理论分析，建立数学模型以求解不同的生产调度问题。但通过这类方法很难找到最优解，效果不理想。近年来，人们运用仿生型智能优化算法求解生产调度问题，如遗传算法、模拟退火算法、蚁群算法、微粒群算法等。

在生产调度领域，因为微粒群算法的概念简明、依赖的经验参数较少、收敛速度快、实现方便，所以短期内得到了一定的发展与应用，尤其是在离散型生产调度优化方法研究方面的应用越来越多[1~2]。但是微粒群算法容易陷入局部最优解、后期收敛速度慢，本文基于此对微粒群算法提出改进，在离散型生产调度优化中采用实际项目算例进行验证[3~4]，在算法运行后期加快了群体的收敛速度，避免了容易陷入局部最优的缺陷，使目标问题的解更加接近最优解，提高了解的质量。

1 数学模型

离散型调度问题，也被称为非流水车间调度问题[5]，该问题研究n个任务在m台机器上作业，已知各工序的作业时间和各工件的加工次序，而假设所有工件的工艺顺序不完全相同。离散型调度的问题一般有：火箭、飞机、船舶、武器装备、机械、玩具生产等行业[6]。对于此类问题，通常假定[7~8]：

（1）一个任务在同一时刻只能在一台机器上加工；（2）每台机器在同一时刻只能加工一个任务；（3）任务的加工时间在初始时确定，且在整个加工过程中保持不变；（4）任务的加工准备时间和运输与顺序无关，且包含在加工时中；（5）每台机器上加工各任务的顺序不完全一样；（6）每个任务在所有机器上的加工顺序是不完全一样。

此类问题一般需要满足以下2个约束条件：

（1）机器约束：每台机器在同一时刻只能加工一个任务；（2）工艺约束：每道工序必须在它前置的工序加工完毕后再进入下一道加工。

离散型调度问题流程如图1。将这一类问题的数学模型归纳如下[7]：

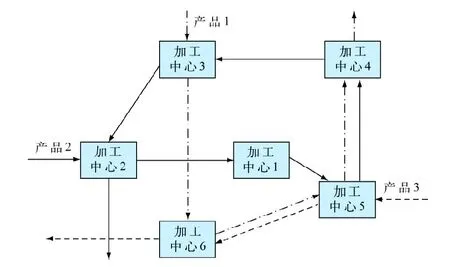
图1 离散型调度问题流程图

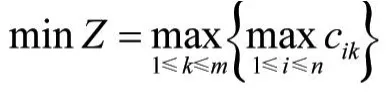
S.T.

cik－pik+M(1－aihk)≥cih，

i=1,2,…, n；h, k=1,2,…, m

cjk－cik+M(1－xijk)≥pik，

i,j=1,2,…, n；k=1,2,…, m

cik≥0, i=1,2,…, n；k=1,2,…, m

生产调度的目标即为产生一个优化的工件调度序列，使得最大流程时间尽可能的小。

2 基于混沌的微粒群算法

微粒群算法，又称粒子群优化(Particle Swarm Optimization,PSO)，是一种演化计算技术，来源于对一个简化社会模型的模拟[9]。该算法在图像处理、模式识别和多目标优化等领域得到广泛应用。

微粒群算法后期容易陷入局部最优解且收敛速度慢，本文提出了基于混沌的微粒群算法（Chaotic Particle Swarm Optimization,CPSO）来求解复杂的调度离散问题[10]。利用混沌的遍历性特点进行优化搜索且能避免陷入局部极小，因此，混沌优化搜索方法已成为一种新颖的优化技术[11~12]，将该技术嵌入到微粒群算法，增强其功能。

混沌微粒群算法的优化过程如下[13]：

（1）将所有微粒（种群规模为N）进行初始化，在一定的范围内随机设置微粒的初始位置x和速度v，微粒群的进化代数genn。

（2）设定混沌搜索部分的参数。加速常数c1和c2；惯性权重wmin和wmax；混沌变量序列长度m；粒子飞行速度限制设置，该维的速度被限制为该维最大度vmax，即vid∈[-vmin,vmax] 。

（3）在一定的范围内随机产生微粒的初始位置和速度，令迭代次数k=1。

（4）根据下式计算惯性权重。

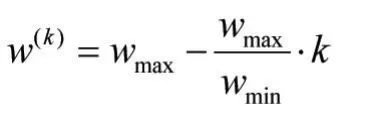
（5）对每个微粒，将它的适应值和它经历过的最好位置Pbest作比较，如果较好，则将其作为当前的最好位置Pbest；对每个微粒，将它的适应值和全局所经历最好位置Gbest作比较，如果较好，则将其作为全局的最优解。

为了使得到的结果不要超出所允许的范围，设定如果vk＜vmin，则vk=vmin；如果vk＞vmax，则vk=vmax；如果xk＜xmin，则xk=xmin；如果xk＞xmax，则xk=xmax。其中vmax和vmin为vk的取值范围；而xmax和xmin为xk的取值范围。

（6）在区间（0,1）内任取值rand（0,1），根据公式（1-6）计算Pk，比较rand（0,1）与Pk的大小，如果rand(0,1)≤Pk，则根据以下步骤进行混沌搜索，否则转到步骤（7）。

采用混沌搜索的概率计算公式：

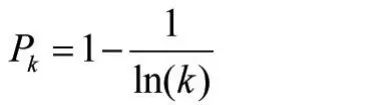
其中k为迭代的次数。在算法初始，P值较小，整个程序以微粒群算法为主，以很小的概率调用混沌搜索，可以更好地保证搜索的速度。随着迭代次数的增加，k值增大，即P值越来越趋近于1，算法以更大的概率采取混沌搜索。这主要是因为在算法搜索的初期，微粒群算法搜索速度快，且具有很好的收敛性，采用微粒群算法就可以获得较好的搜索效果，但是随着搜索的进行，到进化后期，微粒群搜索收敛性越来越慢，因而采用混沌搜索来弥补这一弱点。因此，在整个搜索寻优的过程中既充分发挥了微粒子群算法简单易实现、搜索速度快的优点，又在进化后期有效地改进了微粒群算法，使得最后不会收敛到局部最优值。

下面介绍混沌搜索的具体过程：

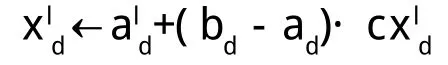
c.对xld进行混沌搜索：

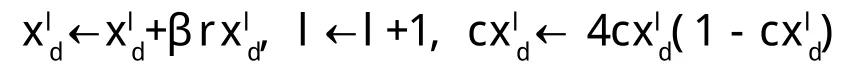
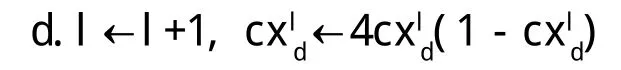
e.重复b、c、d步骤，直到一定步数内f*保持不变或达到给定的最大搜索步数，结束寻优计算，此时的即为算法得到的最优变量，f*为得到的最优解。

（7）计算适应度，确定全局最优值。

（8）按照速度和位置更新方程(1-1)更新微粒的速度和位置。

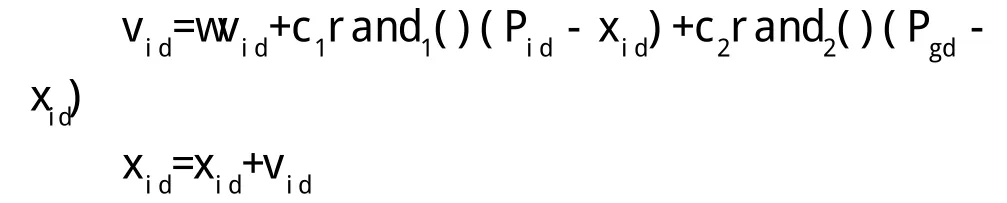
（9）如果还没有达到结束条件（通常为足够好的适应值或达到一个预设最大代数），令k=k+1则转步骤（4）。如果达到条件，则输出全局最优值，程序结束。

混沌微粒群算法流程如图2。

3 算例分析

3.1 项目背景

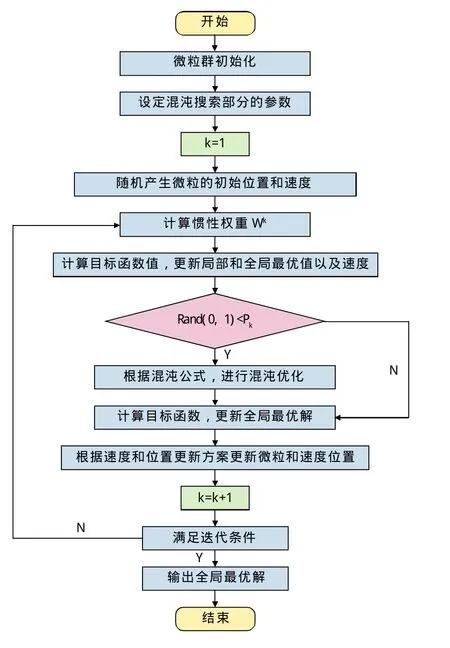
图2 混沌微粒群算法流程图

某航空发动机公司的精密件加工任务主要由某机械厂车间承担。试验车间布置和工件流动场景如图3。精密件加工属于典型的离散制造。

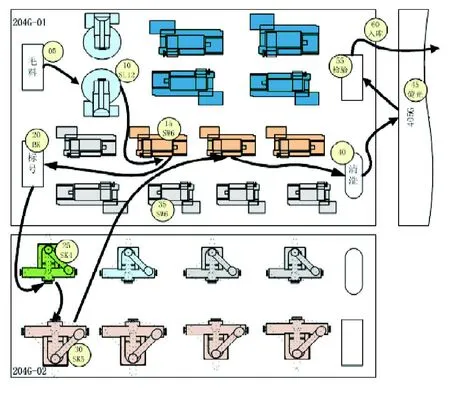
图3 试验的车间布置和工件流动场景图

然而，在加工现场每类设备只有一台，其他设备留作意外情况发生时（比如机器故障、生产任务增加等）使用，以保障整个生产任务的正常进行并完成。

在该车间，精密件整个加工制造流程主要包括生产任务接收、生产准备、工艺执行、产品检验和产品交付5个环节。

3.2 编码方式

工厂的生产任务是根据生产计划下发的订单分解后下达到各个车间。本次的研究基于某个项目的具体事例进行分析。其订单包括5种类型的工件，根据以往的生产经验，调研并采集数据，将得到每道工序的平均加工时间以及每道工序对应的时间如表1。

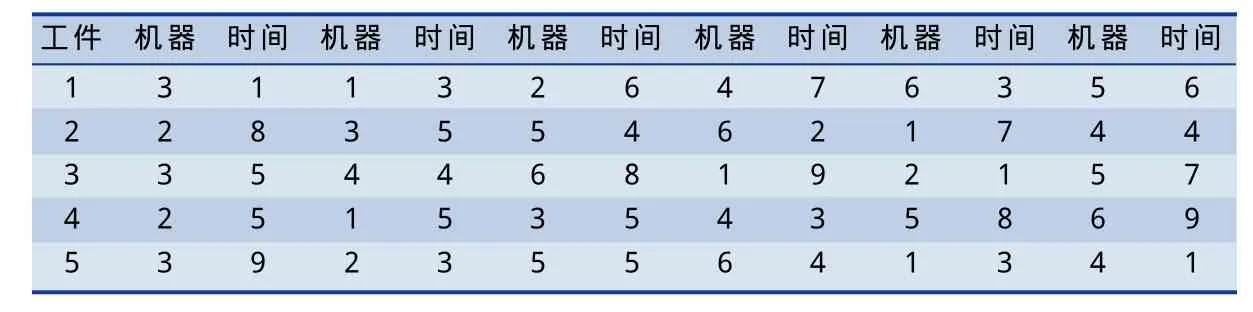
表1 项目某订单作业时间表

对于n个任务m台机器流程型生产调度，每个任务都要按照一定顺序在m台机器进行作业，因此，n个任务就有n×m道工序。采用基于工序的染色体编码方式[7]，用自然数1,2,…, n表示每个任务，相同任务的不同工序均用同一个任务号表示，每个染色体包括n×m个代表工序的基因，从而形成所有任务的工序排列，其中每个任务m次出现在染色体中，每个基因只有上下依赖关系的工序。染色体的任意排列总能产生可行调度。解码过程是先把染色体转化为一个有序的工序表，然后根据工序表和生产任务的工艺约束，以最早允许作业时间对各任务逐个进行加工，从而得到调度方案。在编程过程中，设置w=3（程序运行次数），genn=50（最大代数），PS=50（种群规模），e=0.4（PSO算法惯性因子），针对这5种类型的工件，分别采用PSO、CPSO得到不同的生产调度结果。

3.3 CPSO算法结果

基于PSO与CPSO的适应度收敛曲线如图4。由图可以看出，在前期，采用CPSO得到的收敛速度与PSO的几乎相同。但是，在搜索后期采用CPSO收敛速度更快。而且CPSO得到的目标值比PSO得到的结果好，这表明了CPSO弥补了PSO在后期容易陷入局部最优解及收敛速度慢的特点。基于CPSO的精密件加工作业甘特图如图5。结果如下：

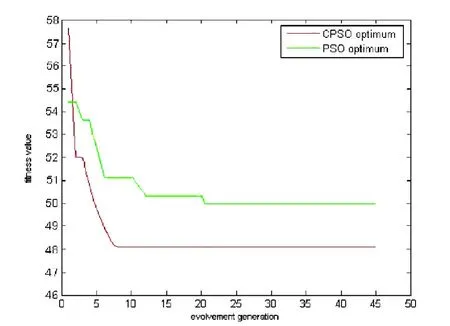
图4 基于PSO与CPSO的适应度收敛曲线

minm=48

BestPosition=

机器1：J1→J4→J3→J5→J2；

机器2：J4→J1→J5→J2→J3；

机器3：J1→J3→J5→J4→J2；

机器4：J3→J1→J4→J5→J2；

机器5：J5→J4→J2→J1→J3；

机器6：J3→J1→J5→J2→J4

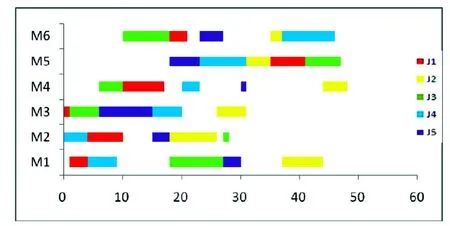
图5 基于CPSO的精密件加工作业甘特图

经过计算得到基于CPSO的精密件加工的机器利用率分别为：M1：56.25%；M2：45.83%；M3：52.08%；M4：39.58%；M5：60.42%：M6：4.17%。用PSO与CPSO得出来的机器利用率对比如图6，采用CPSO方法得到的机器利用率明显增高。

4 结束语

对于离散型生产调度组合优化问题，微粒群算法的改进对于目标解的寻找有着较大的帮助。基于混沌微粒群算法搜索速度较快，有助于调度工作效率的提高。在未来的研究中，可以充分利用基于混沌微粒群算法的优势，将其应用于静态和动态的生产调度领域，还可以用于流程型生产调度、混合流程型生产调度等领域。

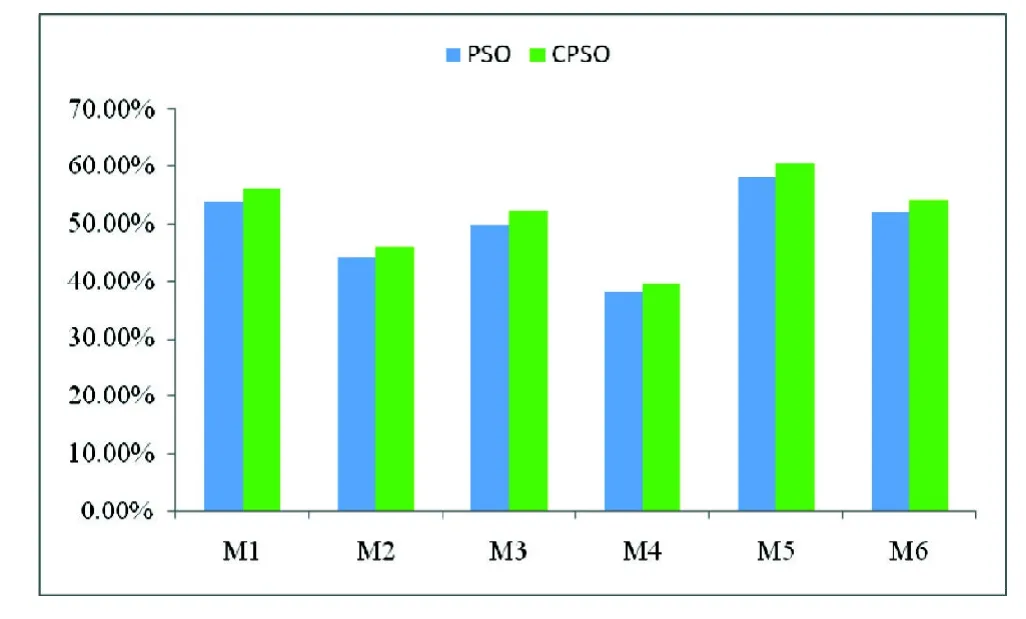
图6 基于PSO与CPSO的机器利用率对比

[1] 王凌，刘波. 微粒群优化与调度算法[M] . 北京：清华大学出版社，2008.

[2] Lawler,Lenstra,Rinnooy Kan,Sequecing and Scheduling: Algorithms and Conplexity[J] .Operations Research and Management Science,Vol.4.

[3] 高立群，任苹，李楠. 基于混沌粒子群算法的高速旅客列车优化调度[J] . 东北大学学报，2007（2）.

[4] 吴月秋，纪昌明，王丽萍，李志胜. 基于混沌粒子群算法的水电站水库优化调度[J] . 人民黄河，2008，30（11）.

[5] 唐宇. 基于微粒群算法的车间调度问题研究[D] . 杭州：浙江工业大学，2007.

[6] 苏成利，徐志成，王树青. PSO算法在非线性系统模型参数估计中的应用[J] . 信息与控制，2005，34（1）：123-125.

[7] 顾擎明，宋文忠. 混合遗传算法在Job-shop调度问题中的应用[J] . 信息与控制，1998，27（5）：369.

[8] ChengR.GenM.A Tutorial Survey of Job Shop Scheduling Problems Using Genetic Algorithms Representation[J] . Computers& Industrial Engineering. 1996, 30(4): 983-989.

[9] 崔志华，曾建潮.微粒群优化算法[M] . 北京：科学出版社，2011.

[10] 曹蕴. 基于混沌搜索与粒子群算法的配电网规划的研究[D] . 北京：华北电力大学，2008

[11] 石欣. 基于混沌粒子群算法的同步发电机最优调速控制系统[D] . 天津：天津大学，2007.

[12] Lovbjerg,Rasmussen. Hybrid:Partical Swarm Optimizer With Breeding and subpopulation[C] .In:Proc of the third Genetic and Evolution Compution Conference,2001