灰色动态模型群在城市轨道交通客流预测中的应用研究

曹鸿飞，张 铭，李 平

（中国铁道科学研究院电子计算技术研究所，北京100081）

在城市轨道交通的规划、设计、建设及运营等环节中，客流预测作为一项基础工作，它的准确性直接关系到城市轨道交通的建设投资和运营效率。

城市轨道交通是一个复杂的系统，受自然、社会、经济以及文化等各种因素的综合影响，其客流预测难以采用常规的确定性模型进行预测。由于影响其客流的诸多因素具有不确定性，可以基于历史客流数据建立灰色系统模型。该模型适用于参数信息不完全、概念内涵不确定、运行机理不明确的系统，仅从复杂的数据中找规律，在建模时对实验观测数据及其分布没有特殊的要求和限制[1]。因此可通过运营中积累的历史数据，对客流的未来状态进行科学的定量预测。目前基于灰色系统理论的客流预测方法主要有灰色GM(1, 1)预测和灰色马尔可夫预测。前者适用于具有明显指数规律的序列，只能描述单调的变化过程。后者则难以在应用中进行合理的状态划分[4]。鉴于城市轨道交通客流分布呈现出非单调的摆动发展序列，采用Verhulst模型更为合适。本文选取了某城市轨道交通线路10天的日客流量数据，发现呈非单调摆动形变化趋势，故采用Verhulst模型对第11天的客流进行预测。

1 灰色Verhulst模型

根据文献[2] ，Verhulst 模型的基本原理和计算方法如下：

定义1 ： 设X(0)为原始数据序列

X(0)=(x(0)(1), x(0)(2), …, x(0)(n))

X(1)为 X(0)的一次累加生成（1-AGO）序列

X(1)=(x(1)(1), x(1)(2), …, x(1)(n))(K=1, 2, …, n)

Z(1)为 X(1)的紧邻均值生成序列

Z(1)=(z(1)(2), z(1)(3), …, z(1)(n))

Z(1)(k)=0.5(x(1)(k)－x(1)(k－1))(k=2,3,…,n)

则称

X(0)+aZ(1)=b(Z(1))2

为灰色 Verhulst 模型，a和b为参数。称

为灰色Verhulst模型的白化方程，t为时间。

定理1 ：设灰色 Verhulst 模型如上所述，若a＾=[a,b]T

为参数列，且

则参数列a＾ 的最小二乘估计满足

a＾=[BTB]-1BTY

定理2 ：设灰色 Verhulst 模型如上所述，则其白化方程的解（时间响应函数）为

故，灰色 Verhulst 模型的时间响应序列为

可以将X(1)(0) 取为 X(0)(1)，则上式变为

对上式做累减还原，则原始数据序列的灰色Verhulst 预测结果为：

2 灰色动态模型群的建立

相应地受到影响。一般而言时间上越旧的数据预测意义越弱，不断补充新数据才能反映系统当前的最新特征。尤其是系统随着量变的积累，发生质的飞跃或突变时，应该及时去掉已经无法反映系统当前特征的旧数据[2]。

实际建立灰色模型时，选择不同的数据，模型参数a, b的值都是不一样的。由此反映出不同条件对系统特征的影响。灰色系统模型的建立一般要求原始数据的数目不少于4个。假设原始数据序列为{ X(0)(1), X(0)(2),…， X(0)(n)}，那么含有最后一个数据的序列有n-3个，则可以建立由 n-3个Verhulst模型组成的灰色模型群。

以 {X(0)(n－3), X(0)(n－2), X(0)(n－1),X(0)(n)}建立的第1个模型为：

以 {X(0)(1), X(0)(2),…， X(0)(n)} 建立的第n-3个模型为：

使用模型群进行分别预测后，取不同的预测值的算术平均值：

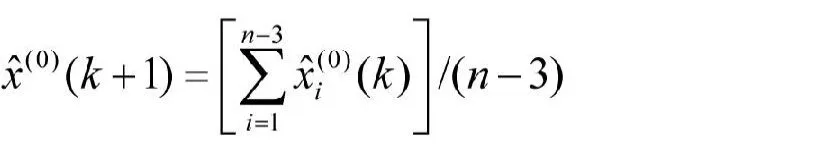
最后再做累减还原，则最终的灰色动态模型群预测结果为：

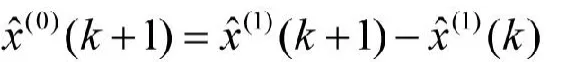
3 轨道交通客流预测实例

以某城市轨道交通线路的日客流数据作为样本，采用基于灰色系统理论的预测模型进行研究，数据统计见表1和图1。

由于该城市经济发达、交通便利、人口相对较少、私家车拥有量较高，故一般工作日乘坐轨道交通出行的客流人数较少。从图1中可以看出，10日内的客流数据序列呈现出非单调波动性，周二至周四客流量相对较少，周五至周一则出现明显增加。客流数据真实反映了该城市的社会经济特征。图2为实际客流数据曲线、一次累加生成序列和二次累加生成序列的曲线图。

在灰色系统的建立过程中，许多新的随机扰动或驱动因素会不断地进入系统，使系统的发展

表1 日客流数据统计表

由图2可知，经过两次累加生成后，序列呈指数级增长特点，故可以采用灰色理论进行研究。

（1）GM(1,1)模型

以10天的客流数据为基础，建立由7个灰色GM(1,1)模型组成的模型群，用于对2011年5月1日客流数据的预测。表2和图3为预测结果和误差曲线。

图1 日客流数据统计图

图2 数据序列对比

灰色预测一般忽略所有外界因素影响，仅从数据序列中寻找规律进行预测。同时，由于GM(1,1)模型一般适用于具有指数级增长的序列，不能很好的把握数据序列的周期性，所以该方法的预测结果不具有较高的预测精度。

（2）灰色Verhulst模型

由于Verhulst预测模型适用于呈S形序列的预测，以2011年4月21日~30日客流数据为样本，建立模型数量为7的灰色Verhulst预测模型群，对2011年5月1日的客流进行预测。表3和图4为预测结果和误差曲线。

表2 灰色GM（1,1）模型群预测结果

图3 灰色GM（1,1）模型预测误差曲线

表3 灰色Verhulst模型群预测结果

图4 灰色Verhulst模型群预测误差曲线

由预测结果可以看出，当取7天的数据进行预测时，预测误差较大，是因为城市轨道交通客流以“周”为周期，当恰好取一周的数据进行预测时，不能反映出其周期性的规律。当取10天的客流进行预测时，预测误差则显著降低。

在实际工程应用中，选取客流数据的预测样本时应遵循以下原则：（1）选取预测日前8~12天的数据作为样本，使模型能更好地反映城市轨道交通客流的周期性特点；（2）对模型群的预测结果做算术平均后作为实际预测结果，避免单个模型预测结果的缺陷，使预测结果更精确、更可靠。

4 结束语

本文在Verhulst模型和灰色动态模型群的基础上，针对轨道交通客流数据的周期性特点提出了一种组合预测模型。该方法在合理选择预测样本的前提下，可以有效提高短期预测的精度。实例计算证明了该方法的精确性和可靠性。

通过将本文提出的方法，应用于城市轨道交通客流的预测，在异常客流发生前进行预警，可以供相关人员参考以便采取相应措施防患于未然，为城市轨道交通运营安全提供可靠保证。

[1] 邓聚龙. 灰理论基础[M] .武汉：华中科技大学出版社，2002.

[2] 刘思峰，党耀国，方志耕，谢乃明. 灰色系统理论及其应用[M] . 北京：科学出版社，2010.

[3] 王韶伟，许新宜，贾香香，徐劲草. 基于灰色动态模型群的需水预测研究[J] . 中国农村水利水电， 2010（2）： 29-31.

[4] 石树新，王花兰. 城市货运量的灰色Verhulst预测模型[J] .交通科技与经济， 2007（1）：88-90.

[5] 王奕，徐瑞华. 基于周期时变特点的城市轨道交通短期客流预测研究[J] . 城市轨道交通研究，2010（1）：46-49.

[6] 王富章，李平，刘德山. 城市轨道交通智能综合监控系统及关键技术[J] . 交通运输系统工程与信息，2004， 4（3）：24-28.