浙东水资源系统仿真模拟模型研究
吴文静,周 芬,王灵敏
(浙江省水利水电勘测设计院,浙江杭州 310002)
0 引言
浙东地区即萧(山)绍(兴)宁(波)舟(山)地区,区域面积14 664 km2,是长江三角洲经济区重要组成部分,在浙江省的经济发展中起着举足轻重的作用.
为解决浙东地区水资源匮乏问题,浙江省实施了全省目前涉及行政区域和流域最多、组成最复杂的浙东引水工程,这是确保浙东地区经济社会可持续发展的重大水资源配置工程,也是解决环杭州湾地区水资源平衡、合理调配水资源的重要组成部分.该工程通过萧山枢纽、曹娥江大闸枢纽、曹娥江至宁波引水工程、舟山大陆引水工程将富春江、曹娥江、甬江、萧绍宁河网等供水水源联通起来,形成分源配水、分质供水的水资源配置网络,以农业和一般工业作为主要供水对象,并兼顾改善河网的水环境,由西向东供水直至舟山群岛;并在曹娥江上游兴建水库,向整个浙东地区提供优质水和一般用水.
本文针对浙东引水工程实际情况和浙东地区水资源系统特点,通过水资源模拟系统概划,建立了浙东水资源系统仿真模拟数学模型,主要包括产汇流模拟、水量配置模拟和河网水动力模拟三个子模型,并利用该模型对浙东引水曹娥江至宁波引水工程曹娥江最低可引水水位进行方案比选.
1 浙东引水工程概况
浙东引水工程的主要任务是引富春江水向萧绍宁平原及舟山市补充工业和农灌等一般用水,并兼顾改善水环境.工程主要组成部分有:浙东引水萧山枢纽、浙东引水曹娥江大闸枢纽、浙东引水曹娥江至慈溪引水工程(北线)、浙东引水曹娥江至宁波引水工程(南线)、浙东引水舟山大陆引水工程、浙东引水钦寸水库等.
浙东引水工程是通过提供一般用水水量,将浙东供水区水库原用于供给农业和一般工业的水量置换出来用于生活用水,从而提高浙东地区优质用水户的供水保证率.工程供水受益范围为浦阳江以东、曹娥江曹娥下游的绍兴平原、姚江平原和舟山海岛.受益县市主要包括绍兴市的越城区、绍兴县、上虞市,宁波市的鄞州区、海曙区、江东区、江北区、北仑区、镇海区、余姚市、慈溪市、奉化市,舟山市的普陀区、定海区、金塘岛和岱山县.
2 浙东水资源系统的特点及概化
2.1 浙东水资源系统的特点
浙东水资源系统是由若干水利工程、水源地、供水区和容泄区等组成,这些区域又分属不同的流域、河区或行政区,其水文情况既相互独立又相互联系,种种因素决定浙东水资源系统是一个多因素多层次的相当复杂的系统,其主要特点有:
(1)跨行政区 从行政区划上分别属杭州市、绍兴市、宁波市和舟山市的多个县(市或区),平原河网在行政边界上均设有节制闸.
(2)跨流域 主要涉及到钱塘江流域、曹娥江流域和甬江流域,需要协调解决好防洪与供水之间、引水和冲淤之间的矛盾.
(3)多水源 水源工程有山区水库、平原河网、江道水库.区内有大中型水库29座,平原河网分别有萧绍平原河网、虞北平原河网、余姚河网、慈溪河网、宁波河网,江道水库有曹娥江大闸闸上水库、上浦闸闸上水库和姚江江道水库.
(4)多用户 用水户主要有城乡生活用水、工农业生产用水、生态环境用水、水闸冲淤用水和船闸用水等,各用水户对水量、水质和保证率均有不同要求.遭遇较大干旱年份时,首先保证居民生活和重要工业用水等优质用水户.
(5)河网多水级 引水地区地势由西向东从高逐渐降低,河网常水位也随之降低,平原内部按常水位分成多个河区,不同河区之间均以节制闸、滚水堰为界.
(6)供水工程多级串并联、且多级反馈 水库的弃水是河网的主要水源之一,而部分水库是从所在片河网抽水蓄库的“调峰”水库,部分水库弃水又是下游水库的水源之一.河网弃水是江道水库的来水之一,而沿曹娥江和姚江两岸的翻水站又抽取江道水库蓄水向片区供水.
(7)供排水方向不一致 平原河网区以河网引水为主,水资源配置方向是由西向东,排涝方向则由南向北排入钱塘江.
(8)有调节供水与无调节供水相结合 除调节性能较好的山区水库外,平原河网和江道水库汇水仅靠河道高水位与低水位之间的蓄水容积调节,调蓄性能较差.
综上所述,研究对象是一个以河网引水为主的跨行政区、跨流域、多水源、多用户、多层次、多级串并联、多级反馈的大型水资源配置系统.
2.2 浙东水资源系统概化
浙东水资源系统中的各区域通过各种水利工程相联通,从而实现引入的钱塘江水资源与浙东地区水资源的统一配置.钱塘江水源通过浙东引水萧山枢纽工程在浙东地区有引水需求的情况下有条件有限制地(时间和水量)向浙东水资源系统供水.位于曹娥江闸上水库上游的山区径流全部汇入水库,而曹娥江闸上水库还将左岸的萧绍平原和右岸的姚江平原两个不同水系、不同水级的平原河网联系起来,通过三兴引水闸和大厍引水闸将钱塘江和曹娥江水资源引至曹娥江右岸的姚江流域,使曹娥江河口两岸成为一个共同的供水体系.舟山大陆引水工程则将舟山片与姚江平原南片联在一起,通过海底输水管道向舟山提供水资源.浙东引水水资源系统概化网络图见图1.
3 浙东水资源系统仿真模拟数学模型
模拟是对水资源系统及其功能的直接模拟,也是分析复杂水资源系统的重要手段[1-2].为了真实模拟浙东引水工程的运行状况,本次建立浙东水资源系统仿真模拟模型,主要由产汇流模拟模型、水量配置模拟模型和河网水动力模拟模型组成.
3.1 产汇流模拟模型
产汇流模拟模型依据各类下垫面的降雨径流特点,采用相应的方法计算其径流过程,同时模拟农田灌溉需水过程,为水量配置模拟模型提供边界条件.
山区径流模拟一般采用年径流模型法、水文比拟法及降雨径流相关法;平原径流模拟则按不同的下垫面条件(水面、水田、旱地、杂地)分别采用不同的产流方式计算.

图1 浙东引水工程水资源系统概化网络图
3.2 水量配置模拟模型
水量配置模拟模型以水资源分区为基础,将研究区域划分为多个计算单元,模型根据水量平衡原理,依照一定的计算顺序和准则模拟各计算单元内的取用水过程和计算单元之间的水量交换过程,并为河网水动力模拟模型提供边界条件[3-5].
3.2.1 目标函数
系统缺水总量最小:
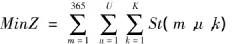
其中:St(m,u,k)—第u个计算分区第k用水户第m时段的缺水量.
3.2.2 约束条件
(1)水量平衡约束
计算分区水量平衡约束:
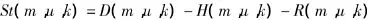
其中:D(m,u,k)—第u计算分区第k个用水户第m时段的需水量;
H(m,u,k)—第u计算分区第k个用水户第m时段的河网供水;
R(m,u,k)—第u计算分区第k个用水户第m时段的水库供水.
水库(河网)水量平衡约束:

其中:V(m,i)—第i个水库(河网)第m时段初始蓄水量;
V(m+1,i)—第i个水库(河网)第m时段末蓄水量;
Vs(m,i)—第 i个水库(河网)第m时段水库(河网)的来水量;
Vg(m,i)—第i个水库(河网)第m时段水库(河网)的供水量;
Vw(m,i)—第i个水库(河网)第m时段水库(河网)的弃水量;
L(m,i)—第 i个水库(河网)第m时段水库(河网)损失量.
(2)蓄水库容约束
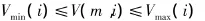
其中:Vmin(i)—第i个水库(河网)的供水死库容;
V(m,i)—第i个水库(河网)第m时段的蓄水量;
Vmax(i)—第i个水库(河网)的控制蓄水量,梅汛期、台汛期和非汛期采取不同的控制.
(3)引提水量约束

其中:P(y,m,u)—第u计算分区第m时段引、提水量;
Pmax(u)—第u计算分区的最大引提水能力.
(4)最小供水保证率约束:
优质水供水保证率95%以上,一般工业、农灌供水保证率85%~90%.
3.3 河网水动力模拟模型
河网水动力模拟模型基于各骨干输水河道和控制性水利工程,由反映质量守恒定律的连续方程和反映动量守恒定律的运动方程组成,将平原地区的汇水和用水排水过程分别作为骨干河道的正向或负向集中入流概化在模型中,依照区域总体水流方向和控制性水利工程启闭原则,逐时模拟河网中骨干引水河道的水流运动,依次计算各断面的水位、流量.河网水动力模拟模型的框架结构如下:
(1)描述河道直河段水流运动采用一维的圣维南偏微分方程组:
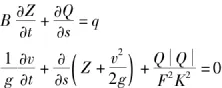
其中:Z、Q、F、v、K—分别表示某一时刻 t及在某空间位置S断面处的水位、流量、相应过水断面面积、断面平均流速和流量模数;
q—单位河长旁侧入流量.
(2)描述河道汊点,采用有调蓄连接的零维模型,即遵循水量平衡原理,即流入汊点的净水量等于区域内的蓄量增量:

(3)描述闸汊,由于河道上水闸的过闸水流一般属于堰流(宽顶堰或实用堰),过闸水流之水位可不连续,但过闸流量连续,忽略水闸附近的水量调节,则:
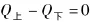

其中:Z上、Z下—闸上、下游水位;σ—淹没系数;
ε—侧收缩系数;m—流量系数;
B—溢流宽度;H0—有效水头.
Sign(x)为符号函数,当 x<0、=0、>0,函数值分别是 -1、0、+1.
4 曹娥江至宁波引水工程曹娥江最低可引水水位方案比选
浙东引水萧山枢纽和曹娥江至宁波引水工程是整个浙东引水水资源系统的重要节点工程.目前,《钱塘江河口水资源配置调度办法(试行)》已经颁布实施,萧山枢纽将遵循《调度办法》中的原则进行引水调度,因此,确定曹娥江至宁波引水工程曹娥江最低可引水水位成为影响浙东引水工程配置效果的关键所在.该水位如果定得过高,会影响曹娥江至宁波地区的引水量;定得过低,又会影响萧绍平原河网的蓄水.因此,本次需要通过水量配置模拟模型和河网水动力模拟模型对曹娥江至宁波引水工程曹娥江最低可引水水位进行方案比选.
4.1 水量配置模拟方案比选
曹娥江闸上水库的正常蓄水位为3.9 m,低水位为3.3 m,根据闸上水库特征水位,本次拟定了5个最低可引水水位方案,即 3.9 m、3.75 m、3.6 m、3.45 m和3.3 m.各方案计算成果见表1和表2.

表1 曹娥江最低可引水水位方案比选成果

表2 曹娥江最低可引水水位方案比选成果
从表中可以看出:
(1)萧山枢纽引水量.曹娥江最低可引水水位由3.9 m降至3.3 m时,萧山枢纽多年平均引水量逐渐增加,但差别不大,多年平均引水量8.8~8.9亿m3,基本达到萧山枢纽设计多年平均引水量.
(2)曹娥江以西地区供水保证情况.曹娥江最低可引水水位由3.9 m降至3.3 m时,曹娥江以西的萧山蜀山平原有富春江引水作保证,供水未受影响;绍虞平原抗旱水量主要由河网及曹娥江闸上水库提供,曹娥江最低可引水水位越低,绍虞平原干旱年份的缺水量随之略有增加,但事实上,由于富春江引水,绍虞平原供水保证率和干旱年份缺水程度较现状工况均有明显好转.
(3)曹娥江以东地区供水保证情况.曹娥江最低可引水水位由3.9 m降至3.3 m时,曹娥江以东地区从曹娥江闸上水库多年平均引水量增加,以90%保证率的1978年为例,当最低可引水水位为3.9 m时,曹娥江以东地区的引水量为6.08亿m3,达不到设计要求,此时姚中片和宁西片仍有缺水;当最低可引水水位为3.75 m时,曹娥江以东地区的引水量为7.10亿m3,达不到设计要求,此时姚中片和宁西片略有缺水;当最低可引水水位为3.6 m时,曹娥江以东地区的引水量为7.49亿m3,略微超过设计要求,此时曹娥江以东各片区供水满足要求;当最低可引水水位为3.45 m和3.3 m时,曹娥江以东地区的引水量分别为 7.74亿 m3和7.93亿m3,均超过设计要求,此时曹娥江以东各片区供水也满足要求.
综上所述,当曹娥江最低可引水水位为3.6 m时,萧山枢纽引水和曹娥江以东地区引水均能达到设计要求,该水位对绍虞平原的影响不大,且此时曹娥江以东地区供水满足要求.因此,推荐曹娥江至宁波引水工程曹娥江最低可引水水位为3.6 m.
4.2 河网水动力模拟方案比选
按照水量配置模拟中拟定的5个曹娥江至宁波引水工程曹娥江最低可引水水位方案,即3.9 m、3.75 m、3.6 m、3.45 m 和3.3 m 分别进行河网水量动力模拟.各方案计算成果见表3.

表3 河网特征水位多年平均历时统计
从表中可以看出:随着曹娥江最低可引水水位的降低,绍虞平原河网低于特征水位3.0 m、3.3 m和3.6 m的多年平均时间逐渐增加,尤其是当曹娥江最低可引水水位为3.3 m时,绍虞平原河网低于中水位3.6 m的时间明显高于其它方案;对于宁波地区的下姚江来说,随着曹娥江最低可引水水位的降低,下姚江江道高于特征水位-3.07(吴淞-1.2 m)、0.73(吴淞2.6 m)、0.93 m(吴淞 2.8 m)的时间逐渐增加,但增幅较小.结合水量配置模拟模型的方案比选成果,从尽量减少对绍虞平原河网水位的影响出发,推荐曹娥江最低可引水水位3.6 m是合适的.
5 结语
浙东水资源系统仿真模拟模型首次全方位地模拟了大型引水工程水资源系统中水资源的产生、输送、取用和回归的全过程,利用该模型系统进行长系列逐日水资源配置调度方案分析,可以为浙东引水工程建成后的良性运行提供技术支撑.该模型系统可以为类似工程的水资源配置、调度运行方案比较等提供参考.
[1]叶秉如.水资源系统优化规划和调度[M].北京:中国水利水电出版社,2001.
[2]游进军.水资源系统模拟理论与实践[D].北京:中国水利水电科学研究院,2005.
[3]黄 昉,许文斌,郑建青.多水源多用户大型水资源系统优化模型[J].水利学报,2002,33(3):91-96.
[4]甘治国,蒋云钟,鲁 帆,等.北京市水资源配置模拟模型研究[J].水利学报,2008,39(1):91-95.
[5]谷媛媛,矫振宽,朱红玉,等.区域多水源联合调配供水研究[J].河北工程大学学报:自然科学版,2008,25(4):69-72.

