等价鞅测度模型在欧式认股权证定价中的应用
张凯凡
(湖北工业大学 理学院,武汉 430068)
认股权证是国际证券市场上流行的一种初级的股票衍生产品.认股权证是授予持有人一项权利,在到期日前(也可能有其它附加条款)以行使价购买公司发行的新股(或者是库藏的股票).认股权证往往被视为现货市场产品,因为其买卖方式类似股票,而非期权和期货等衍生产品.不过认股权证同时具备衍生产品的许多特点,可以作为一种非常好的杠杆投资工具等.但是有关认股权证的研究较少,并且多集中在认股权证的市场价格的统计分析描述.本文从Black-Scholes[1]模型出发利用等价鞅测度定理得到了欧式认股权证定价的一般公式.
1 模型与定义
1.1 理想模型
1)金融市场为有效的稳定市场,分为无风险资产和风险资产两种,前者一般称为债券,后者称为股票,它们分别满足下式

其中,St表示股票在t时刻的价格,Bt表示债券,μ表示股票的期望收益率,r为无风险利率,σ表示波动率,μ、σ、r均为常数,dWPt表示布朗运动在概率测度P下的t时刻的瞬间增量.
2)股票在期权持有期内无红利支付.
3)股票交易连续进行,不存在交易费用及交易税.
1.2 定义
设(Ω,F,P)是一概率空间,Fn是F 的完备子σ-代数的一个增加族,满足F=∨nFn,其中F0={φ,Ω},P是风险概率测度,(WPt,0≤t≤T)是概率空间上的一维标准布朗运动,Ft是由WPt生成的σ-代数.
定义如果测度Q满足


定理1 在测度Q下,股票价格的动态过程为
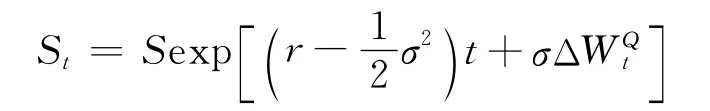
证明 股票的价格过程满足(1)式,应用ltô定理,有

进而求得在测度P下,股票价格的动态过程为

其中E(·)为在测度P下的数学期望,PQ(·)为在测度Q下的概率,IA为A的示性函数,将式(5)代入式(3),得到

所以在测度Q下,有


2 主要结果
考虑一般性的定价问题:设某上市公司拥有x股已发行的流通股票,有y份流通的认股权证,且认股权证的持有者在时刻T可以以每股X的执行价格从该公司购买z股的股票,用W 表示每份认股权证现在时刻(T=0)的价值,用V表示该公司现在时刻的权益价值.
定理3 在上述条件下,认股权证现在(T=0时刻)的价格为


证明 设T时刻认股权证被执行,此时执行价格为yzX,因此公司权益价值为VT+yzX.股票总股数变为x+yz,那么T时刻的瞬间股票价格为

这时,认股权证持有者就会获得收入为

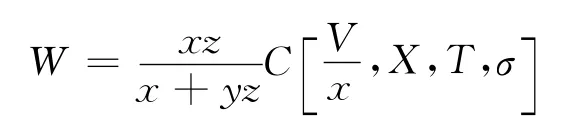
其中,σ表示公司权益价值的波动率.

且有

用P表示风险中性概率测度,则有
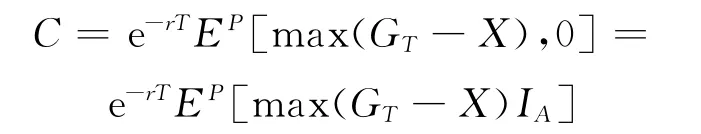
于是

显然

在测度P下,标的资产G的随机动态过程为


通过类似的方法,可以得到
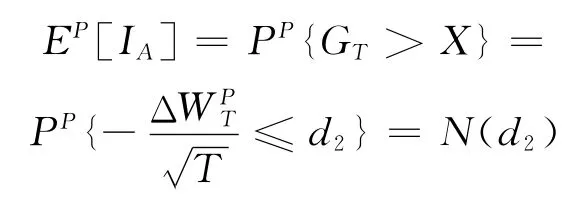
其中

因此,定价公式(8)化为
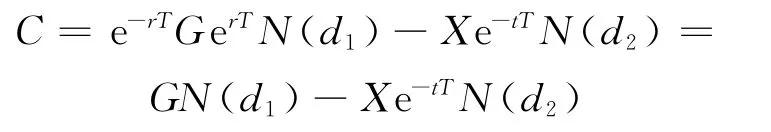
从而认股权证的定价公式为

3 结 语
对股权证价格W 的定价公式(7)中的波动率的计算,可以通过计算变化的波动率,这里X是认股权证的市场价格.基于股票价格和认股权证价格的历史数据,可以采用时间序列模型中的历史波动率的计算方法.在以上基本公式中,对其基本假设进行修正,可以得到一些应用于特殊情况的权证定价公式,如附保底条款的鞅定价模型、公司发放红利的定价模型以及随机利率下认股权证的定价模型等.和股票期权(Zhu Yonggang.Applications of Martingale Methods in Stock Index Option.Recent Advance in Statistic Application and Related Areas,2010-07.)一样,认股权证是一种以小博大的金融工具,对投资者很有吸引力,按照资本市场的理论,收益越大,风险也越大.如何控制认股权证的价格风险,还有待于继续研究.
[1]Black F,Scholes M.The Pricing of Options Corporate Liabilities[J].Journal of Political Economy,1973,81(3):637-659.
[2]孔繁亮.B值渐近鞅的强弱大数定律[J].数学学报,1998,41(3):667-672.
[3]Martin B.Finacial Calculus[M].England:Cambridge University Press,1997.
