基于客户等级的可承诺量预分配策略研究

王 涛，陈淮莉

(上海海事大学科学研究院，上海 200135)

可承诺量(available to promise，ATP)是指在同时考虑产能、物料和客户需求等各种企业资源约束的前提下，由企业主计划产出的用于进行未来订单配置的产品库存量与计划生产量中尚未分配到客户订单的那部分产品量。

在当今这个竞争不断加剧的市场，客户的需求千变万化，能否对客户订单做出及时、可靠的承诺已经成为决定企业胜负的关键问题之一。因此，以可承诺量预分配为基础的订单配置研究逐渐被重视。将供应链系统主计划(MP)产出的所有ATP分配到客户区域的过程即供应链ATP预分配，其内容是先对订单按某种规则进行排序，然后将主计划产出的可承诺量结果分配给完成排序后的订单。订单配置是在ATP分配的基础上对实际到达的客户订单需求进行交货数量和时间的承诺[1]，当分配的ATP不足时，首先考虑满足(或部分满足)那些订单能使其利润最大化的客户。由此带来ATP分配计划中分配规则，订单配置中ATP冲减的综合应用问题。

1 可承诺量预分配

1.1 问题的提出与假设

早些年对ATP预分配的研究主要集中在多约束条件下的计算问题，如CHEN等用混合整数规划法计算了批量处理方式下的ATP交货数量和时间，在ATP计算时考虑了供应链材料、能力约束以及客户化产品配置等问题[2];接着，CHEN等对其2001年提出的模型进行优化，将客户的优先级考虑进去，同时就订单处理批量对该模型性能的影响进行了详细的分析[3]。基于CHEN的研究，又将可承诺量细分为成品ATP、能力ATP、系列产品ATP、零件和原材料ATP、渠道ATP和配送ATP等，对此也有学者进行了细致的研究，如JEONG等通过主生产计划计算车间生产能力ATP，建立全球供应链ATP模型推算新订单的产品发送时间[4]。JUNG等提出了一个基于供应链环境的可承诺量系统，对整个供应链的运输配送能力、生产能力和库存控制进行了考虑[5]。

近些年对ATP分配的研究更加注重多维度、动态性，如DULLURI等提出了一个适应于单生产厂多客户环境的ATP分配模型，在该模型中不仅考虑了多种具有随机需求的产品和变化的利率，同时还考虑了生产学习曲线和动态价格策略[6]。TSAI等提出基于订单装配制造环境的多生产工厂的可承诺量计算模型，并将其应用于当地的一家液晶显示器制造企业[7]。HERBERT对ATP粒度的客户维、产品维和时间维进行了不同维度的划分组合，同时建立了ATP分配及消费模型，并应用仿真技术得出不同维度组合下企业的利润[8]。

综上所述，目前对ATP预分配的研究虽然已取得一定的成果，但缺乏实用性，大多基于需求已知的基础来对ATP预分配进行研究，并且分配方法中鲜有考虑客户优先级。针对该问题，笔者在随机需求的基础上考虑客户的优先级，利用以下模型对ATP进行预分配。

模型假设:工厂生产模式为MTS，故只需要考虑其产成品，而不需要考虑中间产品;只生产一种商品，顾客级别分为两级，且只允许消耗各自的ATP;在整个计划期内货物补充的时间和次数是固定的;订单一经承诺就不能更改。

假设企业只生产一种产品，并且将整个计划期分为若干个小时间段，每个时间段中工厂面对随机到来的两个客户等级的订单进行订单的接受和配给，而整个计划期内的货物补充是已知且固定的。那么第t个时间段ATP的量就取决于已经履约的订单及现有的库存量，计算公式为:

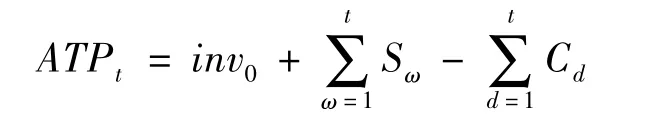
其中:inv0为期初库存;S为每期的库存补充量;Cd是到期日为d的已经承诺的订单量。

1.2 预分配模型的建立

1.2.1 无货物补充情况

假设在整个计划期内无库存补充，期初Cd=0，则初始库存等于整个计划期的ATP的总量。ATPH为分配给高优先级客户的量，记QH为整个计划期内高优先级客户的需求量，其对应的分布函数为F(·)。给定企业要达到的高级客户的服务水平∂，则可通过下面的约束求出ATPH:

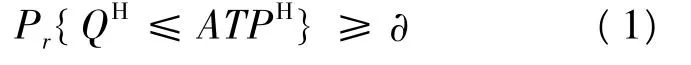
根据QH的分布函数，可以将式(1)转化为:

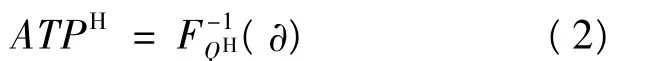
与此同时，ATPH还受到初始库存量的约束，综合式(1)和式(2)，可表达为:

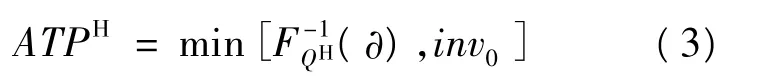
1.2.2 有1次货物补充情况

假设货物补充发生在时刻t*，补充量为S，将整个计划期分为两个时间段:第一个时间段为t=1，2，…，t*－1，第二个时间段为 t=t*，t*+1，…，T。QH1，QH2分别为第一、第二个时间段内高优先级客户的需求量;ATPH1，ATPH2分别为第一、第二个时间段内高优先级客户的预分配量。为使高优先级客户在第一时间段内达到服务水平∂，有:

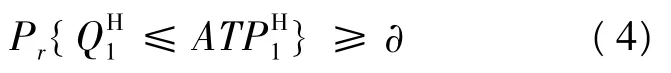
但在计算ATPH2时必须要考虑在库存补充时间点t*(第一时间段期末)高优先级客户ATP是否有剩余。如有剩余量，即(ATPH1－QH1)+将继续用在下一时间段中，表示为:

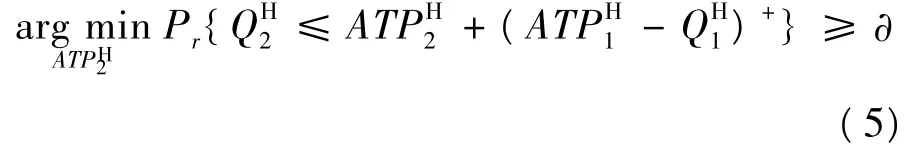
其中，ATPH1的值可以通过式(4)求出，代入式(5)可得ATPH2的表达式为:

式(6)中QH2－(ATPH1－QH1)+的量，可以通过大量数据仿真，再运用二阶矩估计来近似求出。

与此同时为了减少库存成本和不影响低优先级客户的订单履约，将货物补充量S的部分或全部作为ATPH2。因此ATPH2在满足式(6)条件下，还将受到库存补充S的约束，如果ATPH2＞S，其短缺量必须在第一时间段提前预留。例如经过计算，第二时间段内高优先级客户为达到服务水平∂，需要200单位货品，而货物补充只有180单位，则不足的20单位就需要在第一时间段内提前预留，并且不允许在第一时间段内消耗掉。表达为:

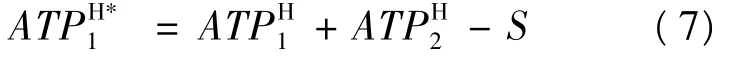
根据以上分析可将整个计算过程表示如下:

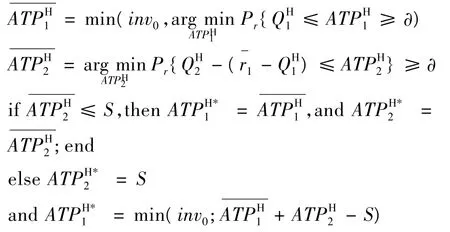
1.2.3 货物补充的次数大于1

假设有n次货物补充，则将整个计划期分为n+1 段:[1，t1－1]，[t1，t2－ 1]，…，[tn，T]，而ATPHi、QHi、Si分别为第i段所对应的高优先级客户预留量、需求量以及货物补充量，从第一时间段进行计算得到:

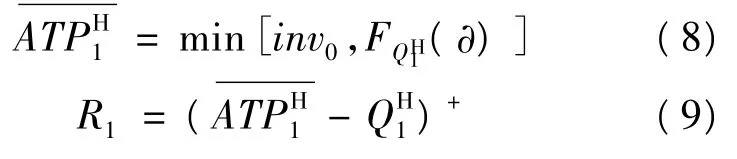
R1为第一时间段期末高优先级客户剩余的ATP，它将继续预留在第二个时间段内:

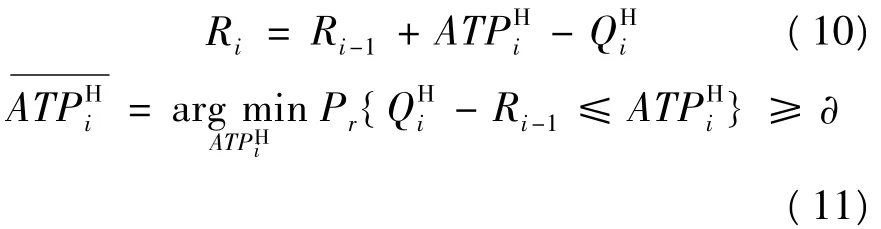
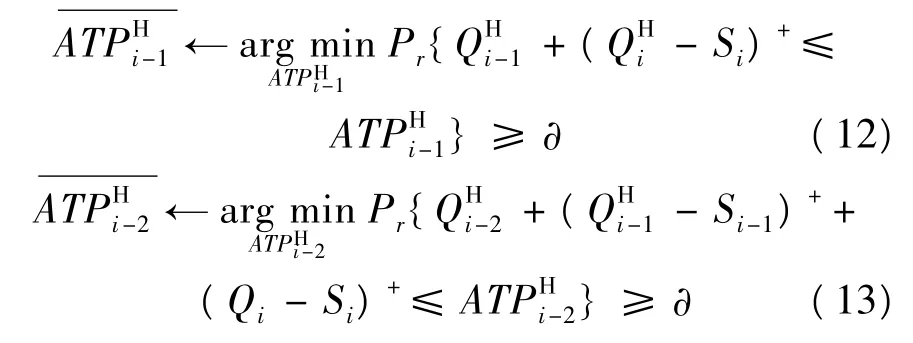
综上可将整个过程表示为:

1.3 收益分析

整个计划期内有n次货物补充，现对其进行收入分析。根据上述分析，将整个计划期分为n+1段，定义变量如下:P为产品价格;C1为产品成本;C2为产品单位时间的库存成本;Ti为第i时间段产品的库存时间;fH(x)为高优先级客户的需求概率密度函数;fL(x)为低优先级客户的需求概率密度函数;ATPHi为第i时间段内高优先级客户ATP的预分配量;EHi为第i时间段内高优先级客户的期望收益;ELi为第i时间段内低优先级客户的期望收益;E库存为计划期内总库存成本的期望值;E总为计划期的总体收益的期望值。

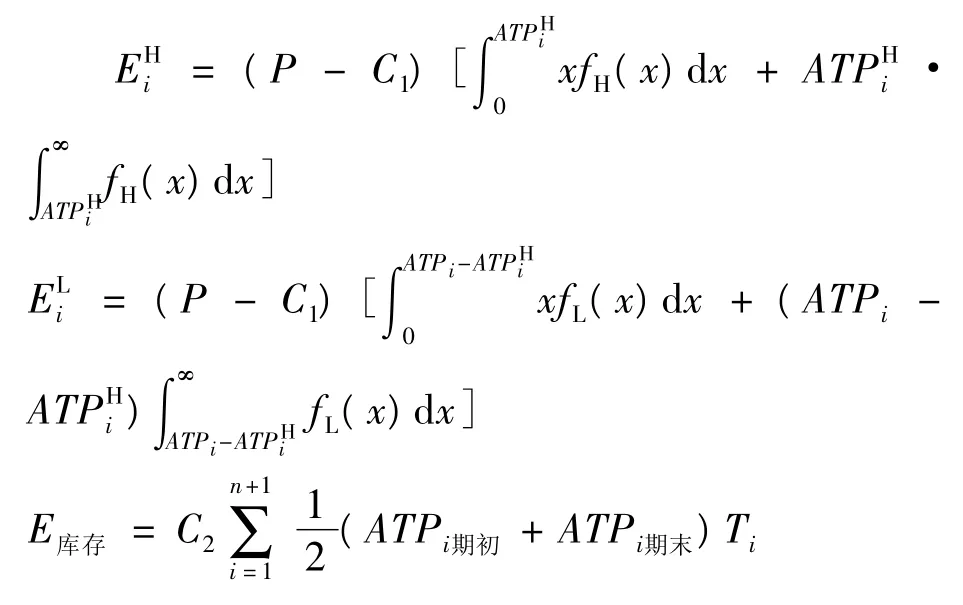
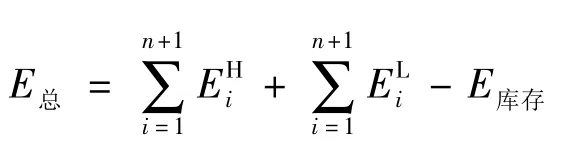
2 算例

2.1 ATP预留量分析

在不同需求特征下对ATP按照客户等级进行预分配，并对先进先出策略下(对所有客户一视同仁)订单的总体收益和履约率进行比较分析。

假设整个计划期为15天，共有4次货物补充，每次的补充量为220，期初ATP的量为2 200。那么将整个计划期分为5个时间段，每个时间段低优先级客户的需求量为QL～N(400，202)，高优先级客户分别取QH～N(200，502);QH～N(200，202)两种不同的方差来进行讨论。高优先级客户要达到服务水平(0.50、0.60、0.70、0.75、0.80、0.85、0.90、0.95)，则在不同方差情况下的每个时间段其ATP应达到的量如表1和表2所示。

表1 QH～N(200，502)时各服务水平对应的ATP

表2 QH～N(200，202)时各服务水平对应的ATP

表1为每期高优先级应该持有的ATP量，但是在期初预留ATP时要考虑到货物补充量以及每个时间段末ATP剩余量的影响，因此应根据模型，通过迭代算出每个时间段ATP的预留量。下面选取服务水平为0.70，0.85，0.95计算各服务水平应预留的ATP，如图1所示。

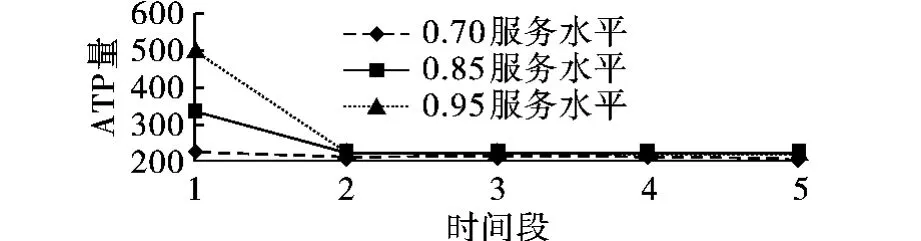
图1 QH～N(200，502)各服务水平应预留的ATP

从图1可以看出，当服务水平为0.70时，各时间段需要为高优先级客户预留的ATP量变化不大。除第一时间段以外，各时间段的ATP预留量均小于或等于补充量220，因此在期初只考虑第一时间段所需的ATP量即可。第一时间段ATP的预留量只比后几期略高，这是因为考虑到第一时间段末ATP的剩余量会自动滚入下一时间段。当服务水平为0.85和0.95时，各时间段高优先级客户对ATP的所需量大于货物补充量，即需要在期初提前预留。可以看到此时随着服务水平的提高，期初需要预留的ATP量有显著上升。

从图2中可以看出当服务水平为0.70和0.85时，第一时间段后，每段内需要预留的ATP量均小于货物补充量，虽然各个时间段有波动，这是由于仿真中的数据生成的随机性所造成的。当服务水平为0.95时，预留量大于货物补充量，需要在期初提前预留。

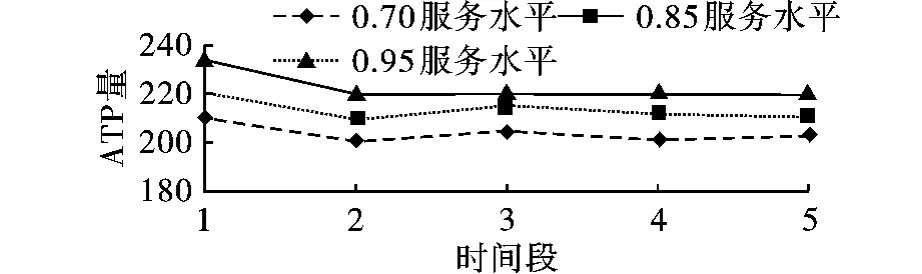
图2 QH～N(200，202)各服务水平应预留的ATP

比较图1和图2可以得出，当预测较准确及需求函数方差较小时，只需要在期初预留较小的ATP量，就可以为高优先级客户保证较高的服务水平。

2.2 收益分析

假设每单位产品出售给高优先级客户可以获利15元，而给低优先级客户则为10元，每单位库存成本为2元/5 d。通过收益分析计算可得不同方差下的动态分配策略对总体收益的影响如图3和图4所示。总体收益如表3和表4所示。

图3 QH～N(200，502)动态分配策略对总体收益的影响

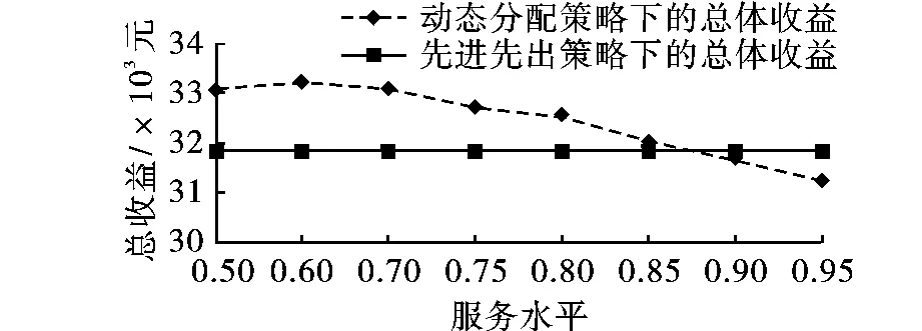
图4 QH～N(200，202)动态分配策略对总体收益的影响

表3 QH～N(200，502)动态分配策略对应的总体收益

表4 QH～N(200，202)动态分配策略对应的总体收益

由图3可知，从0.50开始，随着服务水平的提高，总体收益也在不断地增加，一直到服务水平为0.80时达到最高点。在较低的服务水平下，大量的ATP被低优先级客户消耗，从而导致高优先级客户的订单得不到满足。随着给高优先级客户预留ATP量的增加，较多高优先级客户的订单被优先满足，给企业带来较多的收益。然而当服务水平设置在0.80以上时，收益有了明显的下滑，当服务水平在0.90之后，下降到先进先出策略下的总体收益。这是由于给高优先级客户预留的ATP过多，使得在期末有了大量剩余，这使得原本可以接受的低优先级客户的订单被拒绝，也产生了较高的库存成本。

由图4可以看出服务水平在0.60时，总体收益较大，当服务水平增高时，总体收益降低。此时需求函数的方差较小，即预测较为准确，高优先级客户的需求量落在200左右的概率比较大。当服务水平设置较高时，高优先级客户充分利用预留的ATP成为小概率事件。此时会造成部分预留量剩余，从而影响低优先级客户的履约，并产生较高的库存成本。

2.3 订单履约率分析

不同服务水平的设置对订单总体履约率也有一定的影响。根据上述所假设的需求特征，对不同服务水平下各个时期高低优先级客户的订单进行仿真，得到不同方差下的履约率，如图5和图6所示。

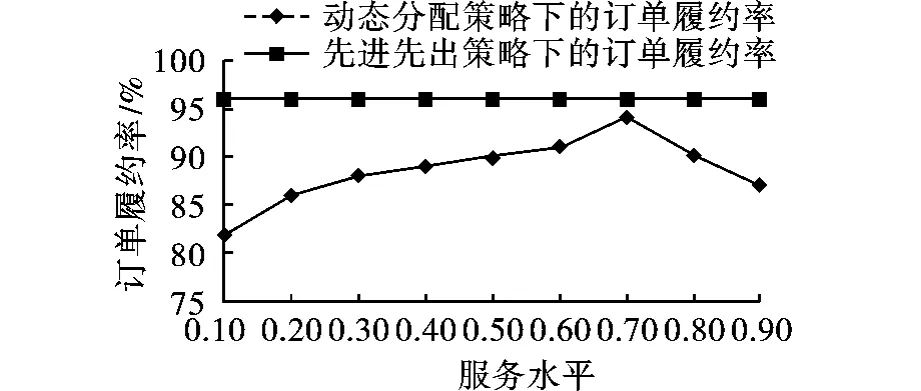
图5 QH～N(200，502)动态分配策略对订单履约率的影响

从图5可看出，当采用先进先出策略时，订单的总体履约率最高，但是此时无法保证高优先级客户的利益，因此，此时的总体收益是较低的。在订单配置前将ATP按照客户服务水平预留部分给高优先级客户，可以保证较高的总体收益，但总体履约率相对偏低。当服务水平较低时，由于把高低优先级客户的ATP区分开来，导致大量的高优先级客户订单无法满足。随着服务水平的增高，履约率不断增高，直到服务水平达到0.70时，履约率达到最高值。当服务水平高于0.70时，高优先级客户的ATP较多，会有部分剩余，而部分低优先级客户订单却会被拒绝，造成总体履约率的下降。

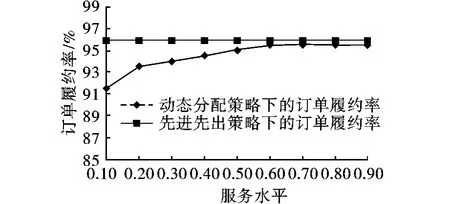
图6 QH～N(200，202)动态分配策略对订单履约率的影响

从图6可看出，随着服务水平的增高，履约率有较小的增幅，但当服务水平在0.60之上，履约率趋于稳定。从表2的结果来看，各服务水平下所对应的ATP预留量相差不大，且高优先级客户的需求量落在200附近的概率较大，因此，总体来说服务水平的设置对履约率影响不是很大。

由以上分析可以得出:与先进先出策略相比，预分配的方式下总体收益会有较明显的提高，而订单履约率会有所下降，需要决策者对服务水平设置的范围进行合适的选择。在企业的需求函数满足 QH～N(200，502)，QL～N(400，202)时，决策者按照实际情况将高优先级客户的服务水平控制在(0.65，0.85)之间较为合适;需求函数满足QH～N(200，202)，QL～N(400，202)时，高优先级客户的需求落在200附近的概率较大，如预留较多的ATP会使低优先级客户无法充分履约，考虑到总体收益，选择(0.60，0.70)范围内较为合适。此时总体收益较高，且订单总体履约率相对先进先出策略只有较小幅度下降，因此选择该范围的服务水平，无论是对企业的短期盈利还是长期收益都较为有利。

3 结论

在订单的配置过程中，ATP预分配的合理性，不但直接影响订单的履约率及收益，而且对企业的响应时间及竞争能力等都将产生重要的影响。由此可见，科学合理地对ATP进行预分配，对企业具有重要的现实意义。笔者主要讨论了在MTS生产环境下可承诺量在客户等级维度上的预分配。在假设需求不确定的情况下，通过引入客户服务水平这一概念，提出了一种动态的在客户等级层次上对ATP配置的策略。在此基础上进行收益分析和订单履约率分析，给企业决策提供了一个更广阔的视角。

[1] HARTMUT S，CHRIDTOPH K.Supply chain management and advanced planning － concepts，models，software and case studies[M].Germany:Springer Berlin Heidelberg，2005:22－192.

[2] CHEN C Y，ZHAO Z Y，MICHAEL O B.Quantity and due date quoting available to promise[J].Information Systems Frontiers，2001(4):477 －488.

[3] CHEN C Y，ZHAO Z Y，MICHAEL O B.A model for batch advanced available－to－promise[J].Production and Operations Management，2002(11):424 －440.

[4] JEONG B，SIM S B，JEONG H S.An available－ to －promise system for TFT LCD manufacturing in supply chain[J].Computers ＆ Industry Engineering，2002(43):191－212.

[5] JUNG H，SONG I，JEONG B J，et al.An optimized ATP system for make－to－order company in supply chain environment[J].Industrial Engineering:Theory Applications and Practice，2003(10):367 －374.

[6] DULLURI S，RAGHAVAN N，SRINIVASA R.Revenue management via mult－product available to promise[J].Journal of Industrial and Management Optimization，2007(3):457 －479.

[7] TSAI K M，WANG S C.Multi－site available－topromise modeling for assemble－to－order manufacturing:an illustrantion on TFT － LCD manufacturing[J].Int J Production Economics，2009(117):174 －184.

[8] HERBERT M.Customer segmentation，allocation planning and order promising in make－to－stock production[J].OR Spectrum，2009(31):229 － 256.