改进蜜蜂群算法的最优种群结构研究
徐卫滨
(太原科技大学经济与管理学院,太原030024)
在现实世界中,许多系统都可以用复杂网络来描述,如生物网络中的代谢网[1]、蛋白质网[2]等。这些真实的网络,在变化的环境中通过不断地改变结构来保持他们的性能。
为了理解真实的网络,学者们设计了各种各样的、能够反映真实网络特征的网络模型,如,ER随机网络模型[3]、WS小世界模型[4]和 BA 无标度网络模型[5]。这些反应真实系统特征的网络模型将有助于群智能算法问题中最优种群结构的设计[6]。SANTHOJI[7]提出设计群智能算法最优种群结构的方法论,其是以种群结构具有较强的信息转移能力、最少的边(资源)和算法具有最优的性能为目标。同时,SANTHOJI以PSO算法为例,基于ER随机网模型和NW小世界模型的演化机制研究了PSO问题最优种群结构。借鉴SANTHOJ设计PSO最优结构的方法论,基于ER随机网络模型演化机制,研究一种改进蜂群算法(MABC)的最优种群结构,即以最小的资源(边),最大信息转移能力(结构熵)和最优的MABC性能为目标,设计最优种群结构。
1 网络的特征度量
在对复杂网络研究的过程中,学者们提出了一些概念和度量方法以表示网络的结构特征。
(1)度(k):节点i的度ki定义为与该节点连接的其他节点的数目。
(2)度分布(P(k)):网络度的分布情况用分布函数P(k)来描述。P(k)表示的是一个随机选定的节点的度恰好为k的概率。pki表示微粒i具有度k的概率。
(3)平均度(<k>):网络中所有节点i的度ki的平均值。
(4)结构熵(E):熵表示系统存储,处理和转移信息的能力。在复杂网络中,熵可以表示网络结构的异质程度及网络结构转移信息的能力。在复杂网络里定义节点i的熵为:Ei=-pkilog2pki,则整个网络的熵为:
2 ER随机网络模型
Erdös和Rényi(ER)最早提出随机网络模型并进行了深入研究,他们是用概率统计方法研究随机图统计特性的创始人。ER模型是基于一种“自然”的构造方法:假设有n个节点,并假设每对节点之间相连的可能性都是常数0<p<1,这样构造出的网络就是ER模型网络。

图1 不同概率p值的ER网络模型Fig.1 ER network with different probability p
科学家们最初使用这种模型来解释现实生活中的网络。ER随机网络有一个重要特性,就是虽然节点之间的连接是随机形成的,但最后产生的网络的度分布是高度平等的,即大部分的节点的度都集中在某个特殊值附近,成钟形的泊松分布规律。
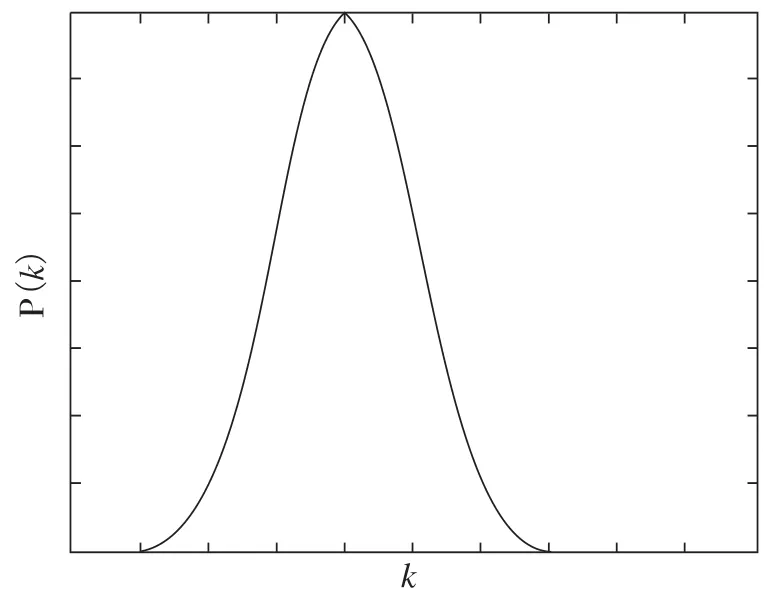
图2 ER网络模型的度分布图Fig.2 The degree distribution of ER netwrok
图2中,横坐标k代表网络的度,纵坐标P(k)代表随机取一节点度为k的概率。
3 改进的蜜蜂群算法(MABC)
根据蜜蜂的交配行为和觅食行为,学者设计了蜜蜂群优化算法[8-9]。其中文献[9]根据蜜蜂的觅食行为设计出用于解决连续函数优化问题蜂群算法(ABC)。ABC算法由三种蜂组成:引领蜂、跟随蜂和侦察蜂。由于ABC算法采用比例的适应值选择策略,则易降低算法的种群多样性和全局优化性能,进而导致算法停止进化。针对这一问题,文献[10]对其进行改进,不设置跟随蜂,以使算法获得更好的收敛效果。在MABC算法中,引领蜂按照式(1)进行食物源开采:

其中,i表示第i个解(食物源),k∈{1,2,…,N}(N表示种群规模)表示随机选取的不同于i的解,j表示解的第j维向量(其是随机选取的)。Φij是[-1,1]上的一个随机数。
当MABC算法搜索到的最好解在连续的limit次迭代内未得到改善时,这个解(食物源)被放弃。同时,由侦察蜂通过式(2)随机搜索产生一个新解作为解。

其中,i表示第i个解,xmin和xmax分别表示域的下限和上限。
3.1 改进蜜蜂群算法步骤
Step 1 初始化,随机产生N个解(引领蜂)作为食物源,并计算每个解的适应值;
Step 2 依据式(1),N个引领蜂进行搜索产生新的N个解vi(i=1,…,N),并计算其适应值;
Step 3vi与xi的适应值进行比较,若vi的适应值优于xi,则用vi替换xi,将vi作为当前最好解,否则保留xi;
Step 4 通过limit值判断是否存在需要放弃的解,若存在,则依据式(2)产生新解,替代被放弃的解;
Step 5 比较N个解,保留最优的作为全局最好解;
Step 6 迭代次数加1;
Step 7 判断是否满足终止条件,若满足则输出最优结果,否则返回Step 2.
4 MABC的最优种群结构
在复杂网络中,熵可以表示网络结构的异质程度及网络结构信息转移能力。当结构的熵值较小时,结构转移信息的能力较弱;当结构的熵值较大时,结构转移信息的能力较强。结构中边的数量(可以用结构的平均度值来表示)可以表示求解函数优化问题时所需花费的成本代价。当结构边的数量较少时,解决优化问题所需的代价较小;而当结构边的数量较大时,解决优化问题所需的代价较大。算法性能表示了整个系统的功能。如果算法性能优,则系统功能强,反之则不然。因此,评价算法最优种群结构的标准是:结构熵、结构的平均度(边的数量)和算法的性能。获得算法的最优种群结构需要最大化结构熵、最小化结构的平均度和最优的算法性能。
基于ER随机网络模型的演化机制,以50维的Rosenbrock(收敛精度为1)函数为例,对MABC算法的最优种群结构进行研究。
研究方法:对于有N个微粒的种群而言,共进行次实验。第一次实验种群结构边的数量n=0条,第二次实验种群结构边的数量n=1条,第三次实验种群结构边的数量n=2条,依次类推,第次实验种群结构边的数量为条,即完全连接的结构。
第i次实验执行两步:
(1)按照ER网络模型演化机制以概率P=随机连接每对节点,计算结构的平均度和熵值,并将熵值归一化,即H/Hmax;
(2)在最大迭代次数内(MAXITER)运行算法,计算算法的收敛率(算法达到函数收敛精度的次数与总共运行次数的比值);

图3 基于ER模型演化机制结构平均度与熵值关系Fig.3 Relation between average degree and entropy of structure based on ER network evolution mechanism

图4 基于ER模型演化机制结构平均度和算法收敛率的关系Fig.4 Relation between average degree of structure based on ER network evolution mechanism and the rate of convergence of MABC algorithm
由图3可知,当平均度为0时,结构熵值为0,表明结构无信息转移能力。随着结构平均度的增大,结构的信息转移能力增加且在平均度大约为2时达到最大,此时结构的异质程度达到最大。而在平均度为2-7的区间内,虽然熵值有所下降,但是下降幅度较小,几乎接近最大熵值。在平均度大约为25度左右时,熵值达到谷底。此后,熵值开始逐渐增加,在平均度大约为48时再次达到最大。然而在平均度为49时,熵值突然降到最低值0.结构的信息转移能力正比例于结构的熵值。从图4可知,当平均度为0时,算法收敛率SR=0.随着平均度的增大,算法收敛率SR迅速增长,当平均度大约为6-7时,收敛率SR达到最大值。此后直到平均度为50时,算法始终保持相同的收敛率。当平均度为0时,由孤立节点组成的结构,虽然所用资源最少,但微粒间无任何信息的传递与共享,导致算法无法搜索到全局最优解。随着一些边的加入,结构转移信息的能力有所增长,各别微粒间存在信息的传递与共享,收敛率SR开始增加,当平均度达到大约6-7度时,结构信息转移的能力几乎达到最大,而算法收敛率SR也达到了最大值。因此,基于ER随机网络模型演化机制以概率(结构平均度为7)进行结构演化所获得的结构为MABC的最优种群结构。
5 仿真实验
为了验证上述最优种群结构的性能,选择了4个经典函数对在最优种群结构和完全种群结构下算法性能进行了评价。实验环境为种群规模N=50,所有函数维数n=50.算法停止准则为最大迭代次数,即MAXITER=6 000.实验数据均源于算法独立运行20次的平均抽样。
(1)Rosenbrock函数,单峰函数,在xi=1达到最小值0.
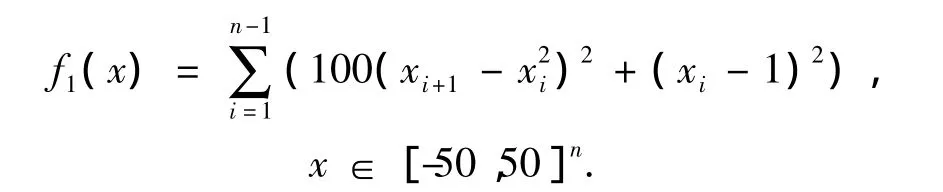
(2)sphere函数,单峰函数,在xi=0达到最小值0.

(3)Schwefel Problem 2.26函数,多峰函数,在xi=(420.968 7,…,420.968 7)达到最小值 -418.982 9n.
(4)Griewank函数,多峰函数,在xi=0大到最小值0.


表1 在最优结构平均度7和完全连接结构平均度49下MABC算法性能Tab.1 Performances of MABC in the optimal structure with average degree 7and full-connected structure with average degree 49
从表1可知,基于ER随机网络模型的演化机制,在结构平均度为7和49时算法具有几乎相同的性能,而平均度为7时结构中边的数量远小于平均度为49时,即仅需要较少的资源就可以使MABC算法获得好的性能,且此时的结构具有较强的信息转移能力,即较大的结构熵值。仿真实验再次表明了基于ER随机网络模型的演化机制以概率P=(结构平均度为7)进行结构演化所获得的结构为MABC算法的最优种群结构。
6 结论
本文采用SANTHOJI提出的方法论研究了一种改进ABC算法(MABC)的最优种群结构。研究表明基于ER随机网络模型演化机制以概率P=(结构平均度为7)进行结构演化可获得MABC算法的最优种群结构。也就是说,当结构平均度为7时,结构具有较强的信息转移能力,同时算法可以获得较好的性能。
[1]JEONG H,TONLBOR B,AIBERT R,et al.The1argescale organization of metabolic networks[J].Nature,2000,407:651-654.
[2]JEONG H,MASON S,BARABASI A L,et al.Lethality and centrality in Protein networks[J].Nature,2001,411:41-42.
[3]ERDOS P,RENYI A.On the evolution of random graphs[J].Publications of the Mathematical Institute of the Hungarian Academy of sciences,1960,5:17-61.
[4]WATTS D J,STROGATZ S H.Collective dynamics of‘small-world’networks[J].Nature,1998,393:440-442.
[5]BARABASI A L,ALBERT R.Emergence of scaling in random networks[J].Science,1999,286:509-512.
[6]穆华平,曾建潮,焦长义.基于小世界邻域结构的微粒群算法研究[J].太原科技大学学报,2009,30(1):7-11.
[7]SANTHOJI KATARE,DAVID H WEST.Optimal Complex Networks Spontaneously Emerge When Information Transfer is Maximized at Least Expense:A Design Perspective[J].Nature Physics,2006,11:26-35.
[8]PHAM D T,KOG E,GHANBARZADEH A,et al.The Bees Algorithm-A Novel Tool for Complex Optimisation Problems[C]//IPROMS 2006 Proceeding 2nd InternationalVirtual Conference on Intelligent Production Machines and Systems.Oxford,England:Elsevier,2006:231-235.
[9]KARABOGA D.An Idea Based on Honey Bee Swarm for Numerical Optimization[R].Tvrkey:Rciyes University,Engineering Faculty,Computer Engineering Department,2005.
[10]徐卫滨.无选择策略的改进蜜蜂群算法[J].太原科技大学学报,2011,32(5):343-346.

