基于信标节点间距离的改进RSSI定位算法

冯爱丽，乔钢柱，曾建潮

(太原科技大学计算机科学与技术学院，太原030024)

随着经济的发展和科学技术的进步，无线传感器网络[1]在安全生产、交通管理、医疗设备及智能家庭中得到了越来越多的应用，无线传感器节点功耗小、成本低、可靠性高，可以方便地布置在各种生产、生活需要的地方[2]。在利用无线传感器采集数据的时候，数据的来源地是一个我们需要获得的一个重要信息，没有位置信息的数据往往是没有意义的[3]，如煤矿事故人员搜救、车辆跟踪、温度测量等，所以精确定位对无线网络的应用有非常重要的意义。

定位方法总体上分为两大类，基于测距(rangebased)算法与非基于测距(range-free)算法[4]。非基于测距的算法无需测量节点间的距离，根据网络连通度估计未知节点的位置[5];基于测距的算法则通过测量未知节点与信标节点的距离或角度，再利用三边测量，三角测量，极大似然等算法计算节点的位置信息[6]。目前，测量节点间距离的方法[7]有RSSI、TDOA、TOA、AOA 等，RSSI是通过测量信号在空气中传播损耗来获得节点间的距离信息，所以RSSI测距[8]无需增加额外的硬件设备，节约成本，简便宜行，适合无线传感器趋势发展需要，因而得到了广泛的应用。但由于空间中物体、建筑墙壁引起信号的反射、多径效应及障碍物阻挡等问题，使测量到的RSSI产生波动，从而引起测量距离误差[9-10]。为了提高定位精度，必须提高节点间距离估计的准确性，距离由RSSI值计算得来，所以首先需要选择受环境干扰小的RSSI.本文通过把所测量的每个RSSI值与平均RSSI值进行比较，去除波动较大的数据，即受移动物体影响，严重失真的RSSI值，使所选择的RSSI值可靠性更高。再基于信标节点间的固定距离及所测量的RSSI信息，计算信标节点与未知节点的距离，通过仿真与一般平均值距离估计方法进行比较，最后结果表明本文算法提高了距离估计精度。

1 RSSI测距模型

目前有三种信号传输模型[11]:Free-Space模型、Two-Ray Ground Reflection模型和Shadowing模型。其中 Free-Space模型与Two-Ray Ground Reflection模型属于圆形信号传输模型，即信号传输模型是一个理想圆。由于信号在传输的过程中的多径效应以及障碍物阻挡等影响，使得传输模型显示出各向异性的特征，因而具有综合性的Shadowing统计模型在无线传感器网络的测距中得到了更广泛的应用。

Shadowing模型由两部分组成:第一部分为损耗模型(Pass Loss)，该模型用一个已知距离r0及此距离上的接收功率P(r0)为参考，可以预测出距离为r时的平均接收功率P(r)，损耗模型为:

其中n为路径损耗系数，是经过实际测量得到的经验值，范围在2～6之间，n值随着障碍物的增多而增大。

Shadowing模型的第二部分反映的是在固定距离上，接收能量符合对数正态随机变化，以dB为单位的Shadowing模型满足高斯分布，公式为:

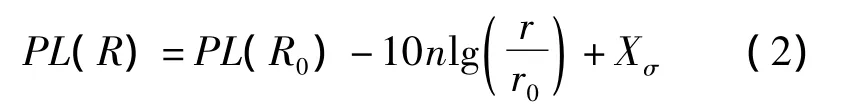
Xσ是一个零均值的高斯随机变量，实验证明对距离的计算结果影响不大，因此本文用去除Xσ的简单信号传输模型来估计距离。

2 算法模型

2.1 优选 RSSI值

定位准确的先决条件是有精确的节点间距离信息，而距离由接收到的RSSI值通过信号传输模型计算得到，所以选择能准确反映节点间距离的RSSI值至关重要。RSSI受多种因素影响，图1是由Shadowing模型得到的RSSI与距离的关系图。

图1 距离与误差的关系Fig.1 The relationship between distance and RSSI

由图1可知，RSSI值随距离的增加而减小。当距离比较近时，RSSI随着距离的增加而减小的很快，但当距离比较远时，距离的变化对RSSI的影响很小，所以距离越近，得到的RSSI值与距离的对应关系越准确。然而，RSSI值在受随机因素影响产生小幅度波动的同时，还会受移动物体的影响，产生大幅度波动，使所测量的部分数据严重失真，传统计算距离采用的是测量得到的多个RSSI的均值，如果把严重失真的数据用在均值计算RSSI上，得到的RSSI值不能准确的反映真实距离信息，因而需要去除严重失真的数据，提高定位精度。在实际环境中，如果没有移动物体的干扰，同一个信标节点在距未知节点相同的距离上所测得的RSSI值波动不大。所以本文引入了利用平均值去除严重失真数据，如果 RSSI与的差的绝对值与RSSI的比值超过所设定比率R时，就认为这个值属于严重失真数据，波动范围在R以内的值认为是正常环境中测量得到的值，可以保留，最后对保留的RSSI值求平均值，传给未知节点用来计算距离，求平均值与选择RSSI值公式如式(3)和式(4):

公式中R是通过大量实验测得的比率，它将使几乎所有在随机因素影响下的波动RSSI值包含在内。

2.2 RSSI测距改进模型

一个实际存在的网络中，不同位置的节点所处的环境不同，受到的干扰也不同，结果会产生不同距离上测到的RSSI值相同的情况，如果直接代入式(2)计算距离会产生误差，所以在计算距离时，应该引入环境因素的影响，使所获得的距离更准确。本文引入相似环境中其他信标节点的信息来改进估计距离，在式(2)中引入固定参考节点间的距离与平均RSSI值作为参考来校正RSSI值与距离的对应关系。

RSSIij表示信标节点Ai接收到邻近信标节点Aj的平均信号强度值，rij表示信标节点Ai与Aj之间的距离，RSSIi表示未知节点接收到的信标节点Ai的RSSI平均值，ri(j)表示以信标节点Aj为参考计算得到的未知节点与信标节点Ai之间的估计距离，代入式(2)，忽略高斯随机变量Xσ得:

由式(5)可得ri(j)的值。传感器网络中，节点部署一般比较密集，一个信标节点可以同时接收到附近多个其他信标节点的信号。由于距离越近，RSSI值与距离的对应关系越准确，所以为了使所选取的RSSIij与rij具有更好的参考价值，只选取离Ai最近的三个信标节点作为参考，计算ri(j)，然后取平均作为未知节点与信标节点Ai之间的估计距离:

实验结果表明，选择三个信标节点作为参考，已经可以明显减小估计距离的误差，同时减小了传感器节点的运算量，很好的满足了传感器适时性、耗能小的特性要求，使该算法能够更好地应用在传感器定位的实践中。

3 仿真实验及结果分析

利用MATLAB做算法仿真，仿真环境为40 m×50 m的区域，选取该区域的左下角坐标为(0，0)，右上角坐标为(50，40)，信标节点以横坐标上间隔10 m、纵坐标上间隔20 m的距离均匀部署，路径损耗系统设为2.9，通信半径设为50.

先做实验选择合适的R值，信号强度是服从高斯分布的Shadowing模型，这些信号强度只受随机因素影响产生波动，所以认为这些RSSI值都是在正常环境测量得到的值，选择的R值应该使这些值都包含在内。每隔1 m的距离上都连续采集50个RSSI值，求每个距离上最大的RSSI误差值与平均值比率，仿真结果如图2所示，由图2可知，最大误差比率不超过0.13，考虑真实环境中影响信号波动因素多，信号波动会更大，取R为0.2.

再把以平均值为基础的波动排除失真数据算法与信标节点参考算法结合仿真，与传统的取参考距离(r0)为1 m的平均值距离估计算法进行比较，仿真比较如图3所示。

图3中实曲线代表传统的均值算法仿真结果，虚曲线是采用改进RSSI算法仿真的结果，由图3可以看出，本文的改进RSSI算法明显提高了距离估计的准确性，在25 m内，距离估计误差在1 m以内，在50 m内，最大的距离估计误差约3 m，且大部分的距离误差都在2 m以内，这对未知节点的准确定位提供了保证。

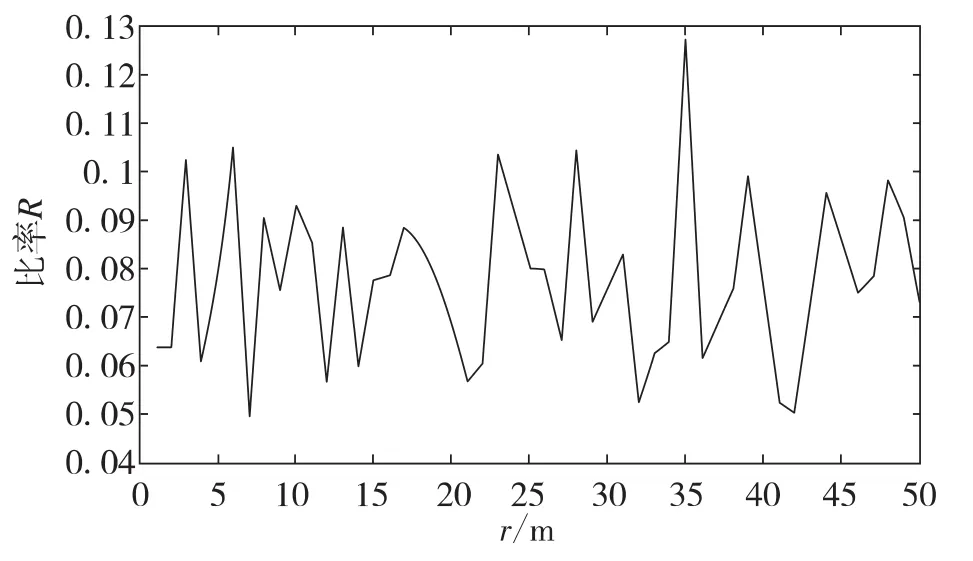
图2 不同距离上最大RSSI误差值与平均值的比率Fig.2 The ratio of the largest RSSI error and the average in different distance

图3 改进RSSI算法与传统均值算法的比较Fig.3 The comparison of improved RSSI algorithm and traditional average algorithm

4 结论

根据室内定位环境复杂，易受移动障碍物影响等因素，提出了优选RSSI值的平均距离波动消除法，消除严重失真数据，保留与距离关系对应好的RSSI值，再利用相似环境中其他信标节点间的距离及RSSI值来校正未知节点与信标节点之间的测量距离，从而有效的去除了所测量RSSI值中受移动障碍物影响较大的数据，消除了不同位置时环境参数不同对测距精度的影响。通过实验证明，本文提出的算法适合无线传感器网络室内定位，能够实现能耗低、定位精度高的要求。

[1]张宏巍，徐玉斌.一种无线传感器网络低延时信道接入协议[J].太原科技大学学报，2011，32(1):6-10.

[2]CHEN KAI，ZHOU YI，HE JIANHUA.A localization scheme for underwater wireless sensor networks[J].International Journal of Advanced Science and Technology，2009(4):9-16.

[3]李白莉，徐玉斌，李俊吉.改进DV-Hop定位算法在随机传感器网络中的研究[J].太原科技大学学报，2011，32(2):85-88.

[4]王博，徐玉斌.无线传感器网络中节点的非测距定位算法[J].太原科技大学学报，2009，30(6):466-470.

[5]BULUSU B，HEIDEMANN J，ESTRIN D.GPS less low cost outdoor localization for very small devices[J].IEEE Personal Communications，2000，7(5):28-34.

[6]RUDAFSHANI M，DATTA S.Localization in wireless sensor networks[C]//Proceeding of the 6th International conference on Information Processing in Sensor Networks(IPSN)，USA:NY，ACM，2007:51-60.

[7]孙立民，李健中，陈渝，等.无线传感器网络[M].北京:清华大学出版社，2005.

[8]ALIREZA N，JACEK I.A test bed for localizing wireless LAN devices using received signal strength[C]//Proc of the 6th Annual Communication Networks and Services Research Conf(CNSR2008)，Canada，Halifax，2008:481-487.

[9]LYMBEROPOULOS D，LINDSEY Q，SAVVIDES A.An empirical analysis of radio strength variability in IEEE 802.15.4 networks using monopole antennas[R].ENALAB Technical Report，2005.

[10]CHO H，KANG M，PARK J，et al.Performance analysis of location estimation algorithm in ZigBee networks using received signal strength[C]//Proceedings of the 21st International Conference on Advanced Information Networking and Applications Workshops，Niagara Falls，Ontario，2007，2:203-206.

[11]赵昭，陈小惠.无线传感器网络中基于RSSI的改进定位算法[J].传感技术学报，2009，22(3):391-394.

[12]乔钢柱，曾建潮.一种适用于动态环境的改进RSSI定位方法[J].计算机研究与发展，2010，47(Suppl.):111-114.