基于APDL的汽车起重机伸缩臂参数化分析
程 鹏,韩 刚,樊 涛
(太原科技大学机械工程学院,太原030024)
伸缩臂是汽车起重机最为重要的部体,其重量约占整机的20%~30%,减轻吊臂重量,增大吊臂刚度是改善汽车起重机性能的重要途径,因此,需要对吊臂进行受力分析,找到其最不利受力位置,并对此进行改善。利用静态有限元分析可以对结构进行强度和刚度校核[1],ANSYS提供的APDL语言是一种可实现人机交互的汇编语言,应用APDL语言编写对起重机伸缩臂进行建模和受力分析的控制程序,通过宏命令操作实现对起重机伸缩臂的参数化,方便快捷的进行起重机的设计和分析,避免了传统设计和校核中重复计算带来的麻烦。
1 有限元模型建立
ANSYS软件提供了两种工作模式,人机交互(GUI方式)和命令流方式(BATCH方式)。通过GUI方式进行的每一步工作流程都会通过APDL语言在logfile文件里留下轨迹,方便修改和提取信息。因此对于分析类型和计算方法相同的模型,可以通过APDL语言编写命令流在ANSYS中进行运算[2-4]。在软件前台的人机界面中,可通过改变不同的参数大小而实现用户所需要的理想模型尺寸和分析类型。
汽车起重机伸缩臂的截面形状有很多种,主要根据受力情况和作业工况确定,包括矩形、梯形、六边形、八边形、十二边形、U形和椭圆形。本文主要对六边形截面、U形截面和椭圆形截面进行分析,如图1所示。通过不同工况下臂架的受力和变形情况,分析出滑块长度和臂架搭接量对伸缩臂的影响,并且实现三种截面的臂架在不同工况下受力情况的对比,找到最合理的截面形状。
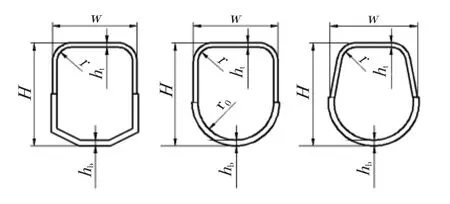
图1 矩形,U形和椭圆形截面示意图Fig.1 Schematic diagram of rectangular,U-shape and oval section
在建模中,臂长、截面尺寸、滑块尺寸和钢板属性等参数都是需要控制的建模参数,滑块的单元类型选择为solid45,钢板的单元类型选择为shell63,模型的上盖板厚度ht和下盖板厚度hb通过常数来改变。由于伸缩臂只与滑块在伸缩方向有相对滑动,故其他5个自由度需要通过耦合来约束。本模型主要通过选择接触面节点,应用cp命令实现接触面的耦合,这种耦合比建立接触对的方式简便,并且应用线性计算方法,拥有计算量小、计算速度快和计算精确的优点[5]。为了保证焊接工艺而设计的边缘加强部分对计算结果影响很小,所以建立有限元模型时进行了简化。臂头加强筋和臂根加强板均由面代替,只是适当增加了面的厚度。实际臂根与转台铰接处由于筋板较多,受力比较复杂,所以也简化为一个被加厚的面,这与实际受力和约束条件相符,计算也相对准确[6]。臂架焊缝选择在臂架高度的中分面上,滑块和盖板都是比较规则面,网格划分时采用映射网格划分方式,这样可以增加划分的速度,并能在计算中减少迭代次数。在液压缸铰点处和臂根铰点处建立刚度节点,并且在这些节点处约束臂架的自由度UX、UY、UZ、ROTY和ROTZ,只释放臂架绕铰点转动的自由度。
2 载荷分析与臂架尺寸确定
2.1 载荷分析
汽车起重机的起重量是随幅度的变化而变化的,其工作级别为A3-A6,在小幅度时,起吊能力是由臂架强度决定,而大幅度时是由起重机整机稳定性决定的,因此,汽车起重机伸缩臂一般可不验算疲劳强度,只需按最小幅度起吊最大载荷来作强度计算[7]。汽车起重机臂架上所受的载荷有起升载荷、臂架自重、惯性载荷及风载荷等,按受力分析可将这些载荷分解为轴向力和横向力。
在吊臂的变幅平面内,吊臂受到的载荷为:
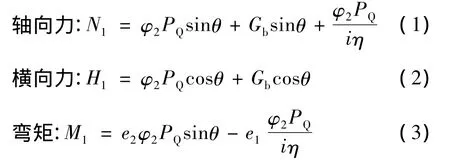
在吊臂回转平面内,吊臂受到的载荷为:

式中,i——吊钩滑轮组的倍率;
η——滑轮组效率;
φ2——起升动载系数;
φ5——动力效应载荷系数;
θ——吊臂仰角;
PQ——额定起升载荷,PQ=(mQ+m0)g;
g——重力加速度;
mQ——变幅平面起升质量;
m0——吊具自重;
Gb—— 臂架自重,Gb=mbg,mb为臂架质量;
α——起重机钢丝绳最大偏摆角,取3°~6°;
aτ——臂架端部的切向加速度;
e1,e2——起升绳导向滑轮轴心和吊钩定滑轮轴心到吊臂中性轴线的距离;
PW——作用在起重机上的工作状态最大风载荷。
2.2 臂架尺寸确定
以50吨汽车起重机伸缩臂为例,通过经验公式计算截面的基本参数,然后以QY-50汽车起重机节臂尺寸为参考,确定最大主臂长度为38 m;基本臂至五节臂长分别为:9.630 m、9.537 m、9.192 m、8.906 m、8.901 m;最小搭接长度分别为 2.714 m、2.369 m、2.083 m、1.954 m;确定液压缸铰点离臂根铰点的距离为基本臂的一半。QY-50汽车起重机臂架材料采用BS700,屈服强度σs为700 MPa,强度极限σb为800 MPa,取安全系数为1.33,则钢板的最大许用应力为526 MPa[8]。以起重机伸缩臂全展开,在最小幅度,仰角78°,起重量8.5 t时的工况进行分析时,六边形、U形和椭圆形的最大应力分别为304 MPa,306 MPa和288 MPa,且均出现在液压缸与基本臂铰接处,这符合实际情况,故三种截面臂架的最大应力均满足强度要求。在此工况下,三种截面吊臂的最大位移分别为855 mm,729 mm和922 mm,而38 m吊臂的最大挠度[f]=L2/1 000=1 444 mm,故三种截面臂架满足刚度要求。
椭圆形截面伸缩臂在高度和宽度不变的条件下,截面下部椭圆部分的纵坐标可以改变,并且臂架最大应力与椭圆纵横坐标比值有一定关系,如表1所示。从表中可以看出臂架最大应力先随椭圆纵横坐标比值增大而减小,当比值为1.2时出现最小值,之后又呈增大趋势;而最大位移随比值增大而增大,并且均小于许用挠度,说明在椭圆纵横坐标比值为1.2时为椭圆形截面最优形式,即椭圆长短轴之比为1.2时,椭圆形截面伸缩臂所受的最大应力最小。

表1 椭圆纵横坐标之比与臂架最大应力和最大位移关系Tab.1 Relationship between the ratio of vertical and horizontal ordinates in elliptic coordinates and the maximum stress and maximum displacement of telescopic jib
3 滑块、搭接量和截面形状对臂架的影响
3.1 滑块对臂架的影响
滑块是连接各节臂的重要部件,滑块和臂架间的接触面积对臂架与滑块接触处的应力有很大影响。以一二节臂搭接滑块的上滑块处为例,当滑块宽度和高度不变的情况下,滑块长度大小将会影响臂架与滑块接触处的最大应力,如图2所示。

图2 滑块长度与搭接处臂架最大应力关系Fig.2 Relationship between slider length and maximum stress on overlap place
从图2中可以看出,滑块长度与臂架搭接处最大应力间呈现出近似指数的关系,并且为指数下降的趋势,即在滑块长度较小的情况下滑块与臂架搭接处的应力将会非常大,而且已经超过臂架的最大许用强度,而随着滑块长度增大,最大应力不断下降,到达一定长度时又趋于平稳。三种截面的这种趋势基本相同,拐点均出现在滑块长度为100 mm~200 mm的地方。在起重臂的装配和调试阶段,根据滑块与臂架接触处应力的变化所确定的滑块长度情况将会在很大程度上决定起重机实际的大吨位高起升高度工况下起吊重物的能力。
3.2 搭接量对臂架的影响
在吊臂仰角和幅度不变的情况下,各节臂间的搭接量与臂架所受最大应力和臂架最大变形间存在一定关系。随着臂架间搭接量的减小,臂端到变幅液压缸铰点的距离会增长,所以在变幅液压缸铰接处的弯矩会增大,而臂架最大应力就发生在臂架与变幅液压缸铰接处,所以臂架最大应力会随臂架间搭接量的减小而增大;而臂架的最大位移会出现在伸缩臂臂端,因此总位移也会随搭接量的减小而增大。以U形截面的臂架为例,如图3,图4所示。臂架最大应力在搭接量为4 000 mm~8 000 mm时比较小,而最大变形在搭接量为5 000 mm~7 000 mm时趋于平缓,所以综合应力和变形的关系,采用同步伸缩方式工作的汽车起重机在满足起升高度的情况下,各节臂搭接量为臂架长度一半以下时比较合理,并且对臂架内液压缸的使用寿命也比较有利。

图3 各节臂间搭接量与臂架最大应力关系Fig.3 Relationship between overlap length and maximum stress of arms
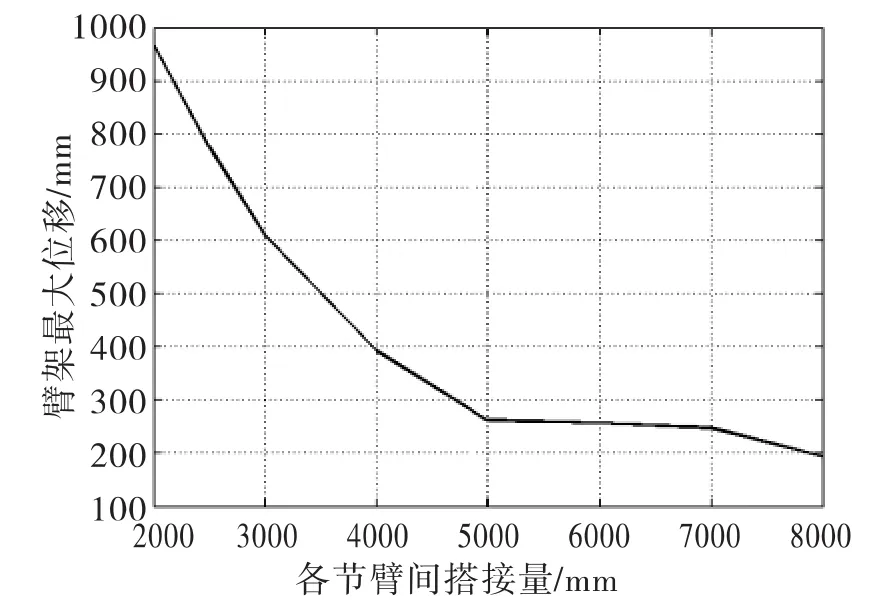
图4 各节臂间搭接量与臂架最大位移关系Fig.4 Relationship between overlap length and maximum displacement of arms
3.3 截面形状对臂架的影响
汽车起重机在不同吊臂仰角工作时基本臂对变幅液压缸的压力是不同的,由于吊臂的最大应力出现在基本臂与变幅液压缸铰接处,所以这种不同体现为不同吊臂仰角与臂架最大应力和最大位移的关系,如图5,图6所示。
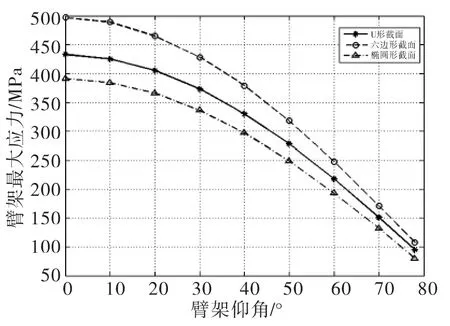
图5 臂架仰角与最大应力关系Fig.5 Relationship between angle of elevation and maximum stress of arms
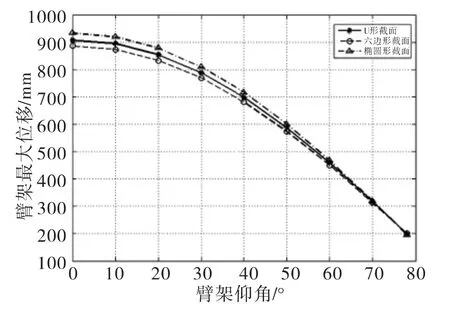
图6 臂架仰角与臂架最大位移关系Fig.6 Relationship between angle of elevation and maximum displacement of arms
起吊相同吨位时,随着吊臂仰角的增大,三种截面臂架的最大应力和最大位移都在减小。在整个仰角变化过程中,椭圆形截面臂架应力一直最小,U形截面次之,六边形截面臂架应力最大;臂架最大位移随臂架仰角变化时三种截面臂架的最大位移差距不大,在臂架最大仰角时三种截面臂架的最大位移基本相同,并且都满足许用挠度的要求。这说明椭圆形截面吊臂受力最合理,并且椭圆形截面的重量最小,材料利用最充分,所以在大吨位的汽车起重机中椭圆形截面的综合性能最好。但是受工艺的限制,椭圆形截面加工比较困难,所以U形截面在大吨位汽车起重机中比较常见,六边形截面主要应用于中小吨位中。
4 结束语
通过ANSYS提供的人机交互平台,应用APDL语言实现了对汽车起重机伸缩臂的参数化设计,并且应用吊臂的应力和变形情况,分析滑块、搭接量和截面形状对臂架的影响。通过对几种不同截面形状臂架的强度和刚度对比,找到了最有利的伸缩臂截面形状。这种应用ANSYS软件对伸缩臂的参数化分析解决了在传统设计中重复计算的问题,找到了一种适合设计人员对汽车起重机吊臂快速分析的方法。
[1]侯晓望,童水光.基于有限元分析的液压机构优化[J].重型机械,2005(4):46-48.
[2]李峰,崔志远,韩刚.基于ANSYS的传动滚筒的有限元分析[J].太原科技大学学报,2007,28(4):307-310.
[3]李海虹,陈永会,李志潭,等.利用有限元进行塔机起重臂的动态分析[J].太原重型机械学院学报,2003,24(2):106-109.
[4]杨成云,林腾蛟.中心传动齿轮箱体有限元分析及结构优化设计[J].重型机械,2001(2):42-45.
[5]高原.基于APDL的起重机伸缩臂参数化设计与分析[D].大连:大连理工大学,2010
[6]曾成奇.起重机伸缩臂结构优化设计及有限元分析[D].太原:太原科技大学,2010.
[7]焦文瑞,孔庆华.汽车起重机箱形伸缩式吊臂的有限元分析[J].工程机械,2007,38(9):33-36.
[8]纪爱敏,彭铎,刘木南.三种工况下大型吊臂的有限元分析[J].工程机械,2006,37(2):30-33.

