基于宏、细观模型的疏松缺陷研究方法
吴永强,安红萍
(太原科技大学材料科学与工程学院,太原030024)
疏松缺陷是在钢锭凝固过程中不可避免的现象,在热成形过程中若不能有效控制,将会严重降低锻件的使用寿命甚至使锻件报废。长期以来,国内外学者对锻造过程中存在疏松缺陷的的演变及控制做了大量的研究,总结出疏松缺陷闭合的规律和提出疏松缺陷闭合的变形临界条件,为制定合理的锻造工艺提供可靠依据[1]。有限元数值模拟方法是研究疏松缺陷闭合的常用方法,它即能够获得塑性加工制品内部疏松缺陷的闭合过程,又能够获得影响其闭合过程相应的变形条件(温度、应变速率等参数)。事实上,大锻件与其内部存在的疏松缺陷尺寸相差悬殊,利用有限元分析软件在相对较大的工件中很难作出尺寸很小的疏松缺陷,即疏松缺陷尺寸大小与整体工件尺寸大小比例条件达不到实际生产条件,数值模拟分析的精确性受到质疑。很多研究者利用有限元数值模拟方法对锻件内部存在的孔洞闭合现象进行了模拟计算,例如:清华大学王祖唐利用数值模拟的方法对大型锻件孔洞闭合过程进行分析,并利用钢坯内人工造孔及划刻网格的方法进行数据分析得出孔洞沿最大压应变方向闭合的结果[2-3];崔振山、任广升等用刚塑性有限元的数值模拟和塑泥试样的物理模拟分析了在镦粗过程中工件内部孔洞缺陷演化过程,得到孔洞周围存在一个应力应变集中区域,并且应变集中程度随着孔洞尺寸的变小而越剧烈[4-5];西北工业大学吕毅利用有限元计算细观力学法(有限元法、细观力学和材料科学相结合的方法)做了《基于有限元计算细观力学的复合材料宏观性能一体化预测》,该课题的方法关键是以先进的前后处理软件MSC.PATRAN-R2为平台,在该平台上用 PCL(patran command language)为开发工具建立合适的代表性特征体积元(RVE),实现了代表性特征体积元(RVE)参数化自动建模,建立了代表性特征体积元(RVE)库[6]。
本文针对代表性特征体积元(RVE)施加适当的边界条件进行有限元数值模拟分析,利用代表性特征体积元(RVE)应力应变场对宏观锻件内部疏松缺陷的闭合行为进行预测,为以后根据温度、应变速率、疏松缺陷大小合理制定在锻造过程中相应的工艺参数做准备,以及为制造质量优良的塑性加工制品提供帮助。
1 宏、细观模型的建立
疏松缺陷的变形过程是由疏松周围基体材料的运动引起的,在塑性加工过程中由于外力加载,基体材料产生流动并填充到疏松缺陷中,疏松缺陷闭合。为分析疏松闭合过程建立宏观与细观两种尺度下模型,具体做法是首先通过有限元分析软件Deform-2D建立宏观模拟模型,而细观模型中代表性特征体积元(RVE)的边界条件从宏观模型中获得,宏细观两种尺度下的模型关系如图1所示。
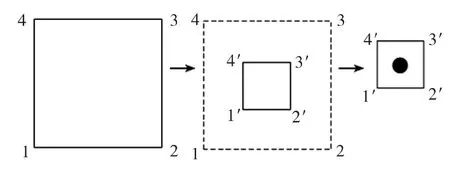
图1 宏细观模型关系Fig.1 The relationship between the macro model and the mesoscopic one
图2表示细观模型中代表性特征体积单元(RVE)由基体和疏松缺陷组成。这个代表性特征体积单元(RVE)处于无限大的基体之中,周围材料对它产生约束作用。提取宏观模型中特定点处的加载历史作为细观模型中代表性体积元(RVE)的边界条件,研究与宏观模型一致的变形过程中疏松闭合情况。通过一些简单的本构关系描述代表性特征体积单元(RVE)在变形过程中的行为(如:力学行为等),再用无数具有简单本构关系的小单元叠加就可以得到整个塑性变形工件的整体行为。

图2 含疏松的代表性特征体积单元Fig.2 The representative volume element with loose defects
2 边界施加方法
本课题研究的是利用细观模型再现宏观模型的变化过程,它的具体要求是在代表性特征体积元(RVE)上加载边界条件,使它在与宏观模型相同的时间内有相同的变形规律,即具有相同的等效应变、等效应变速率、平均应力等表征塑性加工制件在变形过程中的参数。基于宏观基体材料的细观结构周期性假设,选取适当的代表性特征体积元(RVE),在保证宏、细观模型之间能量等效前提下,采取弱化的连续性边界条件以及周期性边界条件,建立和求解细观力学方程。借助均匀化理论将大量代表性特征体积元(RVE)的表征参数平均化,建立宏观与细观两种尺度坐标范围内的一系列方程,得到宏观和细观两种某表征参数下的细观场表达式。在有限元分析软件Deform-2D中,代表性特征体积元(RVE)的边界条件从宏观模型中获得,为保证边界条件数据传递的正确性,本文做了大量的边界条件加载方案,最后得到了可行性的方案[7-9]。下面列举本文做过的三种边界条件加载方案:
(1)在Deform-2D软件中建立宏观模型,选择特征单元,提取表达其变形历史的应力-时间及速度—时间数据作为细观模型的边界条件,建立如图2所示的含有疏松缺陷的细观模型(为简化取1/4分析),如图3所示。
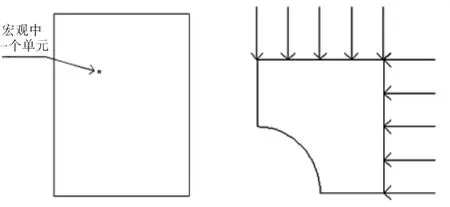
图3 方案一:代表性特征体积元的四分之一Fig.3 Scheme one:One quarter of the representative volume element
在代表性特征体积元(RVE)的1/4的上边和右边同时加载应力边界条件或者同时加载速度边界条件;或者在代表性特征体积元(RVE)的1/4的上边加载应力边界条件右边加载速度边界条件;或者在其上边加载速度边界条件右边加载应力边界条件。而在以上所有加载方法下代表性特征体积元(RVE)的1/4模型的下边和左边总是加载应力边界条件使细观模型固定。实验结果是代表性特征体积元(RVE)变形的有关参数(等效应变、等效应力、平均应力等)是宏观模型的对应参数的几倍甚至是十几倍,即从宏观模型提取的边界条件加载到细观模型的数据传递不准确,细观模拟过程不能完全再现宏观模拟过程。宏观工件中右上角一点与在用该方案加载边界条件的代表性特征体积元(RVE)中等效应变在同一时刻的相对误差值如表1所示:

表1 相对误差百分比Tab.1 The relative error percentage
(2)与方案一相同,选择宏观模型中的单元提出其变形历史构建细观模型。不同之处为在代表性特征体积元(RVE)的四边同时加载应力边界条件或者同时加载速度边界条件;或者采用上边和右边加载应力边界条件,左边和下边加载速度边界条件的混合加载方式。有限元模拟结果是代表性特征体积元(RVE)变形的有关参数(等效应变、等效应力、平均应力等)逐渐接近宏观模型相对应参数,即从宏观模型提取的边界条件到代表性特征体积元(RVE)的数据传递准确性提高如表2所示,但细观模拟过程还不能完全准确再现宏观模拟过程如图4所示。

表2 相对误差百分比Tab.2 The relative error percentage
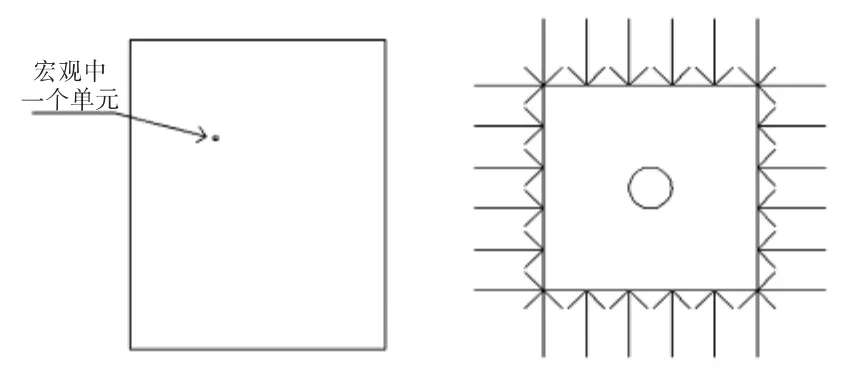
图4 方案二:对整个单元进行加载Fig.4 Scheme two:the loading of the whole element
(3)建立宏观模型,选择特征节点,提取表达其变形历史的应力-时间及速度—时间数据作为细观模型的边界条件,由于宏观模型比代表性特征体积元(RVE)的尺寸大很多,宏观模型中这个点可视为一个微小的含缺陷区域。在建立细观模型时可不再拘泥于宏观模型中单元的尺寸大小如图5所示:
为了方便有限元模拟分析把细观模型尺寸定位1mm×1mm.在进行边界条件加载时如图6所示黑色箭头表示该代表性特征体积元上(RVE)加载的是速度边界条件,红色横线表示该代表性特征体积元(RVE)加载的边界条件是应力边界条件,中间位置紫色短道横线表示疏松缺陷锻合完毕后状态。

图5 方案三:宏观模型中取其中一点Fig.5 Scheme three:one point in the macroscopic model
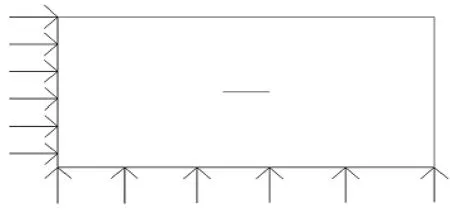
图6 加载方案Fig.6 The loading project
在有限元分析软件Deform-2D中,在加载边界条件时,边界条件的加载间隔步数过大容易使刚开始几步的表征变形参数(等效应变、等效应力、平均应力等)发生突变,与宏观模型相应参数相差很大。故不采用等间隔步数加载边界条件,而使前几步加密处理,让边界条件加载的间隔步数减少。宏细观边界条件数据传递准确性的证明如图7所示,其中纵坐标误差百分比即相对误差百分比。
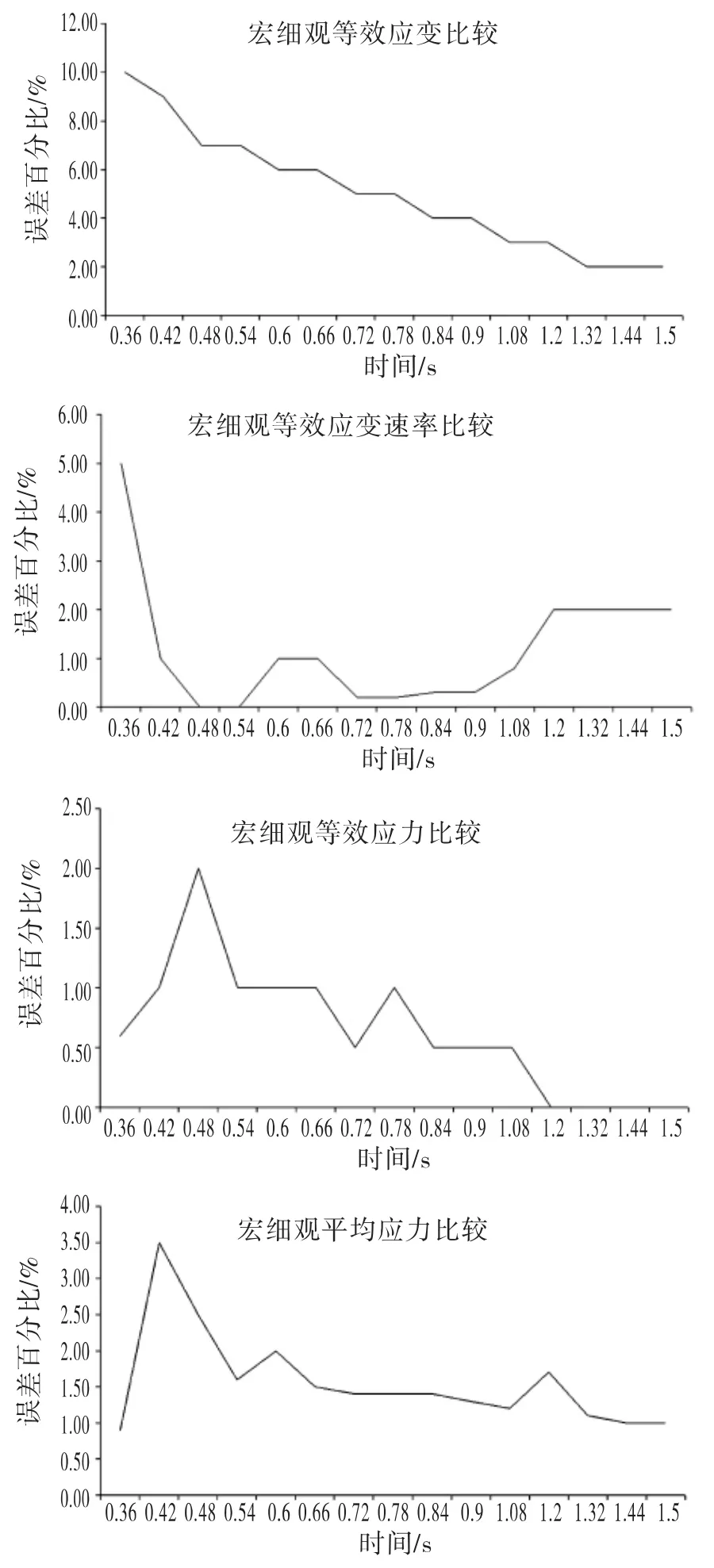
图7 传递中的误差Fig.7 The error in transfer process
综上,采用方案三即采用左边和下边加载速度边界条件,上边和右边加载应力边界条件,该方案有限元模拟出来的代表性特征体积元(RVE)的表征变形参数(等效应变、等效应力、平均应力等)与宏观模型的相应表征变形参数非常接近,最大的误差为10%,当变形稳定后,大多数误差范围所在数量级为10-2,有的宏细观参数间误差甚至达到千分之几,即该细观模型的模拟过程可以再现宏观模型的变形历史,而且能够获得缺陷闭合过程。在建立正确的有限元数值模型后,研究者就可以根据此方案在不同的温度、应变速率、疏松缺陷尺寸大小条件下进行模拟分析,为消除锻件内部疏松缺陷和制定合理锻压工艺提供依据[10]。疏松缺陷闭合时形状变化过程如图8所示。
图8 疏松缺陷的闭合过程Fig.8 The closing process of the loose defects
4 结论
本文基于有限元分析软件Deform-2D在宏细观两种尺度下建立模型,细观模型为含有疏松缺陷的代表性特征体积元(RVE),通过在其上施加适当的边界约束条件和载荷,使从宏观模拟提取的边界条件数据恰当地施加到代表性特征体积单元(RVE)上,从而保证从宏观模型到细观模型数据传递的准确性即变形表征参数(等效应变、等效应变速率、等效应力、平均应力等)误差极小,这样就说明在锻造过程中细观模型的变形过程可以再现宏观模型中的某一单元变形过程。研究者在消除大型锻件内部存在疏松缺陷时,可以对工件中存在严重缺陷的某一小范围进行模拟分析以便制定锻造工艺,这样既节省了设计时间也减少了在对整个工件全部分析过程中带来的不准确性。
[1]郭会光,曲宗实.我国大锻件制造业的发展[J].大型铸锻件,2003(1):1-2.
[2]王祖唐,刘庄,任猛.大型钢锭内部空洞性缺陷锻合过程的实验研究[J].机械工程学报,1989,25(4):47-53.
[3]王祖唐,刘庄,任猛.大钢锭内部空洞锻合过程的数值模拟[J].机械工程学报,1989,25(3):51-55.
[4]任广升,谭红,李运兴.镦粗过程中锻件内孔洞缺陷邻域应变分布的模拟研究[J].塑性工程学报,1994,1(3):14-19.
[5]崔振山,任广升,徐秉业,等.圆柱体内部空洞的热锻闭合条件[J].清华大学学报,2003,43(2),227-229,233.
[6]吕毅,吕国志,孙龙生.基于有限元计算细观力学的RVE库的建立与应用[J].机械强度,2009.31(5):851-856.
[7]LUO CHUNHUI.Evolution of voids close to an inclusion in hot deformation of metals[J].Computational Materials Science,2001,21:360-374.
[8]LUO CHUNHUI,ULF STAHLBERG.Deformation of inclusion during hot rolling of steels[J].Journal of Materials Processing Technology,2001,114:87-97.
[9]LUO CHUNHUI.Modeling the behavior of inclusions in plastic deformation of steels[D].The doctor’s degree in KTH,2001.
[10]任运来.大型锻件内部缺陷修复条件和修复方法研究[D].河北秦皇岛:燕山大学,2003.
——勉冲·罗布斯达

