基于危险点分布比率-SVM分类的轨道不平顺峰值安全域估计

张媛 ，秦勇，贾利民

(1.北京交通大学 轨道交通控制与安全国家重点实验室，北京，100044；2.北京交通大学 交通运输学院，北京，100044)

轨道的平顺性直接关系到列车运行品质和轮轨间作用力，是引起机车车辆振动的主要根源，因此良好的轨道平顺状态是降低轮轨作用力、保证行车安全的重要条件[1-2]。近年来，随着铁路运行速度的不断提高，对轨道平顺性的要求也愈加严格。轨道不平顺的峰值是影响行车安全的重要因素[3-6]，也是各国现有轨道几何管理标准中评定轨道状态的基本指标[7]。迄今，国内外诸多学者均对轨道不平顺限值的确定方法进行了研究。练松良等[8]模拟仿真客货车动力系响应，归纳出了客货共运线路的轨道不平顺不利波长的范围；吴旺青[9]通过速度、不平顺幅值和波长等多种组合条件下的仿真，提出了秦沈客运专线综合试验段轨道不平顺管理标准建议值；李明华等[10]通过建立整车模型和对运动方程的求解，探讨了轨道高低不平顺对列车垂向加速度的影响，提出300 km/h速度时应满足的轨道最大高低不平顺幅值；Cheli等[11]分析了不同运行速度时不同波长的轨道不平顺对脱轨危险性的影响；Alfi等[12]基于数值实验，给出了一个波长大于20 m的长波不平顺估计方法；陈果等[13]建立了车辆/轨道垂横耦合模型。在充分考虑多种波长并存的情况下，仿真计算了250 km/h高速铁路各种轨道不平顺的管理目标值。这些研究对轨道不平顺及其影响进行了详细分析，但大都是分别考察某一速度下、某一类型或某一波长及某幅值范围内的轨道不平顺对车辆运行的影响，在各类型、各波长及各幅值的轨道不平顺耦合后其峰值对车辆整体运行状况的影响分析方面尚待深入，以更加全面准确地反映系统实际运行情况。本文作者从域的角度出发，采用2种不同水平轨道谱作为轨道激励，其中包含高低和轨向2种类型的多波长多幅值随机不平顺，克服了单一类型、波长或幅值的不平顺激励所得结果的限制性；搭建高速客车动力学仿真模型以采集轨道激励下的脱轨系数等安全性指标的值，根据一定的安全评判规则将轨道不平顺幅值数据标记到“安全”和“危险”2个区域；基于已有的标记数据，提出一种新颖的基于危险点分布比率的SVM不平顺幅值数据分类方法，得到了不同速度下高低和轨向两类不平顺峰值的安全域边界，可为高速铁路轨道不平顺幅值管理及标准制定提供参考。在理解轨道交通系统安全域概念的基础上，利用Simpack搭建了高速列车仿真模型获取了仿真数据，提出了采用基于危险点分布比率-SVM分类方法进行轨道不平顺峰值安全域估计，并进行了不同速度下轨道不平顺峰值安全域估计试验验证本文方法的有效性。

1 轨道平顺状态安全域

轨道交通系统中，安全域是从域的角度全面描述系统可安全运行区域的定量模型，安全域边界与系统运行状态点的相对关系可提供定量化安全裕度和最优控制信息，可满足精确安全状态信息分析和动态安全评价的高速铁路安全保障需求[14]。

本文中，就轨道平顺状态来说，其安全域即指可使高速列车运行时能够满足既定的安全性和舒适性要求的轨道不平顺幅值的范围，该范围的阈值即为本文中需估计的轨道不平顺峰值的安全域边界。

2 仿真模型建立及数据获取

2.1 高速客车车辆动力学仿真模型

基于多体动力学仿真软件Simpack建立了某高速客车的车辆动力学仿真模型。该客车可模拟成一个包括车体、2个转向架和4个轮对的多刚体系统，轮对通过一系悬挂与转向架构架连接，转向架通过二系悬挂与车体相连，车体与每个构架之间配有2个横向减振器、2个蛇形减振器及2个垂向减振器，且在构架和车体间设有弹性横向止挡。轨道设置为直线轨道，钢轨尺寸依据UIC60标准设置，轮轨接触模型采用单点弹性接触模型，即通过赫兹接触弹簧-阻尼系统计算轮轨接触力。

该模型考虑车体、构架、轮对等3个刚体的六方向自由度，共计42个；建模过程中考虑的作用力包括二系悬挂界面中的空气弹簧力、3种减震器阻尼力和横向止挡力，一系悬挂界面中轴箱弹簧力、轴箱定位装置力、减震器阻尼力，以及轮轨界面中的法向力、蠕滑力、蠕滑力矩[15]，其中轮轨界面中的轮轨力可由软件自动生成。此外，轨道激励可直接设置Simpack软件中轨道谱或采用导入时域数据的方法输入至仿真模型中。本文搭建的车辆动力学仿真模型如图1所示，经名义力计算验证了其合理性。

2.2 数据采集及预处理

为更加准确地模拟我国准高速及高速铁路轨道几何状况，获取合适范围和粒度的不平顺幅值数据，本文轨道激励设置为德国高速低干扰谱和美国六级谱，在2种不同水平的轨道平顺状态下分别进行了仿真试验，并将此2种激励信号下的试验数据合并处理。由于高低和轨向不平顺对车辆与轨道动力响应的影响显著[16]，因此，激励信号选择为2种轨道谱下的高低与轨向2种不平顺信号。

图1 高速客车车辆动力学模型Fig.1 High-speed passenger vehicle dynamics model

为了对轨道不平顺幅值进行“安全”与“危险”(即“超限”与“未超限”)标记，需要选取若干安全性指标用于评价车辆在某一轨道不平顺幅值下的运行状态。本文考虑发生爬轨、悬浮及钢轨挤翻等危险的可能性，选取常用的脱轨系数(Derailment coefficient,DC)、轮重减载率(Wheel load reduction rate, WLRR)以及轮轨横向力(Wheel-rail lateral force, WRLC)作为安全性评判指标，即仿真模型输出为脱轨系数、轮重减载率及轮轨横向力3个动力学响应信号。此外，考虑脱轨系数的持续作用时间问题，采用了UIC518中的2 m滑动平均方法[17]对脱轨系数进行了平滑处理；考虑对轮轨安全构成实质性威胁的是轮轨横向力中的低频部分，故采用4阶Butterfly型IIR 低通滤波器对其进行了0～40 Hz的滤波处理。

德国高速低干扰和美国六级2种轨道谱激励下的运行里程均为450 m，采样间隔0.5 m，将2种轨道谱激励下所采集到的数据共1 800对合并为1组。共采集了速度分别为200，240，280和320 km/h时的4组二维输入-三维输出数据对。图2所示为200 km/h速度下经上述预处理后的输入输出数据。图中前450 m的轨道激励为德国高速低干扰谱，后450 m的轨道激励为美国六级轨道谱。

图2 200 km/h时输入输出数据Fig.2 Inputs and outputs data at 200 km/h

3 SVM理论

支持向量机(Support vector machine，SVM)是在基于有限样本统计学习理论(Statistical learning theory,SLT)和结构风险最小化(Structure risk minimization,SRM)原则上发展而成的一种创造性机器学习方法[18]。SRM比传统的经验风险最小化原则(Empirical risk minimization, ERM)更优越，这使SVM具有更强的泛化能力[19]。由于SVM 有严格的理论和数学基础，不存在局部极小的问题，具有很强的泛化能力，能够较好地解决小样本、非线性、高维空间等机器学习中的难点问题，因此其广泛应用于模式识别、系统辨识和控制理论等领域[19-22]。

SVM的二分类问题就是寻找一个最优分类超平面，使得从这个超平面到2类样本中最近样本的距离之和，即分类间隔最大[23]。假定一个n维l个样本的矢量集

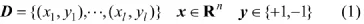
和一个n维的超平面

解矢量w*即为支持向量，它是一个由训练样本集的一个子集样本矢量构成的展开式。从训练集中得到了描述最优分类超平面的决策函数即支持向量机，它的分类功能由支持向量决定。决策函数可表示为

对于线性不可分问题，可以将待分样本通过非线性变换映射到某个高维的特征空间，如式(6)，使得其在该高维空间下线性可分。

即对于线性问题，核函数为2个向量的点积运算；而对于非线性问题，SVM的核心思想就是通过引入非线性映射，将输入向量映射到高维空间来构造最优分类面。目前，常用的核函数主要有多项式核、高斯径向基核、Sigmoid核和B-样条核等。

总之，SVM的形式类似一个神经网络，输出即为中间层节点的线性组合，每个中间层节点对应一个支持向量，如图3所示。

图3 SVM分类器示意图Fig.3 Schematic diagram of SVM classifier

采用MATALB中Bioinformatics Toolbox进行SVM训练，相关设置主要包括核函数及其参数的选择以及分类面确定方法。高斯径向基核如式(7)所示，

高斯径向基核在诸多工程实际问题中表现优异[19]，故本文选用其作为核函数，并取径向基函数宽度σ=1。最小二乘支持向量机(Least square support vector machines, LS-SVM)是原始SVM的一种改进算法，其可在一定程度上解决SVM的计算复杂性问题，求解速度快[24]，因此本文选用LS-SVM作为分类面确定方法。

4 基于危险点分布比率-SVM的安全域估计方法

训练SVM进行轨道不平顺幅值分类以获取最佳分类面(即其安全域边界)，则需要将各不平顺幅值进行“安全”或“危险”标记。基于预处理后的3个安全性指标，为提高高速运行情况下的安全余量并兼顾乘车舒适度，采用如下评判规则[25]进行轨道激励各点的标记：

其中：C为脱轨系数；RWLRR为轮重减载率；FWRLC为轮轨横向力；LSWL(Static wheel load)为静轮重，本文中SWL=48.690 kN；y为判别变量，y=+1表示“安全”；y=-1表示“危险”。

理论上，标记完成后即可利用标记数据进行SVM分类器训练。但由于存在高低和轨向2种不平顺的最不利相位复合而导致较小的不平顺幅值对安全性指标影响较大的现象[2]，以及脱轨系数和轮重减载率等安全性指标未超限时轨道状态不良，而安全性指标超限但运行状态安全的实际情况[26]，导致标记后的“安全”和“危险”2类数据分布广度相当。而这将使分类器训练难度过大，且会出现SVM为提高其分类正确率将所有输入数据均处理为支持向量，造成过度学习进而导致无法得到最佳分类面的后果。图4所示为速度为320 km/h时标记完成的二维轨道激励数据。可见：利用此数据训练SVM分类器效果不理想。

鉴于此，本文提出基于危险点分布比率(Danger points distribution ratio, DPDR)-SVM轨道不平顺数据分类方法(简记为DPDR-SVM方法)。该方法并非直接对一次标记完成后的轨道不平顺幅值数据进行分类，而是将不平顺幅值区域进行网格划分并基于一次标记数据点计算每网格的DPDR，并根据DPDR阈值对每个网格进行二次标记，再利用SVM对标记完成的网格进行分类以获取不平顺幅值安全域边界。DPDR值为每网格中危险点个数N1与网格中所有采样点个数N的比值，如式(9)所示，其值越大表示此方格代表的不平顺幅值安全性越低(即危险性越高)。二次标记的评判规则如式(10)所示。

其中，bDPDR为DPDR阈值；y′为二次标记的判别变量，y′=+1表示“安全”；y′=-1表示“危险”。

速度为320 km/h时二维不平顺幅值区域的网格划分及各网格危险点分布比率见图5。与图4比较可见：基于DPDR进行不平顺幅值数据分类可大大降低SVM的处理难度，提高算法效率和精度。

图4 一次标记后的二维轨道激励(v=320 km/h)Fig.4 Two dimensional track irregularities after the first mark(v=320 km/h)

图5 二维不平顺幅值区域网格划分及各网格危险点比率(v=320 km/h)Fig.5 Meshing and DPDR of each grid in two dimensional track irregularities (v=320 km/h)

为将以各网格点为代表的幅值数据进行分类，需要依据安全要求高低设置DPDR的阈值，进而对各网格进行标记(即二次标记)，即安全性要求越严格则DPDR阈值应设置的越小，反之越大的DPDR阈值则对应的安全要求越低。在此，为分析危险点个数所占比例分别大于等于50%和等于100%，即网格内至少有一半的点为危险点和所有点都是危险点这2种情况，DPDR阈值则分别取为0.5和1.0。

DPDR-SVM方法的具体实现步骤如下：

Step 1：根据仿真模型输出的3安全性指标的值以及评判标准式(8)，将高低、轨向二维轨道激励数据点区分为安全点和危险点，完成一次标记；

Step 2：确定二维轨道不平顺的幅值区域和网格划分间隔，对该区域进行网格划分；

Step 3：统计每个网格内的危险点个数和采样点个数，按式(9)计算每网格的DPDR值；

Step 4：确定一个DPDR阈值，用于评判各网格所代表的不平顺幅值是否安全；

Step 5：比较各网格的DPDR和DPDR阈值，将各网格区分为“安全”和“危险”2类，完成二次标记；

Step 6：基于标记后的网格，初始化并训练SVM分类器，获取最佳分类面(安全域边界)。

依据现有的轨道不平顺幅值管理标准[7]，本文中轨向和高低不平顺幅值区间均设为[0, 22]mm，横纵坐标的网格划分间隔均为0.5 mm，如图5所示。

5 试验及结果

在分类器训练中，将采集的不同速度下的4组数据(每组1 800对输入输出数据对)按6:4的比例分为训练数据和测试数据2部分。

表1所示为试验过程中不同速度和DPDR阈值下的危险格数目及测试数据的分类正确率。图6所示为基于DPDR-SVM方法的速度为200，240，280和320 km/h时，不同的DPDR阈值所获得的轨道不平顺幅值安全域边界。由式(9)可知，在同一速度下，利用DPDR阈值标记各网格是否安全时，该阈值越大，危险格个数应越少，所获取的安全域边界应距离原点越远。由表1和图6可见，各速度下DPDR阈值为1.0时均比其为0.5时危险格个数少，且其值为1.0的安全域边界基本包含在其值为0.5时的安全域边界内，这符合对DPDR的直观认识。此外由表1可见，由于v=200 km/h，DPDR阈值为1.0时，危险格个数过少而导致分类精度略低，除此之外其余各情况下的测试数据分类正确率均高于0.8，验证了本文提出的DPDR-SVM方法在高速铁路轨道不平顺幅值安全域估计中的有效性和精确性。

图7所示为DPDR阈值为0.5和1.0时，不同速度下的轨道不平顺峰值安全域边界，由图7可见：低速时的安全域边界包围了高速时的安全域边界，即随速度的增大安全域范围变小，进一步验证了本文提出方法的有效性和可行性。因为仿真实验轨道不平顺幅值数据的数据量有限，无法完全覆盖不平顺幅值区域，出现了不平顺幅值安全边界与横纵坐标轴的交点处的值小于安全边界横纵坐标方向的最大值。因此，为提高安全余量，取安全边界在横纵坐标方向的最大值。

图6 基于DPDR-SVM方法的各速度下轨道不平顺峰值安全域边界Fig.6 Boundaries of security regions of track irregularities amplitude at different speeds

图7 基于DPDR-SVM方法的不同DPDR阈值下轨道不平顺峰值安全域边界Fig.7 Boundaries of security regions of track irregularities amplitude at different DPDR thresholds

表1 不同速度及DPDR阈值下的危险格个数和分类正确率Table1 Number of danger girds and classification accuracy under different speeds and different DPDR thresholds

表2所示为不同速度不同DPDR阈值时的轨道不平顺幅值安全域边界所对应的轨向和高低不平顺峰值。由表2可知：速度为320 km/h时，若取DPDR阈值0.5为安全评判规则，则认为高低和轨向不平顺幅值分别不超过9.96 mm和4.95 mm时可保证行车安全；若取DPDR阈值1.0为安全评判规则，则认为高低和轨向不平顺幅值分别不超过12.59 mm和7.76 mm时可保证行车安全。通过与文献[7]中德、美、日等国及我国现有的高速铁路轨道不平顺幅值管理标准相比较，可验证表2中结果的合理性，且有力地说明了文中方法的正确性和可靠性。

表2 不同速度及DPDR阈值下高低和轨向轨道不平顺峰值Table2 Peak amplitude of vertical and lateral irregularities at different speeds and different DPDR thresholds mm

6 结论

(1)针对高速铁路轨道不平顺幅值安全域的边界估计问题，基于数据分类的思想，提出了一种基于危险点分布比例-SVM分类的安全边界估计方法。

(2)基于危险点分布比例-SVM的分类方法可以极大地降低不平顺幅值数据分类的难度，提高分类效率和准确率。

(3)利用基于危险点分布比例-SVM的分类方法获得了高低和轨向二维轨道不平顺峰值的安全域边界，试验结果和与各国现有轨道不平顺幅值管理标准的比较验证了本文提出方法的正确性和可行性。所获取的轨道不平顺幅值安全域边界可以为高速铁路轨道不平顺的标准制定和幅值管理提供参考。

(4)后继研究工作包括加入水平和轨距轨道不平顺激励，以完成更加完备的轨道不平顺峰值安全域估计，以及基于估计出的安全域进行轨道平顺状态的安全评价。由于DPDR阈值对安全域边界估计结果影响较大，因此提出合理的DPDR阈值确定方法也是今后的研究工作之一。

[1]罗林, 张格明, 吴忘青, 等.轮轨系统轨道平顺状态的控制[M].北京: 中国铁道出版社, 2006: 27-62.LUO Lin, ZHANG Ge-ming, WU Wang-qing, et al.Control of track irregularity in wheel-rail system[M].Beijing: China Railway Publishing House, 2006: 27-62.

[2]翟婉明.车辆-轨道耦合动力学[M].3版.北京: 科学出版社,2007: 106-113.ZHAI Wan-ming.Vehicle-track coupling dynamics[M].3rd ed.Beijing: Science Press, 2007: 106-113.

[3]Shafiullah G M, Shawkat A B M, Thompson A, et al.Predicting vertical acceleration of railway wagons using regression algorithms[J].IEEE Transactions on Intelligent Transportation Systems, 2010, 11(2): 290-299.

[4]Gua G, Lilley D M, Franklin F J.A structural articulation method for assessing railway bridges subject to dynamic impact loading from track irregularities[J].Vehicle System Dynamics, 2010, 48(10): 1077-1095.

[5]Atsushi F, Akiyoshi Y.Identification of rolling stock lateral dynamic characteristics and their track irregularity maintenance applications[J].Quarterly Report of RTRI, 2005, 46(1): 7-12.

[6]Hirofumi T, Atsushi F.Management method for large wheel loads and lateral forces using axle-box acceleration and track irregularity[R].Quarterly Report of RTRI, 2009, 50(2): 116-122.

[7]许玉德, 李海锋, 戴月辉.轨道交通工务管理[M].上海: 同济大学出版社, 2007: 24-55.XU Yu-de, LI Hai-feng, DAI Yue-hui.Track maintenance &management for urban mass transit[M].Shanghai: TongJi University Press, 2007: 24-55.

[8]练松良, 黄俊飞.客货共运线路轨道不平顺不利波长的分析研究[J].铁道学报, 2004, 26(2): 111-115.LIAN Song-liang, HUANG Jun-fei.Study of the detrimental wavelengths of track irregularities for railways with passenger and freight traffic[J].Journal of the China Railway Society, 2004,26(2): 111-115.

[9]吴旺青.秦沈客运专线300 km/h综合试验段轨道不平顺管理标准建议值的研究[J].铁道标准设计, 2003(4): 1-4.WU Wang-qing.Research on recommended value of track irregularity management standards in Qinhuangdao-Shenyang dedicated passenger line[J].Railway Standard Design, 2003(4):1-4.

[10]李明华, 李立林, 何晓源.高速铁路轨道不平顺幅值控制研究[J].铁道工程学报, 2009(9): 26-30.LI Ming-hua, LI Li-lin, HE Xiao-yuan.Research on the control of track irregularity of high-speed railway[J].Journal of Railway Engineering Society, 2009(9): 26-30.

[11]Cheli F, Corradi R, Diana G, et al.Effect of track geometrical defects on running safety of tramcar vehicles[J].Vehicle System Dynamics, 2006, 44(Supplement): 302-312.

[12]Alfi S, Bruni S.Estimation of long wavelength track irregularities from on board measurement[C]//The 4th International Conference on Railway Condition Monitoring.Derby: IEEE Press, 2008: 1-6.

[13]陈果, 翟婉明, 左洪福.250 km/h高速铁路轨道不平顺的安全管理[J].西南交通大学学报, 2001, 36(5): 495-499.CHEN Guo, ZHAI Wan-ming, ZUO Hong-fu.Safety management of track irregularities of 250 km/h high-speed railway[J].Journal of Southwest Jiaotong University, 2001,36(5): 495-499.

[14]ZHANG Yuan, QIN Yong, JIA Li-min, et al.Research on methodology of security region estimation of railway system operation safety assessment[C]//Proc of 2011World Congress on Engineering and Technology.Hefei: IEEE Press, 2011: 803-807.

[15]任尊松.车辆动力学基础[M].北京: 中国铁道出版社, 2009:22-56.REN Zun-song.Fundamentals of vehicle dynamics[M].Beijing:China Railway Publishing House, 2009: 22-56.

[16]龙许友, 魏庆朝, 冯雅薇, 等.轨道不平顺激励下直线电机车辆/轨道动力响应[J].交通运输工程学报, 2008, 8(2): 9-13.LONG Xu-you，WEI Qing-chao，FENG Ya-wei, et al.Dynamic response of linear metro vehicle/track excited by track irregularity[J].Journal of Traffic and Transportation Engineering,2008, 8(2): 9-13.

[17]UIC leaflet 518.Testing and approval of railway vehicles from the point of view of their dynamic behavior-Safety-Track fatigue-Ride quality[S].

[18]Vapnik V N.The nature of statistical learning theory[M].New York: Springer-Verlag, 1999: 3-113.

[19]陈然, 孙冬野, 秦大同, 等.发动机支持向量机建模及精度影响因素[J].中南大学学报: 自然科学版, 2010, 41(4):1391-1397.CHEN Ran，SUN Dong-ye，QIN Da-tong, et al.A novel engine identification model based on support vector machine and analysis of precision-influencing factor[J].Journal of Central South University: Science and Technology, 2010, 41(4):1391-1397.

[20]沈超, 蔡忠闽, 管晓宏, 等.基于鼠标行为特征的用户身份认证与监控[J].通信学报, 2010, 31(7): 68-75.SHEN Chao, CAI Zhong-min, GUAN Xiao-hong, et al.Userauthentication and monitoring based on mouse behavioral features[J].Journal on Communications, 2010, 31(7): 68-75.

[21]HU Tan-gao, PAN Yao-zhong, ZHAGN Jin-shui, et al.Integration of soft and hard classifications using linear spectral mixture model and support vector machines[J].Spectroscopy and Spectral Analysis, 2011, 31(2): 508-511.

[22]王宇红, 黄德先, 高东杰, 等.基于支持向量机的非线性预测控制技术[J].信息与控制, 2004, 33(2): 133-136.WANG Yu-hong, HUANG De-xian, GAO Dong-jie, et al.Nonlinear predictive control based on support vector machine[J].Information and Control, 2004, 33(2): 133-136,

[23]车红昆, 吕福在, 项占琴.多特征SVM-DS融合决策的缺陷识别[J].机械工程学报, 2010, 46(16): 101-105.CHE Hong-kun, LU Fu-zai, XIANG Zhan-qin.Defects identification by SVM-DS fusion decision-making with multiple features[J].Journal of Mechanical Engineering, 2010, 46(16):101-105.

[24]桑海峰, 王福利, 何大阔, 等.基于最小二乘支持向量机的发酵过程混合建模[J].仪器仪表学报, 2006, 27(6): 629-633.SANG Hai-feng, WANG Fu-li, HE Da-kuo, et al.Hybrid modeling of fermentation process based on least square support vector machines[J].Chinese Journal of Scientific Instrument,2006, 27(6): 629-633.

[25]中国铁道科学研究院.各类轨道检测方式的系统对比及关联技术研究[R].北京: 中国铁道科学研究院, 2009: 38-43.China Academy of Railway Sciences.Research on systems comparison and associated technologies of various types of track detection methods[R].Beijing: China Academy of Railway Sciences, 2009: 38-43.

[26]曾庆元, 向俊, 周智辉, 等.列车脱轨分析理论及应用[M].长沙: 中南大学出版社, 2006: 38-56.ZENG Qing-yuan, XIANG Jun, ZHOU Zhi-hui, et al.Theory and application of the train derailment analysis[M].Changsha:Central South University Press, 2006: 38-56.