基于软件网络错误传播分析的软件质量量度

2012-08-01 05:39潘伟丰李兵

中南大学学报（自然科学版） 2012年11期

潘伟丰，李兵

(1.浙江工商大学计算机与信息工程学院，浙江杭州，310018；2.武汉大学软件工程国家重点实验室，湖北武汉，430072；3.武汉大学计算机学院，湖北武汉，430072)

复杂网络可以用来描述从技术到生物直至社会各类开放复杂系统的骨架，而且是研究它们拓扑结构和动力学性质的有力工具，已成为极其重要且富有挑战性的科学前沿。近年来，统计物理和复杂系统科学领域的研究人员尝试将软件结构用网络的形式来描述，即将软件元素(方法、类、包等)视为节点，元素之间关系(调用、继承、关联等)作为边的软件网络，并结合复杂网络的最新研究成果，对大量开源软件系统进行了深入研究。如在软件网络拓扑结构特性研究方面，Potanin等[1-3]在不同层次(方法、类和包等)对大量开源软件的依赖网络进行了分析，发现这些网络都具有“小世界”和“无标度”特性；韩明畅等[4-5]对Java和Linux等软件系统进行分析，也发现了类似的结果。在软件网络演化机理研究方面，Krapivsky等[6]提出了一种基于复制和分岔规则的软件演化模型；He等[7]从设计模式的角度提出了基于模式冷冻部分的软件演化生长模型；Pan等[8]根据软件网络中节点和边之间的交互与动态变化，提出了一种基于软件网络的软件演化模型。在软件复杂性度量和评估方面，Vasa等[9]提出了一套度量指标来检测软件开发过程中软件结构的稳定性变化；Ma等[10]提出了一个层次型的度量体系，从不同层次、不同角度度量大规模软件系统的各种结构特性。在软件网络指导工程实践方面，Pan等[11]提出了一种基于复杂网络社区发现的软件重构技术。但是，目前从软件系统复杂网络的角度来研究软件结构，揭示软件内部结构和外部质量间关系的文献较少。MacCormack等[12]提出了传播代价(Propagation cost)的概念，并用于研究文件间的耦合网络，从易变性角度衡量软件的质量。刘婧等[13]定义了平均传播代价(Average Propagation Ratio)，探讨了面向对象软件网络的结构与平均传播代价的内在关系，并用平均传播代价对类级软件网络的质量进行量化。这些方法都是先求得单个节点的影响范围，然后求所有节点影响范围之和，最后将这个和进行单位化，作为系统质量的度量指标。实际上，这些方法考虑的仅仅是单个节点对整个软件网络结构的平均影响范围，即单个节点改变(如修改、出错等)会影响到的其他节点的数量，以此来评估软件的质量。然而，现实中往往是多个节点同时改变，如多个节点同时被修改、出错等，此时，研究这些改变对软件网络结构的影响对衡量软件的质量至关重要。鉴于此，本文作者提出一种用于研究软件质量的新方法，该方法将面向对象软件系统在方法层次抽象成网络模型——方法调用网络，通过随机和受控的方式向网络中植入错误，研究错误在网络中的传播行为，并定义新的度量来刻画错误传播对软件结构造成的影响，以此来量度软件的质量。

1 基本概念及分析方法

图1所示为本文分析方法的基本框架。以OO(Object-Oriented，OO)软件为研究对象，对其源代码进行语法/词法分析，得到方法及方法间的调用关系；提取方法调用网络；基于方法调用网络进行错误植入研究；通过错误植入研究量度软件质量。

1.1 OO软件源代码

本文选择开源的OO软件(主要指以c++和Java开发的系统)作为研究对象，主要出于以下考虑：(1)现有的相关研究工作，主要以OO软件系统为研究对象，采用相同的编程范型，便于结果的比较和分析；(2)OO编程范型从20世纪90年代开始就广为流传，网上具有大量的开源软件系统，便于获取大量实验源数据；(3)采用OO编程技术开发的软件系统，内部结构比较清晰，软件元素(方法、类、包等)及它们之间的关系比较容易提取。

1.2 软件网络模型

目前，使用复杂网络模型研究软件系统主要集中于3个层次，即方法层次、类层次和包层次。本文主要研究方法层次的软件网络的质量。

定义1 方法调用网络MCN(Method-calling network)。面向对象软件系统的方法调用网络MCN可以用1个有向图表示，即N=(M,C)。其中：N为网络MCN；M为节点的集合，代表软件中所有方法的集合；C为有向边的集合，表示方法间的调用关系，由调用者指向被调用者。如图2所示，方法b( )调用方法a( )，则MCN中有1条从b( )指向a( )的有向边。

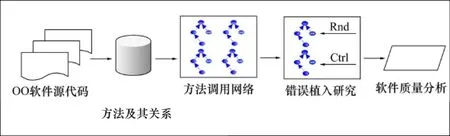
图1 方法基本框架Fig.1 Framework of proposed method

图2给出了1段Java写的源代码及其对应的MCN。

图2 代码段及对应的MCNFig.2 Code segment and its MCN

目前还没有一种开源的工具能够直接从软件源代码提取方法调用网络。本文所有软件的MCN都是由我们自主研发的软件网络分析工具SNAT[14](Software network analysis tool)自动提取的。SNAT可以实现从OO软件源代码生成各个层次(方法、类、包)的软件网络，然后，对软件网络进行一系列的度量、分析、可视化等，但该工具目前还不是开源的。

1.3 错误传播特征及错误植入算法

错误传播是分析可靠性系统不确定性的基本问题，可以发现系统中最易受到毁坏的部分及各部分之间的相互影响[15]。目前已有很多关于错误传播方面的研究，如Voas等[16]提出了软件中的错误传播分析，主要用于计算某一源代码位置传播数据错误的概率；Hiller等[17]提出了一个分析软件中数据错误传播的框架；Johansson等[18]对操作系统内部的错误传播进行了分析，等。但是，本文的错误传播分析方法与以往的不同，是基于软件拓扑结构的。

软件错误种类各异，对系统的破坏性也不尽相同。有些软件错误能够导致系统的崩溃(如内存非法访问)，而大部分的错误一般只是造成系统的输出不能满足用户的要求。本文从软件拓扑结构(方法调用网络)的角度，通过错误植入来对软件的质量进行研究，并不能详尽地表达这些错误种类间的差别。为了简化问题的研究，忽略了不同错误对软件破坏程度的差异，并假设：(1)所有的错误仅仅会对软件的运行正确性造成影响；(2)错误仅仅会在方法调用网络中传播。也就是说，错误只会出现在方法中，这些错误仅仅造成软件不能完成既定的功能，不会给系统带来严重的影响(如崩溃)，某个方法(节点)若存在错误，错误仅仅会传播到与之有直接或间接关系的其他方法(节点)。

为了严格描述错误在MCN中的传播过程，首先给出错误传播关系及其他相关概念的形式化定义。

定义2 错误传播关系(Error propagation relation)EPR(i,j)。设EPR是MCN节点集上的二元关系，i和j表示2个不同的节点。对于任一有序的节点对(i,j)，当且仅当j有1条有向路径通向节点i时，称节点i和节点j存在错误传播关系EPR(i,j)，表示若节点i为错误节点，那么节点i的错误会传播到节点j，使节点j也成为错误节点。

性质1 错误传播关系具有自相关性，即(i,i)∈EPR恒成立。

性质2 错误传播关系具有传递性。如果(i,j)∈

定义3 错误传播域(Error-propagation field)EPF(i)。设EPF是MCN节点集上的一元关系，i和j示节点i的错误传播域。显然，1个节点的错误传播域是该节点存在错误情况下，可能影响的最大范围的一种描述。它由所有与节点i具有错误传播关系的节点特别说明，|*|都表示集合*中元素的个数。

定义4 错误反向传播域(Error back-propagation field)EBPF(i)。设EBPF是MCN节点集上的一元关系，达的所有节点的集合。

定义5 错误介数(Error betweenness)EB(i)。节点i的错误介数定义为其错误反向传播域EBPF(i)中节点的个数，记为EB(i)=|EBPF(i)|。

显然，EBPF(i)描述的是节点i可能受其影响的节点的集合，而EB(i)正是对这种影响能力的度量，即EB(i)越大的节点越容易受其他节点的影响而产生错误。

错误介数与文献[10]中提出的波及度在形式上类似，但两者含义不同。文献主要用波及度对OO软件的结构复杂性进行分析，而本文中的错误介数是对节点出错可能性的一种衡量。

通过深度优先遍历算法，可以在O(|M|+ |C|)时间内得到节点i的EPF(i)，EBPF(i)和EB(i)等值。

为了清楚地说明上面的定义和性质，以1个简单有向网络为例(图3)。这个网络由6个节点和5条有向边组成。若节点D存在错误，因为B存在到节点D的有向路径B→D，F存在到节点D的有向路径所以，D，B，F和E都与D存在错误传播关系，即：EPR(D,D)，EPR(D,B)，EPR(D,F)和EPR(D,E)∈EPR，EPF(D)={D,B,F,E}，|EPF(D)|=4。因为从B出发可达的节点集是{B,D,A}，所以DBPF(B)={B,D,A}，EB(B)=3。

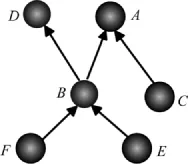
图3 简单的有向网络Fig.3 Simple direct network

软件中的错误通常有2种引入方式：(1)程序员在软件开发中不小心引入的错误，这些错误的引入往往是随机的，其错误的引入位置、时间等都是不确定的；(2)人为地恶意破坏程序中的代码。为了研究软件的质量，模拟软件错误的2种引入方式，进行了软件MCN上的错误植入实验，即：在MCN上选择节点植入错误，根据错误传播关系计算其错误传播域，分析错误植入对软件MCN造成的影响，并以此对软件的质量进行评价。但是，这里考虑的是一种极端的情况，即不断地选择节点植入错误，一直到MCN中所有节点都成为错误节点为止。根据错误植入位置选择方式的不同，分错误随机植入和错误受控植入2种情况来进行研究。

为了衡量错误植入对MCN的影响，首先定义MCN的结构健壮度(Structure robustness)SR。

定义6 结构健壮度SR定义为错误植入后，未受影响的节点数占网络总节点数|M|的比例，即：

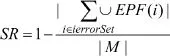
其中：ierrorSet表示MCN中已被选择植入错误的节点集合。以图3为例，若节点B被首先选择植入错误，那么ierrorSet={B}，SR=1-3/6=0.5；若A也被选择植入错误，那么，ierrorSet={A，B}，SR=1-5/6=1/6，以此类推。

从SR的定义可以看出：在相同的错误植入数(即相同的|ierrorSet|)下，SR越大，表明ierrorSet中节点的错误只会传播到较少一部分的节点中去，错误通过软件结构进行传播的能力比较弱，软件结构的容错能力比较强。反之，SR越小，表明ierrorSet中节点的错误对软件造成的影响比较大，错误极易通过MCN传播到其他的部分，并对软件造成极大破坏。因此，可以通过SR来对软件结构的质量进行评价。在相同的错误植入数下，一个结构设计良好的软件应使错误传播控制在尽可能小的范围内(SR尽可能的大)，以降低错误通过软件结构传播对软件造成的影响。

算法1 错误随机植入。错误随机植入，即随机的选择节点植入错误，根据错误传播关系，分析错误在软件MCN中的传播行为，及其对软件(SR)造成的影响。算法步骤如下：

步骤1 提取软件方法调用网络MCN(其实是MCN最大连通子图，见实证部分的说明)作为算法的输入；

步骤2 初始化算法运行的参数，包括：软件MCN的节点数nNodes:=|M|；已经植入的错误数iErrors:=0；MCN中总共的错误节点数nErrors:=0；被选择植入错误的节点集合ierrorSet:=NULL；错误节点集合errorSet:=NULL；

步骤3 若nErrors=nNodes，令fc1:=iError，并保存fc1，转步骤6执行；否则，转步骤4执行；

步骤4 随机的选择节点i(i∈(M-ierrorSet))植入错误，并将其放入集合ierrorSet，即ierrorSet:=ierrorSet∪{i}，计算结构健壮度SR，errorSet:=errorSet∪EPF(i)；iError:=iError+1，nError:=|errorSet|，保存iError和对应的SR；

步骤5 若nErrors＜nNodes，返回步骤3继续执行；否则，执行步骤6；

步骤6 保存数据，结束算法执行。

算法2 错误受控植入。错误受控植入，即按使SR下降最快的节点顺序植入错误。算法如下：

步骤1 提取软件方法调用网络MCN(其实是MCN最大连通子图，见实证部分的说明)作为算法的输入；

步骤3 计算MCN中所有节点i的|EPF(i)|，i∈M。选择具有最大|EPF|的节点im，植入错误，并将其放入集合ierrorSet，即ierrorSet:=ierrorSet∪{im}，并将EPF(im)中的所有节点放入errorSet集，即errorSet:=EPF(im)∪errorSet，并使iError:=iError +1，nError:=|errorSet|，保存iError和对应SR；

步骤4 若nErrors=nNodes，令fc2=iError，并保存fc2，转步骤7执行；否则，转步骤5执行；

步骤6 选择具有最大|EPF|的节点jm，植入错误，并将EPF(jm)中的所有节点放入errorSet集，并使iError:=iError +1，nError:=|errorSet|，保存iError和对应SR，转步骤4继续执行；

步骤7 保存数据，结束算法执行。

比较算法1和算法2可以发现：算法1和算法执行的次数可能不同，但2种算法最终都将使MCN中所有节点都成为错误节点。算法1中，受植入错误节点影响的节点也有可能被选择植入错误；算法2中，一旦某一节点被选择植入错误，则受该节点影响而出错的其他节点将不可能被选择植入错误。

虽然结构健壮度SR可用来描述错误动态植入过程中软件结构的变化，但是，仍缺乏相应的度量来对软件整体的结构质量进行衡量。基于错误植入实验中保存的SR值，提出了一个新的度量指标——软件质量系数(Software quality coefficient)SQC，用于从整体上对软件的质量进行评估。

从SQC的定义可以看出：它综合考虑了软件错误随机植入和受控植入对软件造成的影响，能够比较全面的从错误传播的角度对软件的质量进行度量。用SQC评价软件质量，SQC值越大说明软件结构的质量越好，错误通过软件结构进行传播的能力比较弱，软件结构具有好的容错能力；SQC越小，说明软件结构对软件错误比较敏感，软件错误比较容易通过软件的拓扑结构“放大”，从而对软件造成极大破坏。因此，结构设计良好的软件应使SQC尽可能大，以降低错误引入对软件造成的影响。

2 实例验证

2.1 数据来源

对将近20个开源的面向对象系统进行实例研究，都发现了类似的结果。这里以其中4个有代表性的系统为例进行说明。这些系统包括Tomcat 6.0.18(用java编写的免费的Web服务器，支持Servlet和JSP规范，源代码可在http://to mcat.apache.org/下载)、Azureus(用java编写的BitTorrent的客户端应用程序，用于下载发布的网上资源，源代码可在http://azureus.sourceforge.net/下载)、Jxtaim0.1i(用java编写的基于java加密扩展JCE和JXTA的即时通讯系统，源代码可在http://jxtaim.sourceforge.net/下载)和jfreechart1.0.12(用java编写的开放的图表绘制类库，是为application，applets，servlets以及JSP等使用所设计的。源代码可在http://www.jfree.org/jfreechart/下载)。软件规模(即方法的个数)从1万多到3万多不等。结果如表1所示。

从软件源代码提取的MCN，并非是全连通的，往往有几个子图构成。由于一个子图上的错误不会传播到另外一个子图，所以本文只关注各软件MCN的最大弱连通子图MWCC[19](Maximal Weekly Connected Components)，以此来对软件的结构质量进行研究。实验中，算法1和算法2的输入为MCN的最大弱连通子图MWCC。图4所示为各软件MCN最大弱连通子图的网络图。

表1 实验系统的规模Table1 Statistics of subjects

图4 软件MCN的网络图Fig.4 Networks for MCNs of software

本文的实验策略如下：首先，用MCN模型来描述这4个软件系统，提取各个系统的MCN；然后，采用错误植入方法研究错误随机植入和错误受控植入对MCN结构健壮度SR的影响，并分析决定SR的一些关键因素；最后，计算软件质量系数SQC，从整体上评价软件的质量，同时引入随机有向网络模型分析不同因素对软件质量系数SQC的影响。

2.2 实验结果与分析

图5(a)～(d)所示为4个软件MCN的结构健壮度SR与植入错误节点比例P(即|ierrorSet|/总的节点数)的关系曲线图。为了降低随机因素对实验结果的影响，每个错误随机植入实验都独立运行了10 000次，计算每次运行中的SR，然后取平均值。

从图5(a)～(d)可以发现：(1)在错误随机植入和错误受控植入时，随着P从0增加到1，4个系统MCN的SR都从1迅速下降，这说明软件系统是非常脆弱的，软件错误极易通过软件的拓扑结构进行传播，造成软件大部分功能的失效；(2)错误受控植入时，SR的下降速度都比在错误随机植入时要快。这说明软件MCN对随机错误具有一定的容错能力，但是，对错误受控植入侧很脆弱，少量节点的出错就会使整个系统的性能降低一半；(3)在错误随机植入和错误受控植入的过程中，一旦P超过某一临界值(错误随机植入时的Pc1，错误受控植入时的Pc2)，SR都减为0，出现了一种类似于“反向渗流转变”的现象[20]。这说明，一旦P超过某一临界值，错误就传播到了MCN的所有节点中。并且错误受控植入时的临界值Pc2一般比错误随机植入时的Pc1要低得多。这是因为在错误受控植入是按SR下降最快的节点顺序植入错误的。

由于MCN的SR值是通过|EPF|来计算的，因此，可以推测上述这些特征可能与节点的|EPF|有关。为此，研究了上述4个系统的|EPF|及其与其他参数的相互关系。

图5(e)～(h)所示为4个系统相应的累积|EPF|分布。可见：这些系统的累积|EPF|分布大致服从幂率分布，而且具有“长尾”特征。这说明，网络中大多数的节点只有很小的|EPF|，而少数节点却拥有很大的|EPF|。所以，在错误随机植入时，拥有较小|EPF|的节点更有可能先被选择植入错误，而错误受控植入是按SR下降最快的顺序选择节点植入错误的，因此，错误选择性植入时，SR的下降速度比在错误随机植入时更快。

同时，研究了节点|EPF|和EB的相互关系，其散

点图如图6所示。图中每个节点代表1个方法(|EPF|，EB)对。可以发现：虽然这些系统来自不同的领域，但|EPF|和EB的相关性都展现了相似的趋势，即：|EPF|大的节点一般拥有较小的EB，而EB大的节点一般|EPF|较小。这说明那些EB大的节点(处于较高层次的方法)若植入错误，对系统其他部分的影响比较小，而|EPF|大的节点(处于较低层次)对系统的影响比较大，若它们被植入错误，将导致其他很多部分也出错。在错误随机实验过程中发现，导致错误随机植入时SR快速下降的不是那些具有较大|EPF|的节点(如图6中矩形框内的点)，因为这些节点数量较少，而是图6中直线以上的节点，这些节点为数众多，而且EB比较大，极易受其错误反向传播域中节点的影响而成为错误节点。而那些同时具有较大|EPF|和EB的节点(如图中椭圆框内的节点)是最易出错且危害也比较大的节点。因为这些节点拥有较大的EB，极易受到其错误反向传播域中节点的影响而成为错误节点，一旦这些节点出错，它又将影响其EPF中的节点，导致错误快速的在MCN上传播，使SR迅速下降。

图5 SR vs.P和Pcum(|EPF|)vs.|EPF|图Fig.5 SR vs.P and Pcum(|EPF|)vs.|EPF|

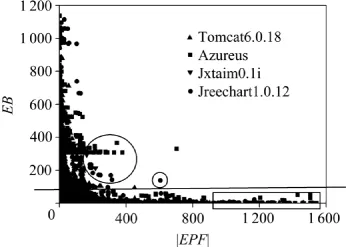
图6 各系统|EPF|和EB的散点图Fig.6 Scatter point graph of |EPF| and EB

各个节点|EPF|与其入度和出度的pearson线性相关性分析结果如表2所示，其中，Kin和Kout分别表示节点的入度和出度。从表2可以发现：节点的|EPF|和其入度之间具有显著度为0.01的正相关性。这说明入度大(重用率高)的节点，它们的|EPF|(影响范围)往往很大，一旦这些入度大的节点出错，将给系统带来比较大的危害。这一点与文献[10]中的研究结果相符。所以，重用虽然提高了软件开发的效率，但是，也可能给软件质量带来威胁，一旦重用率高的方法出错，将造成其他很多方法也出错。因此，对重用率高的方法，应该加大测试的力度，确保其正确性。同时还发现|EPF|与其出度具有显著度为0.01负相关性，这说明处于较低层次的方法(|EPF|大的节点)不倾向于调用其他的方法。

表2 |EPF|和出/入度的相关性分析Table2 Correlation analysis of |EPF| and in/out-degree

为了从总体上评价错误植入对软件造成的影响，从而评价软件结构的质量，计算了各个系统的SQC，结果如表3所示。通过对比表1和表3可以发现：SQC大的系统，其规模不一定小(如Azureus的SQC在4个系统中排第2，但其规模在4个系统中是最大的)，反之亦然。这表明并不是规模越大的系统就越难以保障其质量，越简单的系统其质量就越容易控制，软件的质量与软件的规模间并没有必然的因果关系。

表3 MCN的SQC值Table3 SQC of MCN

由于网络的结构可以通过各种参数来进行描述，如结构熵、平均度等[10]。为了进一步研究SQC和这些网络统计参数之间的关系，引入文献[21]中的随机有向网络模型，用该模型生成具有相同规模(即节点数)、不同边数的有向网络，并研究了网络结构熵、平均度、平均|EFP|(各节点|EFP|之和取平均值)、平均EB(各节点EB值之和取平均值)与SQC之间的相互关系。生成的网络节点数为1 000，边数从3 000到10 000不等。每种边数的网络都生成100个实例，计算得到的网络的结构熵、平均度、平均|EFP|、平均EB和SQC，然后取平均值，以降低随机因素的影响。图7所示为具有相同节点数，不同边数的网络的结构熵、平均度、平均|EFP|、平均EB和SQC。其中：H表示网络的结构熵；avg(Degree)表示平均度；avg(|EPF|)表示平均|EFP|；avg(EB)表示平均EB。表4所示为部分参数间的pearson线性相关性分析。

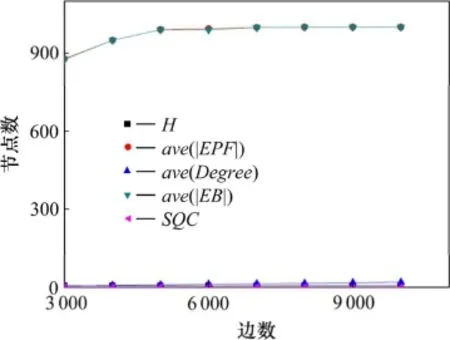
图7 Tomcat 6.0.18有向网络Fig.7 Direct networks of Tomcat 6.0.18

表4 参数间线性相关性分析Table4 Correlation analysis of parameters

从图7和表4可以发现：(1)在网络规模一定的情况下，随着网络中边数的增加，结构熵H、平均度avg(Degree)，avg(|EPF|)和avg(EB)也随之增大，但是，SQC逐渐减小。这说明在网络规模一定的情况下，边数的增加使网络越来越“无序”，网络的连通性增强，avg|EPF|和avg(EB)增大，软件质量系数SQC下降，即软件的结构比较便于错误在其上传播。因此，在软件开发中，要将方法间的交互关系数控制在一定的范围内；(2)网络结构熵H和平均|EPF|之间存在着显著度为**的强正相关性，与SQC间存在显著度为**的负相关性。这说明在网络规模一定的情况下，网络越“无序”，其平均错误传播域就越高，软件质量就越低，极易被破坏。因此，软件开发应该使软件保持一定的“有序”性，这有利于提高软件的质量。这与文献[10]中的研究结果相符；(3)avg|EPF|与软件质量系数SQC存在显著度为**的负相关性。这说明网络的平均错误传播域越大，软件质量就越低。

3 结论

(1)将复杂软件系统抽象成方法调用网络，研究了错误在该网络上的传播行为，提出了量度软件质量的新度量——软件质量系数(SQC)。

(2)SQC能有效度量软件质量，并与其他结构参数具有密切的联系：①节点|EPF|的幂律分布且具有“长尾”特征使软件结构在错误随机植入时比错误受控植入时更加健壮；②错误介数大的节点的大量存在使得软件系统比较脆弱，极易被破坏；③入度大(重用率高)的节点是系统的关键点，这些点的出错将给系统造成极大的损坏；④软件质量系数与网络中的边数有关，在网络规模一定的情况下，边数的增大将降低软件质量系数；⑤软件质量系数与软件的结构熵有关，在网络规模一定的情况下，软件的结构熵越大(“无序”)，软件质量系数就越低；⑥软件质量系数与软件的平均错误传播域有关，在网络规模一定的情况下，平均错误传播域越大，软件质量系数就越低。

[1]Potanin A, Noble J, Frean M, et al.Scale-free geometry in OO programs[J].Communications of the ACM, 2005, 48(5):99-103.

[2]Concas G, Marchesi M, Pinna S, et al.Power-laws in a large object-oriented software systems[J].IEEE Transactions on Software Engineering, 2007, 33(10): 687-708.

[3]Pan W F, Li B, Ma Y T, et al.Multi-granularity evolution analysis of software using complex network theory[J].Journal of Systems Science and Complexity, 2011, 24(6): 1068-1082.

[4]韩明畅, 李德毅, 刘常昱, 等.软件中的网络化特征及其对软件质量的贡献[J].计算机工程与应用, 2006, 42(20): 29-31.HAN Ming-chang, LI De-yi, LIU Chang-yu, et al.Networked characteristics in software and its contribution to software quality[J].Computer Engineering and Application, 2006, 42(20):29-31.

[5]闫栋, 祁国宁.大规模软件系统的无标度特性与演化模型[J].物理学报, 2006, 55(8): 3799-3084.YAN Dong, QI Guo-ning.The scale-free feature and evolving model of large-scale software systems[J].Acta Phsica Sinica,2006, 55(8): 3799-3084.

[6]Krapivsky P L, Redner S.Network growth by copying[J].Physical Review E, 2005, 71(3): 036118.

[7]He K Q, Peng R, Liu J, et al.Design methodology of networked software evolution growth based on software patterns[J].Journalof Systems Science and Complexity, 2006, 19(2): 157-181.

[8]Pan W F, Li B, Ma Y T, et al.A novel software evolution model based on software networks[C]//1st International Conference of Complex Networks.Shanghai, 2009: 1281-1291.

[9]Vasa R, Schneider J G, Nierstrasz O.The inevitable stability of software change[C]//23nd IEEE International Conference on Software Maintenance.Paris, 2007: 4-13.

[10]Ma Y T, He K Q, Du D H, et al.A complexity metrics set for large-scale object-oriented software systems[C]//6th IEEE International Conference on Computer and Information Technology.Seoul, 2006: 189-194.

[11]Pan W F, Li B, Ma Y T, et al.Class structure refactoring of object-oriented software using community detection in dependency networks[J].Frontier of Computer Science in China,2009, 3(3): 396-404.

[12]MacCormack A, Rusnak J, Bald Win C Y.Exploring the structure of complex software designs: An Empirical Study of Open Source and Proprietary code[J].Manag Sci, 2006, 52:1015-1030.

[13]Liu J, Lu J H, He K Q, et al.Characterizing the structural quality of general complex software networks[J].International Journal of Bifurcation and Chaos, 2008, 18(4): 605-613.

[14]刘婧.基于复杂网络的软件结构分析及优化研究[D].武汉:武汉大学软件工程国家重点实验室, 2007L 10-32.LIU Jing.Research on software structure analysis and optimization by applying complex network methodology[D].Wuhan: Wuhan University.State Key Laboratory of Software Engineering, 2007: 10-32.

[15]李爱国, 洪炳镕, 王司.基于错误传播分析的软件脆弱点识别方法研究[J].计算机学报, 2007, 30(11): 1910-1921.LI Ai-guo, HONG Bing-rong, WANG Si.An approach for identifying software vulnerabilities based on error propagation analysis[J].Chinese Journal of Computers, 2007, 30(11):1910-1921.

[16]Voas J, Morell L J.Propagation and infection analysis (PIA)applied to debugging [C]//IEEE Southeastcon’90.New Orleans,LA, 1990: 379-383.

[17]Hiller M, Jhumka A, Suri N.EPIC: Profiling the propagation and effect of data errors in software[J].IEEE Transactions on Computers, 2004, 53(5): 512-530.

[18]Johansson A, Suri N.Error propagation profiling of operating systems[C]//2005 International Conference on Dependable Systems and Networks (DSN).Yokohama, 2005: 86-95.

[19]Myers C R.Software systems as complex networks: Structure,function, and evolvability of software collaboration graphs[J].Physical Review E, 2003, 68(4): 046116.

[20]Albert R, Jeong H, Barabasi A L.Error and attack tolerance of complex networks[J].Nature, 2000, 406(6794): 378-382.

[21]Batagelj V, Mrvar A.Pajek 1.24[EB/OL].[2012-10-11].http://pajek.imfm.si/doku.php?id=down load