CCM Buck变换器的精确反馈线性化滑模变结构控制*

乐江源 谢运祥 冀玉丕 张志

(1．华南理工大学电力学院，广东广州510640;2．赣南师范学院物理与电子信息学院，江西赣州341000)

以微分几何为基础的非线性控制理论近20年来得到了迅速发展，其中提出的状态反馈精确线性化的非线性控制设计方法引起了大量研究者的关注．该方法的核心思想是通过适当的非线性状态和坐标变换，使非线性系统实现状态或输入/输出的精确线性化，从而将复杂的非线性综合问题转化为线性系统的综合问题．它与传统的利用泰勒展开式进行局部线性化近似方法不同，在线性化过程中没有忽略掉任何高阶非线性项，因此这种线性化不仅是精确的，而且是整体的，即线性化对变换有定义的整个区域都适用［1-4］．该方法已经被成功地用于解决一些实际控制问题［5-10］．文献［7-10］中将该方法应用于DC/DC开关变换器的控制，取得了明显优于PI控制的效果，这也为该方法在更复杂电力电子系统中的应用提供了可能．

就目前研究现状来看，基于微分几何理论的反馈线性化非线性控制方法在电力电子中的应用是建立在非线性系统的精确数学模型假设的基础上的，未考虑实际系统的不确定性，因此鲁棒性不强，在实际系统应用中有很大的局限性．而滑模变结构控制以其对系统参数摄动以及外界干扰特有的强鲁棒性深受重视，近20多年来在非线性领域也取得了突破性的进展［4］．由于电力电子变换器固有的开关特性，滑模变结构控制在各类电力电子变换器中也得到了广泛应用［11-20］．但目前的滑模变结构控制设计大多采用控制变量与参考量的误差为切换函数，无法对滑动模态的动态品质进行优化控制．理论上说，考虑系统的非线性特性，选取的切换函数也应该是非线性的．

基于以上原因，文中以CCM Buck变换器为研究对象，尝试将精确反馈线性化与滑模变结构控制相结合，提出了Buck变换器精确反馈线性化滑模变结构控制策略．该方法结合了精确反馈线性化非线性控制与滑模变结构控制的优点，一方面可以利用滑动模态对于不确定性与干扰的不变性，减弱精确反馈线性化方法对精确数学模型的依赖性，提高整个控制系统的鲁棒性;另一方面精确反馈线性化有助于建立线性滑模函数，线性滑动模态可以利用线性理论改善其动态性能．文中还利用仿真工具，将该方法与无源性滑模变结构控制方法相比较，验证了该方法的动态响应特性和强鲁棒性．

1CCM Buck变换器仿射非线性系统模型

CCM Buck变换器工作原理如图1所示．

图1 Buck变换器原理图Fig．1 Working principle of Buck converter

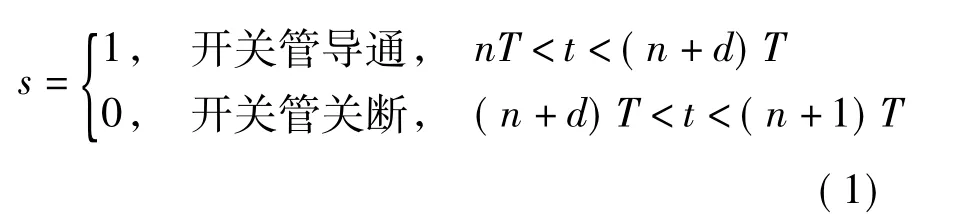
DC-DC变换器是一种典型的双线性动态系统，其工作状态随开关管的通断在不同模态间切换．可定义以下开关函数s:式中，T为开关周期，d为占空比函数;n、n+1分别表示第n、n+1个开关周期．状态变量可根据储能元件的个数确定，选取电感电流iL和输出电容电压uo为状态变量，利用开关函数可建立如下状态方程:

开关频率足够高时，采用状态空间平均法，可将状态空间平均模型表示为

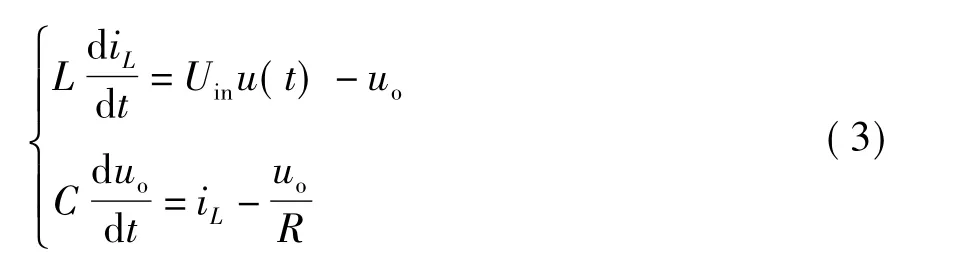
式中，u(t)为占空比随时间变化的函数．令x1=iL，x2=uo，由于实际系统中的Uin是输入电压量，不具有可控性，因此不能作为系统的控制变量．只能选取占空比函数u(t)作为控制变量，且令u(t)=u．因此可得到单输入单输出仿射非线性系统的标准形式如下:

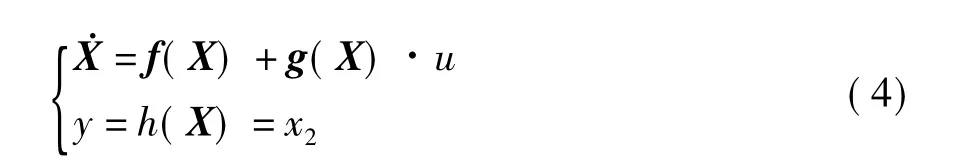
2CCM Buck变换器状态反馈精确线性化

经过上述变换，得到了适合微分几何方法的仿射非线性模型，该模型的特点是:对于状态变量可能是非线性的，对于控制变量则是线性的．下面在上述模型的基础上，应用微分几何方法对非线性系统进行反馈精确线性化．首先验证是否满足精确反馈线性化条件，为此计算李括号Lfg(X):

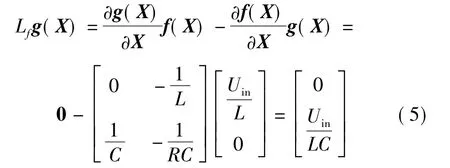
再考察系统给定的原输出函数能否直接作为坐标变换进行线性化，为此计算原输出函数对应的关系度:

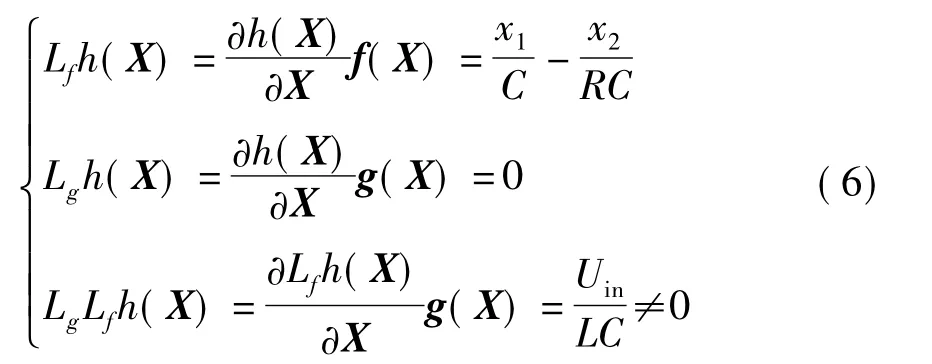
由式(6)可知，状态方程(4)定义的输出函数对应的系统相对阶为2，等于系统的维数．因此可得到坐标变换为

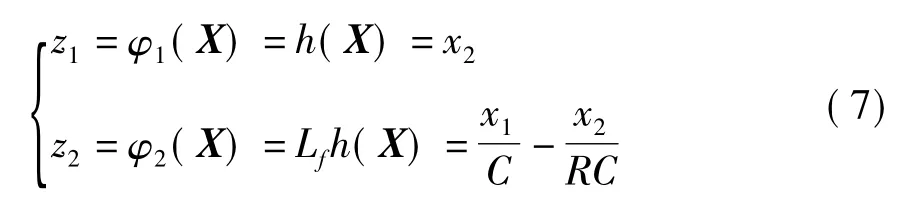
在坐标变换Z=Φ(X)条件下，原非线性系统可变换成线性系统布鲁洛夫斯基标准型:

式中:Z为变换后线性系统的状态变量，Z=(z1，z2);v为新的控制变量，它与原非线性系统控制变量u有如下关系:

为此计算式(9)中的李导数L2fh(X)和LgLfh(X):

3 基于状态反馈精确线性化的滑模变结构控制器设计

经过上述精确反馈线性化后，原非线性系统转化成了能控线性系统．由于微分同胚的映射关系，可以在线性系统上设计控制器实现非线性系统的控制功能．考察Buck变换器的控制目标是使输出电压uo跟踪参考电压uoref．当系统达到稳态时，可计算出电感电流iL参考值iLref为

根据坐标变换关系式(7)，可得到线性系统(8)的状态变量的参考值为

式中，z1ref、z2ref分别表示坐标转换后的线性系统的状态变量z1和z2的参考值．至此，原非线性系统的控制问题转化为线性系统的跟踪控制问题．为了进一步将跟踪问题转化成系统在原点(0，0)的镇定问题，定义以下误差变量:

将其代入式(8)可得到以误差变量E为状态变量的状态方程:

则可得到滑动模态运动方程:

可取线性切换函数为

因此只要保证c1＞0，即可保证滑动模态在原点(0，0)上渐进稳定，调节c1的取值，可调节滑动模态的动态品质．

利用坐标反变换，可得原非线性系统的切换流形s(X)及相应的等效控制ueq(X):

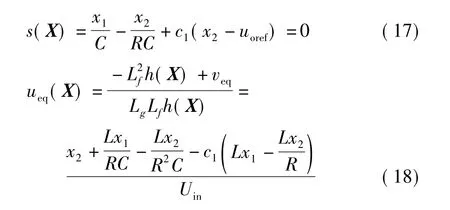
由此可知，系统由某一初始状态经过趋近运动到达切换流形，然后在等效控制下沿切换流形向平衡点滑动．但由于实际控制量u是受限的，并不是切换流形上的每个点都能引起滑模运动．根据实际控制量的取值范围可确定滑动模态区为

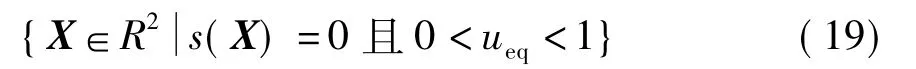
下面求取变结构控制u±(X)，使到达条件得到满足．依据滑模变结构控制的一般规律，系统能够在有限的时间内到达切换流形，但滑模变结构控制固有的抖振现象将使电力电子变换器表现为开关纹波较大．一般而言，根据特定的趋近律来设计变结构控制是一种既可保持变结构的鲁棒性又能减小抖振的方法．下面采用指数趋近律进行u±(X)的设计．令

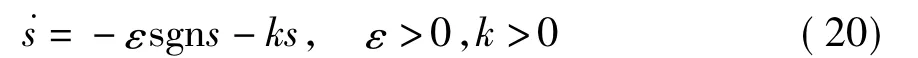
可得

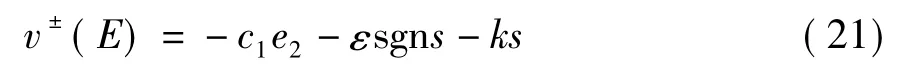
转换成x1、x2坐标空间的变结构控制为

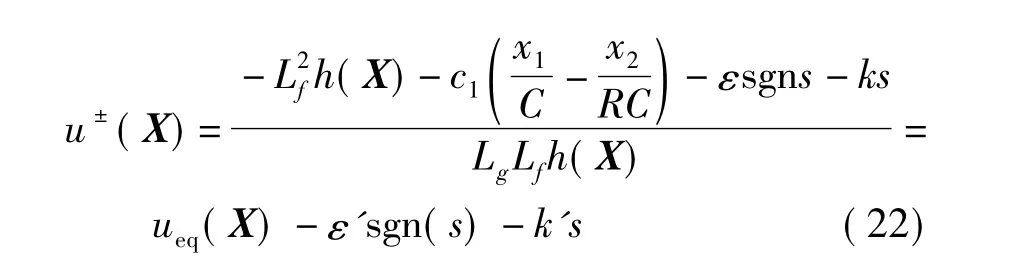
4 数值仿真及实验

为了验证所提出的控制策略的性能，采用Matlab仿真软件对基于状态反馈精确线性化滑模变结构控制的系统进行数值仿真，仿真系统电路结构如图1所示．仿真系统基本参数为:输入电压Uin=12V，输出电压Uoref=5V，负载电阻R=5Ω，开关频率fs=100kHz，输入电感L=1mH，输出滤波电容C=100μF．

为了说明所提出的新型控制策略具有良好的动静态性能，分别在启动过程、负载电阻周期性扰动和输入电压周期扰动3种情形下，与文献［18］中所提出的无源性控制策略进行了对比分析．为保证对比的有效性，无源性控制策略的注入阻尼R1在较大范围内进行了优化设置，分别研究了注入阻尼R1取0．01、0．10和 1．00 Ω 时的系统启动过程．基于状态反馈精确线性化滑模变结构控制策略的控制参数选取为:c1=1000，ε =5 ×105，k=8 ×104．

4．1 启动响应特性对比

图2给出了系统在两种不同控制策略下的启动特性曲线．其中图2(a)、图2(b)和图2(c)分别为注入阻尼 R1取 0．01、0．10 和 1．00 Ω 时无源性控制策略下的启动特性曲线，图2(d)为基于状态反馈精确线性化滑模变结构控制策略的启动特性曲线．由图可知:无源性控制策略在不同注入阻尼的情况下，启动过程中电感电流和输出电压都存在超调现象和振荡过程，随着注入阻尼的增大，超调有所减小，但振荡过程加长，增加了系统达到稳态的过渡时间．而基于状态反馈精确线性化滑模变结构控制策略的系统启动过程，跟无源性控制策略比较，具有无超调、无振荡过渡过程的特点，系统很快达到稳态，响应时间短，说明新型非线性复合控制策略具有更优越的动态响应特性．另外，从系统达到稳态后的波形对比分析也可看出:新型非线性复合控制策略的电感电流和输出电压的波动小，纹波少，说明其具有更优越的稳态特性．

图2 两种控制方法的电感电流和输出电压启动波形Fig．2 Starting waveforms of inductor current and output voltage when using two controllers

4．2 负载突变时的动态响应特性对比

图3为负载电阻由5．0Ω跳变到2．5 Ω时两种控制策略的动态响应曲线，其中图3(a)为新型非线性复合控制策略在负载电阻突变时电感电流和输出电压的动态响应曲线．由图可看出:电感电流在负载电阻突变时能迅速响应，并稳定在新的稳态值，且无超调、无振荡过渡过程;而输出电压在负载电阻突变的瞬间存在一定的超调(约0．5 V左右)，但能很快恢复到设定的参考电压，无振荡过渡过程．图3(b)为无源性控制策略在负载电阻突变时电感电流和输出电压的动态响应曲线．由图3可看出:电感电流在负载电阻突变时存在较大的超调，并伴随着约一个周期的振荡过渡过程;而输出电压在负载电阻突变的瞬间也存在较大的超调(约2 V左右)，同样存在一个周期的振荡过渡过程．对比分析可知:在负载扰动的情况下，新型非线性复合控制策略比无源性控制策略具有更好的动态响应特性，响应速度快，超调量小，说明采用新型非线性复合控制策略的系统具有更强的鲁棒性及带负载能力．

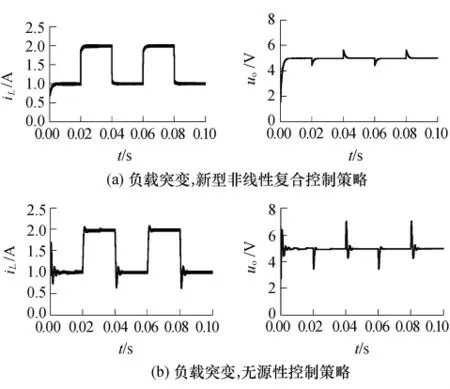
图3 两种控制方法在负载扰动下的输出电压和电感电流动态响应波形Fig．3 Dynamic response waveforms of output voltage and inductor current when using two controllers with load disturbance

4．3 输入电压动态响应特性对比

图4为输入电压由12 V跳变到18 V时两种控制策略的动态响应曲线．其中图4(a)为新型非线性复合控制策略在输入电压突变时电感电流和输出电压的动态响应曲线，由图可看出:电感电流和输出电压基本上不受输入电压扰动的影响．图4(b)为无源性控制策略在输入电压突变时电感电流和输出电压的动态响应曲线，由图可看出:电感电流和输出电压在输入电压突变瞬间都存在超调和振荡，并存在一定的稳态静差．对比分析可知:新型非线性复合控制策略对输入电压的扰动表现出非常强的鲁棒性，这点可以从控制律(22)得到理论解释，因为控制律的分母为输入电压Uin，当输入电压存在扰动时，直接调节占空比，可迅速维持输出电压的稳定．因此，采用新型非线性复合控制策略的系统具有更宽的输入电压适用范围．

图4 两种控制方法在输入电压扰动下的输出电压和电感电流动态响应波形Fig．4 Dynamic response waveforms of output voltage and inductor current when using two controllers with input voltage disturbance

4．4 实验验证

为了验证所提出的新型非线性控制方法的正确性，基于TMS320F2812设计了控制系统，进行了实验研究．相关电路参数及控制系统参数与仿真时一致．

图5为系统稳态时的输出电压和电感电流波形．由图5可知:电感电流按照开关频率周期性波动，输出电压波形稳定，纹波小，与理论分析和仿真波形一致．输出电压与设定值有一定的静态误差，分析可知是由于输入电感的电阻及MOS管的导通压降造成的．

图6为周期性投切附加负载时，输出电压和电感电流的动态响应波形．从波形可以看出:输出电压在负载突变时，有较小的超调，但很快过渡到电压稳定值;而电感电流迅速调节到新的稳定值，无振荡，无超调．说明所提出的控制方法同样具有良好的动态性能．

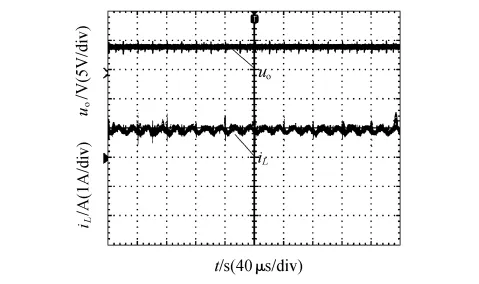
图5 新型非线性控制方法下输出电压和电感电流的稳态响应波形Fig．5 Steady-state response waveforms of output voltage and inductor current with novel nonlinear control method

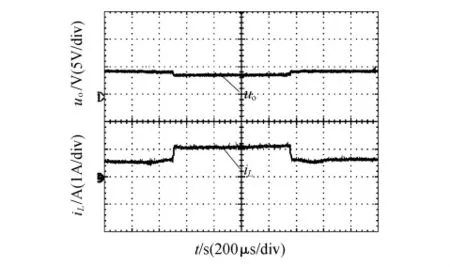
图6 负载扰动下输出电压和电感电流的动态响应波形Fig．6 Dynamic response waveforms of output voltage and inductor current with load disturbance

5 结语

文中提出了一种基于精确反馈线性化的Buck变换器滑模变结构控制方法，先通过精确反馈线性化方法将原非线性系统映射成简单的线性系统，实现了原非线性系统的解耦控制，再采用线性切换函数和指数趋近律设计了滑模变结构控制器．仿真比较及实验验证表明，文中所提出的控制方法具有以下优点:

(1)由于采用了精确反馈线性化，实现了原非线性系统的解耦控制，因此系统的动态响应速度提高，稳态精度得到改善．

(2)由于结合了滑模变结构控制技术，因此所设计的控制系统具有强鲁棒性，减弱了精确反馈线性化控制方法对系统数学模型的强依赖性，为精确反馈线性化先进控制方法的工程应用提供了理论途径．

［1］ Isidori A．Nonlinear control systems［M］．Germany:Springer Verlag，1995:70-87．

［2］ 胡跃明．非线性控制系统理论与应用［M］．北京:国防工业出版社，2005:68-100．

［3］ 卢强，孙元章．电力系统非线性控制［M］．北京:科学出版社，1993:1-264．

［4］ 高为炳．变结构控制的理论及设计方法［M］．北京:科学出版社，1996:251-275．

［5］ Divelbiss A W，Wen J T．A path space approach to nonholomic motion planning in the presence of obstacles［J］．Robot＆ Automat，1997，13(3):443-451．

［6］ 邓卫华，张波，丘东元，等．三相电压型PWM整流器状态反馈精确线性化解耦控制研究［J］．中国电机工程学报，2005，25(7):97-103．

Deng Wei-hua，Zhang Bo，Qiu Dong-yuan，et al．Research of decoupled control law using state variable feedback linearization method of three-phase voltage source PWM rectifier［J］．Proceedings of the CSEE，2005，25(7):97-103．

［7］ 邓卫华，张波，胡宗波，等．CCM Buck变换器的状态反馈精确线性化的非线性解耦控制研究［J］．中国电机工程学报，2004，24(5):120-125．Deng Wei-hua，Zhang Bo，Hu Zong-bo，et al．Research of nonlinear decoupled control law using state variable feedback linearization method based on the CCM Buck converter［J］．Proceedings of the CSEE，2004，24(5):120-125．

［8］ 邓卫华，张波，丘东元，等．CCM Boost变换器状态反馈精确线性化与非线性PID控制研究［J］．中国电机工程学报，2004，24(8):45-50．

Deng Wei-hua，Zhang Bo，Qiu Dong-yuan，et al．The research of state variable feedback linearization method on the CCM Boost converter and nonlinear PID control law［J］．Proceedings of the CSEE，2004，24(8):45-50．

［9］ 帅定新，谢运祥，王晓刚．基于状态反馈精确线性化Buck变换器的最优控制［J］．中国电机工程学报，2008，28(33):1-5．Shuai Ding-xin，Xie Yun-xiang，Wang Xiao-gang．Optimal control of Buck converter by state feedback linearization［J］．Proceedings of the CSEE，2008，28(33):1-5．

［10］ 高朝晖，林辉，张晓斌．Boost变换器带恒功率负载状态反馈精确线性化与最优跟踪控制技术研究［J］．中国电机工程学报，2007，27(13):70-75．Gao Zhao-hui，Lin Hui，Zhang Xiao-bin．Exact linearization and optimal tracking control of Boost converter with constant power loads［J］．Proceedings of the CSEE，2007，27(13):70-75．

［11］ 周卫平，吴正国，刘大明，等．有源电力滤波器变趋近律滑模变结构控制［J］．中国电机工程学报，2005，25(23):91-94．Zhou Wei-ping，Wu Zheng-guo，Liu Da-ming，et al．The variable reaching law sliding mode control strategy for three-phase three-wire active power filter［J］．Proceeding of the CSEE，2005，25(23):91-94．

［12］ 汤赐，罗安，周柯，等．新型注入式混合有源滤波器的滑模变结构控制［J］．中国电机工程学报，2007，27(19):99-103．Tang Ci，Luo An，Zhou Ke，et al．Sliding mode control of new injection type hybrid active filter［J］．Proceedings of the CSEE，2007，27(19):99-103．

［13］ 郭伟峰，武健，徐殿国，等．新型滑模控制的并联混合有源电力滤波器［J］．中国电机工程学报，2009，29(27):29-35．Guo Wei-feng，Wu Jian，Xu Dian-guo，et al．Hybrid shunt active power filter based on novel sliding mode control［J］．Proceeding of the CSEE，2009，29(27):29-35．

［14］ 倪雨，许建平．准滑模控制开关DC-DC变换器分析［J］．中国电机工程学报，2008，28(21):1-6．Ni Yu，Xu Jian-ping．Quasi-sliding-mode switching control for DC-DC converters［J］．Proceeding of the CSEE，2008，28(21):1-6．

［15］ Sira-Ramirez H，Perez-Moreno R A，Ortega R，et al．Passivity-based controllers for the stabilization of DC-DC power converters ［J］．Automatica，1997，33(4):499-513．

［16］ Malesani L，Spiazzi R G，Tenti P．Performance optimization of cuk converters by sliding-mode control［J］．IEEE Trans on Power Electronics，1995，10(3):302-309．

［17］ Naim R，Weiss G，Ben-Yaakov S．H∞control applied to boost power converters［J］．IEEE Trans on Power Electronics，1997，12(4):667-683．

［18］ 乔树通，伍小杰，姜建国．基于无源性的滑模控制在DC-DC变换器中的应用［J］．电工技术学报，2003，18(4):41-45．Qiao Shu-tong，Wu Xiao-jie，Jiang Jian-guo．Application of passivity-based sliding mode control in DC/DC converters［J］．Trans China Electrotechnical Society，2003，18(4):41-45．

［19］ Guo Xiu-hong，Feng Quan-yuan．Passivity-based controller design for PWM DC/DC Buck current regulator［C］∥Proceedings of the World Congress on Engineering and Computer Science 2008．USA:IEEE，2008:875-878．

［20］ Sira-Ramirez H，Rios-Bolivar M．Sliding mode control of dc-dc power converters via extend linearization［J］．IEEE Trans on Circuit and Systems，1994，41(10):652-661．