移动Mesh网络定位系统研究

王 辉，熊 飞，谷源涛

(1.空军装备研究院通信所，北京100085;2.清华大学电子工程系，北京100084)

0 引言

近年来，无论是在军用还是民用领域，对移动目标定位的应用需求日益强烈。移动位置服务业务已成为最具增长潜力的增值业务之一［1］。当前，移动定位系统研究重点在于定位信息的获取和处理以及提高定位精度和准确度等方面。移动Mesh技术适合于区域环境覆盖和宽带高速无线接入。结合移动Mesh网络宽带高、频谱利用率高的优势，以及具有网络自组织、自维护等特点［2］，提出了一种基于移动Mesh网络的定位系统，在对移动Mesh网络及TDOA(Time dispersion of arrival)定位算法分析的基础上，给出了在3 km×2 km无线覆盖区域中移动Mesh网络“锚”节点(含有卫星定位模块，具有自定位功能的移动Mesh节点)配置方案，利用Mesh节点作为“锚”节点，建立相对坐标系，移动终端通过测量与“锚”节点之间距离，并通过TDOA定位算法获得自身相对位置信息，最后对系统定位性能进行了仿真分析。

1 移动Mesh网络定位技术及定位原理

移动定位是利用移动通信网络，通过对接收信号特征测量分析并计算，为移动终端用户提供相关的位置信息服务［3］。

移动Mesh网络(无线网状网络)也称为“多跳(multi-hop)”网络，它是一种与传统无线网络完全不同的新型无线网络技术，是真正无中心的网络。相对其他无线定位系统，移动Mesh通信网络实现定位有其显著的优势，第一，各Mesh节点均可自由移动，网络拓扑结构具有随机性，又因为Mesh网络无中心节点，因此其抗毁性是其他无线网络所不能比拟的;第二，采用纯IP网络技术，移动Mesh网络拓扑结构可以无限扩展，支持任意数量的节点随意接入;第三，Mesh采用同步网络技术体制，利用系统同步机制，可以方便地得到移动终端与Mesh节点之间的定时同步(信号延时)，进而计算得到它们之间的距离，使其具有了自组织定位能力的先天优势;第四，Mesh支持移动(Point to MutiPoint)模式，为终端拓展提供了便利条件;第五，Mesh支持MAC层设计，具有QOS性能，安全性更高。

移动Mesh网络定位原理与步骤如下:① 建立区域内无线通信网络。建立无线通信网络，满足所有Mesh节点与移动终端之间的网络传输要求;②实现网络内各单元的定位。以无线通信网络为基础，采用一定的定位方法实现各无线通信单元的定位。

无线通信网络主要考虑因素有:

①建立无线局域网(WLAN)，能够满足一定区域内所有节点之间的互联互通;②保证每个移动终端最少与3个以上Mesh节点互联互通以实现定位计算。

采用符合IEEE 802.16e协议的移动Mesh通信网络体制，信道编码采用OFDM技术，选用5 GHz通信频段，最大物理层传输速率20 Mbps，通信距离2～5 km，采用 QPSK/QAM自适应调制，TDD双工模式。

实现系统定位主要考虑因素有:

(1)利用OFDM符号定时同步实现测距

OFDM系统中，发送端信号经过IFFT，接收端要正确解调就必须确定FFT窗口的准确位置，这就产生了所谓OFDM系统符号同步问题［4］。确定FFT的窗口位置，关键是定时估计要准确，即在接收端，通过定时估计得到的时延估计值推算出OFDM符号的起始位置，并将FFT窗口位置调整到此位置。经过调整后，FFT窗口就能够包含OFDM符号上当前帧的全部样值点，最后实现正确的解调。如果对OFDM系统的定时估计不准确，位置没有定位在OFDM帧结构的第1个样值点上，就会引起符号间干扰，造成通信误码或中断。由上可见，OFDM符号同步的关键是定时估计。

这里采用了一种对称共扼序列作为训练序列的定时估计算法，序列结构示意图如图1所示。其中，A部分的序列是由Nu/4(Nu≤N)长的PN序列经过N/4点的IDFT产生，B*部分由A的共扼对称序列产生。

图1 训练序列结构示意图

利用A和B的对称性，定时测度表达式为:

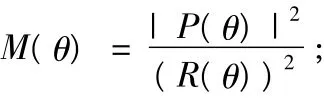
其中:

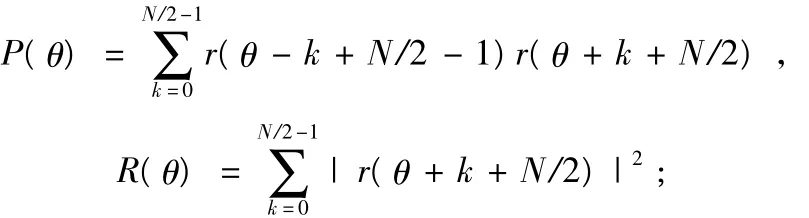
在接收端，将M(θ)取得最大值所对应的采样位置取为定时估计的位置，即定时估计值为:

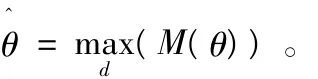
在此算法中，由于R(θ)取值为始终正，从而对P(θ)进行了归一化，但同时也使运算量会增加一倍。由于P(θ+1)和P(θ)的数据不同，由序列的共扼对称性可知P(θ)只有在准确点时出现一个峰值，因此得到的定时估计的精度较高。

OFDM系统中，信号时延τ为收到信号起始时刻tr加上信号偏差θT，再减去信号发送时刻ts:

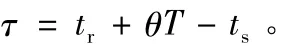
通过对N个OFDM符号进行定时估计可以得到N个测距值，取其平均值，从而得到更为准确的估计值。一般情况下，N取值可为4n，比如256、1 024等，N值越大估计值越精确，但同时运算量也成几何倍数增加。

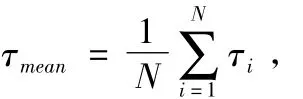
利用信号时延与距离的关系，很容易得到基站与终端之间距离为:

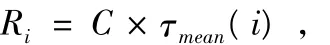
式中，c代表光速，Ri指终端与第i个“锚”节点之间距离，τ(i)指终端与第i个锚节点信号时延。

(2)通过计算得到定位结果

测距算法采用TDOA，定位算法采用最大似然估计算法［5，6］。

最大似然估计算法是常用的定位算法。它对三边定位算法进行了改进，通过增加已知节点数量，利用冗余信息加权定位限制，使定位精度得到很大程度上的提高。所以最大似然估计算法也称作多边定位算法。

最大似然估计算法中，已知n个基站坐标分别为 B1(x1，y1)，B2(x2，y2)，……，Bn(xn，yn)，与移动终端 M(x，y)测得的距离分别为 d1，d2，……，dn，如图2所示。

类似三边定位算法，可以由已知条件建立方程组如下:

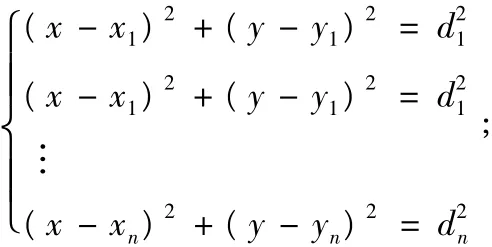
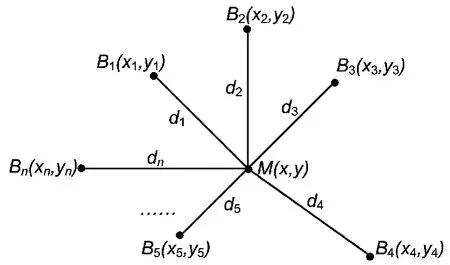
图2 最大似然估计定位算法示意图

采用最大似然估计法(Maximum Likelihood Estimation，MLE)求解方程组，由上面方程中上式依次减去最后一项式可得:

则利用最小均方差估计可以得到M坐标为:

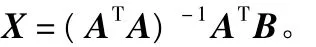
此算法可以很大程度上克服由于测距误差带来的定位误差，定位精度会得到显著提高。

2 仿真分析

2.1 移动Mesh通信网络架构与仿真

根据需要，假定实际应用中要求在某个指定区域，比如3 km×2 km范围中，实际中，必须考虑设备体积与重量，因此，假设设计Mesh基站覆盖半径一定，那么通过计算机仿真，当Mesh节点随机布置到该区域中，取基站覆盖半径分别为1 km，2 km，则基站数量和平均覆盖率(可通信率)关系如图3所示。

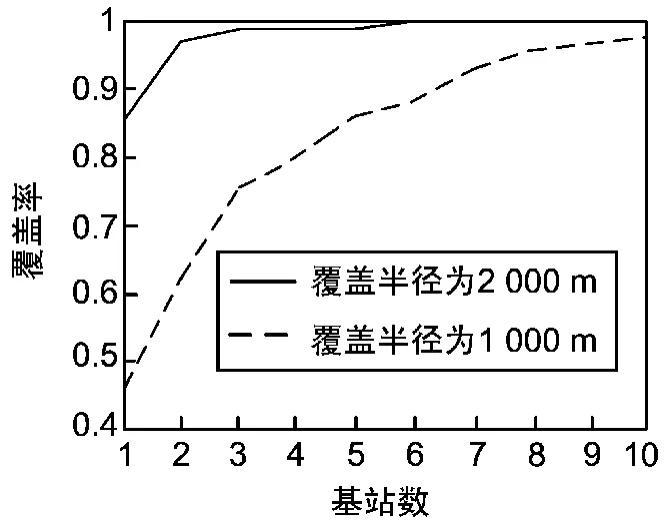
图3 基站数量与覆盖率关系图

仿真结果表明，当移动Mesh节点无线覆盖半径为2 km，随机接入的基站数目达到3个以上时，系统的可接通率达到99%(即系统可信度达到99%)，可满足区域内一般通信网络需求。

2.2 移动Mesh网络定位架构与仿真分析

首先假设Mesh节点自身位置信息已经确定，作为“锚”节点，Mesh节点向终端发送定位信息。可以想象，由于本系统是一个随机拓扑结构的无线网络，Mesh节点的布局将直接影响终端能否实现定位功能。如果系统中移动终端同时必须接收到3个以上Mesh“锚”节点定位信号，就可以认为终端可以实现自身定位。假如在一种情况下，Mesh“锚”节点随机布置到3 km×2 km的区域范围中，节点覆盖半径为2 km，利用计算机进行仿真，则实现定位目的的节点数量与可实现定位的概率之间的关系如图4所示。

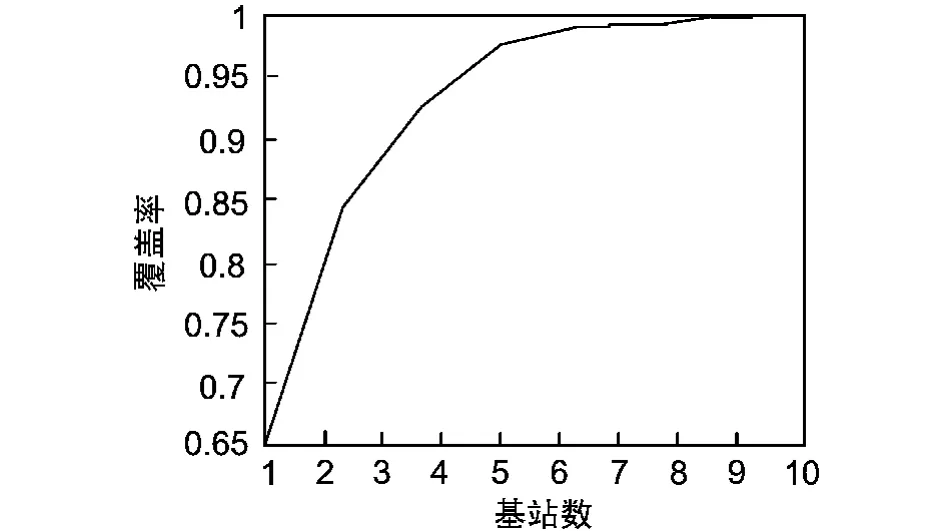
图4 “锚”节点数量与定位概率之间的关系

仿真结果表明，在当前确定网络架构内，当取基站节点数目为6个以上时，此网络基本具备定位能力。

2.3 测距仿真分析

利用OFDM系统定时计算单个Mesh节点与移动节点之间的距离。定时估计采用EC算法，在高斯信道下进行仿真，仿真中采用子载波数取2 048，循环前缀取64，QPSK 调制，符号取224 μs，单个样值点0.109 4 μs，SNR 取0～20 dB，对于每个 SNR 分别仿真1 000次求其平均值。信道采用四径多径衰落信道，时延分别设为 0，10，20，40，信号衰减分别为0，10，20，25 dB。得到 θ与信噪比(SNR)及测距误差关系如图5和图6所示。

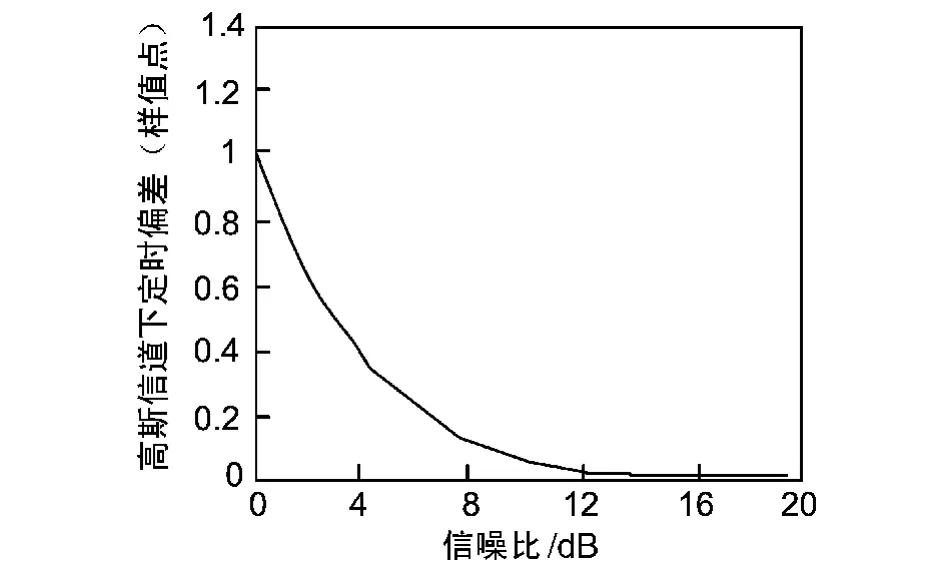
图5 高斯信道下定时偏差与信噪比之间的关系

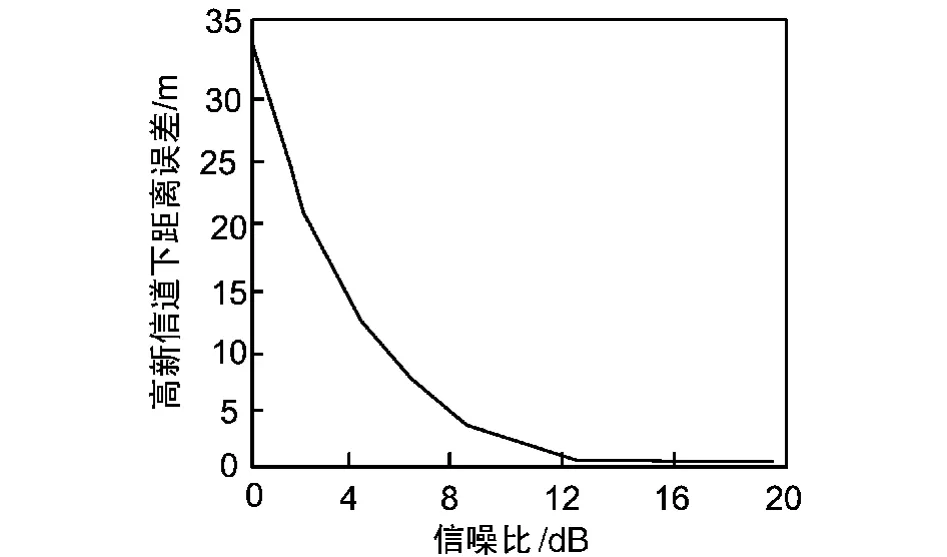
图6 高斯信道下距离误差与信噪比之间的关系

2.4 定位算法仿真及误差分析

该文采用最大似然估计算法，主要对定位精度进行了仿真验证，其初始参数包括随机Mesh节点(“锚”节点)位置、随机移动终端位置，设测距误差分布服从N～(μ，σ)的正态分布，其中 μ等于0，σ值由测距仿真计算得到。仿真结果如图7和图8所示。

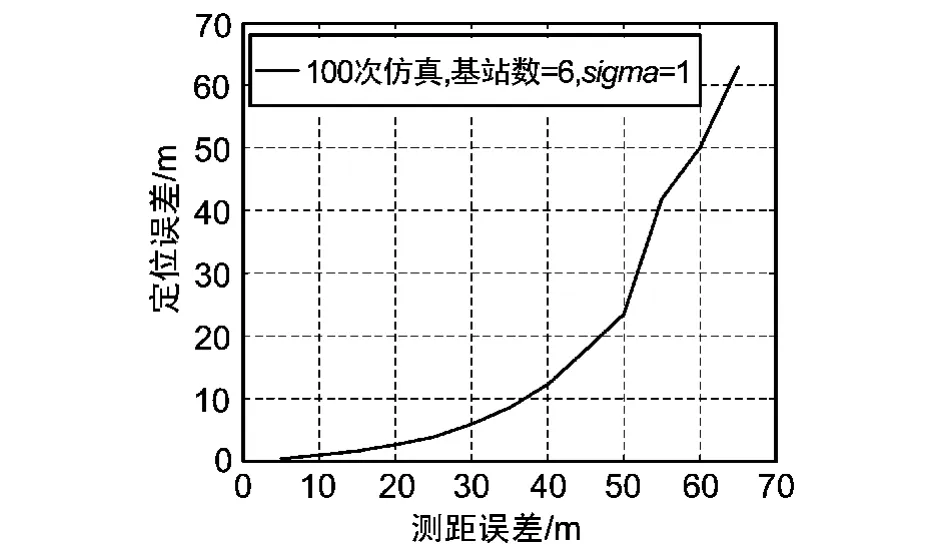
图7 节点服从正态分布(σ=1)情况下定位误差分析

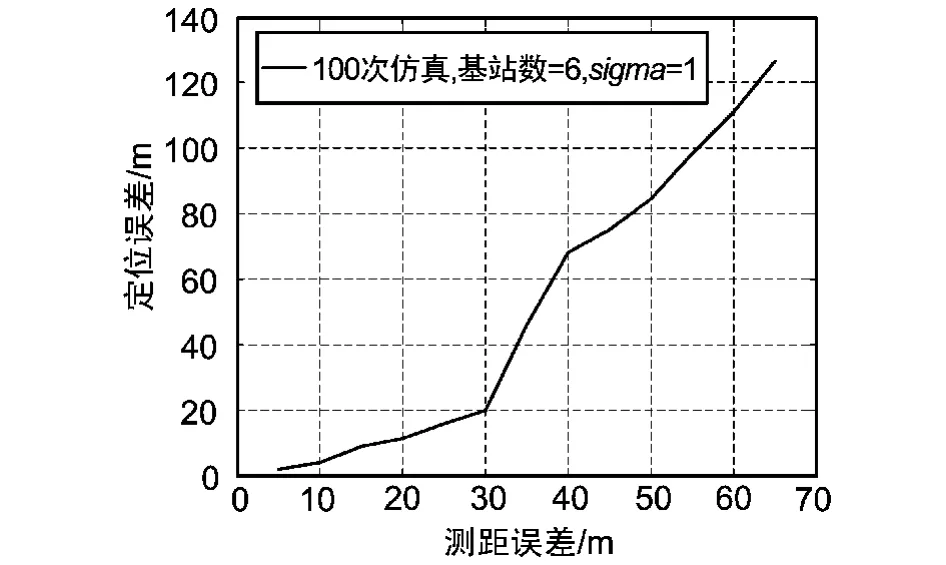
图8 节点服从正态分布(σ=5)情况下定位误差分析

综合考虑网络规划、测距误差以及信道状况等，这里所描述的Mesh定位系统定位误差主要包含2部分，第1个是测距误差，实际仿真结果表明在信噪比比较大，即信道质量较好的情形下，误差范围在米级，对系统定位影响不大;第2个是定位算法带来的计算误差，这里选择的最大似然估计算法，当“锚”节点数量足够多时，定位精度将显著提高，误差精度能够达到米级。

3 结束语

研究了Mesh节点在一定区域内随机布局，Mesh节点位置(坐标)已知情形下该区域中随机移动终端的定位问题。分析了基于OFDM技术下的移动Mesh通信网络中各单元的相对定位问题。对Mesh系统实现定位的关键技术及算法进行了阐述及仿真验证，并综合考虑了随机Mesh网络建立、测距算法及实现和定位算法及实现，分析了基于OFDM模式下Mesh网络实现自定位的可能性与误差分析。

通过仿真验证结论，找到了一种实现移动Mesh网络自定位的方法，其定位精度与定位能力满足一般地面通信系统定位使用的要求。

［1］赛迪顾问通信产业研究中心.2009－2010年中国位置服务(GPS/LBS)市场竞争分析［R］.北京：赛迪集团，2010：1.

［2］宋文，方旭明.无线网状网研究与发展［J］.铁道学报，2007，29(2)：96 －103.

［3］刘瑾.基于测距的无线传感器网络的定位算法的研究［J］.航空计算技术，2009(6)：124 －126.

［4］杨国庆.基于OFDM信号的无源定位技术研究［D］.西南交通大学硕士论文，2008.

［5］WU Hao-yun，LU I-tai.A simple and Accurate Linear Solver for Hyperbolic Localization ［C］∥ IEEE Communications Socie-ty/WCNC 2005：1733 －1736.

［6］杨天池.一种基于TOA定位的CHAN改进算法［J］.电子学报，2009(4)：819 －822.