MIMO-OFDM系统中最大化速率的自适应算法

杨爱敏，张 梅

(北京劳动保障职业学院，北京100029)

0 引言

超3代系统中采用多输入多输出天线(MIMO)和正交频分复用(OFDM)技术能够显著地提高系统的频谱效率。在发射端和接收端采用多天线MIMO系统能有效地增加无线信道的系统容量［1］。OFDM技术最大的特点能够将频率选择性信道转化为多个平坦的子信道。MIMO-OFDM系统结合了MIMO技术和OFDM技术的优点，其高频谱效率吸引了广泛的关注［2－3］。

自适应调制编码技术(AMC)是一种根据已知的信道信息自适应地调整传输参数，由于其自适应性，在下一代移动通信系统中也将被广泛应用［4］。

当信道状态信息(CSI)在发射端和接收端已知的情况下，贪婪算法是最优的算法，然而，由于其高计算复杂度一般应用在理论分析中，而很少应用在实际中。文献［5］中提出了一种在MIMO系统中最大化传输速率的低复杂度自适应调制算法。

1 系统模型

假设MIMO-OFDM系统中有nt根发射天线和nr根接收天线，且 nr≥ nt，其中 N=min{nr，nt}。OFDM系统中有K个正交平行子载波，假设系统中的保护间隔足够长，因此可以认为系统不存在符号间干扰，假设系统不存在载波间干扰因素，即认为系统不存在符号间干扰(ISI)和载波间干扰(ICI)。

系统中发射信号和接收信号之间的关系可以表示为:

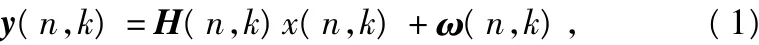
式中，Η(n，k)表示在第n时刻、第k个子载波的信道状态矩阵，它是一个nr×nt的矩阵，x(n，k)表示发射端的发射信号，ω(n，k)表示信道的噪声矩阵，其中此矩阵中的元素服从均值为0、方差为σ2的加性高斯分布。

假设信道在发射端和接收端能够精确获得CSI，MIMO信道可以利用SVD分解得到几个等效的平行子信道，即:

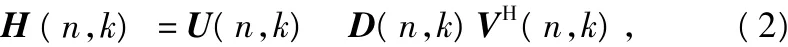
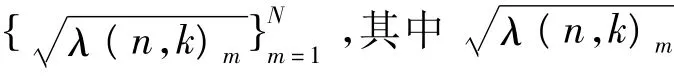
在MIMO-OFDM系统中使用自适应调制算法的系统框图如图1所示。

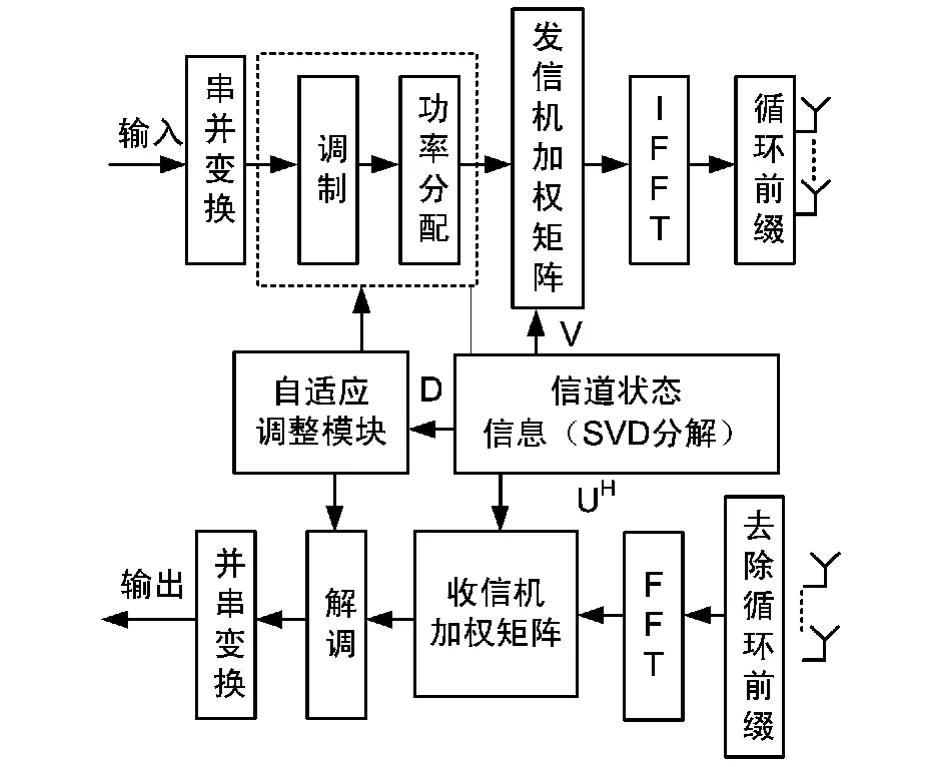
图1 自适应MIMO-OFDM系统框图

2 理论与算法分析

2.1 理论基础

在系统中，可以选择不同的调制模式，记作{M1，M2…Mm}。此算法的目标即在系统的误比特率和发射功率有一定限制的情况下，最大化信息传输速率，因为系统在任一时刻的发射功率限制是一个常数，为了简便，在下面分析中把时刻的标志去除，则此目标可以用数学公式表示为:

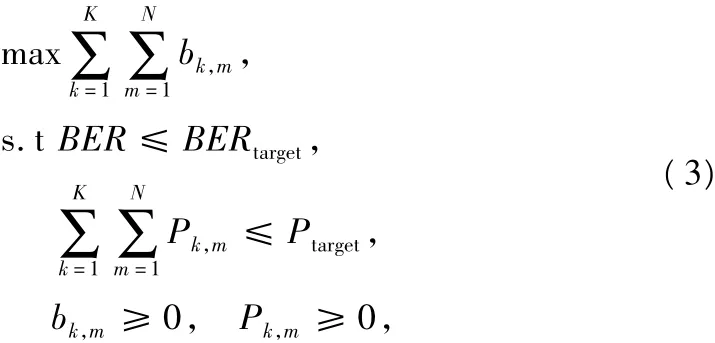
式中，BERtarget和BER是系统对于误比特率的限制值即系统所能忍受的最大的误比特率和系统实际的误比特率，其中Ptarget表示系统的功率限制值，Pk，m和bk，m分别表示第k个子载波上第m个平行子信道所需的功率以及传输的比特数。

在实际系统中，系统的误比特率是比较不容易计算，故而，几乎所有的研究者都是以瞬时BER来代替系统的平均BER。为了简便起见，在下面的推论中，也以瞬时BER代替系统的BER。如果系统中任一时刻任一平行子信道的瞬时误比特率都小于目标BER，这样实际系统中的误比特率就一定会满足系统误比特率要求。

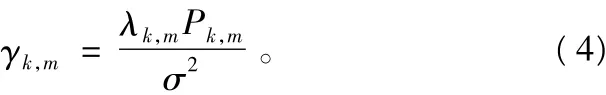
对于方形QAM调制，在文献［6］中提出了关于其BER近似公式，它可以表示为下面的指数形式:

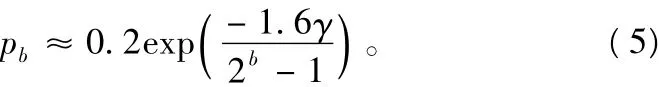
根据式(5)可以得到，如果第k个子载波上第m个平行子信道上分配的比特和功率分别为bk，m和Pk，m，则为了满足系统误比特率要求，其关系可表示为:

如果可选调制模式只有方形QAM，若信道状态极差时bk，m=0表示此对应信道不发送数据信息。由于在此系统中可选的调制模式为方形QAM，则式(3)可以另写为:

将式(6)代入式(8)，式(8)转化为:

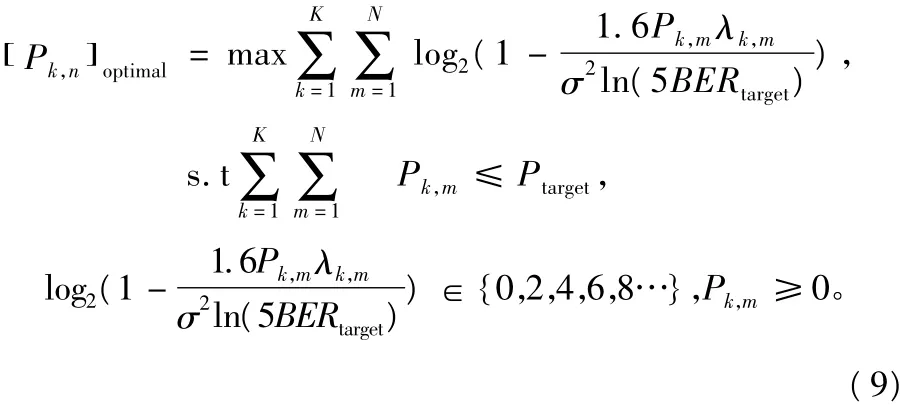
下面为了方便，首先不考虑

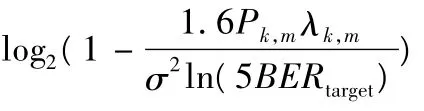
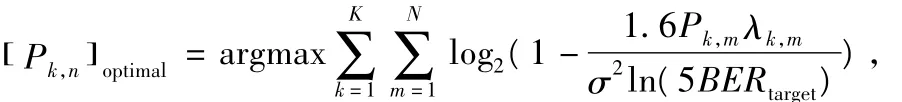
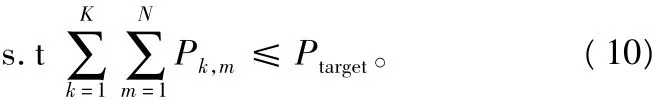
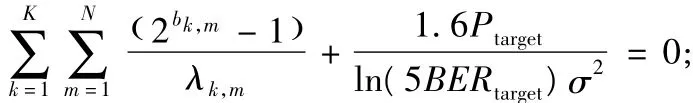
下面利用拉格朗日方法解决式(10)中的最优化问题，其构造的函数为:

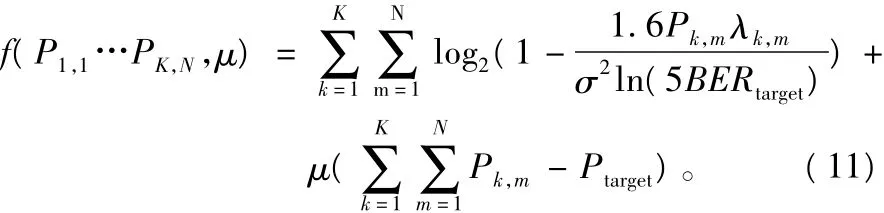
对于第k个子载波上第m个平行子信道上的功率值Pk，m可以通过求解下式得到:

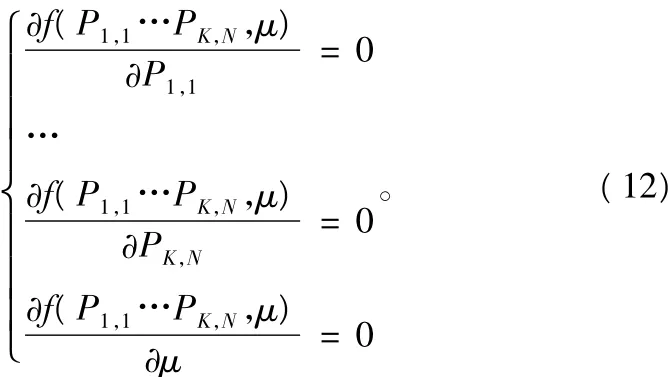
通过求解式(12)，可得:

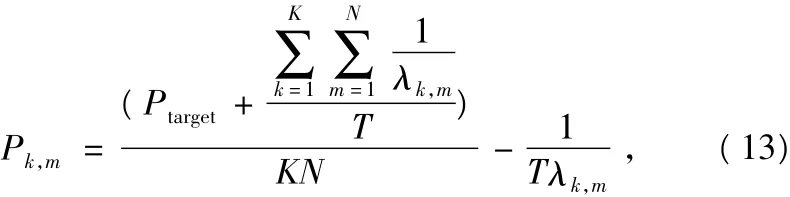
其中:

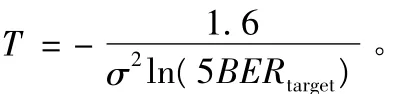
在没有 bk，m∈ {0，2，4，6，8…} 的限制条件下，通过式(13)得到的功率值 Pk，m，如果 Pk，m＜ 0 ，则对应 bk，m=0 ，否则用式(7)求解比特值 bk，m，即为最优化结果，下面讨论如何比特调整使系统满足bk，m∈{0，2，4，6，8…} 。文中提出 2 种调整方案，分别如下。

2.2 调整方案一

①根据首次比特分配结果，对于 bk，m＞0，1≤k≤K，1≤m≤N对应的子信道为激活子信道，设激活子信道数为Non，如果Non=KN，则到步骤③，否则到步骤②;

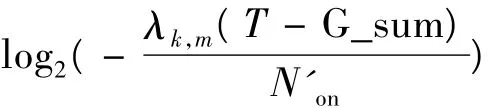
③把所有非激活子信道的比特数赋值为0，激活子信道的比特数调整至距其最近的调制模式对应的比特数，并记作Bk，m，并根据式(6)，计算此信道对应的功率值;

④如果各激活子信道的信息传输功率之和等于目标系统功率限制值，则停止，否则进行如下调整:

第1步:计算各激活子信道上取整后的比特数与根据公式计算的比特数之差，即:

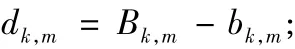
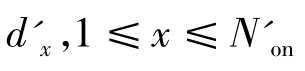
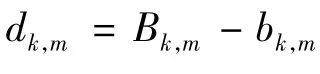
第2步:将dk，m以升序排列，排列顺序后记为，从开始向后，，并计算对 应 的 Pk，n和，如果，则到下一个，直到。对于最后一个做 Bk，m=Bk，m+2 运算的，其对应的 Bk，m和Pk，m，恢复原值。

2.3 调整方案二

①根据首次比特分配结果，如果 bk，m≤ 0，1 ≤ k≤ K，1≤m ≤ N ，令 bk，m=0，对于 bk，m＞ 0，1≤k≤K，1≤m≤N对应的信道为激活子信道，激活子信道数记为Non;

②对于激活子信道的比特数调整为距其最近的调制模式对应的比特数，结果存为Bk，m，对于非激活信道比特数设为Bk，m=0。根据式(6)求解对应的功率值 Pk，m;

③如果各激活子信道的信息传输功率之和等于目标系统功率限制值，则停止，否则进行如下调整:

第1步:计算各激活子信道上取整后的比特数与根据公式计算的比特数之差，即:dk，m=Bk，m－ bk，m;

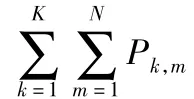
第1步:计算各激活子信道上取整后的比特数与根据公式计算的比特数之差即:dk，m=Bk，m－ bk，m;

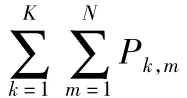
3 仿真结果比较

假设MIMO-OFDM系统中有2根发射天线，2根接收天线，并且OFDM中存在64个正交子载波，信道噪声服从复高斯分布，其均值为0，方差σ2=10－3。在此仿真过程中，假设信道服从均值为0，方差为1的复高斯分布。图2给出在BERtarget一定，BERtarget=10－3的情况下，信息的传输速率随着给定的功率值变化的关系图。图3给出了在给定功率一定，Ptarget=0.5的情况下，信息传输速率随着目标误比特率改变的关系图。

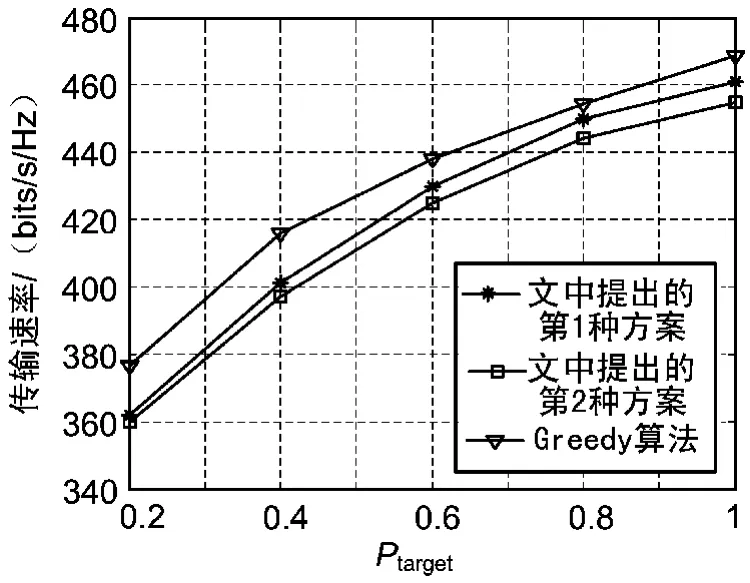
图2 传输速率与功率的关系图

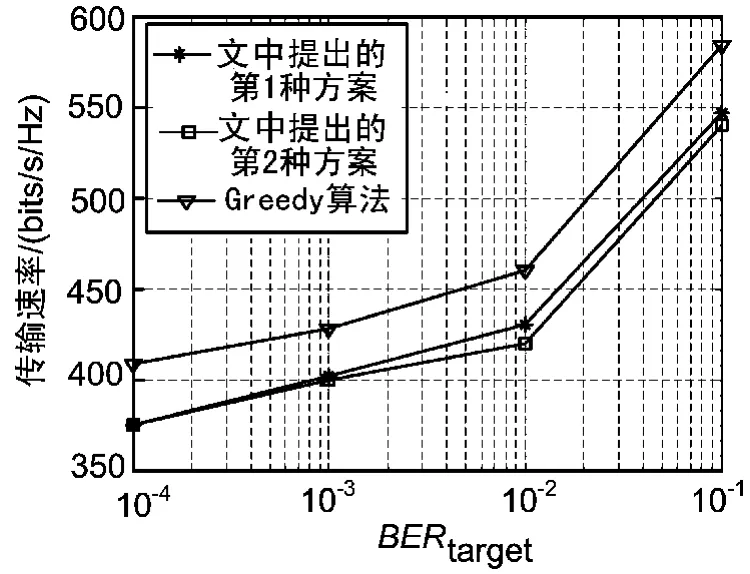
图3 传输速率与BERtarget关系图

从上面2图可以看出，Greedy性能最好，文中提出的第2种方案相对较差，但提出的新算法和Greedy算法差别不大，几乎相同。

在复杂度分析中，只考虑加法和乘法，单位为flops，假设文中提出算法中的排序使用的是快速排序方法［7］。为了简单，由于无论在Greedy算法和新提出的自适应调制算法的2种方案中都需要使用SVD分解，所以其复杂度将不予考虑。图4为复杂度比较图。

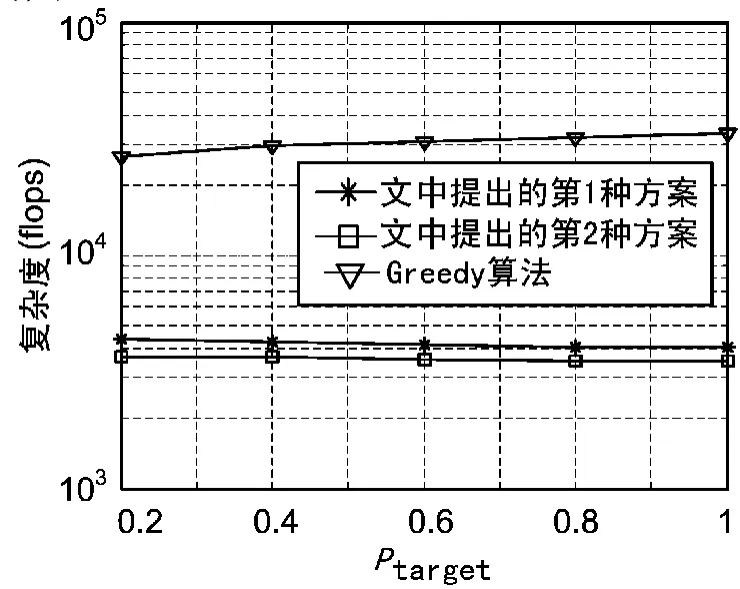
图4 复杂度比较图

由图4可知，新提出算法的复杂度是Greedy复杂度的10－1，在性能相差较小的情况下，复杂度降低非常大，故自适应调制算法在实际系统中能够广泛应用。

4 结束语

提出了一种在误比特率和传输功率一定的情况下最大化传输速率的算法，通过仿真结果可以看出，所提出的新算法在性能上与Greedy算法几乎一致，但是复杂度却大大降低，是Greedy算法的10－1，解决了Greedy算法性能好但在实际中由于高复杂度而不能使用的缺陷，在以后的工作中可以得到广泛应用。

［1］FOSCHINI G J， GANS M J. On limits of wirelesscommunications in a fading environment when using multiple antennas ［J］. wireless Personal Communications，1998，6(3)：311 －335.

［2］BOLCSKELH，ZURICH T.MIMO-OFDM wireless systems：basics，perspectives and challenges ［J］.IEEE Trans.On Wireless Commu.，2006，13：31 －37.

［3］SAMPATH H，TALWAR S，TELLADO J，et al.A Fourth-Generation MIMO-OFDM Broadband Wireless system：Design，Performance，and Field Trial Results［C］∥IEEE Commun.Mag.，2005.1：154 －172.

［4］AMPATH H，TALWAR S，TELLADO J，et al.Broadband wireless system：Design，performance and field trial results［J］.IEEE Commu.，2002(9)：143 － 149.

［5］FAN L Y，HE C，FENG G R.Optimal bit allocation adaptive modulation algorithm for MIMO system ［J］.Journal of Communication and Networks，2007，9(2)：136 －140.

［6］CHUNG S T，GOLDSMITH A J.Degrees of freedom in adaptive modulation：a unified view ［C］∥IEEE Trans.Commun.，IEEE Inc，49(9)：1561 －1571，2001.

［7］BAASE S，GELDER A V.Computer algorithm：introduction，design and analysis［M］.North Asia ：Higher education press and Pearson education，1999：149－171.