基于正则化方法的Hull－White 短期利率模型参数估计

江 良，忻丁耀

（1.同济大学 数学系，上海200092；2.莆田学院 数学系，福建 莆田351100；3.同济大学 教育技术与计算中心，上海200092）

众所周知，Vasicek[1]首先提出均值回归短期利率模型.为了更好地拟合市场数据，Hull等[2]延拓了Vasicek模型，考虑所有的参数都是时间变量的函数.但是Brigo等[3]注意到该模型中波动率函数很难通过市场上债券数据拟合.因此，本文将考虑长期回归均值是时间变量的Hull－White模型[2]，该模型拟合的效果将会得到很大的改善.Brigo等[3]已给出关于长期回归均值函数显示表达式，但其表达式依赖于远期瞬时利率及其导数.根据Hanke等[4]论述，数值方法求解导数是一个不稳定性问题，因此不能直接通过导数估计长期回归均值.正则化方法应运而生.

假设市场报价完全匹配理论价格.通过数学技巧，原问题可转化为求解第一类Volterra积分方程[5].这类积分方程数值解一般是不稳定的.本文将使用正则化方法来求解这类问题，归咎于正则化方法是稳定的数值计算过程.该方法通过引入罚函数来控制数值结果的稳定性[6].因此，通过债券价格估计Hull－White模型中参数问题有必要使用正则化方法.在本文中，将使用微分算子作为罚函数，相对于标准的Tikhonov正则化[6]，这类罚函数允许被估计函数具有一定光滑性.

1 利率与债券定价模型

首先，假设短期利率r在风险中性测度下满足如下的随机微分方程[3]：

其中a，σ为常数，θ（t）是关于时间的函数，W（t）为标准的Brown运动.基于式（1），在时间t时刻，到期日T支付为1单位的债券价格有如下表达式：P（t，T）＝P（t，T；a，σ，θ，r）＝A（t，T）e－B（t，T）r，其中A＝A（t，T）和B＝B（t，T）表达式如下[3]：

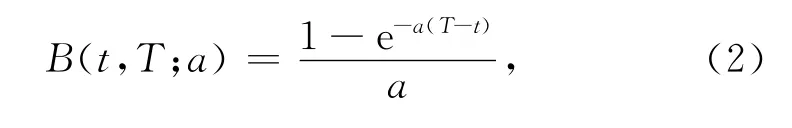
设当前时刻（t＝0）到期日为T的市场债券价格的收益率R（0，T）满足等式PM（0，T）＝e－R（0，T）T，0≤T≤T＊，其中PM（0，T）为市场价格，T＊是债券价格最大的到期日.两边取对数，可获得fM（0，T）·＝lnPM（0，T）＝－R（0，T）T.定义范数和内积：

2 参数估计计算方法

设lnP（0，T）＝fM（0，T）.根据式（2）和（3），得到：

其中

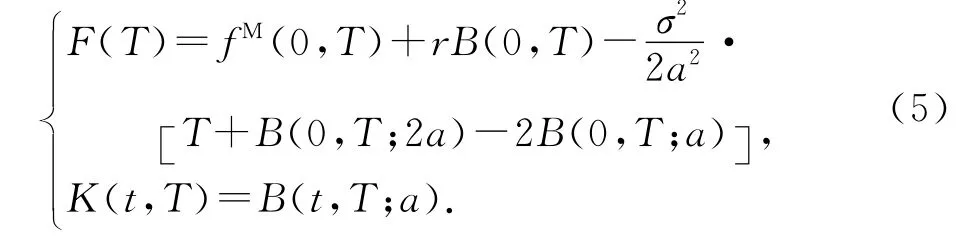
注意式（4）是第一类Volterra积分方程，其中F（T）和K（t，T）（数学上K（t，T）称为核）是已知的函数，θ（t）是待求解的函数.

为了简化问题，设Κ为积分算子，即Κθ·＝相应函数θ（t）的解能通过下面的优化问题获得（T∈[0，T＊]）：

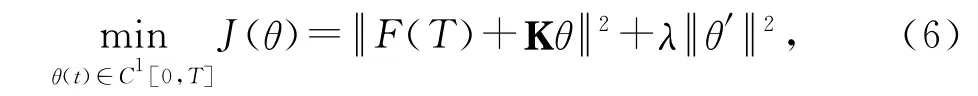
其中初始条件θ0＝θ（0），λ是正则化参数.设Fδ（T）为扰动的数据且

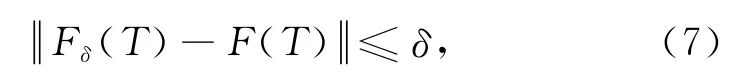
式中，δ是数据的测度误差.

定理1 设θλ，δ和θλ分别是式（6）的极小值对应于Fδ（T）和F（T），从而有

其中eδ（t）＝θλ，δ（t）－θλ（t）.

证明 设0≤α≤1，那么θλ＋αeδ∈C1[0，T].由于θλ是问题（6）的极小值，即

类似地，能够得到

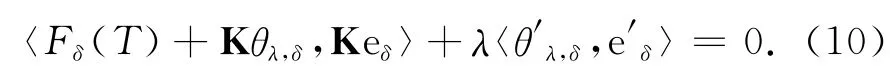
把式（9），（10）相减可以获得

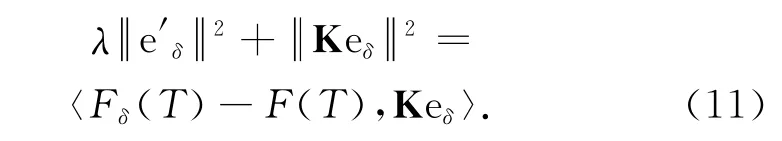
定理2 设θ＊是式（4）的精确解且是有界函数.设正则化参数λ满足

假设序列 ｛θλk，δk｝中的每一元素是式（4）的解，其中δk及λk·＝λ（δk）满足假设式（12）.那么每一收敛子列极限值是式（4）的解而且如果式（4）的解是唯一的其极限为θ＊.

证明 由于θλk，δk是优化问题（6）的解，因此可以得到

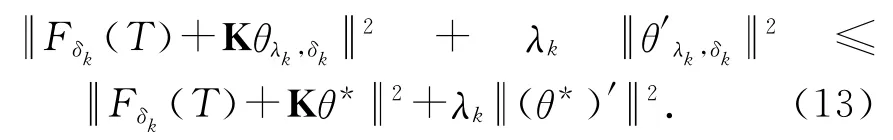
由不等式（13）及在定理2中的假设，有

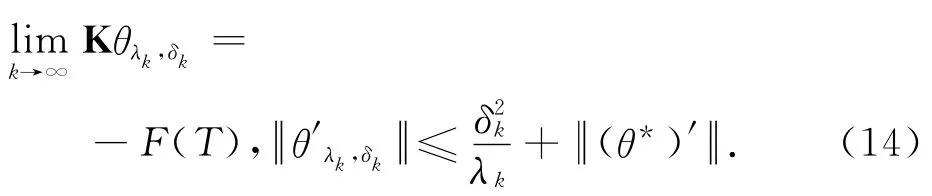
应用Poincare不等式，式（14）表明了θλk，δk是一致有界且等度连续函数.由于算子K是一致有界线性算子，根据Arzela－Ascoli定理[8]，存在收敛子列其极限满足式式（4）.若式（4）的解是唯一，由于收敛子列极限是等同的，因此其极限值为θ＊.定理证毕.

设ΔT＝Ti－Ti－1，i＝1，…，N，其中T0＝0和TN＝T＊.N表示总的观察数据数.假设θ（t）·＝θi－1，Ti－1≤t≤Ti，其中θ0定义在T0＝0时刻.使用中心差分离散格式近似积分方程，

基于数学归纳方法，设Θi－1＝ ｛θ0，θ1，…θi－1｝是已知的，i＝1，…，N，式（6）的离散格式为

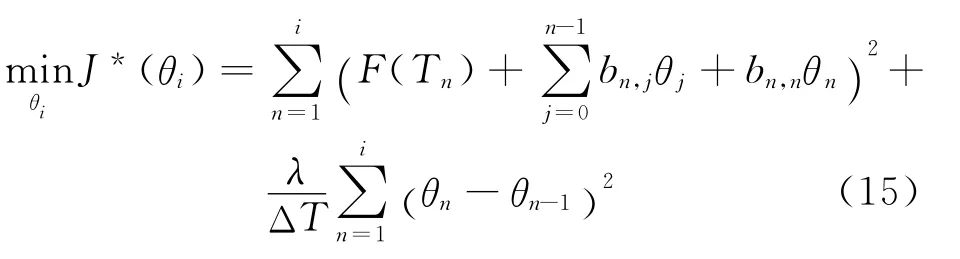
通过对（15）关于θi求导数，可得

其中λ·＝λ／ΔT.在给定Θi－1条件下，式（15）是关于θi的一元二次方程.因此，由（16）所求的解一定是极小值.

3 数值算例

3.1 模拟结果

设a＝0.01，r＝0.03，σ＝0.1假设θ（t）＝（0.001＋0.1t）exp（－0.9t）＋0.009.其初始条件θ0＝0.01.定义根均值误差（root mean square error，RMSE）为其中θi是数值解，θ（ti）是精确解.为了简化问题，本文将考虑ΔT＝0.5年.

图1显示不同正则化参数所对应lnRM的值.从图1可知正则化参数应取机器精度.图2显示了数值结果和精确解.显然，当正则化参数很小时和直接数值求解几乎没有任何的区别.当λ＝0时，RM＝1.875 7×10－14；当λ＝1×10－9时，RM＝2.324 2×10－7.虽然从图形中无法明显地看出正则化方法和直接求解方法（λ＝0）的区别，但是下面数值结果将呈现正则化方法的优势.

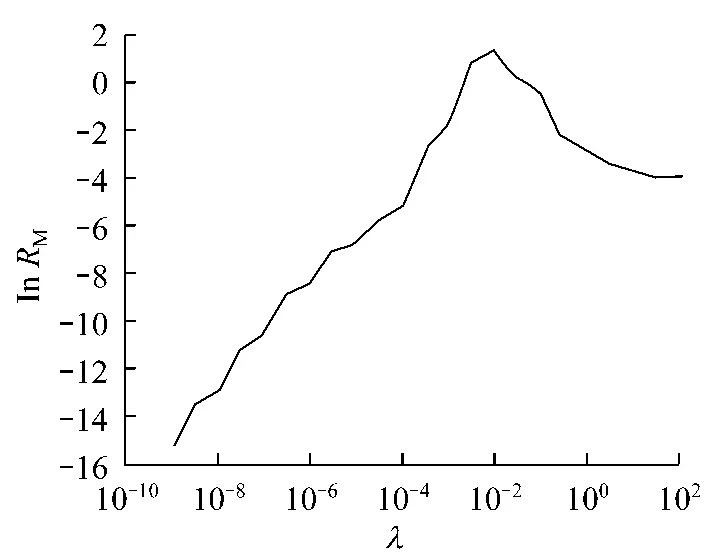
图1 不同正则化参数选取所对应的ln RM的值Fig.1 The values of ln RM for different regularization parameters

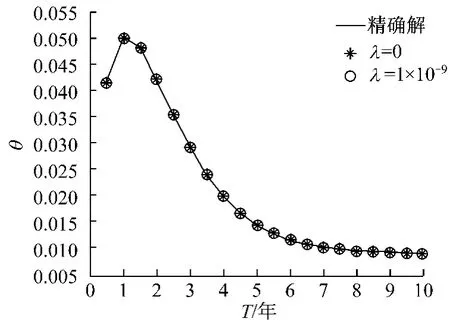
图2 比较精确解及数值解（λ＝0及λ＝10－9）Fig.2 Comparision of the exact solutions and numerical solutions（λ＝0 andλ＝10－9）

设噪声的数据通过表达式fδ，M（0，T）＝fM（0，T）（1＋δz）产生，其中δ是常数，z服从均值为0，方差为1的标准正态分布的随机数.

图3描述对于不同δ取值分别使用正则化方法和直接求解方法所对应的对数RMSE估计.显然，通过观察图形，直接求解方法和正则方法都是稳定的.然而当数据带有较大的噪声时，正则化方法具有更好的数值结果.

图3 对于不同δ取值所对应的对数根均值误差估计Fig.3 The values of ln RM are plotted for differentδ

3.2 实证结果

考虑美国国债每天交易2011年6月1号收益率数据（来源于http：／／www.ustreas.gov）.最大的到期日为10年.设ΔT＝0.5年，r＝0.03%.由于实际的报价仅只在一些节点上.因此通过三次样条差值方法补上一些缺失的数据.其数据结果呈现在图4中.参数a和σ取值将基于标准的最小二乘法来估计.θ0将基于0≤T＜T1的数据通过最小二乘法的方法来估计.为了刻画拟合的结果引入RMSE为

基于Vasicek模型，参数估计值分别为θ＝0.009 218，a＝0.113 4，σ＝0.020 39及相应的RMSE值为0.004 031.其长期均值年收益率为θ／a＝8.13%.图5给出相应的数值解和市场数据的比较.从图5可知，对于长期的数据，Vasicek模型拟合比较好，但是短期的数据其误差相当大.这就说明了常数θ值可能导致模型误判.因此考虑时间变量长期回归均值是有必要的.

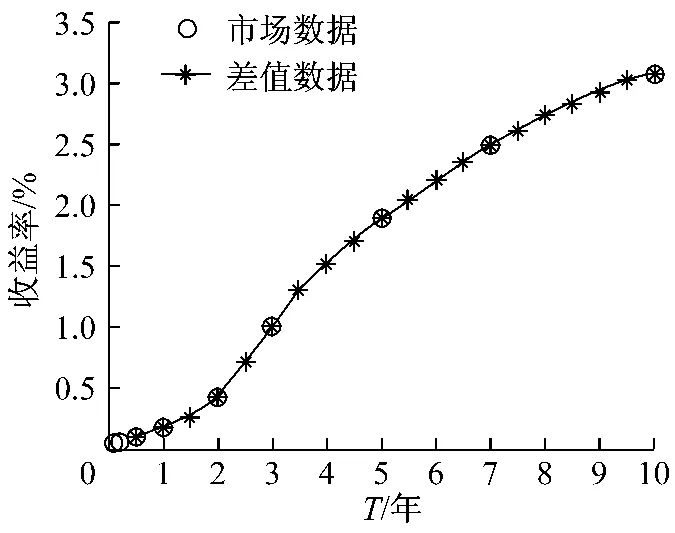
图4 比较市场收益率数据和插值数据Fig.4 Comparision of the mar ket yield curve and the cubic interpolation results

图5 基于Vasicek模型，数值结果和市场数据的的比较Fig.5 Comparision of the exact solutions and the mar ket qutoes

类似上一节的模拟结果，通过最小RMSE值选取其参数.图6显示不同λ值所对应对数RMSE值.从图形可知，λ没有最小值，极端的情况λ＝0.若基于拟合考虑，正则化方法和直接求解方法没有区别.但正则化方法能够通过调整正则化参数控制误差精度和数值结果稳定性.如通过数值测试，当λ＝10－4时，RM＝1.993 2×10－5.其保留4个有效数字，在实际应用中是可接受的.若λ更大，拟合效果较差；若λ更小，后面的有效数字估计是没有用的.相应的数值结果被呈现在图7中.而当λ＝0时，RM＝4.670 9×10－18，因为对于收益率不需要估计到这多的有效数字.

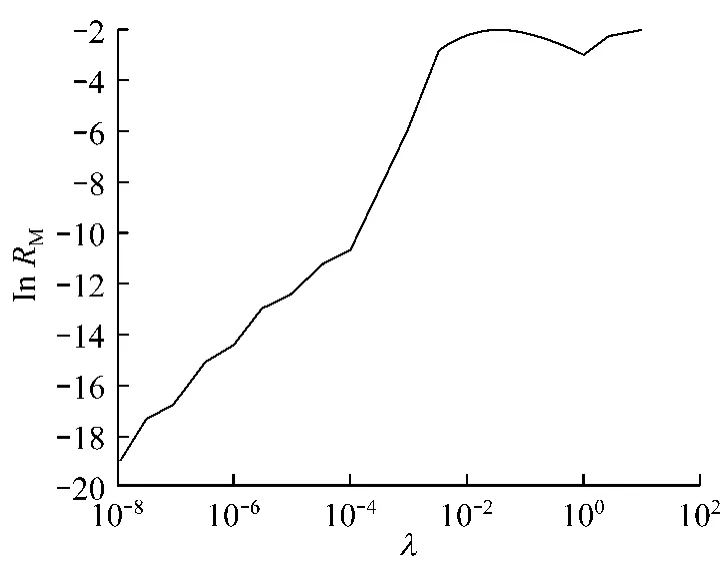
图6 对于不同的λ的值所对应ln RM误差估计Fig.6 Esimates of ln RM for differentλ

图8显示市场收益率数据和数值解及θ的数值结果.当λ＝10－4时，其数值结果相对比较稳定.同时当λ＝0，θ有一部分是取负数并呈现激烈的震荡，而λ＝10－4几乎都是正的数.从实际应用价值考虑，其数值结果表明基于Hull－White模型有必要使用正则化方法.另一方面，比较Hull－White模型和Vasicek模型，显然考虑Hull－White模型改善拟合的结果.

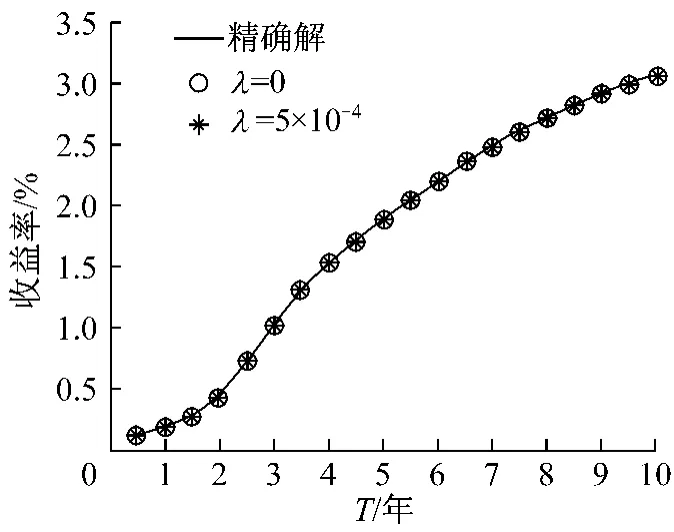
图7 比较收益率市场数据和数值解（λ＝0和λ＝5×10－4）Fig.7 Comparision of the mar ket yield curve and the numerical solutions（λ＝0 andλ＝5×10－4）

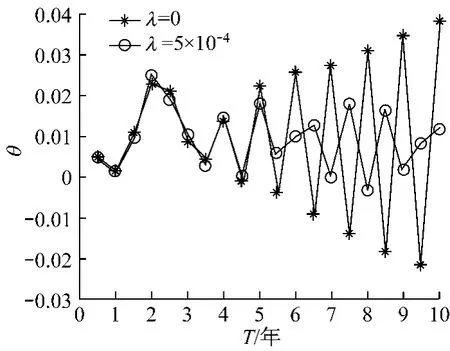
图8 比较不同的正则化参数θ（t）的数值结果Fig.8 Comparision ofθ（t）with the cor responding regularization parameters

4 结论

本文提出一种有效的正则化方法估计Hull－White模型中的参数.证明了该计算方法稳定性和收敛性.通过数值模拟结果确认了基于Hull－White模型正则化方法计算的有效性.最后实际应用表明了正则化方法更加有效并更符合实际意义.

致谢

感谢同济大学数学系姜礼尚教授对本文提出建设性的意见.

[1] Vasicek O.An equilibrium characterization of the term structure[J].Journal of Financial Economics，1977，5（2），177.

[2] Hull J，White A.Pricing interest－rate－derivative securitites[J].The Review of Financial Studies，1990，3（4），573.

[3] Brigo D，Mercurio F.Interest－rate models：theory and practice[M].Berlin：Springer－Verlag，2006.

[4] Hanke M，Scherzer O.Inverse problems light：numerical differentiation [J].The American Mathematical Monthly，2001，108（6）512.

[5] Linz P.Analytical and numerical methods for Volterra equations[M].Phiadelphi：SIAM，1985.

[6] Engl H W，Hanke M，Neubauer A，et al.Regularization of inverse problems [M ]. Dordrecht： Kluwer Academic Publishers，1996.

[7] Adams A R，Fournier J J F.Sobolev spaces [M].Beijing：Beijing World Publishing House，2009.

[8] Nair M L.Linear operator equations[M].Singapore：World Scientific，2009.