基于2.5维有限元算法的边界处理及网格划分
周 彪,谢雄耀,李永盛
(1.同济大学 岩土及地下工程教育部重点实验室,上海200092;2.同济大学 地下工程系,上海200092)
波数有限元法或2.5维有限元法是在假设实际的铁路、地铁、隧道结构和土体地质条件在长度方向几何形状和材料性质不变的前提下.将其在无限长运行方向用傅立叶变换等周期化方法将其分解成一系列沿该方向传播的简谐波.在计算每个简谐波时,只需要对结构-土体的横截面进行离散.从而在利用2.5维方法模拟列车荷载作用下轨道、隧道以及周边环境振动的研究中,既克服了二维平面模型不能模拟移动荷载作用下周围地基中波动传播的马赫辐射效应的瓶颈以及无法考虑列车运行方向的荷载影响的缺点,其计算量又明显低于3维有限元分析模型.因而被国内外学者大量采用.
该方法是Hwang等[1]在研究地震行波作用下地下结构动响应时提出的,之后被国内外学者引入到交通荷载作用下地基振动以及地下轨道交通环境振动的研究中.同时该方法在基于有限元基础之上,其边界模拟上除了采用最初的粘滞透射边界外,边界元和无限单元法等技术也被引入并与之进行耦合.其中 Yang和 Huang[2-4]用2.5 维有限元法分析了移动荷载作用下地基的动力响应问题,并分析了高速列车在弹性地基上运行的动力响应以及沿着铁路线的空沟的隔振.边学成等[5-6]采用2.5 维有限元结合边界元法分析了列车和地铁荷载作用下结构-地基的动力响应问题.谢伟平等[7]指出列车运行时的振动问题主要是由移动荷载的自振与移动位置的变化引起的,并进行了相关分析,应用了2.5维有限元方法,对移动方向进行波数积分求解,并考虑了地基土不同性质的影响.Sheng等[8]对波数有限元法和波数边界元法应用于列车运行产生的大地振动问题作了详细的推导.另外Gupta等[9]以及国内刘维宁等[10]将Floquet技术应用于有限元-边界元(FEBE)耦合分析.
上述方法中除边界元外,其他边界处理方法均对有限元模拟区域及网格大小提出要求,Yang等[11]在利用有限元和无限元模拟二维振动问题时分析了有限元模拟区域大小及网格质量对模拟结果的影响,但未对使用2.5维技术过程中,上述参数的影响做出分析,因而本文基于2.5维方法,通过 Matlab编制程序,分别研究了粘滞阻尼边界和无限元边界条件下上述参数的影响,并对上述参数的合理选择提出建议.
1 2.5维有限元方法
1.1 基本假设
如图1所示,2.5维方法假设沿z方向以速度c移动的荷载形式为

式中,Ψ(x,y)Φ(z-ct)反映荷载的空间特征,q(t)为其时间域特征,其可由诸多周期波组合而成.若假设q(t)=exp(iω0t),经由傅立叶变化其在频域波数域内的表达式为
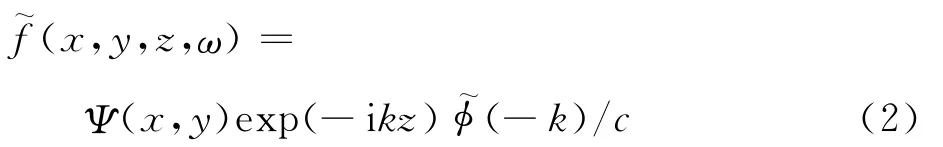
ω0)/c,其中ω为角频率,k为波数.同理,可以通过式(3)所示逆变换将其重新转化为时空域.
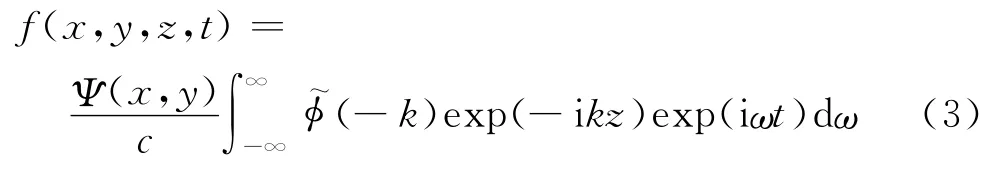
假设沿z方向地质条件、几何形状和材料性质均不变,且动力响应为线性,则在荷载Ψ(x,y)·exp(-ikz)exp(iωt)作用下,其频域内动态响应解可表示为D(ω)exp(-ikz)exp(iωt).
由此,若可求取D(iω)值,则地基时域内三维动态响应可通过式(4)所示变化求得.而其可以通过运用数值方法对某一z值条件下的xoy截面进行网格划分求得,其具体方法将在节1.2中阐述.
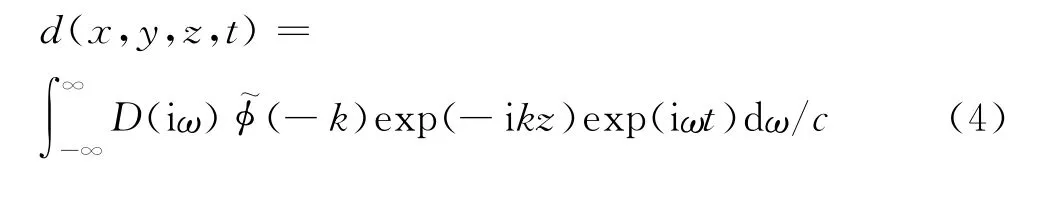

图1 2.5维模型示意图Fig.1 The layout of the 2.5D method
1.2 波动方程的2.5维数值表达式
根据1.1所述,在荷载 Ψ(x,y)exp(-ikz)·exp(iωt)作用下,将其位移响应值定义为
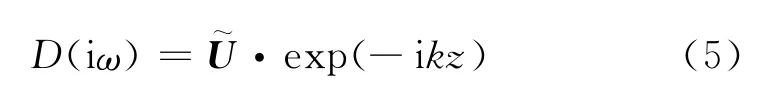
根据Navier方程,在频域内的三维弹性土体介质波动方程可表示为
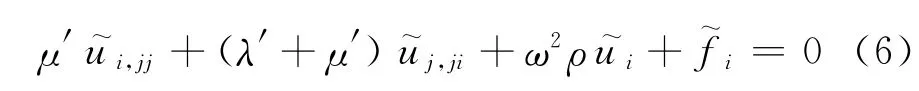
其中采用复系数的Lame常数λ′和μ′来考虑土体阻尼对波动传播的影响.
结合式(5)—(6),根据小变形假设,三维土体单元的几何方程可表示为

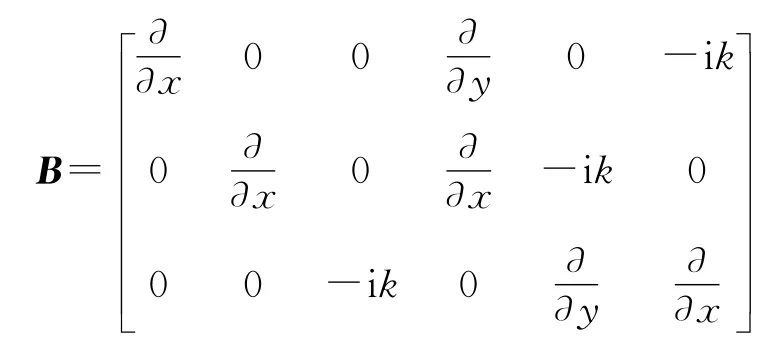
同时根据应力—应变关系得到:


采用普通8节点等参单元对xoy平面进行离散化处理,并运用相关边界条件,根据伽辽金(Galerkin)法即可得到在频域中的离散方程:
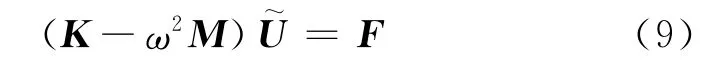
式中,质量矩阵M、刚度矩阵K和荷载矩阵F分别表示为
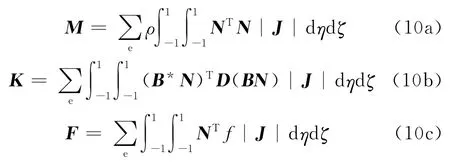
其中:
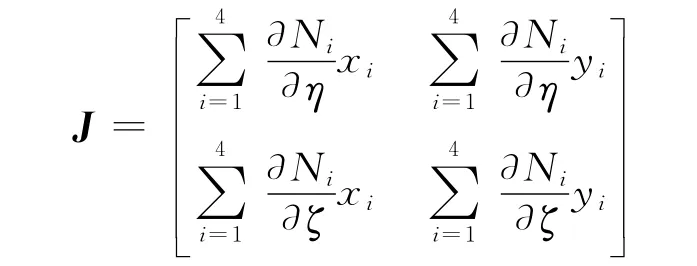
式中:ρ为单元材料密度;η及ζ为局部坐标,上标‘*’表示共轭矩阵,上标‘T’表示矩阵转置.通过求取式(9),便可获得U~,亦即D(iω)值.
2 边界处理方法
在分析动荷载作用下地基瞬态响应过程中,由于有限元方法中网格划分范围以及单元大小是有限的,难以直接对无限地基进行模拟,故必须建立一种合适的人工边界来阻止外行波反射回有限元单元表示的近场区域中.在第一章所述边界处理上,无限元和透射边界都对有限元模拟区域或网格的大小有不同程度的要求.因而本文就各类边界处理方法及其相关对近场有限元网格的要求做出阐述.
2.1 粘滞阻尼透射边界
所谓粘滞阻尼透射边界,是一种运用与频率相关的黏壶单元来模拟无限地基,如图2所示,图中,kx=kz=ρvs,ky=ρvp,vs和vp分别为剪切波(S波)和压缩波(P波)波速.尽管这种黏壶单元对外行波能量的吸收不但取决于地基土体的材料特性,同时也与外行波的频率有关,近来的研究表明这种吸收单元在实际运用中非常有效[6].
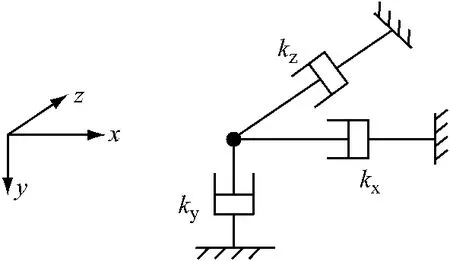
图2 频率相关黏壶透射边界Fig.2 Frequency related sticky pot of transmitting boundary
该吸收单元的系数由半无限区域的材料特性来决定,在频域内,单元节点上的外加集中力与变形速率之间的关系可以表示为
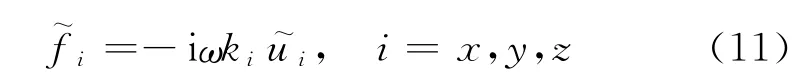
2.2 无限元边界
杨永斌[2]提出运用2.5维FE-IFE耦合算法来模拟振动波传播,如图3所示,其采用了较为精确的形函数,并且坐标形函数与位移形函数不一致,坐标形函数具体表达式如下:

位移形函数表示为
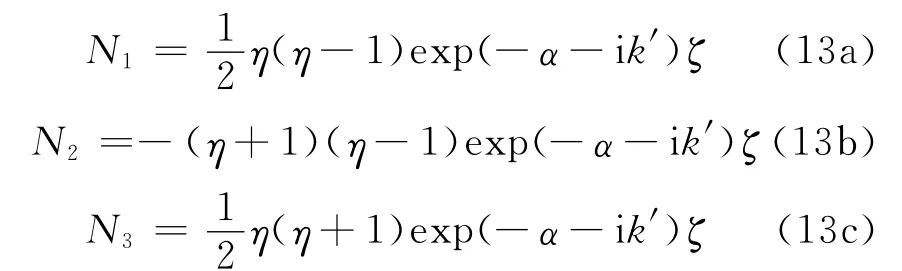
式中:α,k’分别为单元在局部坐标系中的幅值衰减系数和名义波数,分别表示单元在局部坐标系中的幅值衰减特性和相位滞后特性.杨永斌等[2]详尽阐述了其数值的选择,结合赵崇斌等[12]中关于中节点位置选择原则可以定义上述参数.其中波数k’的选择有别于一般的二维无限元的取值,其值对应于P波,S波,瑞利波(R波)的定义如下:
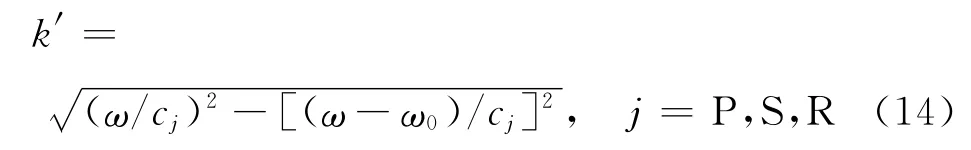
其整体坐标与局部坐标之间的转换如图3所示.
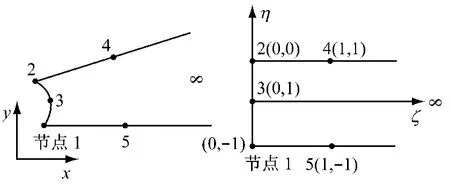
图3 无限单元整体和局部坐标系Fig.3 Global and local co-ordinates of the infinite element
按照有限元的伽辽金(Galerkin)法,最终也得推得如式(7)—(10)所示频域-波数域中与2.5维有限元一致的形式,但由于无限元在ζ方向上积分范围为[0,∞],因而其积分方法不能采用常用的高斯积分准则,张楚汉等[13]给出了相应的积分方法,本文采用该方法对式(10)进行积分得到相应的质量、刚度及荷载矩阵.
3 不同边界条件对有限元网格选择的影响
为了检验文中所提方法在Matlab中实现的准确性以及网格划分质量和范围的影响,本文利用Ansys建立如图4所示模型,图中L为单元最大尺寸,R为荷载作用点距离有限元边界距离,中间白色区域为8节点有限元单元网格,边界灰色区域为无限元单元.如图4,在模型中央施加移动荷载f(x,y,z=0,t),根据1.1节所述原理,ω 取为32 Hz,ω0取为0 Hz,移动速度取为120 m·s-1.通过从 Ansys中输出荷载、单元和节点信息并输入到Matlab中,基于上述2.5维FE-IFE耦合方法再将有相关单元信息进行重组,得到相应的质量、刚度及荷载矩阵,根据式(9)即可求取其在频域范围内的振动响应解.

图4 有限元和边界元模型及网格划分Fig.4 The modeling of the finite element method(FEM)and infinite element method(IFE)
图4所示模型中材料弹模取为2×107MPa,泊松比取为0.25,密度为2 000 kg·m-1,阻尼比为0.05,通过改变模型尺寸和网格大小,计算地基土的动力响应.选取如图4所示距离地表0.9 m所示测线上频域范围内土体三向位移解,并乘以2πG/c以求得量纲—值,其中G为剪切模量.将其结果与Eason所提出的解析解[14]进行比较,以检验网格质量对模拟结果的影响.
3.1 不同边界下有限元模拟区域尺寸的选择
针对粘滞边界和无限元边界两种情况,根据节2.1—2.2所述方法求解在简谐荷载作用下地基响应问题.如图5,当有限元模拟区域R取为1.5倍瑞利波波长时(根据材料参数,瑞利波波速约为4.48 m,以下均表示为λ),测线处粘滞边界和无限元边界的计算结果与Eason解析解的对比情况如图5所示.

图5 不同边界对竖向位移解的影响Fig.5 Effect of different boundary condition on vertical displacement
从图5中可以看出无限元边界较粘滞边界有更好的模拟效果.在此工况下,无限元解已经与解析解基本吻合,而粘滞边界仍有较大的偏差,特别是距离边界处这种趋势更加明显.同时可以看出虚部解偏差更为显著,所以下文分析中对某些工况只比较虚部解的差异来确定影响程度的大小.
为更好分析粘滞边界条件下模拟尺寸的影响,如图6所示,分别选取R为0.8λ,1.5λ,2λ以及4λ,比较测线竖向位移的虚部解的差异.从图中可以看出所有曲线都能反映波动的大致趋势.但小于1λ时偏差较大,当模拟距离大于2λ时,其结果才与解析解较吻合,但仍有偏差,所以如运用粘滞边界条件时,应将模拟区域大于2λ,如需精确解要将范围扩至3λ~4λ.
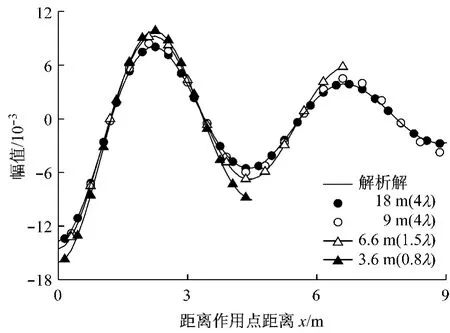
图6 粘滞边界条件下有限元模拟尺寸对竖向解的影响(虚部)Fig.6 Effect of mesh size R on vertical displacement(image part) on condition of using visco boundary
以上可以看出,在相同条件下运用无限元边界将有更好的效果.因而本文以下着重分析在无限元边界条件下网格大小及模拟区域对计算结果的影响.
3.2 无限元边界有限元模拟区域尺寸(R)的选择
在运用无限元边界条件下,分别选取模拟范围为0.5λ、0.8λ、1.5λ以及2λ,通过比较测线x,y,z方向上位移分析模拟尺寸的影响.
图7分别描述了不同长度模拟区域下竖向(y向)实虚部解.从结果上看,模拟区域的大小对虚部解影响较大.从结果上看当模拟范围取为0.8λ时,结果虽与解析解偏差已经很小.所以当仅关注作用方向上位移时,模拟区域可超过1λ即可满足精度要求.
图8—9分别显示了x方向和z方向上位移虚部解与解析解的差异,从结果上看,模拟区域对其影响要明显大于竖向位移.特别是z方向即荷载移动方向上,当L<λ时,其偏差较大,仅当模拟范围超过1.5λ时才发现数值解收敛并与解析解吻合.同时发现x方向上边界有反射现象发生,这主要是因为在无限元边界参数中波数参量的选择只能考虑一种波,而实际上地基土中存在有P,S以及R波,从而会对结果造成影响.因而在模拟x和z向土体响应时,其模拟范围应该超过1.5λ.
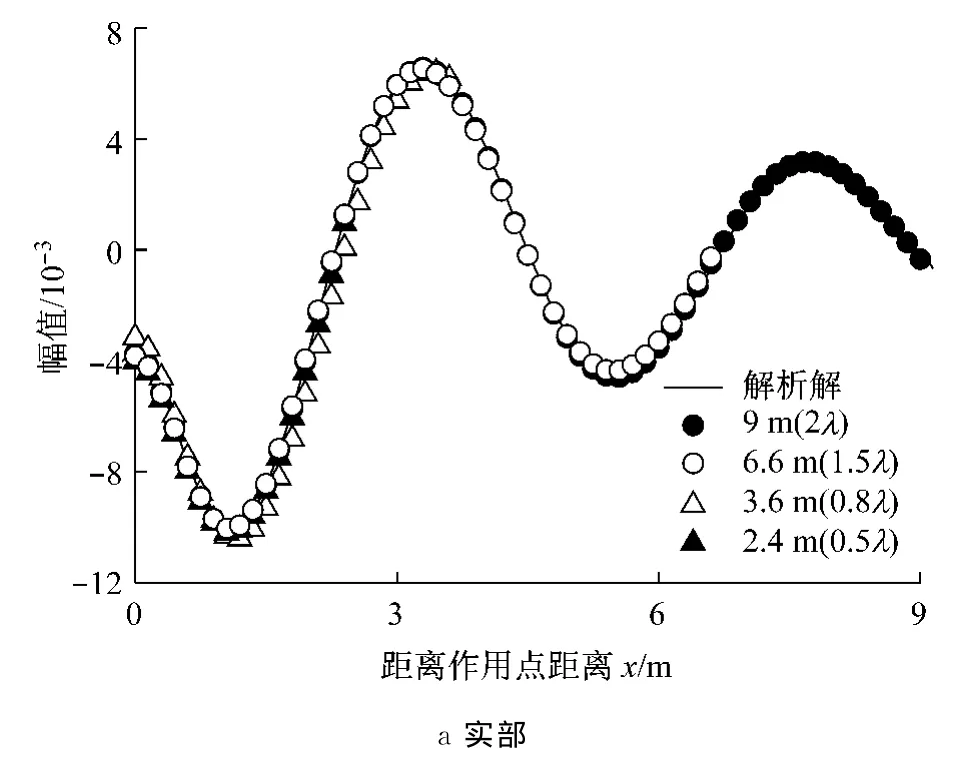
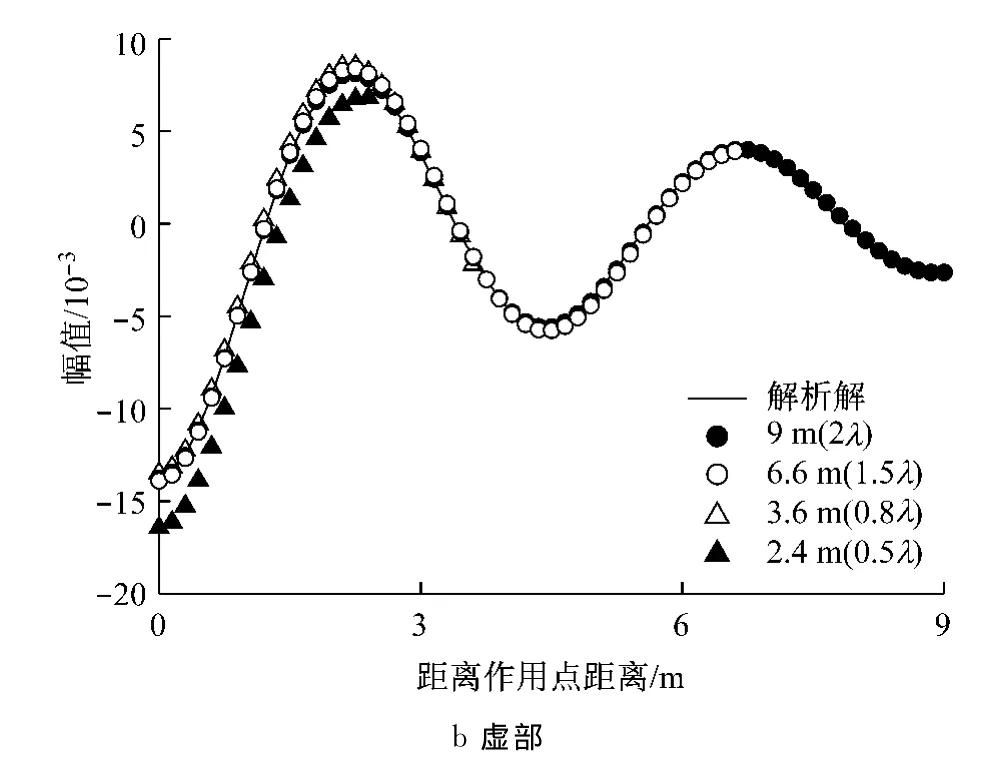
图7 无限元边界条件下有限元模拟尺寸R对竖向解的影响Fig.7 Effect of mesh size R on vertical displacement on condition of using infinite element boundary
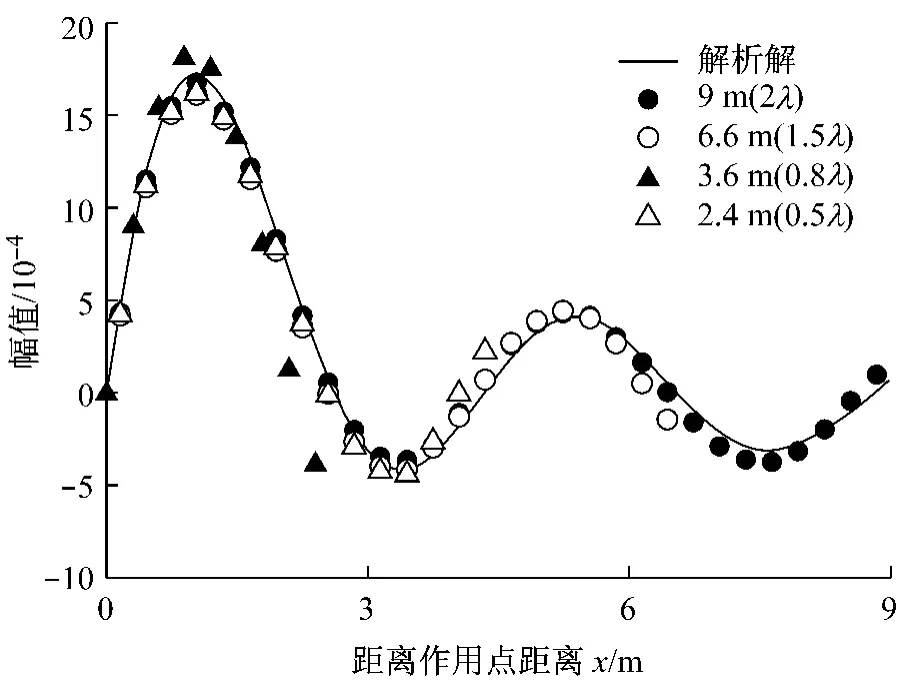
图8 无限元边界条件下有限元模拟尺寸R对x向解的影响(虚部)Fig.8 Effect of mesh size R on x direction displacement(image part)on condition of using infinite element boundary
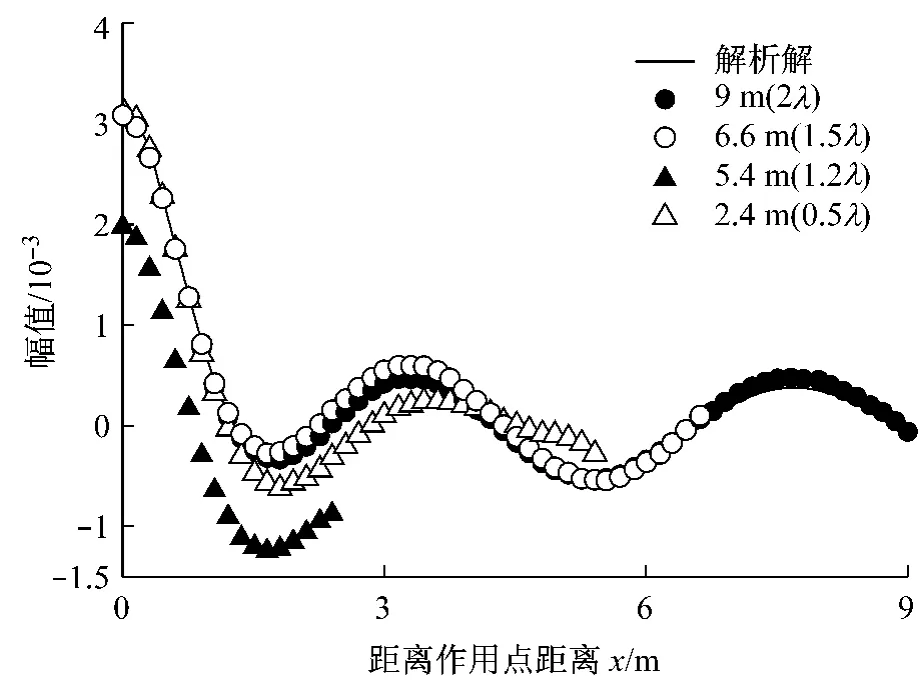
图9 无限元边界条件下有限元模拟尺寸R对z向解的影响(虚部)Fig.9 Effect of mesh size R on z direction displacement(image part)on condition of using infinite element boundary
3.3 无穷元边界有限元网格大小的选择
从以上分析可以看出,当模拟范围为2λ时,数值解能满足精度要求,因而本文在模拟范围为2λ前提下,对不同网格大小的影响做出分析.
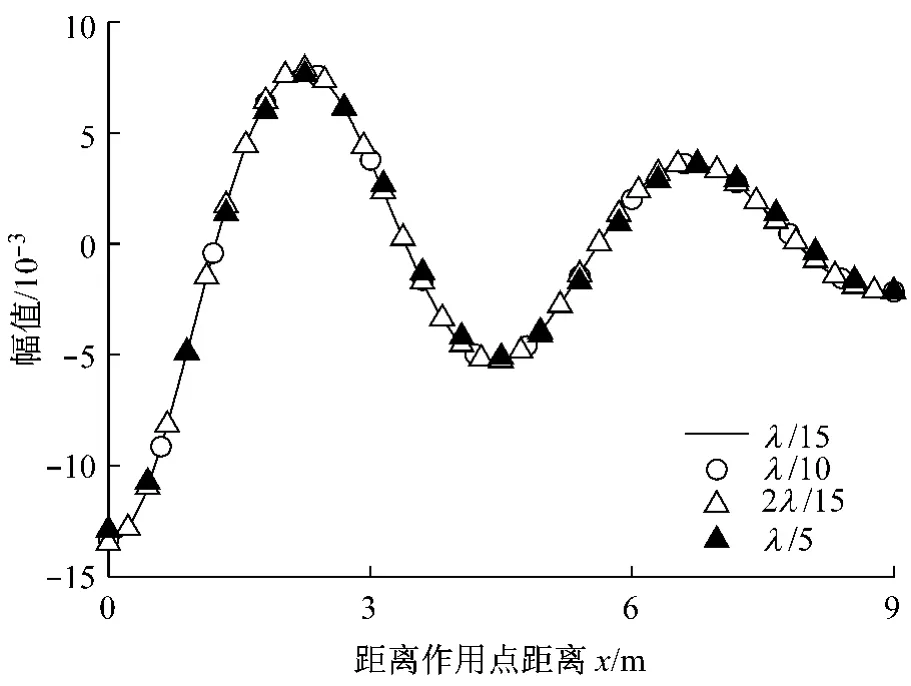
图10 无限元边界条件下有限元网格大小L对y向解的影响(虚部)Fig.10 Effect of element size L on y direction displacement(image part)on condition of using infinite element boundary
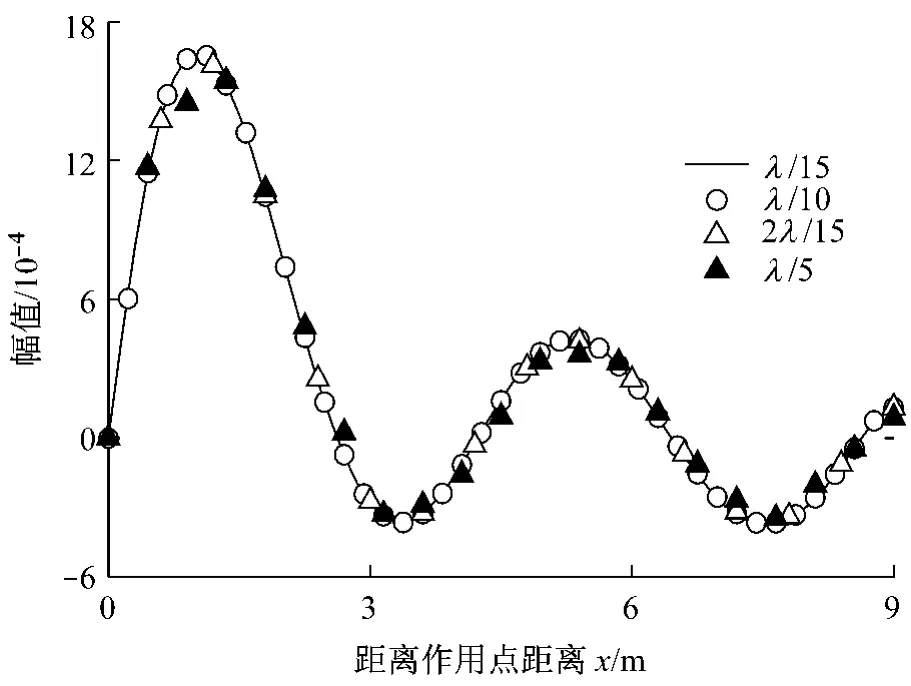
图11 无限元边界条件下有限元网格大小L对x向解的影响(虚部)Fig.11 Effect of element size L on x direction displacement(image part)on condition of using infinite element boundary
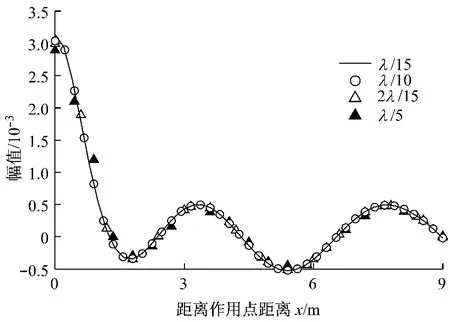
图12 无限元边界条件下有限元网格大小L对z向解的影响(虚部)Fig.12 Effect of element size L on z direction displacement(image part)on condition of using infinite element boundary
图10—12分别为x,y,z向位移的虚部解,从结果上看,网格大小的影响要小于模拟范围,其影响大多集中在荷载作用点附近.从图中结果可以得出结论,当网格大小超过λ/10时即能满足精度要求.
4 结论
本文基于Matlab平台,编写了适用于计算和预测列车振动波传播和衰减的2.5维计算模块,讨论了粘滞边界以及无限元边界条件在不同有限元模拟范围以及网格大小对结果的影响,并得出以下结论:
(1)在运用2.5维计算方法模拟地基响应过程中,无限元边界较粘滞边界有更好的适用性,其所需要的有限元近场模拟区域更小.
(2)在运用无限元模拟地基响应时,为获取高精度解,其有限元近场模拟区域边缘距离荷载作用点必须超过某一数值,对于竖向响应,其必须大于1倍瑞利波波长.研究横向和侧向响应,应大于1.5倍瑞利波波长.
(3)在模拟过程中,网格大小对计算结果精度影响较小,当网格大小大于0.1倍瑞利波波长时即可满足计算精度要求.
[1] Hwang R N,Lysmer J.Response of buried structures to traveling waves [J].Journal of Geotechnical Engineering,ASCE,1981,107(GT2):183.
[2] Yang Y B,Hung H H.A 2.5D finite/infinite element approach for modelling visco-elastic bodies subjected to moving loads[J].International Journal for Numerical Methods in Engineering,2001,51:1317.
[3] Yang Y B,Hung H H.Chang D W.Train-induced wave propagation in layered soils using finite/infinite element simulation[J].Soil Dynamic and Earthquake Engineering,2003,23(4):263.
[4] Hung H H,Yang Y B,Chang D W.Wave barriers for reduction of train-induced vibrations in soils[J].Journal of Geotech and Geoenvironment Engineering,ASCE,2004,130(12):1283.
[5] 边学成,陈云敏.基于2.5维有限元方法分析列车荷载产生的地基波动 [J].岩石力学与工程学报,2006,25(11):2335.BIAN Xuecheng,CHEN Yunmin.Ground vibration generated by train moving loadings using 2.5D finite element method[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(11):2335.
[6] 边学成,陈云敏,胡婷.基于2.5维有限元方法模拟高速列车荷载产生的地基振动[J].中国科学,2008,38(5):600.BIAN Xuecheng, CHEN Yunmin, HU Ting. Numerical simulation of high-speed train induced ground vibrations using 2.5D finite element approach[J].Science in China Press(G),2008,38(5):600.
[7] 谢伟平,孙洪刚.地铁运行时引起的土的波动分析 [J].岩石力学与工程学报,2003,22(7):1180.XIE Weiping,SUN Honggang.FEM analysis on wave propagation in soils induced by high speed train load [J].Chinese Journal of Rock Mechanics and Engineering,2003,22(7):1180.
[8] Sheng X,Jones C J C,Thompson D J.Modelling ground vibration from railways using wave number finite-and boundary element methods[J].Proceedings of the Royal Society A,2005,461:2043.
[9] Gupta S,Degrande G,Lombaert G..Experimental validation of a numerical model for subway induced vibrations [J],Journal of Sound and Vibration,2009,321(3-5):786.
[10] 刘卫丰,刘维宁 地铁振动预测的周期性有限元-边界元耦合模型[J].振动工程学报2009,22(5):480.LIU Weifeng,LIU Wenning.A coupled periodic finite elementboundary element model for prediction of vibrations induced by metro traffic[J].Journal of Vibration Engineering,2009,22(5):480.
[11] Yang Y B,Kuo S R,Hung H H.Frequency-independent infinite element for analyzing semi-infinite problems[J].International Journal for Numerical Methods in Engineering,1996,39:3553.
[12] 赵崇斌,张楚汉.映射动力无穷元及其特性研究[J].地震工程与工程动,1987,3(22):1.ZHAO Congbin,ZHANG Chuhan.Studies on the characteristics of dynamic mapping infinite elements [J].Journal of Earthquake Engineering and Engineering Vibration,1987,3(22):1.
[13] 张楚汉,赵崇斌.复杂地基中波动问题的数值模拟[J].土木工程学报,1987,20(4):83.ZHANG Chuhan,ZHANG Congbin.A numerical simulation of wave propagation for complex foundation [J].China Civil Engineering Journal,1987,20(4):83.
[14] Eason G.The stresses produced in a semi-infinite solid by a moving surface force[J].International Journal of Engineering Science,1965,2:581.

