网络化控制多目标无功优化的进化算法
彭可,盘清琳,李仲阳,兰浩
(湖南师范大学 工学院,湖南 长沙,410081)
网络化控制无功优化系统是将网络化控制技术引入电力无功优化所形成的实时控制系统。无功优化(Reactive power optimization, RPO)是电力系统的一个经典问题[1],引入网络化控制后,能够极大地缩短无功优化的控制周期,保证电网无功的实时优化调节,从而实现电力系统的经济和安全运行。在前期研究中,笔者探讨了基于网络化控制模型和遗传算法结合的单目标无功优化控制方法,并取得了一定研究结果[2]。一些研究者也提出将网络化控制应用于电力系统实时监控[3],或是致力于研究各种无功优化算法的性能对比及改进方法[4-5]。但是,同时针对网络化控制传输模式和多目标优化算法改进的研究很少。网络化控制利用通信网络传输的实时电网状态来进行无功的优化调节,必须分析和解决网络传输模式及其带来时滞或丢包等影响;而多目标优化是对于多个相互制约性能指标的综合寻优,有必要探讨并行的全局搜索机制以便能较快得到最优解。差分进化算法(Differential evolution, DE)是一种启式优化算法,具有原理简单、受控参数少、对优化问题特性不敏感等优点。为此,本文作者研究一种网络化控制多目标无功优化的改进进化算法。它主要基于改进DE算法,利用双群体搜索机制进行寻优,使得算法能有效地应对带约束条件的多目标无功优化[6-7];同时,针对网络化控制中时间驱动数据传输模式对优化算法的影响,采用去冗-保持处理以解决网络丢包问题[2]。针对IEEE30系统进行仿真实验,验证该算法的可行性和有效性。
1 网络化控制多目标无功优化的建模
1.1 网络化控制无功优化中节点的数据传输模式
网络化控制无功优化本质上是一种网络化控制系统(Networked control system, NCS),数据丢包是必须解决的问题。除了网络拥塞和连接中断等常见的丢包原因外,节点的数据传输模式也会造成数据丢包。在网络化控制系统中,节点数据的基本传输模式通常有2种:时间驱动和事件驱动。时间驱动的数据传输模式是:在系统时钟作用下,控制器节点定时从传感器节点接收状态信息,在控制器端进行计算处理;同时,执行器节点也从控制器节点接收控制指令,完成相应的输出操作。事件驱动的数据传输模式为:控制器节点或执行器节点只有在分别接收到对应的状态信息或控制指令后,才进行下一步数据计算或控制输出。2种节点传输模式的时序分析结果分别如图 1和图 2所示。
从图1和图2可以看出:采用事件驱动方式传输数据时,接收节点只在收到发送节点的状态数据或控制指令后,才会进行相应的控制计算或输出处理;整个控制过程的时序流程由接收数据事件来驱动,其控制运算和输出动作的时间具有不确定性,严格来说为非周期性控制。而采用时间驱动方式传输时,只要到达预定周期,传感器节点就会自动采样,控制器节点自动计算,执行器节点自动输出控制操作,其控制过程为周期性控制。在具有全局时钟的情况下,网络化控制无功优化系统一般应采用时间驱动传输模式,以保证其优化调节性能的稳定。本文主要探讨时间驱动方式下的多目标无功优化。
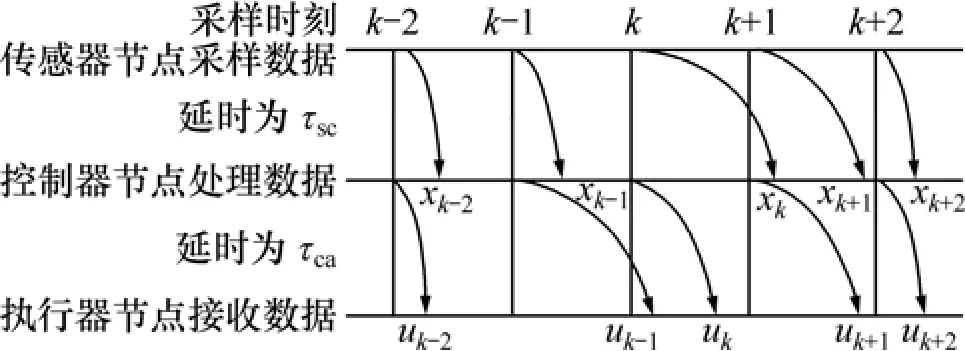
图1 网络化控制无功优化中节点的时间驱动传输Fig.1 Time-driving transmission chart of nodes in network-controlled RPO
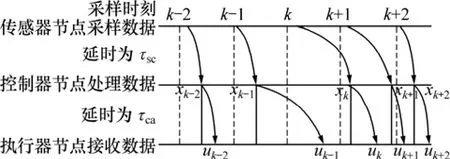
图2 网络化控制无功优化中节点的事件驱动传输Fig.2 Event-driving transmission chart of nodes in network-controlled RPO
在时间驱动传输模式中,接收节点在固定周期内必然要接收1个状态或控制数据。如果在1个周期内2个或多个数据同时到达,接收节点就会选取时刻较近的数据,从而造成数据丢弃;另一方面,如果在 1个周期内没有数据传输过来,那么,相应节点就会保持前一时刻的历史值,造成空采样。这2种情况都会造成数据丢包。例如图1中,对于第k+2时刻的控制器节点和第k+1时刻的执行器节点,因为传感器信息xk与xk+1同时到达控制器,控制信号uk-1与uk同时到达执行器节点,接收节点选取较近xk+1和uk,那么,传感器信息xk和控制信号uk-1发生了丢弃现象;而第k+1时刻的控制器节点和第k时刻的执行器节点因为没有新数据到达,相应节点就会保持前一时刻的历史值xk-1和uk-2,导致出现空采样现象。
1.2 网络化控制无功优化系统的多目标优化模型
网络化控制多目标无功优化是:无功优化系统引入网络化控制模式,并选取2个或2个以上函数作为优化目标[8-10]。本文以选取有功网损最小、电压稳定性最好(电压下降最小)为例,共同作为目标函数,建立该系统的优化模型如下:

式中:FL为系统的有功网损;FV为电压下降偏移量;等式约束为潮流平衡约束,即各节点有功和无功的平衡方程;不等式约束包括电容器无功补偿容量、有载变压器档位、发电机电压等控制变量约束(用u表示),以及发电机无功功率、PQ节点电压等状态变量约束(以x表示)以及网络传输时延约束(τsc为传感器节点到控制器节点的传输延迟变量,τca为控制器节点到执行器节点的传输延迟变量,τscmax和τcamax,τscmin和τcamin分别为其上、下限)。若网络传输时延τsc>τscmax或τca>τcamax,则发生了数据丢包[2-3]。
2 时间驱动下数据丢包的处理与算法改进
2.1 时间驱动模式下的数据丢包及处理
如上所述,时间驱动模式下数据丢包的2种形式为数据丢弃和空采样。在单周期控制的方式下,两者均可视为τ>T(其中,T为系统中各传感节点或控制节点的控制周期,τ为传输时延)。在网络化控制无功优化系统中,数据丢包对于优化算法的影响很大[11-13]。针对系统中数据丢包的情况(包括前向通道与反馈回路),提出采用“去冗-保持”处理方法来解决[2]。所谓去冗-保持是指:在控制器进行优化计算时,去掉那些没有必要参与寻优迭代的不可测状态量或不可控的控制量,以达到简化寻优计算目的;而在执行器端,保持不可控输出量的历史值,以保证网络化控制无功优化系统能够得到次优解,并减少数据丢包对优化运算量的影响。
具体实现方法是:在控制器端引入网络状态对角阵S,用于存放系统中控制量u和状态量x的网络传输状态;在S中,值为“0”表示对应的控制量暂不可控或状态量暂不可测(即网络出现数据丢包情况),值为“1”则表示该控制量可控或状态量可测;通过当前的网络通讯状态来自动设置S中控制量或状态量的对应值。在无功优化迭代求解过程中,首先应将控制变量u和状态变量x共同构成广义状态向量x′,将该向量x′与对角阵S相乘,从而将相应的不可测分量xbc和不可控分量ubk剔除出迭代优化计算;然后,当可控分量ukk迭代产生了新的优化值后,采用xbc和ubk保持的前一次历史值,与可测分量xkc和可控分量ukk一起参与优化目标函数和约束条件的验证;最终控制器实际输出量u将由验证过的最优可控分量ukk与不可控分量ubk历史值而共同构成。该方法的计算步骤如下。
(1)构成广义状态向量:

广义状态向量x′的维数为 1×m,且m=p+n;其中,p为系统状态变量个数,n为控制变量个数。
(2)引入网络状态对角阵S:
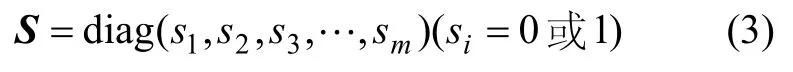
其中:i∈[1,m],指明状态量或控制量位于网络状态对角阵S中的位置。
(3)去冗操作。
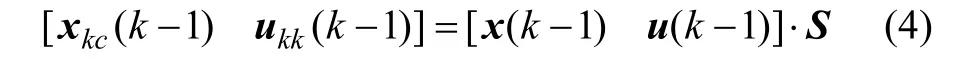
式(4)中,通过网络状态对角阵S,将不可控输出量和不可测状态量从广义状态向量x′中作为冗余量归零化处理,以保留可控输出量和可测状态量。针对不同的优化算法,去冗操作的归零化不能仅理解为矩阵乘法运算;对于非线性变换的优化方法,去冗操作可依据具体情况而不同。
(4)优化迭代计算。
仅对于广义状态向量x′中可控分量ukk、可测分量进行迭代寻优计算,不可控分量ubk和不可测分量归零后不参与寻优迭代。按照原有的优化迭代方法,由(k-1)经过迭代运算得到新的优化值ukk(k)。
(5)保持操作。
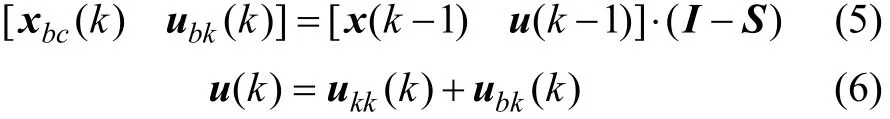
式中:I为单位对角阵,从而将不可控分量ubk和不可测分量xbc保持为前一时刻历史值,再通过式(6)与由优化迭代产生的可控分量ukk(k)共同形成控制器的最终控制量u(k);并应把广义状态向量x′(k)代入式(1)进行目标函数和约束条件的验证计算。
2.2 具有数据丢包的多目标无功优化改进DE算法
从式(1)可知:网络化控制多目标无功优化的实质是一类带约束条件的多目标优化问题。通过容许误差(也称容忍度)方法能够将等式约束转化为不等式约束,该问题可采用文献[6]和[7]中的改进DE算法予以解决。基本思路如下。
由于带约束优化问题的最优解可能位于可行域和不可行域的边界上或附近,甚至不可行域中不可行解优于可行域中大部分可行解,为了提高全局寻优速度和性能,需综合考虑多目标函数和约束条件。因此,应先根据约束条件来选择初始种群;再按照解的可行性将个体分为可行和不可行种群,并以不同比例分别从这2个种群中选取父代个体进行变异和交叉;接着,进行新个体的可行性判定,并将它们分别存放;最后,基于Pareto分类排序完成对新个体的选择操作[14],保留下一代优秀个体,从而确定新的可行和不可行种群。同时,该算法还针对初始种群结合Logistic 映射来混沌初始化;对于变异操作引入最优可行解gbest和缩放因子F的模拟退火策略,并综合考虑可行与不可行解集的优良性能,以改进变异操作方程;在交叉操作中,交叉算子CR也利用模拟退火因子来提高后期局部寻优能力;对新可行种群的选择操作采用目标函数的Pareto最优,而对新不可行种群的选择操作操作采用约束向量的Pareto最优。
该改进DE算法的具体实现步骤如下。
(1)初始化操作。取全部种群规模为N,且N=N1+N2(N1为可行种群规模,N2为不可行种群规模);采用Logistic 映射混沌初始化每一个个体xi,判断其可行性,分别归入可行种群和不可行种群中待用,并统计出可行个体数目NF和不可行个体数目NI。
(2)变异操作。在双群体进化策略中,为了保持群体的多样性和收敛性,充分利用已搜索到的可行群体和不可行群体,取变异操作方程为:
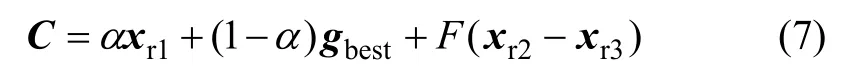
其中:xr1为可行种群中的随机个体;xr2和xr3为整个群体中的随机个体;退火因子α=(T-t)/T;T为最大迭代数;t为当前迭代数;缩放因子F=Fmin+α(Fmax-Fmin)。
因此,当α由1逐渐变化为0时,xr1,gbest和F等参数能够进行自适应调整;算法开始时,全局搜索能力强,而后期局部搜索能力增强。
(3)交叉操作。变异产生的个体C=(c1,c2,…,)与父代个体X=(x1,x2,…,xm)通过如下交叉操作,得到新个体
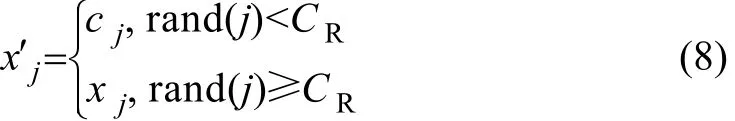
其中:j∈ [1 ,m];m为个体的分量个数;随机函数rand(j)∈ [ 0,1]。交叉过程中也引入了模拟退火策略,取交叉算子CR为:
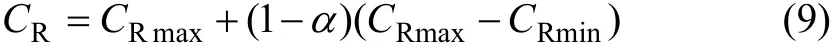
当α由1逐渐变化为0时,前期CR较小,便于保留良好基因;后期CR增大,加快了收敛速度。式(9)中,CRmax、CRmin分别为CR的最大与最小值。
(4)判断新个体的可行性。通过变异和交叉产生新个体X′后,需判断其可行性;并统计产生的新可行个体数目M1和新不可行个体数目M2。
(5)选择操作。采用双群体搜索机制,基于Pareto分类排序多目标优化而进行选择操作。
新可行种群的确定:若NF+M1≤N1,则保留全部可行解作为下一代可行种群;否则,选取目标函数向量Pareto较优的前N1个可行解,构成新的可行种群。可行解集中各个体对应的目标向量若存在2个目标向量Pareto可比,则保留目标向量较优的个体;若无可比个体,则计算各个体间的距离,并随机剔除距离最小2个个体中的1个,直至选出N1个个体的新一代可行种群为止。
新不可行群的确定:若NI+M2≤N2,则保留全部不可行解作为下一代不可行种群;否则,选取约束向量Pareto较优的前N2个不可行解,构成新的不可行种群。不可行解集中各个体对应的约束向量,若存在 2个约束向量Pareto可比,则保留约束向量Pareto较优的个体;若无可比个体,则剔除全部不可行解中约束度最大的个体,直至选出N2个个体的新一代不可行种群为止。
网络化控制多目标无功优化的改进DE算法具体流程如图3所示。
3 算例与分析
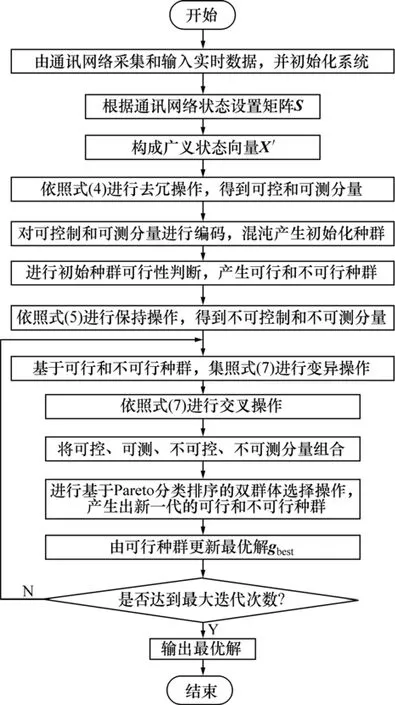
图3 本文算法的整体流程图Fig.3 General flowchart of the proposed algorithm
为了验证本文改进DE算法处理多目标无功优化问题的可行性以及所提去冗-保持处理方法针对网络丢包的有效性,采用IEEE30节点系统进行仿真实验。该系统具有12个控制变量,包括6个发电机节点、4台变压器和2个无功补偿节点。节点电压上、下限分别为1.10和0.95,变压器变比上、下限为1.10和0.90,系统初始状态的有功网损值为 17.557 MW,压降为6.23。在仿真实验过程中,进化计算的代数设置为200,种群规模设置为50[14-15]。
首先假设系统中控制变量均可控、状态变量均可测,分别采用基本DE算法、遗传算法和本文双群体改进DE算法进行多目标无功优化的计算。这3种算法的网损和压降收敛曲线如图4所示。将这3种算法各运行10次,并选出较优的计算结果进行对比,结果如表1所示。从图4可知:改进DE算法计算到133代已基本收敛到最优解,而基本DE算法和GA算法则分别需计算到155代和148代才能基本收敛;并且改进DE算法的收敛曲线相比于后两者更平滑,优化效果也更优。从表1可知:与初始状态相比,采用基本DE算法进行优化计算,有功网损降低6.21%,电压降下降 85.88%;采用 GA算法计算,网损降低5.58%,电压降下降85.25%;而采用本文改进DE算法计算,网损则降低7.21%,电压降下降87.69%。经综合对比后发现:改进DE算法有功网损和压降均低于基本DE算法和GA算法。因此,采用改进后的双群体DE算法处理多目标无功优化问题,能够在优化性能、收敛速度和结果均匀性上均优于上述传统算法。
为了进一步分析去冗-保持处理方法对于数据丢包问题的有效性,设定 IEEE30系统存在不可控变量数目N及不可测变量数目C分别为如下4种情况:(a)N=3,C=0;(b)N=3,C=1;(c)N=5,C=0;(d)N=5,C=1;且结合本文改进 DE算法分别针对无数据丢包理想系统、未采用去冗-保持处理系统、采用去冗-保持处理系统的网损分别进行仿真计算,结果如图 5所示。仿真结果表明:
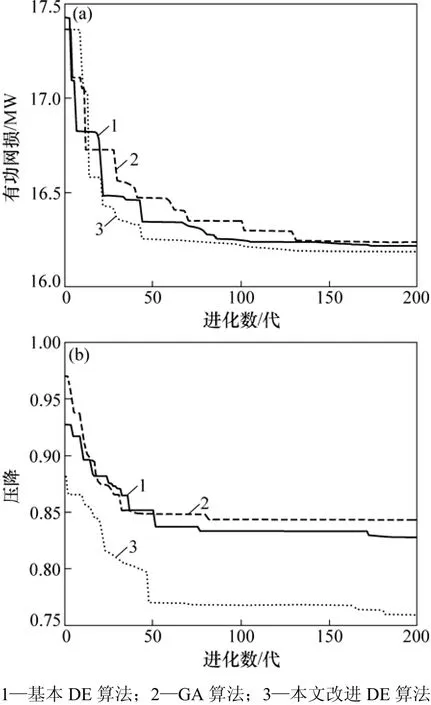
图4 基本DE算法、GA算法和改进DE算法的网损及压降收敛曲线Fig.4 Loss and voltage drop convergence curves of basic DE, GA and improved DE algorithms
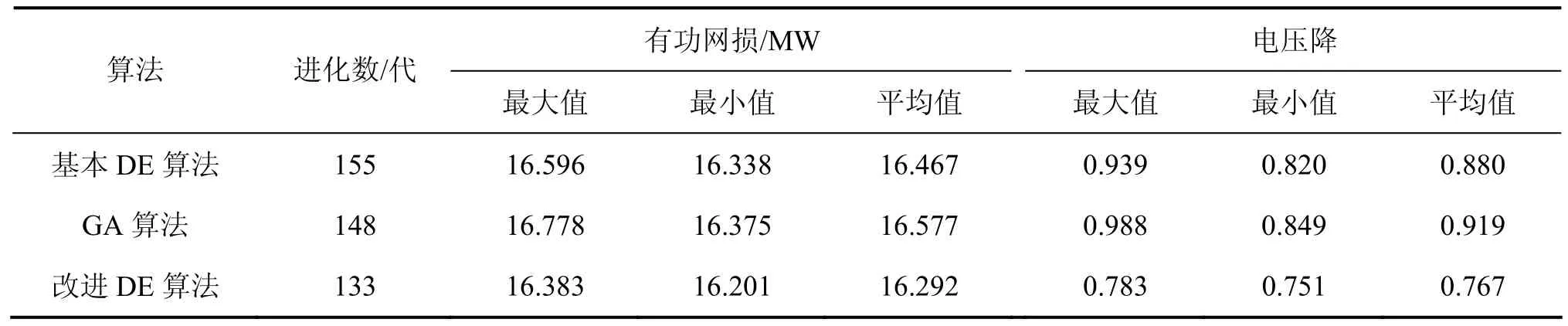
表1 基本DE算法、GA算法与本文改进DE算法的10次计算结果比较Table 1 Comparison of ten times calculation results obtained by basic DE ,GA and improved DE algorithm
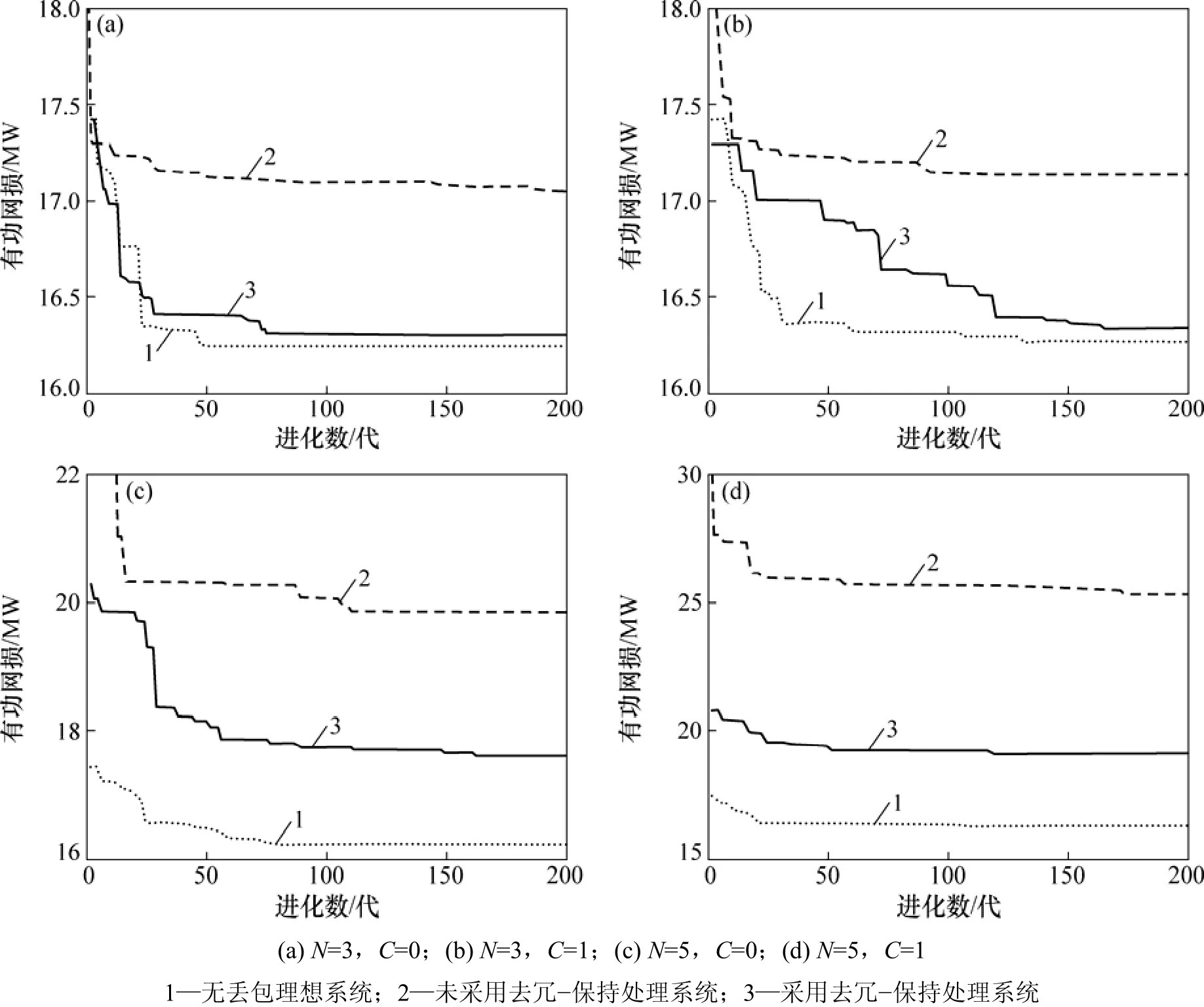
图5 无丢包、未采用及采用去冗-保持处理系统的网损收敛曲线Fig.5 Loss convergence curves of ideal, without and with redundancy-removal and maintaining process systems
(1)网络化控制无功优化系统在时间驱动传输模式下造成的数据丢包会引起控制量不可控或状态量不可测,从而影响系统的优化性能。其中,不可测状态量对系统的影响更大。若不进行改进,相应的优化计算结果与理想系统的优化计算结果相差甚远,系统优化性能明显降低。
(2)采用本文中去冗-保持处理方法可以解决不可控或不可测量引起的系统性能下降问题,使得最终优化结果与理想系统的计算结果更为逼近。但是,随着不可控或不可测变量数目增多,无论算法改进与否,系统均难以达到理想状态。
4 结论
(1)针对时间驱动模式下具有数据丢包的网络化控制多目标无功优化问题,提出先将等式约束转化为不等式约束,再通过双群体搜索机制,基于Pareto分类排序的改进DE算法进行处理,该算法的均匀性和收敛速度有较大提高。
(2)对于由数据丢包引起的不可控输出量或不可测状态量降低了系统优化性能的问题,引入去冗-保持处理方法,使得优化结果更接近理想系统,提高了算法的逼近性。该改进算法不仅能较好地处理带约束的多目标无功优化问题,而且能有效克服网络传输带来的数据丢包的影响。
[1]陈功贵, 李智欢, 孙永发, 等. 电力系统无功优化 LRS-PSO算法[J]. 电力系统及其自动化学报, 2008, 20(4): 92-97.CHEN Gong-gui, LI Zhi-huan, SUN Yong-fa, et al. LRS-PSO algorithm for optimal reactive power[J]. Electric Power System and its Automation, 2008, 20(4): 92-97.
[2]彭可, 黄丹, 罗安. 基于网络化控制模型的改进无功优化算法[J]. 电网技术, 2011, 35(3):103-107.PENG Ke, HUANG Dan, LUO An. An improved reactive power optimization algorithm based on networked control model[J].Power System Technology, 2011, 35(3): 103-107.
[3]何飞跃. 网络化控制系统在电力系统中的应用研究[D]. 武汉:华中理工大学电气与电子工程学院, 2006: 20-23.HE Fei-yue. Application of Networked Control System in Power System[D]. Wuhan: East China University of Science and Technology. College of Electrical and Electronics Engineering,2006: 20-23.
[4]赵树本, 张伏生. 基于改进差分进化算法的电力系统最优潮流计算[J]. 电网技术, 2010, 34(8): 123-128.ZHAO Shu-ben, ZHANG Fu-sheng. Solution of optimal power flow based on differential evolution and its modified algorithm[J]. Power System Technology, 2010, 34(8): 123-128.
[5]梁才浩, 钟志勇, 黄杰波, 等. 一种改进的进化规划方法及其在电力系统无功优化中的应用[J]. 电网技术, 2006, 30(4):16-20.LIANG Cai-hao, Chung Y, Wong K P, et al. An improved evolutionary programming method and its application in power system reactive power optimization[J]. Power System Technology, 2006, 30(4): 16-20.
[6]孟红云, 张小华, 刘三阳. 用于约束多目标优化问题的双群体差分进化算法[J]. 计算机学报, 2008, 31(2): 228-235.MENG Hong-yun, ZHANG Xiao-hua, LIU San-yang. A differential evolution based on double populations for constrained multi-objective optimization problem[J]. Chinese Journal of Computers, 2008, 31(2): 228-235.
[7]俞国燕, 李鹏, 何真, 等. 一种用于多目标约束优化的改进进化算法[J]. 计算机集成制造系统, 2009, 15(6): 1172--1178.YU Guo-yan, LI Peng, HE Zhen, et al. Advanced evolutionary algorithm used in multi-objective constrained optimization problem[J]. Computer Integrated Manufacturing Systems, 2009,15(6): 1172-1178.
[8]肖晓伟, 肖迪, 林锦国, 等. 多目标优化问题的研究概述[J].计算机应用研究, 2011, 28(3): 805-808, 827.XIAO Xiao-wei, XIAO Di, LIN Jin-guo, et al. Overview on multi-objective optimization problem research[J]. Application Research of Computers, 2011, 28(3): 805-808, 827.
[9]张武军, 叶剑锋, 粱伟杰, 等. 基于改进遗传算法的多目标无功优化[J]. 电网技术, 2004, 28(11): 67-71.ZHANG Wu-jun, YE Jian-feng, LIANG Wei-jie, et al.Multiple-objective reactive power optimization based on improved genetic algorithm[J]. Power System Technology, 2004,28(11): 67-71.
[10]彭可, 吴思聪, 肖建宏, 等. 无源电力滤波器参数的混沌模拟退火优化设计[J]. 电力自动化设备, 2009, 29(8): 55-58.PENG Ke, WU Si-cong, XIAO Jian-hong, et al. Passive power filter parameter optimization based on chaos and annealing strategy[J]. Electric Power Automation Equipment, 2009, 29(8):55-58.
[11]邱占芝, 张庆灵, 刘明. 有时延和数据包丢失的网络控制系统控制器设计[J]. 控制与决策, 2006, 21(6): 625-630, 635.QIU Zhan-zhi, ZHANG Qing-ling, LIU Ming. Controller design for networked control systems with time-delay and data packet dropout[J]. Control and Decision, 2006, 21(6): 625-630, 635.
[12]张玉泉, 钟秋海, 王林. 具有时滞和丢包的网络化控制系统稳定性分析[J]. 北京理工大学学报, 2008, 28(4): 329-333.ZHANG Yu-quan, ZHONG Qiu-hai, WANG Lin. Stability of networked control systems with time delays and data-packet losses[J]. Transactions of Beijing Institute of Technology, 2008,28(4): 329-333.
[13]陈青, 吴敏. 具有网络丢包和时延的网络控制系统设计[J].控制与决策, 2011, 26(2): 293-296.CHEN Qing, WU Min. Design of networked controller for systems with packet dropout and networked-induced delays[J].Control and Decision, 2011, 26(2): 293-296.
[14]冯士刚, 艾芊. 基于强度 Pareto进化算法的多目标无功优化[J]. 高电压技术, 2007, 33(9): 115-119.FENG Shi-gang, AI Qian. Multi-objective reactive power optimization using SPEA2[J]. High Voltage Engineering, 2007,33(9):115-119.
[15]Arya L D, Choube S C, Kothari D P. Reactive power optimization using static voltage stability index[J]. Electric Power Components and Systems, 2001, 29(7): 615-628.

