无底柱分段崩落法结构参数研究

吴爱祥，武力聪, ，刘晓辉，孙希文，周颖，尹升华

(1. 北京科技大学 土木与环境工程学院，北京，100083；2. 有色金属矿产地质调查中心，北京，100012；3. 北京大地盛业房地产土地评估有限公司，北京，100013)

采矿方法结构参数不仅直接影响到开拓、采准以及回采准备的工程量，而且相应影响到投资、成本和采矿效益等。此外，对于像无底柱分段崩落法这类采矿方法，一般认为，结构参数还直接影响到矿石回收指标和回收效果，从而全面影响到矿山开采的技术经济指标和效益[1]。正因为如此，采矿方法结构参数历来受到生产矿山、科研以及设计等方面的高度重视。无底柱分段崩落法的结构参数除要取得较高的矿石回收率外，还要充分发挥凿岩和出矿设备的生产能力，降低开采成本，提高采矿效率。根据放矿模拟实验的结果，结构参数有2种趋势：一种是分段高度大于进路间距的高分段结构形式，另一种是分段高度小于进路间距的大间距结构形式。这2种结构形式都具有节约采准工程量、一次崩矿量大、采矿强度大等优点，但在具体操作过程中有很大的区别，大间距结构形式因其可操作性更强、凿岩费用更低和采场地压管理更简单等优点[2-3]而备受关注。本文作者以湖北某铁矿为例，通过室内放矿试验和计算机数值模拟两种方法，以大间距结构参数理论为基础，对该铁矿采矿方法结构参数进行研究分析，并最终确定最合理的采矿方法结构参数。

1 大间距结构参数理论

大间距空间排列理论跳出单个放出体[4]的框架，着重研究各放出体之间空间排列问题，而所用的基本原则没有变，还是采用崩落矿石的爆破堆积体形态应尽可能地与放出体形态相吻合。

大间距结构形式[5-6]如图1所示，上下2个球体相切，左右两个球体被分开，且分别与上下2个球体相切，设椭球体长轴半径为a，短轴半径为c，则按椭球体布置进路时，分段高度为：

进路间距为：

图1 大间距放出椭球体排列形式Fig.1 Large space drawing ellipsoid arrange form

显然，

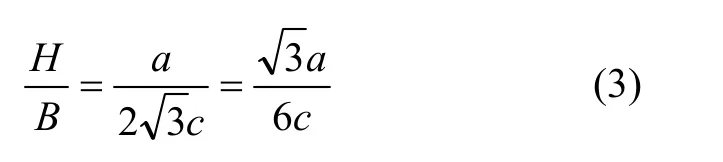
2 研究方案

正交实验法[7]就是利用排列整齐的表——正交表来对试验进行整体设计、综合比较、统计分析，实现通过少数的实验次数找到较好的生产条件，以达到最高生产工艺效果。由于正交试验能以较少的试验次数获得较多的信息量，试验点安排的均匀而具有代表性，试验所得结果可靠且能说明问题。因此，采用正交试验法对结构参数进行分析。

从放矿角度考虑，影响无底柱分段崩落法矿石回收指标的参数因素包括分段高度(H)、进路间距(B)、放矿步距(L)、边孔角(α)、进路尺寸(a×b)、崩落矿岩块度、出矿铲取方式、铲取深度以及炮孔排面倾角等，但其中最主要的3个因素还是分段高度、进路间距和崩矿步距。本次实验就是选取分段高度、进路间距和崩矿步距3个因素，对放矿过程进行模拟，以求获得可以指导实际的最优结构参数。基于此，将影响矿石回收的主要因素分段高度、进路间距和崩矿步距作为正交试验的3个代表因素。

综合考虑目前矿山的技术装备水平、管理水平以及现有实验室条件，拟定的因子水平为3个水平，具体的因素确定情况见表1。

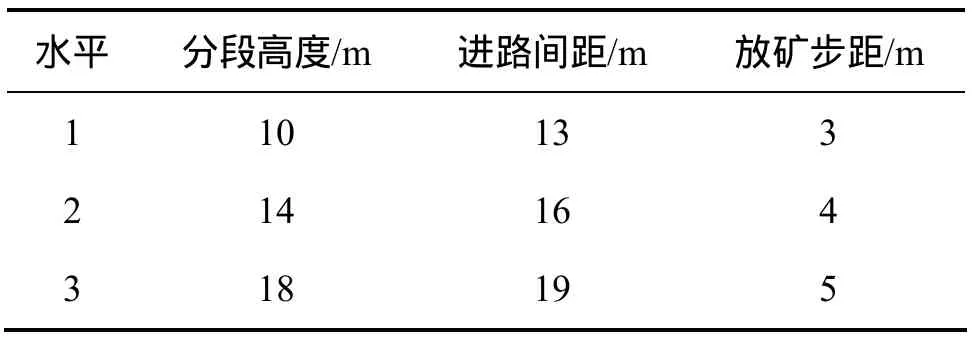
表1 正交试验因素水平表Table 1 Orthogonal Experiment factor level

3 室内放矿试验研究

3.1 试验模型

本次研究，主要是利用多分段立体放矿模型[8]在实验室进行放矿试验。由于本次试验根据参数选取不一样共有9种放矿方案，因此，放矿模型也与参数对应的有9个。模型的相似比为1:100，共有2个分段，每个分段有5～6条回采进路，每条进路有4个步距；采矿方法的主要结构参数(H×B×L)为14 m×16 m×5 m，进路尺寸(高度×宽度)为3 m×3 m。

3.2 试验准备

按照1:1 000的相似比将所取回的矿石和岩石破碎为实验所需块度。根据现场要求，矿石块度定为5～8 mm，岩石块度定为 8～20 mm。为方便观察矿石和岩石分界线运动规律，特利用油漆将岩石染为鲜红色，以与黑色的矿石形成鲜明的对比。

3.3 试验结果

根据正交试验的因素水平，选用 L9(34)正交表安排本次模拟放矿试验。共计安排了9个放矿方案，每个方案只进行1个分段、1个步距放矿，但安排多个进路同时出矿。每次放矿都采用低贫化放矿方法进行出矿，即当矿石和岩石的质量比分别为2:1时，停止放矿。上分段放矿结束图见图 2，下分段放矿结束图见图 3。三因素三水平正交试验表及其模拟放矿指标见表2。

3.4 结果分析

正交试验法中，各影响因素对结果的影响程度可用极差R来确定[9]。极差R越大，表明该因素对结果的影响也大，反之就小。通过对表2中矿石回收率极差R的比较，可以发现，影响矿石回收率的3个主要因素中，分段高度对矿石回收率的影响最大，进路间距其次，影响最小的是放矿步距。

图2 第一分段放矿结束图Fig.2 Ore drawing final chart of first section

图3 第二分段放矿结束图Fig.3 Ore drawing final chart of second section

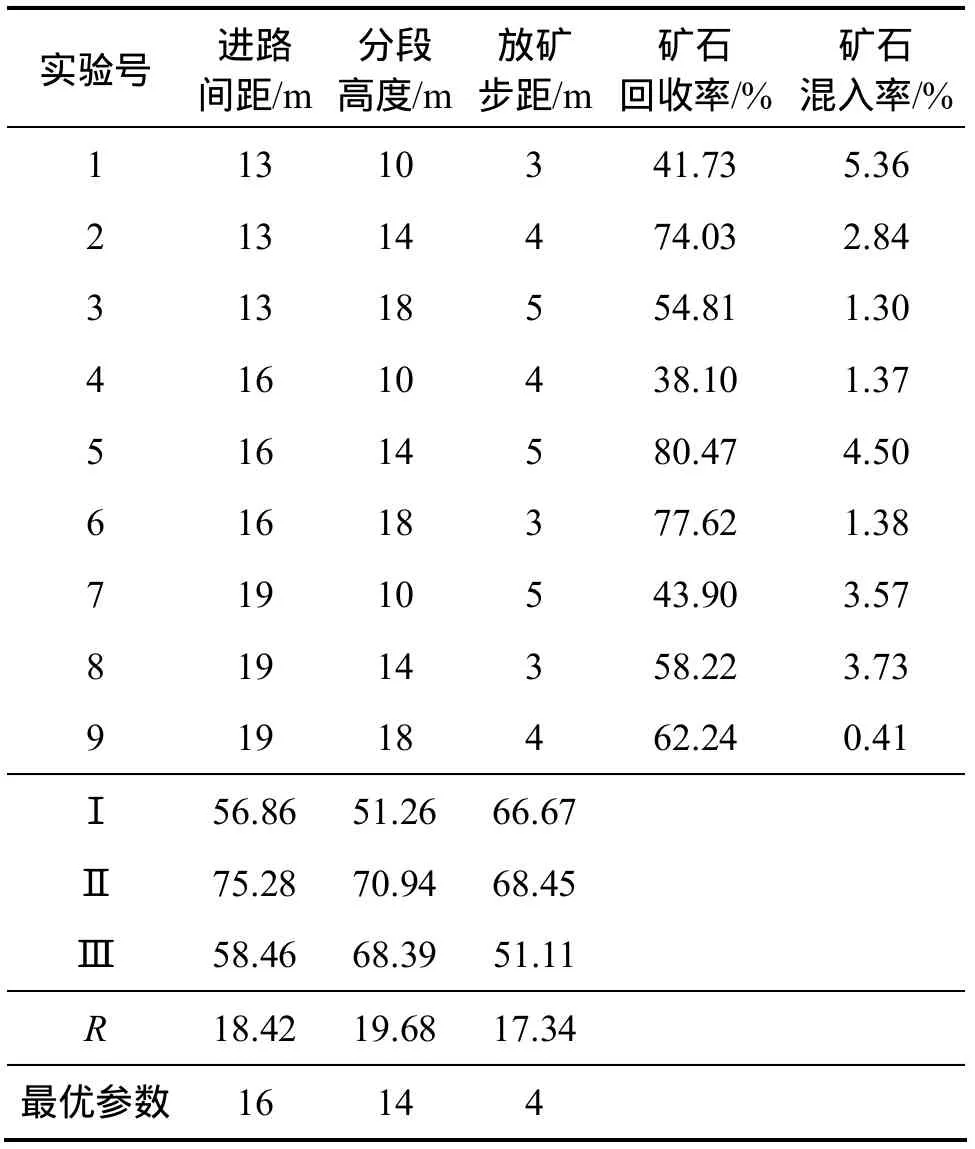
表2 三因素三水平正交试验表及放矿指标表Table 2 Three factors and levels orthogonal experiment and ore drawing index

极差分析可以定量地确定3个主要因素对矿石回收率影响的敏感程度，但不能看出矿石回收率随各因素变化的变化趋势，以各因素为横坐标，以矿石回收率指标为纵坐标，绘制出因素与指标的趋势图，如图4所示。

由图4可以发现：不论分段高度和放矿步距，还是进路间距，矿石回收率的变化趋势都是随它们高度的增大而呈现先变大后减小的趋势。这表明矿石回收率必定在该选定参数水平之间必有1个峰值，而且是最大值。因此，可以将该铁矿的采场结构参数定为：进路间距16 m，分段高度14 m，放矿步距4 m。

4 数值模拟研究

4.1 三维放矿模型参数确定

PFC3D软件是通过细观力学参数表征颗粒及黏结的力学性质[10-11]。对数值模型进行计算分析之前，必须赋予模型假定的细观力学参数，进行数值试样试验，并将计算得到的试样宏观力学参数与室内试验结果对比，不断调整细观力学参数，当计算结果与试验结果一致时，便可将该组细观力学参数应用于实际计算模型。

图4 矿石回收率趋势图Fig.4 Trend of ore recovery ratio

本文采用的三维放矿数值模型尺寸与室内试验保持一致，颗粒相互接触模型采用接触-刚度模型。该模型建模参数主要包括矿石与岩石颗粒半径、法向刚度、切向刚度、摩擦因数、密度和颜色等，通过反复调试，当采用表3中的细观力学参数时，基本与宏观力学参数相吻合。

4.2 数值模拟

与室内试验对应，放矿数值模拟也有9个不同的模型，本文仅以其中一组放矿参数建立放矿模型为例进行分析[12-13]。首先定义墙体，其尺寸与室内试验参数一致，并在该墙体控制区域内随机生成颗粒，颗粒半径采用高斯分布。为提高颗粒的生成速度与计算效率，先生成小直径的颗粒，在利用膨胀系数扩大半径，并通过膨胀生成初始应力场，最后通过循环来消除模型内部的非均匀应力。图5所示为放矿过程图。

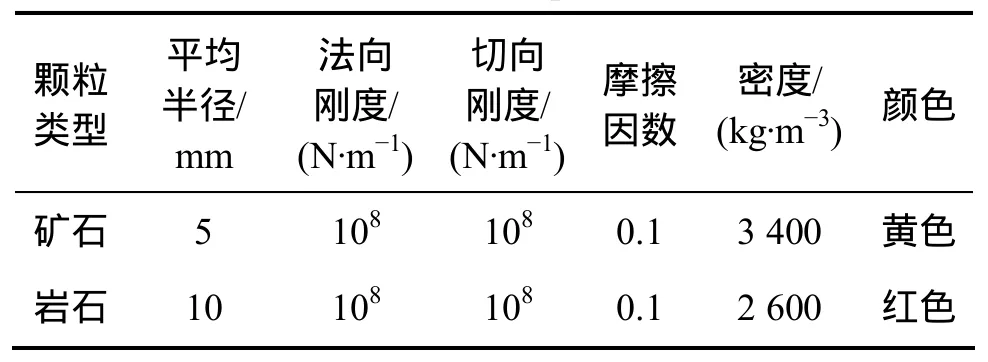
表3 颗粒参数表Table 3 Particle parameters

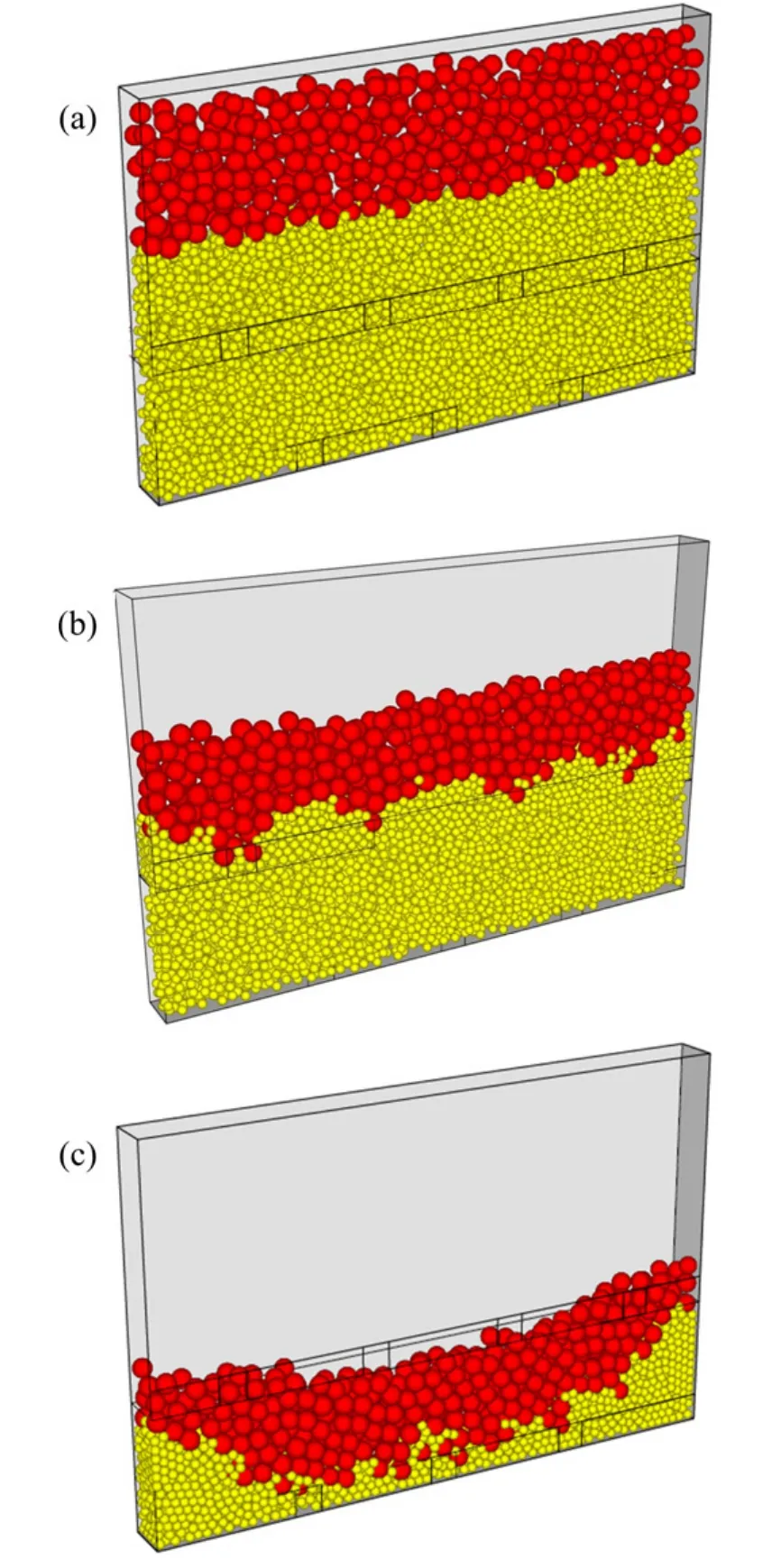
图5 放矿过程图Fig.5 Ore drawing process

4.3 模拟结果

根据计算机放矿过程，分别统计最后的矿石回收率与岩石混入率可得到以下结果。与室内试验一致，由于首分段要保留微贫化层，并且脊部残留较大，因此，结果统计以第二分段放矿数据为准。数值模拟放矿数据表见表4。

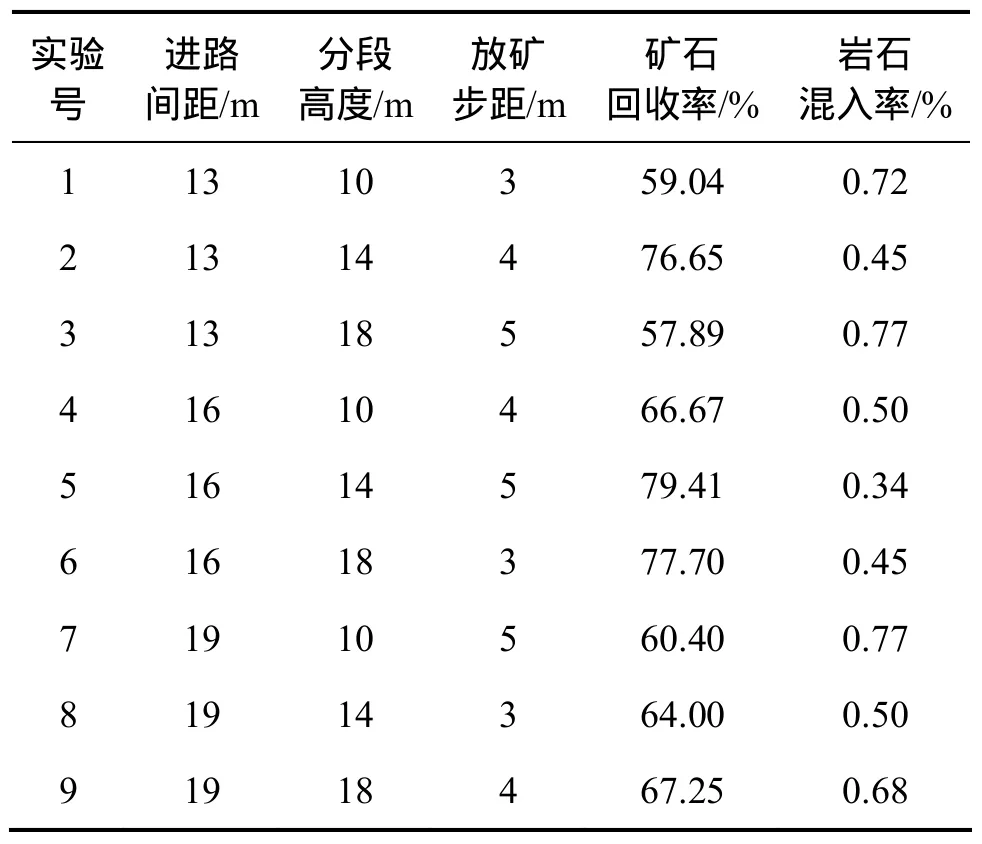
表4 数值模拟放矿数据表Table 4 Numerical simulation ore drawing data

4.4 结果分析

根据计算机模拟出的各个放矿方案的放矿结果，建立1个只考虑分段高度、进路间距和放矿步距三大因素的矿石回收率的回归方程[14-15]。利用Matlab计算出各项回归系数，可直接写出无底柱分段崩落法的矿石回收率回归方程为：

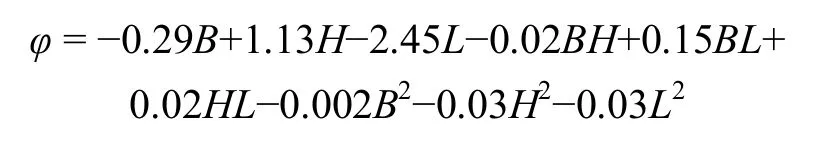
该回归方程可用于预估各种参数条件的矿石回收指标并对各参数方案进行定量分析和评价，也可以在更广泛的范围内说明矿石回收率与分段高度、进路间距和放矿步距等三大影响因素的变化关系。固定回归方程中的某些因素并将回归方程进行简化，就可以得到不同参数对矿石回收率的影响情况如图6所示。

综合以上回归分析的结果，并结合大间距结构参数理论可以发现：

(1) 在放矿步距、分段高度以及进路间距三大影响因素中任意2项因素一定后，另一因素对矿石回收率的影响均呈现二次曲线的变化关系，且都是呈先增大再减小的变化趋势。

图6 矿石回收率与影响因素关系图Fig.6 Relationship between ore recovery ratio and influence factor

(2) 放矿步距、分段高度以及进路间距3个参数在拟定的水平因子区间都存在1个使矿石回收率达到最大的水平因子。

(3) 根据图 6可以发现：当放矿步距、分段高度和进路间距分别定为4，14和16 m时，矿石回收率可以达到最大值。

5 结论

(1) 放出体基本为椭球体，这完全符合放矿椭球体理论，即放矿过程满足椭球体理论。这表明本研究可以保证理论上的合理性。

(2) 进路间距、分段高度、放矿步距这 3个主要因素对矿石回收率的影响各不一样。其中，分段高度对矿石回收率的影响最大，进路间距其次，影响最小的是放矿步距。

(3) 将该铁矿采场结构参数定为：分段高度14 m，进路间距16 m，放矿步距4 m。

[1]任凤玉, 韩智勇, 王文杰, 等. 北洺河铁矿采场结构参数的确定方法[J]. 中国矿业, 2006, 15(3): 44-46.REN Feng-yu, HAN Zhi-yong, WANG Wen-jie, et al. Study on the structure parameters of sublevel caving in Beiming iron mine[J]. China Mining Magazine, 2006, 15(3): 44-46.

[2]张国联, 邱景平, 宋守志, 等. 无底柱分段崩落法回收指标与分段数关系研究[J]. 金属矿山, 2004(4): 14-16, 19.ZHANG Guo-lian, QIU Jing-ping, SONG Shou-zhi, et al. Study on relationship between recovery index and sublevel number in pillarless sublevel caving[J]. Metal Mine, 2004(4): 14-16, 19.

[3]张国联, 邱景平, 宋守志, 等. 张家洼矿无底柱分段崩落法结构参数灰色决策[J]. 东北大学学报: 自然科学版, 2006, 27(4):454-457.ZHANG Guo-lian, QIU Jing-ping, SONG Shou-zhi, et al. Grey decision-making for constructional parameters of non-pillar sublevel caving in Zhangjiawa Iron Mine[J]. Journal of Northeastern University: Natural Science, 2006, 27(4): 454-457.

[4]高永涛. 放出期望体理论与电算模拟放矿的相似性[J]. 北京科技大学学报, 1994, 16(3): 201-204.GAO Yong-tao. Searching similarity of computer simulating drawing based on EVB drawing theory[J]. Journal of University of Science and Technology Beijing, 1994, 16(3): 201-204.

[5]金闯, 董振民, 范庆霞, 等. 梅山铁矿大间距结构参数研究与应用[J]. 金属矿山, 2002(2): 7-9.JIN Chuang, DONG Zhen-min, FAN Qing-xia, et al. Research and application of large space structural parameters[J]. Metal Mine, 2002(2): 7-9.

[6]董振民, 范庆霞, 金闯, 等. 大间距集中化无底柱采矿新工艺研究[J]. 金属矿山, 2004(3): 1-4.DONG Zhen-min, FAN Qing-xia, JIN Chuang, et al.Investigation of new technology of wide-spaced centralized pillar less mining[J]. Metal Mine, 2004(3): 1-4.

[7]田冬梅, 蒋仲安, 姚建, 等. 基于正交试验与回归统计方法的露天矿运输扬尘影响因素分析[J]. 北京科技大学学报, 2009,31(8): 957-963.TIAN Dong-mei, JIANG Zhong-an, YAO Jian, et al. Influencing factors analysis of dust mass concentration by transportation in open-pit mines based on orthogonal experiment and multiple regression statistics[J]. Journal of University of Science and Technology Beijing, 2009, 31(8): 957-963.

[8]程爱平, 许梦国, 刘艳章, 等. 金山店铁矿低贫化放矿试验研究[J]. 金属矿山, 2010(7): 23-25.CHENG Ai-ping, XU Meng-guo, LIU Yan-zhang, et al.Experimental study on low dilution ore drawing in Jinshandian Iron Mine[J]. Metal Mine, 2010(7): 23-25.

[9]李爱兵. 边坡稳定性影响因素敏感度的正交极差分析方法[J].勘查科学技术, 1995, 13(4): 28-31.LI Ai-bing. Orthogonal polar difference analysis method of the sensitivity of the influencing factors or slope stability[J]. Site Investigation Science and Technology, 1995, 13(4): 28-31.

[10]Itasca Consulting Group Inc. Particle flow code (Version 3.0)[M].Minneapolis: ICG, 2004: 22-26.

[11]Brady B H G, Brown E T. Rock mechanics for underground mining[M]. London: Allen & Unwin, 1985: 334-339.

[12]朱焕春. PFC及其在矿山崩落开采研究中的应用[J]. 岩石力学与工程学报, 2006, 25(9): 1927-1931.ZHU Huan-chun. PFC and application case of caving study[J].Chinese Journal of Rock Mechanics and Engineering, 2006,25(9): 1927-1931.

[13]刘志娜, 梅林芳, 宋卫东, 等. 基于PFC数值模拟的无底柱采场结构参数优化研究[J]. 矿业研究与开发, 2008, 28(1): 3-5.LIU Zhi-na, MEI Lin-fang, SONG Wei-dong, et al. Study on stope structure parameter optimization of sublevel caving without sill pillar based on numeral simulation with PFC[J].Mining Research and Development, 2008, 28(1): 3-5.

[14]邓代强, 高永涛, 吴顺川, 等. 水泥尾砂充填体劈裂拉伸破坏的能量耗散特征[J]. 北京科技大学学报, 2009, 31(2): 144-148.DENG Dai-qiang, GAO Yong-tao, WU Shun-chuan, et al.Destroy energy dissipation characteristics of cement-tailings backfill under splitting tensile condition[J]. Journal of University of Science and Technology Beijing, 2009, 31(2): 144-148.

[15]Sen S K, Shaykhian G A. Matlab tutorial for scientific and engineering computations[J]. Nonlinear Analysis Theory Methods and Applications, 2009, 71(12): e1005-e1020.