城市轨道交通站前交替折返间隔分析及计算方法
徐 意 高元生 吴 亮
徐 意:中国铁道科学研究院通信信号研究所 副研究员100081 北京
高元生:北京市轨道交通建设管理有限责任公司 工程师100037 北京
吴 亮:中国铁道科学研究院通信信号研究所 工程师 100081北京
在城市轨道交通信号系统中,列车折返间隔是限制通过能力的主要因素之一。折返间隔是否满足通过能力的需求是在项目建设前期需要重点评估的内容。折返间隔取决于具体折返站的站型、信号闭塞方式以及行车组织方式。通过详细分析采用站前交叉渡线进行站前交替折返的方式,提供计算折返间隔方法。
1 过程分析
在利用多个折返路径进行交替折返的情况下,其折返间隔将会受折返进路的交叉干扰和行车组织方式的限制。针对目前城市轨道各种站型,利用站前交叉渡线轮流以上、下行站台作为折返轨进行交替折返,能够在合理组织行车和客流的情况下有效缩短折返间隔。
如图1所示,对于不同的车辆制动性能,P0点的位置不同。对于不同的信号闭塞方式,P1、P2、P4点的位置也可能不同,可能是信号机、计轴区段的分界点或者轨道电路分界点。
具体折返过程分析:第1列车停站结束从折返站台1发出→继续运行至尾部出清P2→道岔SW1/SW4转换到反位→第3列车的进站信号开放 (目的地为折返站台1)→继续运行至尾部出清P4→道岔SW3/SW2转换到反位,同时带动道岔SW1/SW4转换到定位→出站信号开放,第2列车从折返站台2发出→继续运行至尾部出清P2→道岔SW2/SW3转换到定位→第4列车的进站信号开放(目的地为折返站台2)→第3列车出站信号开放,停站结束后从折返站台1发出。

图1 典型站前折返示意图
2 计算方法推导
以上过程周而复始地构成了站前交替折返的运行模式。从过程分析中可以得出以下结论:折返站台1的发车进路与折返站台2的接车进路为平行进路,不存在相互限制,其他到发作业之间则存在先后制约关系。制约关系体现在如图2所示站前交替折返作业时序图Ⅰ中。
图2中阶梯线表示一列车的进站、停车、出站的作业时序;虚线表示列车间到发作业的限制点,以划分前后作业的衔接关系。
根据图2,站前交替折返相关参数的计算公式推导如下。


图2 站前交替折返作业时序图I

在折返发车间隔相等的条件下,由式 (1)和 (2)得出:

由图2所示的逻辑时序限制关系,得出:

由式 (3)及 (4)得出:

根据公式 (2)、(3)、(5)就可以计算站前交替折返的折返发车间隔、折返站台1和折返站台2的停站时间。
以上是在折返发车间隔相等条件下得出的相关参数计算结果。如考虑到达间隔的限制,则有:

根据式 (5),由式 (7)得出:

正线最小追踪间隔必须小于折返站到达间隔,即:

只有验证计算结果满足式 (9),上述有关站前交替折返相关参数的计算结果才是有效的。在该条件下,通过调整折返站相邻车站的发车间隔,就可以在折返站实现预定模式的站前交替折返,从而提高折返效率,缩短折返间隔。
以下介绍不满足式 (9)的条件下,相关参数的推导过程及计算结果。
1. 如 果A_headway2<Headway≤A_headway1,则有:

由式 (10)得出:

由式 (4)及 (11)得出:
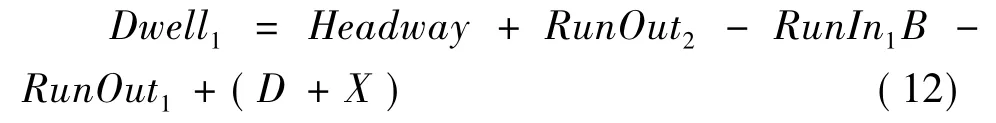
由式 (1)及 (12)得出:

在这种条件下,折返发车间隔不一定相同,根据公式 (2)、(13)、(12)、(11)就可以算出站前交替折返的交替折返发车间隔、折返站台1和折返站台2的停站时间。
2. 如 果A_headway1<Headway≤A_headway2,则需增加定义:在上一列车从折返站台2发出之后,到下一列车可以进入折返站台2之间增加空闲时间F;具体制约关系体现在图3所示站前交替折返作业时序图Ⅱ中。

图3 站前交替折返作业时序图Ⅱ
根据图3限制关系,得出:

由式 (14)得出:
根据时序限制关系,得出:

式 (3)适用于折返站台1的停站时间Dwell1的求算。
由式 (3)、(15)、(16)得出:
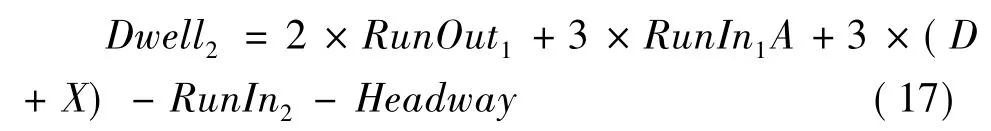
在这种条件下,根据公式 (2)、(3)、(17)就可以算出站前交替折返的折返发车间隔、折返站台1和折返站台2的停站时间。
3.如 果A_headway1<Headway, 并 且A_headway2<Headway,则有式 (11)适用于折返站台2的停站时间Dwell2的求算。
由式 (11)和 (16)得出:

由式 (1)和 (18)得出:
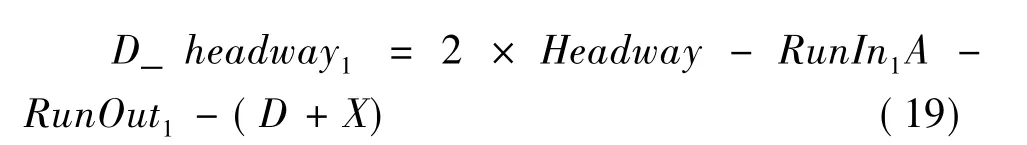
在这种条件下,折返发车间隔不一定相同,根据公式 (2)、(19)、(18)、(11)就可以算出站前交替折返的发车间隔、折返站台1和折返站台2的停站时间。
3 应用效果及结论
采用以上计算方法编制计算机程序,实现了站前交替折返间隔的快速求算。列车在折返进路中各限制点间的运行时间可根据折返进路的限速、坡度、列车的牵引制动性能,利用列车运行仿真控制模型进行计算。通过利用轨道交通实际线路数据进行站前交替折返间隔的求算,证明该计算方法行之有效,能快速准确地计算折返间隔,为评估折返能力提供了有效的方法和工具。
[1] 梁东升,徐意.CBTC列控方式下列车最小追踪间隔分析及模拟算法的实现[J].现代城市轨道交通,2011(4).

