装有软钢阻尼器钢框架地震作用下的仿真分析
闻 辉
(中冶华天工程技术有限公司,江苏南京 210019)
0 引言
对于结构在地震过程中的动力反应可以通过数值方法求解二阶微分方程来求得,实际上,对于任何一个二阶动力系统,可以将其看成一个输入—输出系统。这样可以通过MATLAB语言中的Simulink工具箱对该系统进行动态仿真。采用动态仿真计算可以避免繁杂的程序编制,同时将地震过程中的结构当作控制系统分析,概念清楚,易于理解[1]。
本文以装有软钢阻尼器的被动控制结构为例,对结构的动力反应进行动态仿真分析。
1 软钢阻尼器的等价线性化
为了便于使用Simulink工具箱对受控结构进行动力仿真,需要对软钢阻尼器非线性力进行等价线性化处理。
首先以单自由度体系为例来说明等价线性化的原则。由动力学知识可知,在地震作用下单自由度非线性结构体系的动力方程可表示为:
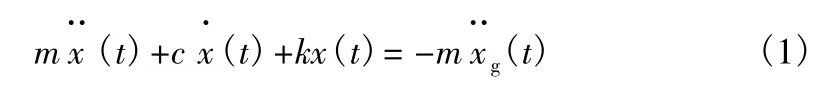
其中,m为体系的质量;x(t)分别为体系相对于地面的水平位移、速度、加速度为地面运动水平加速度;分别为非线性阻尼力和非线性恢复力。
设与方程(1)等效的线性方程为:
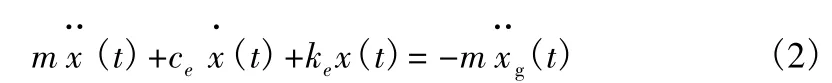
其中,ce,ke分别为等效线性阻尼系数和等效线性刚度系数。
由式(2)可知,等效线性化的基本原则就是在某种准则下合理地选取ce和ke,使所等效的线性方程的解“最优地逼近原非线性方程的解”。
考虑多自由度耗能减震的特点,欧进萍等人提出了采用割线刚度和阻尼系数等概率幅值平均值的等效线性化方法,采用双线性模型的耗能器的等效线性阻尼和刚度可按下式计算[3,4]:

其中,ce为耗能器的滞变恢复力在位移幅值为a时的等效线性阻尼;ke为耗能器的滞变恢复力在位移幅值为a时的等效割线刚度;ΔW(a)为耗能器的滞变恢复力在位移幅值为a时恢复力曲线包围的面积;xm为地震作用时耗能器的最大相对位移。
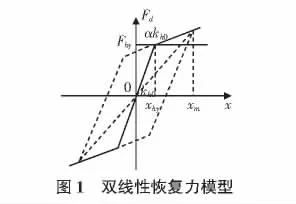
软钢阻尼器的恢复力都可近似地用如图1所示的双线性模型描述[5],于是,按式(3)相应的得到耗能器的等效阻尼和等效刚度如下:
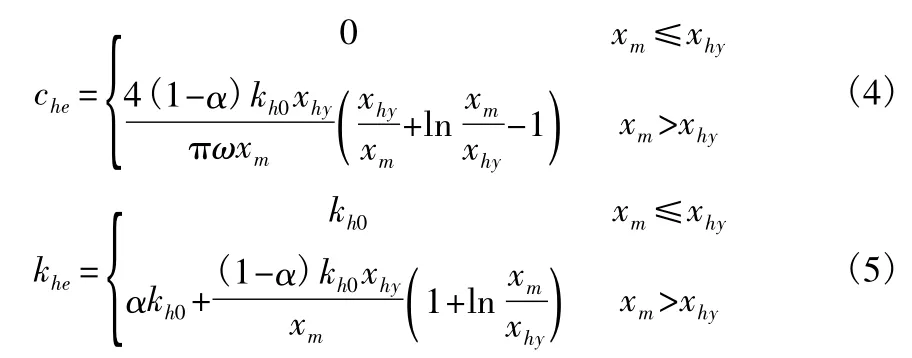
其中,kh0为滞变型耗能器与支撑串联组合单元的初始刚度;xhy为滞变型耗能器与支撑串联组合单元的屈服位移;α为滞变型耗能器的第二刚度系数;ω为耗能减震结构弹性振动的基本固有频率。
2 装有软钢阻尼器结构的仿真过程
采用基于割线刚度和阻尼系数等概率幅值平均法对软钢阻尼器进行等效线性化,求出软钢阻尼器的等效粘滞阻尼系数che和等效刚度khe,则软钢阻尼器等效线性化后的控制力可用下式表达:

加入软钢阻尼器结构的运动微分方程为:

其中,M0,K0分别为原结构的质量矩阵和刚度矩阵;C0为原结构的阻尼矩阵,采用常用的瑞雷阻尼假定,C0=α1M0+α2K0,α1,α2均为与结构体系有关的常数;{l}为n×1维单位列向量为输入到结构的地震加速度;Khe,Che分别为软钢阻尼等效线性化后的等效刚度和等效粘滞阻尼矩阵,是由式(6)中的khe和che组合形成的矩阵,可表达成下列形式:

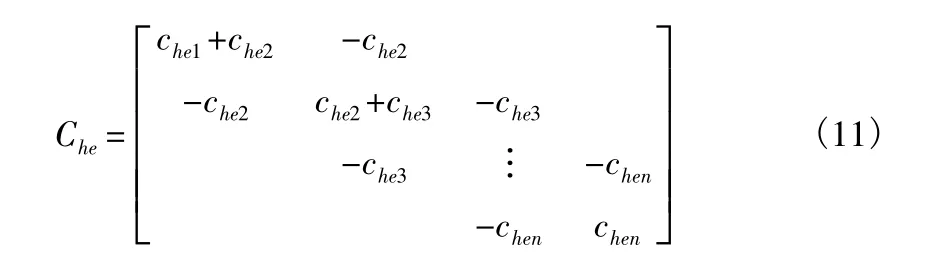
其中,khen,chen分别为第n层阻尼器的刚度总和和阻尼总和。式(7)可用状态空间描述为:

其中,u=-;0,I分别为n×n维的零矩阵和单位矩阵。
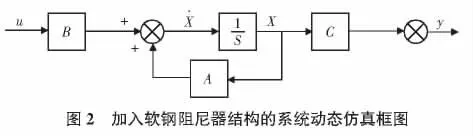
令A=0],根据该系统的状态空间描述,可以绘制系统的动态结构框图,如图2所示。根据此动态框图,在Simulink模型编辑器上用相应模块建立模型[7-9],在给定的输入下便可以对安装软钢阻尼器的结构进行动态仿真分析。
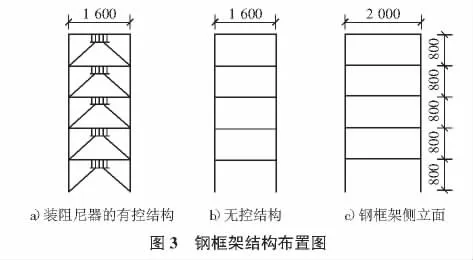
3 实例分析
为了便于说明问题,本文以某单跨5层钢框架为例,对安装有软钢阻尼器的结构在地震作用下进行Simulink动态仿真分析。5层钢框架结构布置如图3所示,层高均为800 mm,层间侧向刚度kf=250 kN/m,屈服位移uf=15 mm,结构分析中输入三条地震波,分别为El-Centro波、TAFT波和宁河天津波,峰值加速度均为0.2g。按照GB 50011-2001建筑抗震设计规范对消能减震结构参数范围的规定[10],本文选取软钢阻尼器的屈服位移ud=2 mm,ud/uf=2/15,SR=8,则耗能减震装置的刚度kd=2 000 kN/m。软钢阻尼器的第二刚度系数α=0.05,极限位移um=30 mm。
在峰值加速度为0.2g的El-Centro波和天津波作用时,分别对安装有软钢阻尼器的有控结构和未安装阻尼器的无控结构进行Simulink动态仿真分析,画出结构顶层的位移时程曲线和加速度时程曲线如图4~图7所示。

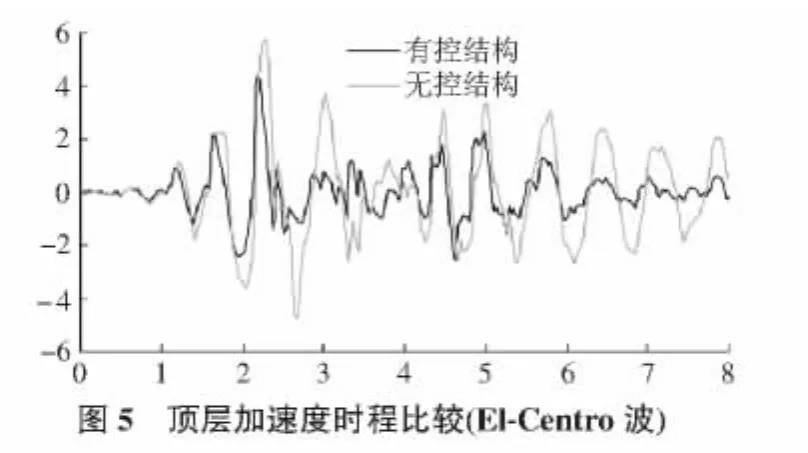


从图4~图7中可以直观地看出,装有软钢阻尼器的有控结构地震反应明显减小。
4 结语
本文通过对软钢阻尼器进行等价线性化处理,引入现代控制理论,运用状态向量和状态空间的概念,并借助于MATLAB的Simulink工具箱,对安装有软钢阻尼器的结构进行了动力时程分析。这种分析方法简洁省时,非常实用。
[1]徐赵东,郭迎春.MATLAB语言在建筑抗震工程中的应用[M].北京:科学出版社,2004:35-44.
[2]Iwan W D,Gates N C.Estimation Earthquake Research of Simple Hysteretic Structures.Journal of Engineering Mechanics Division,ASCE,No.EM3,1979:105.
[3]欧进萍,吴 斌,龙 旭.耗能减震结构的抗震设计方法[J].地震工程与工程振动,1998,18(2):122-124.
[4]欧进萍,王光远.结构随机振动[M].北京:高等教育出版社,1998:120-135.
[5]李玉顺,大井谦一,沈世钊.极低屈服点软钢阻尼器恢复力模型的研究[J].世界地震工程,2004(6):142-145.
[6]张 磊,毕 靖.MATLAB实用教程[M].北京:人民邮电出版社,2008:15-30.
[7]王正林,王胜开.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社,2005:218-222.
[8]花炳灿,陈清祥.消能减震技术在某文物保护性建筑加固工程中应用[J].建筑结构,2007(37):19-23.
[9]金来建,宋晓红,陈清祥,等.中国妇女活动中心二期工程南区酒店结构设计[J].四川建筑科学研究,2007(33):130-133.
[10]GB 50011-2008,建筑抗震设计规范[S].

