基于稳健估计的GPS 高程异常拟合模型误差分析

王 军

(西安长庆科技工程有限责任公司，陕西西安 710018)

0 引言

GPS以其精度高、速度快、经济方便的特点在平面定位中已显示了巨大优势，但是GPS高程测量的精度还不够高，在某种程度上GPS的测量优势还没得到充分发挥。由于GPS测量所求得的高程是相对于WGS-84坐标系下的高精度的大地高，而地面点高程采用正常高系统，因此，可以通过GPS测量获得的大地高，同时联测一定数量的水准点，选择合适的高程拟合模型，转换成为我国常用的正常高[2]。

GPS高程拟合的关键取决于各已知高程异常值是否存在粗差，如果存在粗差，将会引起似大地水准面拟合的失真，同时联测的水准点也可能会因为各种原因存在个别粗差，这样求得的高程异常也存在粗差，从而影响转换后的高程精度。因此采用稳健估计的方法来控制这种粗差对平差结果的影响，从而有效抵抗粗差的影响。

1 GPS高程概述及其拟合原理

大地高是地面点沿该点法线到参考椭球面的高度，大地高只是一个几何量而没有物理意义。

正高是地面点沿该点垂线到大地水准面的高度，它是一种唯一确定的数值，可以用来表示地面点的高程，但由于地壳质量分布的不均匀，因此，正高不能精密确定。

正常高是地面点沿该点垂线到似大地水准面的高度，正常高高程可以精确求得，因此，我国使用的高程是正常高。

由于GPS测量获得的是基于WGS-84坐标系下的大地高，而在实际工程中使用的是正常高，这就需要将大地高转换为正常高，在具体工作中，我们可以采用数学函数的方法通过拟合，求得该区域的高程异常变化函数，然后，再通过内插的方法求得其他点的高程异常值，进而求得正常高。

获取的测量数据可能会由于各种原因存在粗差，这就需要寻求一种具有抗粗差能力的方法来剔除这种粗差，稳健估计就是解决这一问题的最佳方法。

2 GPS拟合模型的误差分析

我们可以采用稳健估计法进行GPS拟合模型的误差分析。稳健估计就是采用不同的选权迭代方法来获得参数最理想的估值的一种方法。

在实际工程中，经常采用的是稳健估计中的M估计，由Huber提出，其稳健性与ρ(或φ)函数选择有关。

Huber提出来ρ函数为:

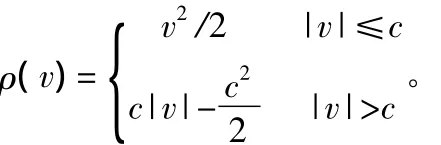
相应的权函数为:

3 实例分析

选择某测区进行试验，该测区有10个GPS控制点，其中3号点和6号点有粗差，试验时，按照不含粗差点和含3号粗差点的两种方法，分别采用最小二乘估计和稳健估计进行高程拟合求出控制网中其他待定点转换后的正常高程值进行比较，可以看出稳健估计求出的高程与不含粗差时的高程值较接近。

高程计算结果比较见表1。

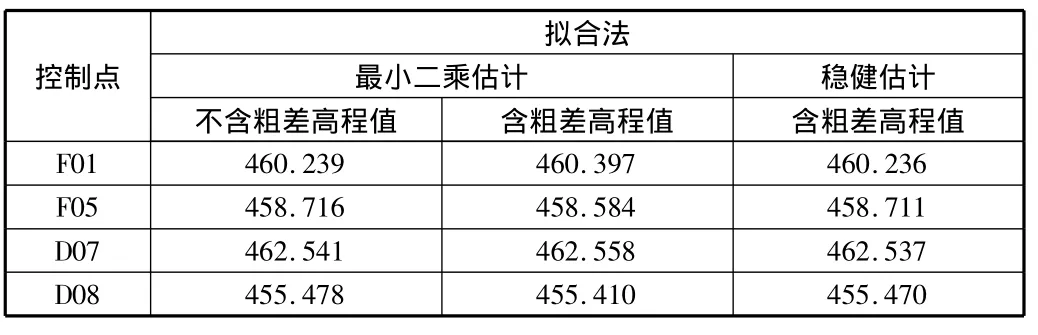
表1 高程计算结果比较表

4 结语

通过试验，可以看出稳健估计方法简单易行，具有较好的抵抗粗差影响的能力。因此，在高程异常拟合时可引入稳健估计，以保证拟合模型的可靠性。

[1]胡伍生，高成发.GPS测量原理及其应用(高等学校教材)[M].北京:人民交通出版社，2002.

[2]王利锋，蒋新华，杨晓金，等.GPS水准高程在大比例地形测量中的精度分析[J].北京测绘，2010(1):44-45.

[3]徐绍铨，张华海，杨志强，等.GPS卫星测量原理及应用[M].武汉:武汉测绘科技大学出版社，2001.

[4]赵生金，孙德厚.采用移动拟合法进行GPS网高程拟合的探讨[J].城市勘测，2007(2):55-56，66.

[5]刘 萍.新编测绘与测量数据速查处理方法与速查技术实用手册[M].北京:中国地质出版社，2006.