主成分回归在医院目标管理中的应用

谢世堂 周海迎 何 静 戴力辉△

数据分析与信息提炼在现代医院的运营管理中具有重要作用。医院管理者往往希望通过对医院以往各项运营指标数据的统计分析与提炼，获得各指标间相互作用、相互影响的数量关系，作为其制定各项管理目标的依据。医院综合目标管理涉及医疗、教育、科研、医保等众多子目标，而与各子目标相关的医院运营指标则信息更为丰富，如何通过恰当的数理统计方法，将与各管理目标相关的众多指标的数量关系提炼出来，是统计方法在医院管理中应用的一项重要课题。目前，主成分回归在医院管理中应用的研究报道非常少见，本文通过实例探讨如何利用该方法来实现指标间数量关系的建立及其模型在医院管理上的应用。

文章以某三甲医院的25个月的出院人次、门诊诊次、平均住院日、床位使用率、床位数、医护人数数据为例，阐述主成分回归在医院目标管理中的应用思路。

多元线性回归和主成分回归的选择

在医疗指标中，出院人次是医院主要的医疗产出指标之一，其大小受到医院规模指标、服务人群指标、资源效率指标的影响。本文以出院人次Y为应变量，实际开放床位数X1、医护人数X2、门诊诊次X3、平均住院日X4、床位使用率X5为自变量，通过线性回归分析来解释各指标间的相关性及关联程度。

对变量Y、X1～X5通过SPSS 13.0做相关分析，结果如表1所示。

Y与X1-X5都相关且有统计学意义。但X1～X4之间也存在相关性且有统计学意义，X3与X5存在相关性且有统计学意义。提示自变量间可能存在多元共线性。

当经典的多元线性回归无法提炼具有共线性的医疗指标的管理信息时，引入相对复杂的主成分回归便是一种选择。通过引进主成分分析来将相互关联的多个变量化成几个互不相关的综合变量，再以主成分为自变量与应变量建立回归方程，形成主成分回归分析〔1〕。这样，在保留了原自变量信息的同时，既减少了回归分析中自变量的个数，而且作为自变量的各主成分互不相关，保证了回归方程的稳定性。

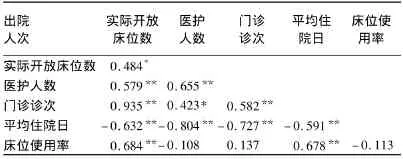
表1 变量间的相关系数

主成分回归的建立过程

1.主成分的建立

自变量X1～X5之间相关，采用主成分分析，提取包含主要信息的主成分。

如表2所示，主成分1、2已包含了自变量X1～X5的主要原始数据信息，其贡献率分别为59.644%、27.553%，主成分1、2的累积贡献率为87.197%。

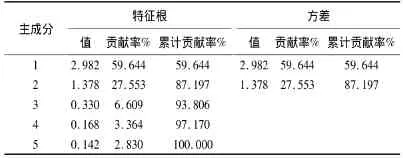
表2 主成分方差贡献率和累计贡献率

分析得到第一主成分、第二主成分与标准化后自变量之间的函数关系。第一主成分Z1=0.805X1+0.860X2+0.812X3-0.904X4+0.345X5;第二主成分Z2=-0.467X1-0.156X2+0.503X3+0.235X4+0.910X5(主成分表达式中X1-X5是原始指标通过公

为了方便计算主成分，将主成分表达式的标准化自变量替换成原始自变量。分别求出X1～X5的均数和标准差，如表3所示。

将原始自变量代入主成分表达式后，第一主成分Z1=0.04828165X1+0.00982509X2+0.00005023X3-0.84644194X4+0.03716471X5-57.00091054;第二主成分 Z2=-0.0280093X1-0.00178223X2+0.00003112X3+0.22003745X4+0.09802865X5+13.45279431。经过代入原始自变量的主成分表达式，在引入自变量数据后得到第一主成分Z1、第二主成分Z2的数据。

经过以上主成分分析后，在基本保留原数据信息的前提下，将5个具有一定相关性的自变量(X1～X5)降为2个相互独立主成分(Z1、Z2)，这就为多元线性回归分析奠定了基础。

(2)主成分回归的建立

在主成分分析后，就应变量出院人次Y、主成分Z1、Z2进行多元线性回归拟合。出院人次不服的正态分布，将Y进行对数变换后的lgY为应变量，模型拟合效果更好，见表4。

表4 模型评价参数

模型的残差的标准差为0.022，提示模型预测的稳定性较好，该值越小则反映模型预测应变量的效果越好〔2〕。

对于该模型，F=113.155，P＜0.001。说明至少一个自变量的回归系数不为0，所建立的回归模型有统计学意义。

对偏回归系数的检验如表5所示。

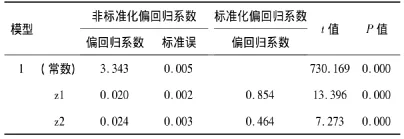
表5 模型偏回归系数的t检验结果

模型的常数项、Z1、Z2的偏回归系数分别是3.343、0.020、0.024;对 Z1、Z2的偏回归系数是否等于0的t检验结果，t值分别是13.396、7.273，P 值分别为P＜0.001、P＜0.001。据此，得到应变量lg Y的回归方程:

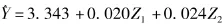
对模型进行残差分析，根据残差图观测，挑选出2个异常值，结合专业判断予以剔除。如图1所示，该模型基本符合多元线性回归的LINE条件。

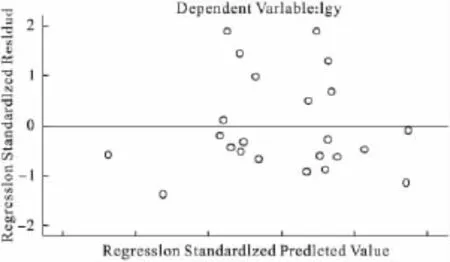
图1 残差图

回归模型的作用

1.应变量预测、应变量影响因素分析

通过主成分回归拟合，得到有统计学意义的模型。为了实际应用的可操作性，需要把主成分表达式代入主成分回归方程，以便在对应变量预测时，代入自变量X1～X5的原始数据就可以，其模型如下:

将某期的X1～X5的数据代入模型后，得到lg Y的测算值Y，并进行10为底的指数变化后，便可得到当期的出院人次的预测值。同时，可以预测各自变量在一定的区间内的变化对应变量的影响程度。

2.医院、科室年度综合目标的管理

通过主成分回归模型的应用，对医院某些指标的预测将更趋于可靠;有助于科室综合目标的管理趋向精细化、系统化;同时，有助于职能科室指导临床科室如何加强指标管理。

由于模型基于样本数据的拟合，决定了模型的拟合度局限于样本的特性，因此，当所研究的医院已经在发展方式、管理流程等影响医疗产出效率的关键因素发生变化时，模型应该根据历史数据适时再次拟合。

1.孙振球，徐勇勇.医学统计学.北京:人民卫生出版社，2002:328-329.

2.张文彤，董伟.SPSS统计分析高级教程.北京:高等教育出版社，2004:97-98.