盾构施工对土体应力扰动过程的三维数值分析
马 元,宋锦虎,付 浩
(1.上海隧道工程股份有限公司,上海 200080;2.东南大学岩土工程研究所,江苏南京 210096;3.河南城建学院土木与材料工程系,河南平顶山 467044)
城市地下空间的开发利用,是实现城市可持续发展的重要途径。城市地下交通工程深埋隧道工作面一般位于地下水位以下,施工过程必然会受到地下水的影响,同时盾构施工扰动土体从而对环境造成影响。蒋洪胜等[1]经过现场测试得知在盾构掘进接近、穿越以及远离测孔区3个施工阶段,隧道周围不同区域的土层呈现出各自不同的特征;易宏伟等[2]通过现场测试分析了盾构在推进过程中对周围土体的扰动机理;袁大军等[3]对超大直径泥水盾构掘进对周围土体的扰动进行了现场监测。由于施工现场条件复杂,造成孔隙水压力变化的因素有多种,仅根据实测值难以判断主要原因,需综合采用数值模拟和理论分析方法进行对比分析。
本文应用ABAQUS软件,采用有限元流固耦合计算方法,根据实际盾构施工过程,建立计算模型,分析盾构施工过程对周围土体的应力扰动,为减小盾构施工对周围环境的影响提供参考。
1 计算模型的建立
1.1 流固耦合计算基本原理
耦合场计算大致分为间接耦合法和直接耦合法[4]。间接耦合法分别计算渗流场和应力场,通过两场的交叉迭代分析两者的耦合效应;直接耦合法针对应力场的节点位移和渗流场的孔隙水压力建立数学模型,通过求得解析解分析两场完全耦合的效应。本文应用基于比奥固结理论的直接耦合方法[5]进行模拟计算。
在渗流—应力耦合场求解过程中,在一个时间步长Δt内,平衡方程和渗流方程形成了迭代求解基础,同时需满足位移边界条件和渗流边界条件,当单元进入塑性区后,只需将弹性矩阵用弹塑性矩阵代替并进行塑性迭代计算即可。
1.2 盾构隧道施工过程的模拟
盾构的实际施工过程较为复杂,本文对分析模型进行简化,见图1,模型包括管片、注浆层、盾构、注浆压力、开挖面推力等影响因素,不考虑盾构与土体之间接触面的摩擦力、刀盘对土体的扭矩等影响因素。开挖面推力一般取1.1~1.2倍静止土压力,在本文的分析中,中心处开挖面推力取0.29 MPa;注浆压力取0.15 MPa;泥浆密度取1.3 t/m3。
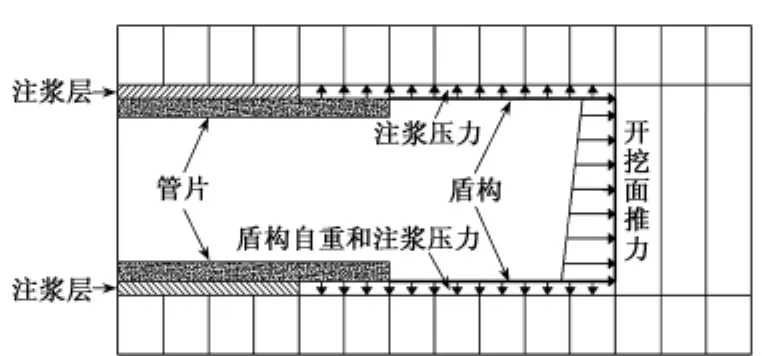
图1 数值计算模型示意
1.3 有限元模型
盾构隧道的开挖会造成开挖面附近土体主应力大小和方向的改变,需采用三维模型计算分析,并综合考虑单元数量、计算机性能和计算时间划分模型单元。模型纵向长度为60 m,分40步开挖,共有单元17 600个,单元格长度1.5 m,每步开挖1.5 m,开挖速度5 m/s。在模型的中部设监测断面。管片与土体单元之间建立接触面,以模拟两者之间的相互作用关系。地下水位取于地表。计算时首先计算初始地应力状态,此时的孔隙水压力分布即为静止水压。
1.4 模型边界条件
对于流固耦合分析,边界条件分为力学边界条件和渗流边界条件。模型的力学边界条件为:四周表面和底面为法向位移约束,上表面为自由面。渗流边界条件为模型四周表面和底面均为透水边界;衬砌处为不透水边界;对于隧道开挖面,在基本模型分析中为不透水边界,在参数分析中设定为不同边界条件以进行对比分析。
1.5 计算参数取值
计算模型中土体采用摩尔—库伦材料模型,管片为弹性材料模型,力学参数取值如表1所示。

表1 计算模型材料参数
1.6 计算模型的验证
文献[5]对上海外滩观光隧道南京东路—东方明珠区段施工时地下孔隙水的变化进行了监测分析,该区段覆土厚度为5.2~7.0 m。圆形隧道采用钢筋混凝土单层衬砌结构,衬砌内径为6.76 m,外径7.42 m,衬砌厚度0.33 m,采用土压平衡盾构进行施工。数值计算模型将土层简化为粉质黏土层,土体重度为18 kN/m3,黏聚力为 15 kPa,摩擦角为 25°,弹性模量为5 MPa,渗透系数为2×10-9m/s。监测结果与计算结果的对比如图2所示,可知,计算值与实测值吻合得较好,得到的最大超孔压接近,约为35 kPa。由于实际盾构施工存在浆液向周围土体的渗透以及盾构刀盘对土体的切割和挤压作用,会加大盾构施工对周围土体孔压的扰动范围,因此数值计算结果与实测结果会有一定差别。

图2 上海观光隧道孔隙水压力计算值与实测值对比
2 计算结果分析
2.1 隧道周围土体孔压变化过程
隧道顶部、底部、右侧土体孔隙水压力在隧道开挖过程中的变化过程如图3所示。模型中盾构开挖面为不透水边界,因此对周围土体孔压扰动较小。

图3 隧道周围超孔压变化过程
开挖面前方土体中孔隙水压力分布结果见图4,可见,随着隧道开挖,开挖面前方土体中的水头分布将会达到稳定状态,即开挖面前方地下水渗流达到稳态,计算结果与文献[6]一致,说明模型计算方法合理。
在盾构掘进过程中,隧道右侧测线上超孔隙水压力分布的变化过程见图5,隧道右侧土体中的孔隙水压力先增大,后又减小至接近初始值;在隧道开挖面通过监测断面6 m时,超孔压达到最大值。
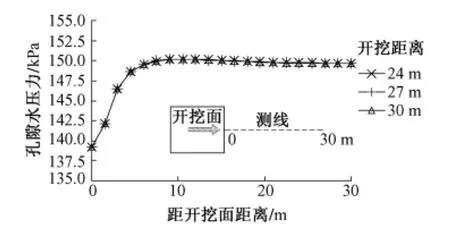
图4 开挖面前方孔隙水压力分布
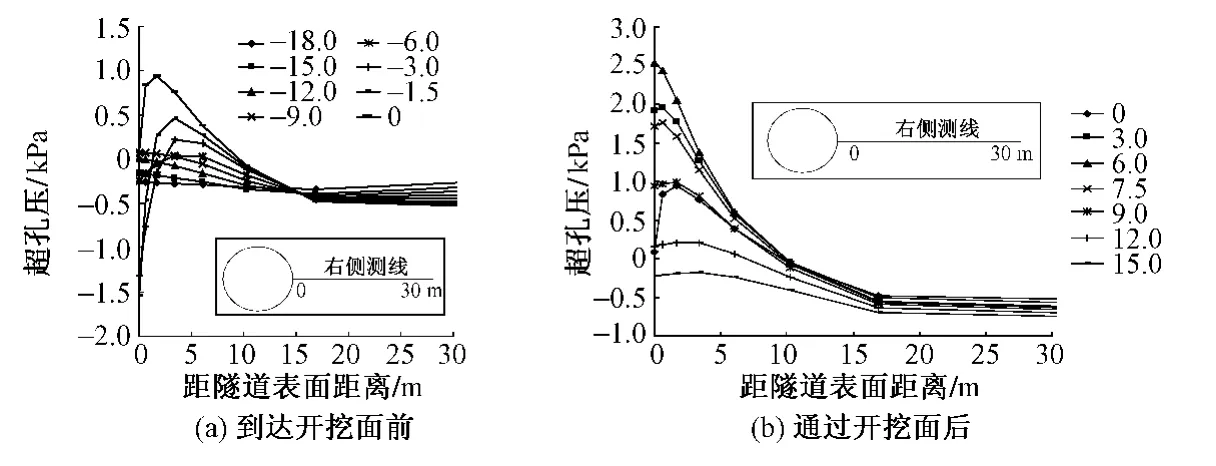
图5 隧道右侧测线孔压变化示意
在开挖面透水时,监测断面处隧道周围土体的孔压降低,当隧道开挖面通过之后,由于衬砌为不透水边界,孔压又恢复至初始静水压力状态。
2.2 测点主应力大小和方向的变化过程
各测点主应力大小和方向[7]、孔隙水压力WP的变化过程见图6~图9,其中S1,S2和S3分别为第1、第2和第3主应力,WP为孔隙水压。

图6 测点1主应力大小和方向变化过程
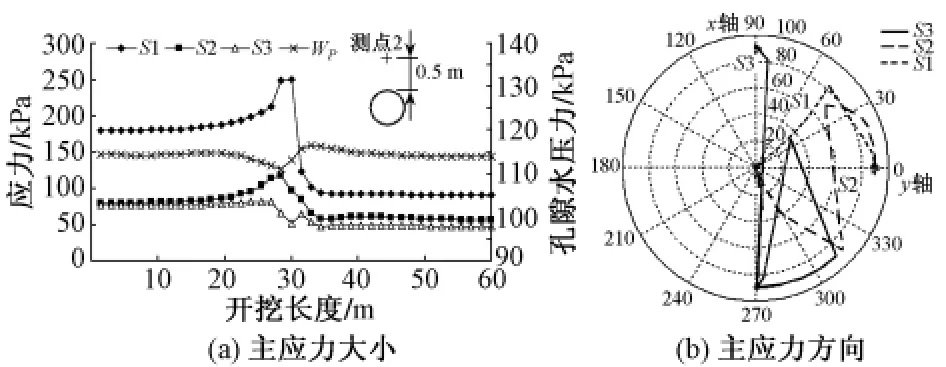
图7 测点2主应力大小和方向变化过程
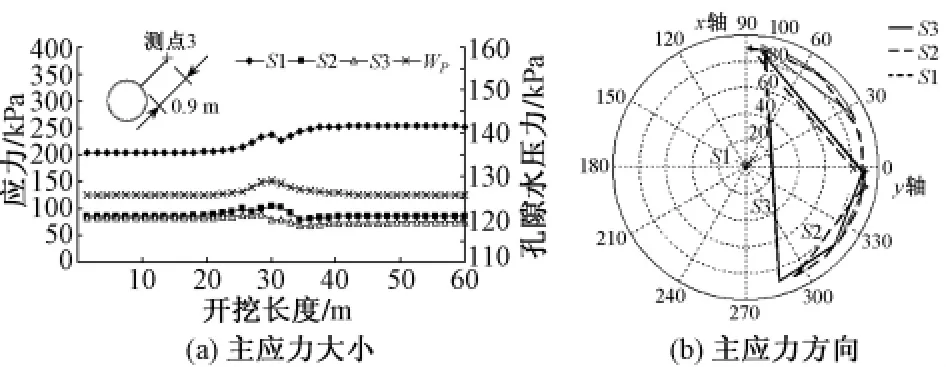
图8 测点3主应力大小和方向变化过程
由图6可见,隧道右侧土体(测点1)在开挖过程中最大主应力逐渐增大,方向不变,S2和S3逐渐减小,方向发生偏转;孔隙水压力在开挖过程中持续增大,通过开挖面之后随时间逐渐减小,直至恢复至初始孔压。由于盾构的开挖使测点1处于加载状态,从而导致其孔压升高,之后由于固结使超孔压很快消散(土体渗透系数较大)。
由图7可见,隧道上部土体(测点2)在盾构通过前,S1逐渐增大,当盾构达到监测断面时达到最大值;盾构通过后,S1,S2,S3均急剧减小,且S1方向也发生了变化,由初始的竖直方向变化为水平方向;孔隙水压力先发生了减小,后又恢复至初始值。可知隧道上部土体在盾构开挖过程中产生了卸载,从而使土体产生负的超孔压,之后由于渗流使孔压又恢复至初始值。
由图8可见,隧道右上部土体(测点3)在施工过程中S1逐渐增大,但增大值相对较小(<50 kPa);孔隙水压力逐渐增大,后同样恢复至初始值。可知测点3同样也由于盾构开挖产生了加载,使土体中产生了超孔压,之后又很快消散。
由图9可见,监测断面处隧道中心点(测点4)在施工过程中S1持续增大,孔隙水压力逐渐减小。上述计算结果是在有开挖面支护力(294 kPa)、注浆压力(154 kPa)作用下计算所得,因周围土体得到较好的支护,所以土体受盾构施工扰动相对较小。
2.3 位移计算结果
开挖过程中监测断面处隧道周围和地表A,B,C三点的垂直位移见图10,在盾构通过监测断面后,隧道顶部点下沉位移为14.5 mm,地表沉降为4.5 mm,隧道底部上浮28 mm。开挖面变形计算结果见图11,此基本模型中,由于开挖面推力取值较大(294 kPa),使开挖面上半部分土体产生了向前的凹陷位移,最大值为2.7 mm,下部土体发生了向后的凸出位移,最大值为2.3 mm。不同开挖距离时监测断面处地表沉降见图12,可知在盾构掘进面接近监测断面时,在地表产生了轻微的隆起,在开挖距离为21.0 m时(距监测断面9 m),地表隆起变形达到最大,为0.5 mm;之后地表逐渐发生沉降,最终隧道全部开挖后最大地表沉降为4.5 mm。

图10 地表沉降、隧道顶点和底点位移变化过程
2.4 管片后期固结沉降结果
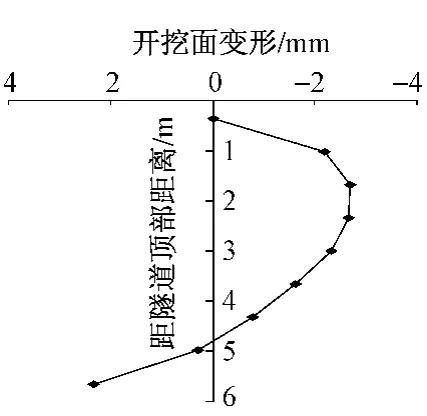
图11 开挖面变形
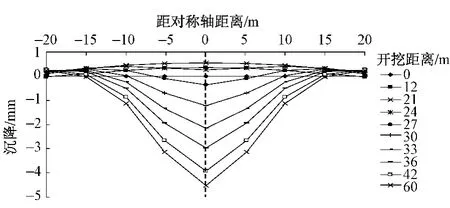
图12 监测断面处地表沉降变化过程
土体渗透系数较低时,由于隧道周围土层中的超孔压未能快速消散,造成土体的长期固结变形[8-9],对管片的长期荷载产生影响。在土体渗透系数为1.0×10-8m/s时,隧道全部开挖后,监测断面处管片内力(弯矩)随时间的变化见图13,可知管片荷载随时间持续增大,在180 d后趋于稳定。在隧道顶部建立局部坐标系,周围土体在局部坐标系下的沉降变形见图14,可知周围土层相对于管片顶点产生了随时间逐渐增大的不均匀沉降,使管片内力发生变化。

图13 管片长期荷载变化情况
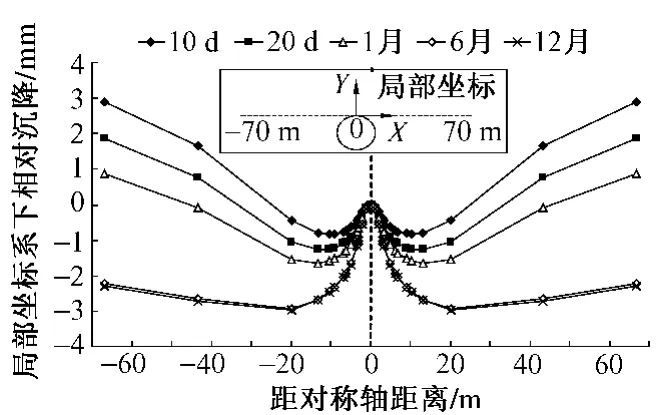
图14 局部坐标系下隧道顶部不均匀沉降
3 结论
采用三维流固耦合有限元计算方法可合理模拟水下盾构的施工过程,并可分析管片、注浆层、盾构、注浆压力、开挖面推力等影响因素对开挖面变形、地表沉降、管片荷载等的影响,模拟分析结果表明:盾构开挖使隧道两侧土体处于加载状态,孔压升高;使隧道上部土体处于卸载状态,孔压降低;盾构通过之后逐渐恢复至初始孔压。在土层渗透系数较小时,盾构施工之后土体中仍将存在较大的超孔压,造成土体长期固结变形,使管片荷载随时间增大。
[1] 蒋洪胜,侯学渊.盾构掘进对隧道周围土层扰动的理论与实测分析[J].岩石力学与工程学报,2003,22(9):1514-1520.
[2] 易宏伟,孙钧.盾构施工对软黏土的扰动机理分析[J].同济大学学报,2000,28(3):277-282.
[3] 袁大军,尹凡,王华伟.超大直径泥水盾构掘进对土体的扰动研究[J].岩石力学与工程学报,2009,28(10):2074-2080.
[4] 张欣.基于ABAQUS流固耦合理论的库岸滑坡稳定性分析[D].济南:山东大学,2005.
[5] XU Yongfu,SUN De'an,SUN Jun.Soil disturbance of Shanghai silty clay during EPB tunnelling[J].Tunnelling and Underground Space Technology,2003(18):537-545.
[6] ANAGNOSTOU G.The Effect of Tunnel Advance Rate on the Surface Settlements[C]//The 12th International Conference of International Association for Computer Methods and Advances in Geomechanics(IACMAG),Goa,India,2008.
[7] EBERHARDT E.Numerical modelling of three-dimension stress rotation ahead of an advancing tunnel face[J].International Journal of Rock Mechanics and Mining Sciences,2001(38):499-518.
[8] 缪林昌,王非,吕伟华.城市地铁隧道施工引起的地面沉降[J].东南大学学报,2008(2):293-297.
[9] 洪源.盾构法隧道施工地表沉降变形模拟分析[J].铁道建筑,2012(4):65-67.

