一种功率修正的多频空时数据自适应处理方法

杜文韬 廖桂生 杨志伟

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

机载雷达的地杂波多普勒谱展宽严重，动目标多普勒频率常淹没在杂波多普勒谱内，脉冲多普勒处理分离目标与杂波的方法将失去效果。如何有效抑制场景杂波是地面动目标检测面临的主要问题。空时自适应处理(STAP)算法[1,2]联合空间和时间两维自由度可有效提高杂波抑制性能，获得较好的最小可检测速度(MDV)。

最小方差准则下的最优STAP方法需准确已知待检测距离单元的空时相关矩阵，而实际工作环境中通常利用临近距离门的回波数据(训练样本)进行估计。文献[3]指出，相对于最优处理，独立同分布的训练样本个数大于2倍系统自由度时自适应处理器的性能损失不超过3 dB。然而在实际工作环境中，由于杂波功率分布非均匀、杂波空时谱分布特性依赖距离单元等非理想因素，导致满足独立同分布条件的样本数不足，恶化了传统全维自适应处理方法的杂波抑制及动目标检测性能。针对上述问题，存在两种解决思路，一种是在单频系统下采用降维方法和非均匀处理提高协方差矩阵的精确度，另一种是利用发射的多频信号提高样本个数。

在单频系统下，文献[4]提出了利用多分支结构插值、剔除、滤波的降维空时自适应算法，但是计算量较大；文献[5,6]结合功率挑选和相位挑选适合的训练样本，能够剔除训练样本中的强目标信号，但存在滤波器凹口展宽问题；杂波谱对齐法[7,8]以及时变加权法[9]是解决杂波空时谱分布特性依赖距离单元的有效手段，但它们均没有考虑杂波分布的非均匀问题。

相比单频多通道系统的空时数据，多频多通道系统获得空时频3维数据，信息量更加丰富。然而目前的多频信号处理方法仅利用不同频率的模糊速度差异进行解模糊运算[10,11]，或是联合多频数据检测提高检测概率[12]，没有充分利用空-时-频数据的自由度，检测性能有待提高。

综上，本文提出一种综合利用多频空时数据的自适应处理方法。该方法在分析不同频率杂波特性差异的基础上，采用杂噪声协方差矩阵重构达到自适应修正不同频率下杂波功率的目的，最后通过融合不同频率数据的空时采样协方差矩阵获得高精度的杂波子空间，能够在样本数较少情况下达到较好的检测性能。

2 信号模型

不失一般性，我们以机载预警雷达非正侧视观察体现杂波的空时特性。图1是观察示意图。其中v为载机速度，H为平台运动高度，α和β分别表示杂波地块相对阵面的方位角和俯仰角。θvcone和θacone分别表示载机速度矢量和阵列方向矢量相对于杂波的空间锥角。以位于原点位置的天线为参考通道，其他各通道与之距离分别为d1,d2,…,dM-1，这里假设为均匀线阵，有dm=m·d,d为通道间距。

图1 非正侧视观测示意图

设雷达的M个阵元沿航向排布，每个阵元可同时发射和接收K个载频的信号。给定距离单元的雷达回波数据可表示为

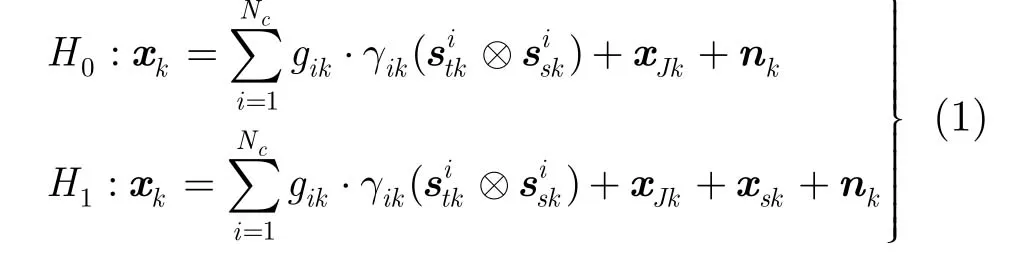
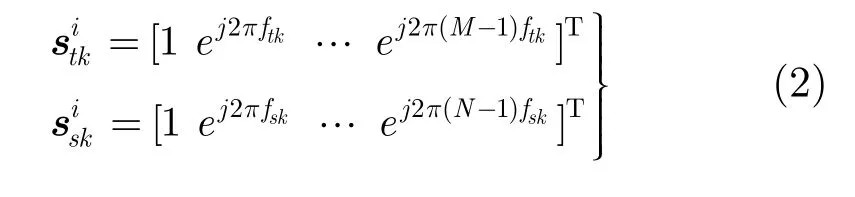
假设第k个频率下，第i个地块中含有径向速度为vr的运动目标，则动目标空间频率与该杂波地块一致，而多普勒频率存在差异，即

正是由于动目标与杂波在空时 2维域上可区分，STAP方法才可以在主瓣杂波区检测动目标。

3 多频空时数据融合

多频多通道系统下，为提高估计杂波协方差矩阵的精度，多频数据联合处理是一种有效方法。在协方差矩阵估计的过程中，训练样本需满足独立同分布性质。在样本独立性方面，由于中心频率的差异，多频数据之间满足独立性要求；在同分布方面，虽然多频数据的空时频率的比例一致，但不同频率下杂波功率差异明显：一般情况下物体的散射系数随着载频的增加而增加，以文献[13]中的24o入射角、草地背景为例，在频率3 GHz, 5.5 GHz, 10 GHz下的散射系数分别为-16 dB, -13 dB, -6 dB。因此不同频率下的样本不满足同分布要求，为联合利用多频数据进行相关矩阵估计，需对不同频率下的杂波功率进行归一化处理。

针对上述问题，本文提出一种基于杂噪声协方差矩阵分解的功率修正方法：首先计算不同频率下杂波协方差矩阵，接着根据参考频率的杂波估计功率对其他频率的相关矩阵进行修正，最后联合多频数据估计杂波协方差矩阵。

为估计杂波功率，需对杂噪声协方差矩阵进行分析。理想的杂波协方差矩阵可表示如下：

其中σp(p= 1 ,… ,r,r为杂波自由度)为杂波功率，up为对应的杂波向量，σn为噪声功率，INM为NM维的对角矩阵，“H”表示共轭转置，Σ如式(6)所示。

可以看到，特征分解获得的大特征值λp同时包含杂波和噪声的功率，小特征值对应噪声功率。

基于上述分析，我们给出多频数据功率修正空时自适应算法的具体步骤如下：

步骤1 各载频杂波功率估计

依次计算第k个载频的相关矩阵,k=1,…,K，对进行特征分解并分离大特征值与小特征值，如式(7)所示。

接着对小特征值求平均，估计每个载频下样本数据的噪声功率为

去除大特征值中包含的噪声功率值，并统计每个载频下样本数据的杂波功率为

步骤2 杂波功率均衡

步骤3 多频空时数据融合

计算功率修正的多频数据的联合相关矩阵为

利用获得的联合相关矩阵计算最优权矢量：

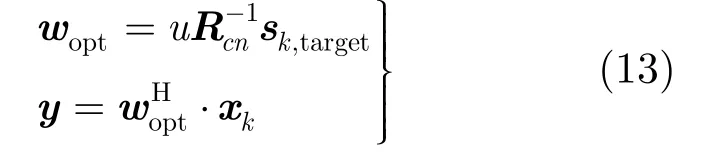
图2为功率修正的多频数据联合空时自适应处理的计算流程。

图2 功率修正的多频数据联合空时自适应处理流程图

4 仿真结果

仿真参数：机载正侧视情况下忽略载机运动误差，平台运动速度为150 m/s，雷达采用一发多收模式。同时发射两种频率的信号，中心频率分别为2.5 GHz, 3.5 GHz，天线方位上均匀划分为4个接收通道，阵元间距等于对应的半波长，快拍数为8。为了便于对比，设不同频率下的4通道积累后的信噪比SNR均为20 dB，频率1、频率2对应的CNR分别为20 dB, 25 dB。

为分析检测性能首先给出输出信杂噪比(SCNR)计算式为

其中RS为目标协方差矩阵，Rcn为杂波协方差矩阵。

在样本数足够的情况下，图3分别给出未统一功率和功率统一后两频数据联合的输出信杂噪比曲线随动目标径向速度的变化情况。目标的空间频率fsk= 0 。可以看到，由于不同频率下功率的差异，未统一功率时多频数据联合的输出信杂噪比存在损失，在低速情况下尤为严重，而两频数据功率统一后与单频自适应杂波抑制的输出信杂噪比曲线基本一致。

图4中给出了空时自适应处理的输出信杂噪比随样本数变化的曲线，作为对比，分别采用单频数据和基于本文方法的多频数据联合方法；蒙特卡洛实验次数为500；目标的多普勒频率为ftk= 0 .2，空间频率fsk= 0 。可以看到，在相同样本数下，相比于单频数据相关矩阵估计，本文的多频数据联合法可显著提高输出信杂噪比值。为使输出信杂噪比损失在3 dB以内，单频数据下需累积65个样本进行估计，而两频数据联合所需样本数为33，验证了多频数据联合的有效性。

图5给出了在样本数为50个的情况下，空时自适应处理的输出信杂噪比随动目标径向速度变化的曲线；作为对比分别采用单频数据和多频数据联合的相关矩阵估计方法；目标的空间频率fsk= 0 。可以看到，相比于单频自适应杂波抑制算法，采用本文方法的输出信杂噪比值在整个速度变化区间上均有提升，具有更好的动目标检测性能。

5 结论

在实际工作环境中，由于杂波功率分布非均匀、杂波空时谱分布特性依赖距离单元等非理想因素，导致满足独立同分布条件的样本数不足，恶化了传统全维自适应处理方法的杂波抑制及动目标检测性能。本文在多频多通道系统下，联合利用多频回波数据进行杂噪声相关矩阵估计，提高协方差矩阵的估计精度。试验结果显示在相同样本数下，基于功率修正的多频数据联合空时自适应处理方法可有效提高检测性能，验证了本算法的有效性。

图3 杂波功率对输出信杂噪比的影响

图4 单频与两频数据联合效果对比

图5 单频数据与两频数据联合效果对比

[1]Melvin W L. A STAP overview[J].IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 19-35.

[2]De Greve S, Ries P, Lapierre D F,et al.. Framework and taxonomy for radar Space-Time Adaptive Processing (STAP)methods[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1084-1099.

[3]Brennan L E and Reed I S. Theory of adaptive radar[J].IEEE Transactions on Aerospace and Electronic Systems,1973, 9(2): 237-252.

[4]Fa Rui, De Lamare C, Wang Lei,et al.. Reduced-rank STAP schemes for airborne radar based on switched joint interpolation, decimation and filtering algorithm[J].IEEE Transactions on Signal Processing, 2010, 58(8): 4128-4141.

[5]Kogon S M. Adaptive Weight Training for Post-Doppler STAP Algorithms in Nonhomogeneous Clutter[M]. UK,Institution of Electrical Engineers (IEEE) Press, 2004:359-374.

[6]曾操, 廖桂生, 杨志伟, 等. 基于样本加权的三通道SARGMTI 机载数据处理分析[J]. 电子学报, 2009, 37(3):506-512.

Zen Cao, Liao Gui-sheng, Yang Zhi-wei,et al.. Airborne data processing and performance analysis based on three aperture SAR GMTI system using weighted sample[J].Acta Electronica Sinica, 2009, 37(3): 506-512.

[7]Kreyenkamp O and Klemm R. Doppler compensation in forward-looking STAP radar[J].IEE Proceedings-Radar,Sonar and Navigation, 2001, 148(5): 253-258.

[8]Melvin W L and Davis M E. Adaptive cancellation method for geometry-induced non-stationary bistatic clutter environments[J].IEEE Transactions on Aerospace andElectronic Systems, 2007, 43(2): 651-672.

[9]Kogon S M and Zatman M A. Bistatic STAP for airborne radarsystems[C]. Proceedings of IEEE Sensor Array and Multi-channel Signal Processing Workshop (SAM),Lexington, 2000: 256-260.

[10]Li Xiao-wei and Xia Xiang-gen. Location and imaging of elevated moving target using multi-frequency velocity SAR with cross-track interferometry[J].IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1203-1212.

[11]Li Xiao-wei and Xia Xiang-gen. Multiple-frequency interferometric velocity SAR location and imaging of elevated moving target[C]. IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Texas,2010: 2810-2813.

[12]齐维孔, 禹卫东. 多载频星载MIMO-SAR系统动目标检测技术研究[J]. 电子与信息学报, 2010, 32(10): 2365-2370.

Qi Wei-kong and Yu Wei-dong.Research on ground moving target indication for spaceborne MIMO-SAR of multiple carrier-frequencies[J].Journal of Electronics&Information Technology, 2010, 32(10): 2365-2370.

[13]康世峰, 罗贤云, 葛德彪. 多波段地物微波后向散射特性分析[J]. 微波学报, 1999, 15(1): 50-57.

Kang Shi-feng, Luo Xian-yun, and Ge De-biao. Analysis of multiband microwave backscattering characteristics for terrain[J].Journal of Microwaves, 1999, 15(1): 50-57.