超宽带信道建模中基于压缩感知的解卷积算法
李德建 周 正 李 斌 翟世俊
(北京邮电大学泛网无线通信教育部重点实验室 北京 100876)
1 引言
信道建模是超宽带(UWB)通信系统的主要挑战之一,UWB系统的设计、测试和改进都依赖于对信道的理解[1]。IEEE 802.15.3a和802.15.4a都是UWB的统计式信道模型,它们的出现为工业界提供了重要动力[2]。UWB的信道建模目前仍是研究热点,且信道场景种类不断扩展[3]。2008年,中国无线电管理部门发布了UWB技术频率使用规范,规定中国UWB技术的可用频段为4.2-4.8 GHz和6-9 GHz。一个符合中国UWB频段的信道模型将促进UWB研究。信道建模中,为了获取信道冲激响应(Channel Impulse Response, CIR)的细节以及更准确地估计多径参数,需要高分辨率的信道模型,高分辨率意味着相邻多径的时延间隔要小于系统带宽的倒数。CLEAN算法[4]或其改进算法[5]就是高分辨率解卷积算法。
由于UWB信号的极高带宽,频域测量设备完成一次信道测量往往需要数秒[1]。由于频域测量时的一次扫频时间必须小于信道的相干时间,扫频点数过多限制了频域测量信道方法只能测量静态信道。压缩感知理论可以用来减轻采样负担,从而缩短一次扫频测量的时间。CS理论表明,稀疏信号可以由少量的随机线性观测,用非线性的重构算法以高概率重构[6,7]。信号的稀疏可以表现在任何域,随机观测值(采样值)的数量一般远小于原信号的采样数量,形成减采样。CS已被用于解决UWB系统的信号检测、信道估计[8,9]等问题。在文献[8]中,两个由压缩感知-匹配追踪(CS-MP)表示的方法被用于UWB-IR系统的导频辅助框架下的信道估计。
针对中国UWB频谱规范下的信道建模,本文提出将 CS-MP算法用于频域测量数据后处理,完成解卷积得到信道冲激响应。时域信道建模后续处理中,解卷积类似于信道估计。而且,本文证明了如果MP算法使用一个特定的冗余字典,则MP算法等效于CLEAN算法。通过调整字典原子的步长参数,还可以得到不同多径分辨率的CIR。实测数据处理结果证明了基于CS的解卷积算法的有效性。
2 频域测量与数据后处理
2.1 测量装置与测量环境
UWB信道可以在时域或频域测量,分别得到冲激响应h(t)或传递函数H(f)。两种测量结果理论上等价,可以通过傅里叶变换从一个域变到另一个域。本文的测量是在频域进行的。测量系统包括一个矢量网络分析仪(VNA)Agilent N5242A,两个2.3-18 GHz的全向天线,天线增益为0 dBi,两根各6 m长的Rosenberger射频电缆,一台控制VNA的计算机。
办公室场景选在工业和信息化部电信研究院。本文涉及一间办公室和两间会议室的测量数据。测量包含视距(LOS)和非视距(NLOS)两种情况,发射天线放在办公室外穿透办公室的玻璃墙体作为NLOS测量场景,如图1所示。会议室的测量数据全部是LOS情况。图中的发射和接收天线位置分别用方形和圆形标志表示。办公室的天花板是铝合金材料,图 1中上侧和左侧两面墙体(细框)材料是是双层玻璃,并且夹层中有金属百叶窗。测量过程中确保室内无人,从而测量准静态信道。在LOS情况下,发射机有两个位置TX01和TX02, NLOS时发射机有一个位置 TX03,每个发射机位置都对应着相同的21个接收机位置,如图1所示。图1所示的办公室场景信道测量数据包括 42个 LOS和 21个NLOS数据。两间会议室共测得63个LOS数据。
测量时,收发天线架设在1.5 m高的三脚架上。VNA测量的参数S21作为超宽带信道的信道传递函数(Channel Transfer Function, CTF)。VNA的发射功率固定为10 dBm,连续发射5600个离散频点,这些频点均匀分布在2.3-11 GHz的频带内,扫频间隔为 1.55 MHz,允许测量多径的最大时延扩展为643.7 ns。测量范围为1-10 m。为了减弱噪声,在每一个接收点记录 10次信道传输函数并取平均值作为该接收点的测量数据。所有测量数据都用暗室中2 m参考距离下测得的天线响应加以校准。

图1 办公室场景测量示意图
2.2 时域信道建模中的测量数据后处理
信道测量数据处理主要包括将测量的复频率响应进行傅里叶逆变换,得到对应的时域响应,再进行信道参数估计得到离散信道冲激响应,统计拟合大尺度参数和小尺度参数等。为了使UWB信道模型简单易用,假设UWB信道是广义平稳(WSS)的,h(t)是UWB信道的冲激响应,可以建模为L个多径分量(Multi-Path Component, MPC)的总和
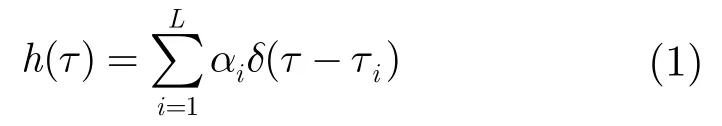

由于测量的频率范围是2.3-11 GHz,为了得到符合中国UWB频段的信道传递函数,需要频域加窗提取6-9 GHz频段的测量信号
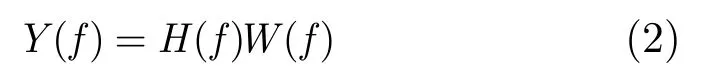
其中Y(f)是加窗后的信道传递函数,其能量主要集中于6-9 GHz,H(f)是2.3-11 GHz信道的传递函数,W(f)是频域窗函数。如果直接对目标频段的数据做傅里叶逆变换,相当于对H(f)加了 6-9 GHz的矩形窗,由于矩形窗的时延旁瓣是随时间倒数1/t下降的,时域冲激响应中会出现所谓过调和拖尾现象,导致估计的CIR有更大的RMS时延扩展。而且,如果时域窗的旁瓣较大,第1簇多径旁瓣的叠加也不利于第1径的时间定位。但加其它类型的窗会减小信道频响的带宽,造成等效时域脉冲主瓣宽度变大,降低时域分辨率。因此加窗必须在CIR的分辨率和 RMS时延扩展上进行折中,即窗的频率特性在6-9 GHz频段是平坦的,不影响测量数据的带宽;同时窗的过渡带应较平滑,以使窗的时域脉冲旁瓣较小。
由于所测频带较宽,因此可将窗的过渡带设计在6-9 GHz之外。高斯窗对应的时域脉冲仍为高斯形式,旁瓣较小,且高斯窗具有很好的时频聚集性,因此本文采用了过渡带为高斯滚降特性的类高斯窗,其频域表示为

其中a和b表示过渡带滚降特性的系数,f的单位为GHz。在10-11 GHz补零后,W(f)对应的频谱数字带宽达到了6 GHz,时间分辨率为0.167 ns。
如果直接用 VNA将测量信号转换到对应的时域形式,则结果难以应用,因为除了复时域信号的包络以外,结果不能提供其它信息。为了得到实值的时域测量信号,可将 VNA输出的复频率响应构造成共轭对称谱。时域的信道测量信号是对共轭对称谱应用IFFT得到的结果
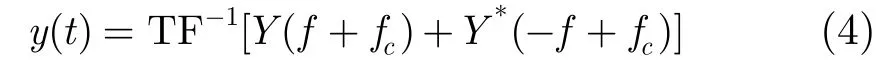
其中fc= 5 GHz, T F-1表示傅里叶逆变换。窗函数对应的时域脉冲为

经过式(4)所示的傅里叶逆变换后得到的时域响应不是式(1)描述的Dirac脉冲响应,这主要由于对频率响应进行加窗截断,窗函数对应的脉冲s(t)旁瓣发生叠加。y(t)是式(1)表示的信道冲激响应与基本波形s(t)的卷积。
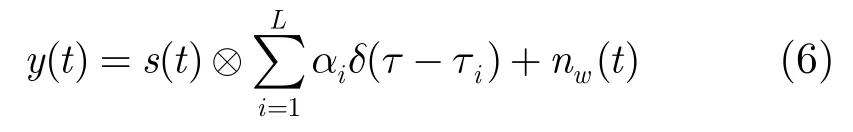
其中nw(t)是加窗后的残余高斯白噪声。采用上述处理方式的时间分辨率是1/12 GHz=0.083ns,与直接将6-9 GHz的频谱作IFFT相比,时间分辨率提高12/3 = 4倍。
3 基于压缩感知的解卷积算法
3.1 CS-MP用于加窗时域数据解卷积
为了得到CIRh(t),式(6)需要一个解卷积算法。CLEAN是一个高分辨率解卷积算法,比傅里叶分析有更高的准确性。但CLEAN算法需要VNA一次扫频很多测量点。UWB的CIR是时间稀疏的,即不是每个可分辨时延间隔内都包含多径分量,这个现象是UWB信道的基本特性,和信道中散射物体的分布有关。因此UWB信道在许多场景下是稀疏的,UWB信道的稀疏性使CS的应用成为可能。
直接在时域稀疏模型上对UWB信号应用压缩感知,重构性能较差,因为噪声会降低接收信号的时域稀疏性。将时域信号在某些基或字典上展开可以增强信号的稀疏性。文献[8]提出,设计一个参数化波形字典可以增强UWB信号表示的稀疏性。本文中,由于接收UWB信号由不同增益和时延的脉冲s(t)组成,MP的字典应由能完全表示UWB测量信号的原子构成。为了和窗脉冲波形紧密相关,字典原子应当由式(5)给出的脉冲s(t)的不同时移版本构成,即由参数化的波形来生成
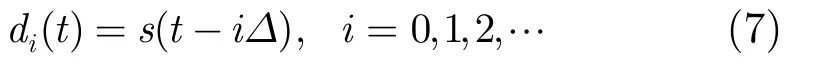
字典被定义为
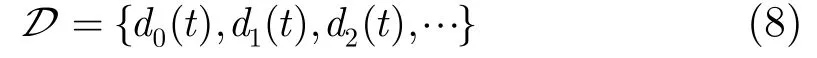
设y是式(4)中y(t)的离散表示,
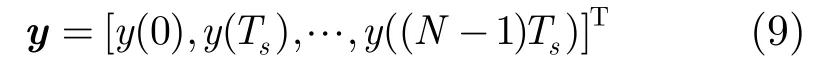
其中Ts是式(4)中y(t)的时间分辨率,N是时域响应的点数,T是转置符号。式(7)由连续时间t和D来表述,实际中两个参数应是离散化的,原子步长D可以设置为时间分辨率的整数倍,不同值的D将得到不同多径分辨率的CIR。将字典D中的原子均匀采样,得到离散字典为

于是得到

其中nw是离散形式的AWGN。式(11)显示接收信号y具有了更紧凑的表达形式。
定义测量矩阵Φ为K×N随机矩阵,矩阵元素服从零均值、单位方差的正态分布,即fi,j~N(0,1)。令g=Φy为随机投影信号,得到非相干测量值

其中Θ是稀疏向量Θ= [q,q,… ,q]T,Z是字典Ψ12Z中的原子个数。V=ΦΨ={v1,v2,… ,vZ}被称为全息字典(holographic dictionary)。假设y在Ψ上是M阶稀疏的,对于K×N测量矩阵Φ, CS理论表明,存在一个过采样因子c>1,使得只需要K:=cM个非相干测量值即可以高概率重构y。在随机投影信号g和全息字典V上应用 M范数最小化算法来重构信号。对于式(12),当噪声很小时,Θ以很高的概率是以下凸优化问题的唯一解。
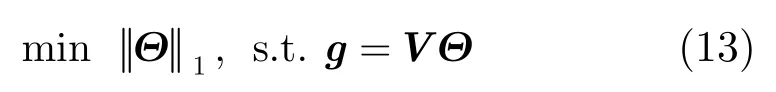
由于y是一个含噪声的信号,精确重构已不可能。然而,本文目标不是信号重构而是利用MP算法迭代时的相关运算暗含的抗噪声作用来进行信道参数估计。MP的迭代过程中,利用和g紧密匹配的字典,按多径增益大小依次找到和多径联系在一起的原子,并得到信道冲激响应的估计,从而完成解卷积。MP算法可描述如下:

步骤 2 选择全息字典中最匹配于信号残差的
步骤 3 更新信号残差值并对所选原子的系数做出估计:


3.2 与CLEAN算法的对比
CLEAN算法通过串行删除污染图纸(dirty map)先验信息(模板)之间的相关,重构出干净图纸(clean map),其中污染图纸即受噪声污染的测量信号,干净图纸指估计的CIR。令窗函数对应的时域形式s(t)为CLEAN的模板,即p(t) =s(t)。CLEAN算法的步骤描述如下[10]:
步骤 1 将脏图纸e0(t)用初始化为e0(t)=y(t),并将干净图纸初始化为c0(t) = 0 ;
步骤 2 计算归一化的互相关函数Rep(t)=en-1(t) ⊙p(t),计算=argmaxt|Rep(t)|和=Rep()(⊙表示相关运算);
步骤 3 清理脏图纸,en(t) =en-1(t) -p(t-),并将干净图纸更新为cn(t) =cn-1(t) +p(t-);
步骤 4 如果所有的<门限,转步骤5;否则,转步骤2;
步骤 5 信道冲激响应估计为(t) =cn(t)。
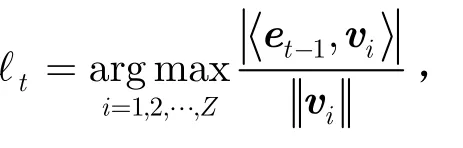

考虑到ΨTΘ= ∑idiq i和di(t) =s(t-iD),在N≫P时,有ΨTΘ≈s⊙Θ,即两个算法的步骤2实质是相同的。因此,MP算法和CLEAN算法是等价的。然而,MP是CS的重构算法,使用全息字典V,应用对象是随机投影信号g,不是使用字典Ψ应用在测量信号y上,这是CS-MP和CLEAN的主要区别。
MP的计算复杂度约为O(CLT0),其中T0是迭代次数,C是和字典大小有关的常数,L是待估计的信道抽头个数[8]。由于MP是CLEAN的等价算法,CS-MP和 CLEAN算法复杂度之间的区别与CS-MP的观测矩阵ΦK×N的大小以及两者的迭代次数有关。对于CS-MP的首次迭代,需计算g=Φy和V=ΦΨ,这使 CS-MP具有更高的计算复杂度。然而,由于字典Ψ是固定的,因此全息字典V=ΦΨ对于一组测量数据来说只需计算一次,提前计算后存储调用即可,因此算法复杂度主要由两个算法的迭代次数决定。对于余下的迭代,由于MP应用在全息字典V上,CS-MP的计算复杂度仍高于CLEAN。对于两个算法的步骤 2,VΘ的计算复杂度是O(KN)而的计算复杂度是O(PN)。因此,CS-MP的计算复杂度为O(C1KNT0),其中C1是依赖于Φ的常数,CLEAN的计算复杂度为O(PNT0)。一般地,K≫P,因此在相同的迭代次数T0条件下,CS-MP的计算复杂度要高于CLEAN。
CLEAN算法步骤 3的门限是用来结束迭代的关键参数。CLEAN的最优门限应依赖于测量时的信噪比。为了将两个算法进行对比,本文使用迭代次数T0来终止MP和CLEAN算法。
4 数据处理结果与分析
采用 2.1节描述的频域信道测量数据检验 CS-MP的解卷积性能,并针对相同的加窗时域信号应用CS-MP和CLEAN进行对比。解卷积的性能可以用重构信号相对于原始测量信号的能量捕获率来表示。
按式(3)构造类高斯窗,当a=1且b=0.093时,类高斯窗的3 dB带宽和20 dB带宽分别为3.51 GHz和 4.31 GHz,其过渡带宽度仅约650 MHz。图2(a)给出了具有高斯滚降特性的类高斯窗和具有凯泽窗滚降特性的类凯泽窗频域特性,其中类凯泽窗的参数为b=6.5, 20 dB带宽为4.7 GHz。图2(b)给出了类高斯窗、类凯泽窗和矩形窗的时域表示形式,这3种时域波形都可作为CS-MP的字典原子和CLEAN的模板。从图2(b)可以看出,矩形窗的旁瓣误差比较缓慢,拖尾现象严重。类高斯窗和类凯泽窗的旁瓣较小,且波形较相似。
图3给出了一个LOS信道测量数据的CS-MP解卷积性能。MP的迭代次数设为T0=600,图3(a)给出了一个 LOS原始测量信号的波形以及用 CSMP解卷积后的重构信号,其能量重构误差为0.057。图3(b)给出了CS-MP解卷积后的信道冲激响应。
图4和图5分别给出了LOS和NLOS情况下,CS-MP和CLEAN在不同迭代次数下的能量捕获率曲线。图4中的CS-MP曲线包括了类高斯窗、矩形窗两种情况,其中类高斯窗情况下,CS-MP的测量点个数K/N依次取0.5, 0.6和0.7。从图4和图5可以看出,两个算法的能量捕获率都随着迭代次数的上升而上升。CS-MP也会随测量值个数的增加而取得更高的解卷积性能。然而,CS-MP在迭代次数达到一定值后,能量捕获率几乎不再上升。这是因为CS中存在一个过采样因子c>1,使得至少需要K=cM个非相干测量值才能高概率重构y。然而,测量信号受噪声的影响并不是理想稀疏的,当采样点数K为一定值且K<cM时,其重构误差不会无限小,而是趋向一个固定值。
图4还给出了使用矩形窗时CS-MP的解卷积性能。可以看出,使用类高斯窗时,在同样的采样率K/N= 0 .5条件下,使用类高斯窗的能量捕获率略好于使用矩形窗的能量捕获率。因为频域矩形窗对应的时域波形旁瓣衰减缓慢,其旁瓣的叠加造成时域测量数据稀疏性有所下降,在同样的迭代次数下,采用矩形窗的解卷积性能略差于类高斯窗。从图4和图5的对比可以看出,在相同的采样率和迭代次数下,CS-MP对LOS数据的解卷积性能要好于 NLOS数据,这也是和 LOS数据稀疏性高于NLOS数据有关。
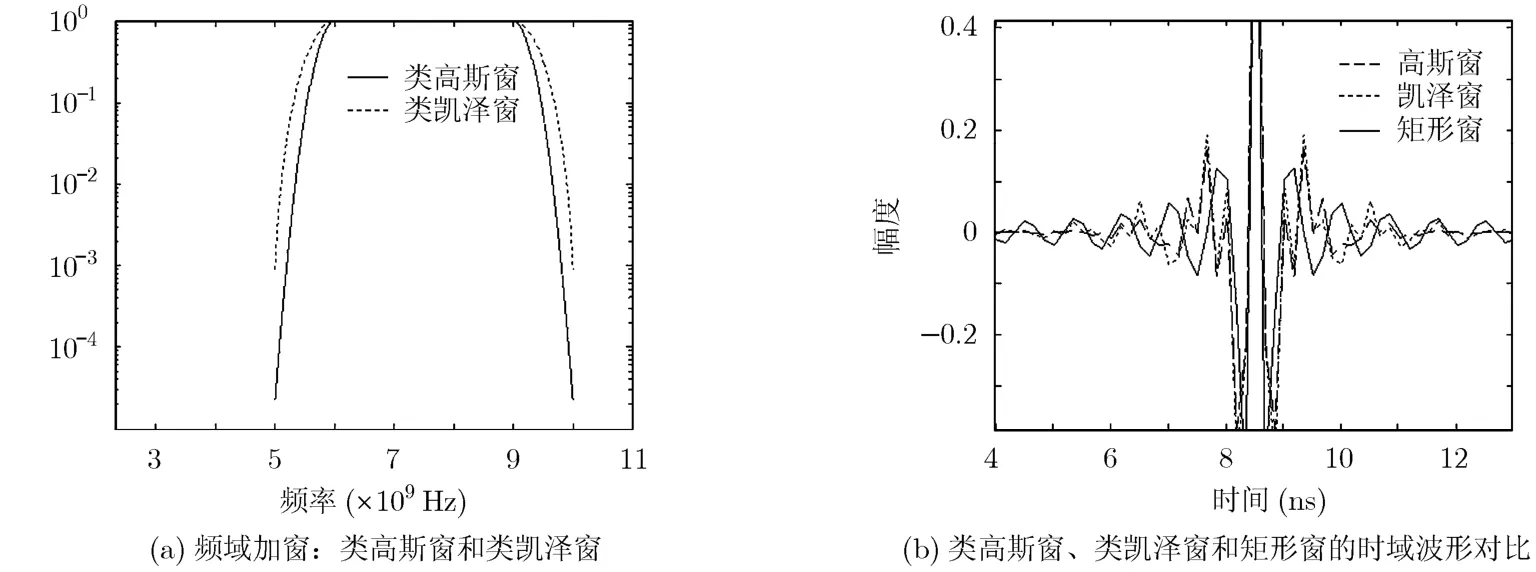
图2 类高斯窗、类凯泽窗和矩形窗的频域、时域比较

图3 LOS情况下一个信道测量的基于CS-MP的解卷积实现
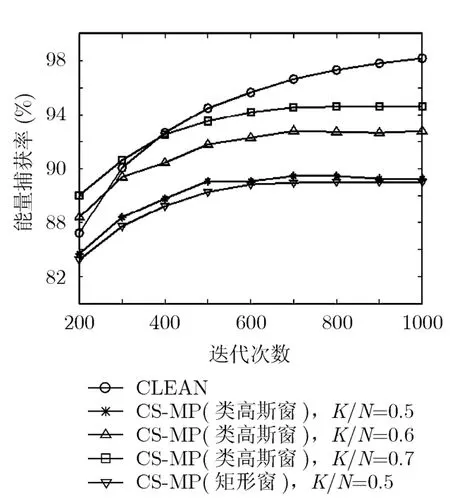
图4 LOS情况下CS-MP与CLEAN算法在不同迭代次数下的能量捕获率

图5 NLOS情况下,CS-MP与CLEAN 在不同迭代次数下的能量捕获率
5 结论
本文研究了频域测量条件下,时域UWB信道建模后处理中用到的解卷积算法。本文使用过渡带为高斯滚降特性的类高斯窗来提取频域响应,并利用类高斯窗对应的时域脉冲来增强时域响应的稀疏表达。尽管CLEAN算法是常用的高分辨率解卷积算法,但是要求信道测量提供很多的观测值。本文提出的CS-MP算法用于解卷积可以获得和CLEAN相近的解卷积性能,然而用到的观测值很少。本文还证明了 MP的原子步长等于多径分辨率时,MP等效于CLEAN算法。数据处理结果表明,CS-MP可以用于实际信道测量数据解卷积处理。
[1]Molisch A F. Ultra-wide-band propagation channels[J].Proceedings of the IEEE, 2009, 97(2): 353-371.
[2]Molisch A F. Ultra wideband propagation channel: theory,measurement and modeling[J].IEEE Transactions on Vehicle Technology, 2005, 54(5): 1528-1545.
[3]Lee J Y. UWB channel modeling in roadway and indoor parking environments[J].IEEE Transactions on Vehicular Technology, 2010, 59(7): 3171-3180.
[4]Vaughan R G and Scott N L. Super-resolution of pulsed multipath channels for delay spread characterization [J].IEEE Transactions on Communications, 1999, 47(3): 343-347.
[5]Yano S M. Investigating the ultra-wideband indoor wireless channel[C]. Proceeding of 55th IEEE Vehicle Technology(VTC’2002-Spring), Birmingham, Al, USA, May 6-9, 2002:1200-1204.
[6]Candes E J and Wakin M B. An introduction to compressive sampling [J].IEEE Signal Processing Magazine, 2008, 25(2):21-30.
[7]Donoho D. Compressed sensing [J].IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[8]Paredes J L, Arce R, and Wang Z M. Ultra-wideband compressed sensing: channel estimation [J].IEEE Journal of Selection Topics in Signal Processing, 2007, 1(3): 383-395.
[9]Li D J, Zhou Z, Zhao F,et al.. Improved channel estimation based on compressed sensing for pulse ultra wideband communication system [C]. Proceeding of International Conference on Wireless Algorithms, Systems, and Applications,2010, LNCS 6221: 330-337.
[10]Liu T C, Kim D I, and Vaughan R G. A high-resolution,multi-template deconvolution algorithm for time-domain UWB channel characterization [J].Canadian Journal of Electrical and Computer Engineering, 2007, 32(4): 207-213.

