基于ARCH类模型的人民币汇率波动特征比较

蔡晓春，邹 克

0 引言

目前世界上主要的汇率制度有两种，一种是浮动汇率制度，主要在发达国家实行；另一种是固定汇率制度，即一国货币与某种通货保持一个固定的汇率，当今世界美元充当这样的角色，采用固定汇率的国家一般为发展中国家，其目的是为了给经济提供稳定的货币、汇率环境。在2005年7月21日以前，我国人民币汇率实行的是有管理的、单一的、盯住美元的汇率制度，很长一段时间，美元对人民币的汇率一直在维持在8.27，实际上是与美元挂钩。同时，由于美元对欧元、日元、英镑等其它主要国际货币的汇率是完全浮动的，使得人民币对这些货币的汇率波动幅度更大。随着中国经济实力的增强，已有能力应付各种经济环境带来的危机，此外，经济的发展迫切要求人民币汇率市场化。在此背景下，我国于2005年7月21日实行浮动汇率制度。

汇率问题是一个复杂的问题，涉及到很多方面。怎样根据市场信息，制定中间价，客观反映市场需求，是完善人民币汇率机制的重要环节。从已有文献看，基本上是利用ARCH族模型单方面分析美元对人民币汇率的波动特征，或者从某类ARCH模型分析不同货币对人民币汇率的波动特征。少有从GARCH、TGARCH、EGARCH、ARCH-M几个模型结合，通过比较不同货币对人民币汇率的波动特征进行全面的分析，得出其收益率分布、风险溢价、非对称冲击效应等，以此来说明人民币汇率改制中存在的问题。本文试从这一角度，利用2005年7月21日至2011年5月31日的汇率数据进行分析。研究不同货币对人民币汇率的波动性特征有助于我们更深层次地了解它们之间的关系，进而为汇率机制的完善提供一定的理论支持。

1 ARCH类模型介绍

金融资产收益率具有的尖峰厚尾特性使得传统金融分析模型的假设条件不适用，基于方差变性假设的ARCH模型类模型得到广泛的应用，下面对其理论介绍。

1.1 ARCH模型

ARCH建模步骤概括为四步：（1）建立均值方程，检验模型误差项是否存在条件异方差；（2）确定ARCH模型除数和估计模型系数；（3）检验ARCH模型的参数是否是白哭噪声序列；（4）使用ARCH模型预测未来的条件方差[10]。1982年Engle给出的ARCH模型如下：其中，，上述模型记为ARCH（p）。为了保证条件方差为正与序列平稳，要求

1.2 GARCH模型

由于实际应用中ARCH模型存在以下缺点：当p较大时，参数估计不再精确，从而条件方差也不精确；条件方差为正这一条件在参数过多时往往不能保证。由于这些缺点，导致ARCH模型不实用，因此Bollerslev(1986)提出了推广的GARCH模型。该模型弥补了在有限样本条件下，ARCH模型阶数过大所带来的计算效率与精度上的不足。

上述过程称为GARCH 模型，记为{εt}～GARCH（p,q）。模型将经济变量的波动来源划分为变量过去的波动性和外部冲击，αi和βj分别反映了它们对本期变量波动的作用强度。因此GARCH（p,q）模型可以看作是观测系统的一种波动率形成机制。

1.3 TGARCH模型

金融工具的收益率和波动性存在不对称性特点，而GARCH模型不能反映刻画出这种不对称性，Glosten,Jagannathan,Ruankle(1993)提出了TGARCH模型，也称为GJR模型：

S-1是虚拟变量，如果 εt-1＜0，则取值为1，否则取值为0。式中的最后一项反映市场对不同信息反映的不同，即非对称性。不同消息的影响如下：利好消息有一个α的冲击；利空消息则有一个α+λ的冲击。λ＞0，我们说存在杠杆效应，非对称效应的主要效果是使得波动加大；λ＜0，则非对称效应的作用是使得波动减小。

1.4 EGARCH模型

Neslon(1991)提出了EGARCH模型，该模型对方差方程做的变换是：

同样，如果λ≠0，波动率是不对称的。利空消息对方差有一个α-λ的冲击；利好消息则有一个α+λ的冲击。

1.5 ARCH-M模型

在现实中，收益率和方差存在一定关系，风险越大，收益也越大，因此将代表风险的方差引入收益率的均值方程，这样的变换就是ARCH-M模型，定义如下：

2 实证分析

本文所选取的数据来源于国家外汇管理局网站，以每日中间价为基本数据，指标包括人民币兑美元、欧元、日元、港币和英镑(USD/CNY、EUR/CNY、JPY/CNY、HKD/CNY、GBP/CNY)日汇率收益序列，数据的时间跨度为2005年7月20日至2011年5月31日，剔除节假日和个别日子的数据缺失后一共得到1428个样本数据，其中，由于英镑数据从06年8月1日开始，样本数为1147个。为了得到稳定的序列数据，对收益率取对数，公式为rt=lnpt-lnpt-1，建模部分采用Eviews6软件完成。

2.1 汇率及收益率统计特征

通过人民币兑美元、欧元、日元、港币和英镑日汇率走势图，可以看出，USD与HKD是非平稳的，一直呈下降趋势。实施汇改6年时间以来，人民币处于升值过程中，人民币兑美元的汇率升值至6.4845，，截至2011年5月31日，累计升值幅度达21.66%；GBP与EUR从2008年7月开始，两者的波动走势趋于一致，表现出了很强的联动性；JAN是几种货币中唯一对人民币升值的货币。从波动程度与收益率序列看，USD/CNY与HKD/CNY的波动幅度较小，约比其余3种货币汇率小1个数量级。这归咎于美元对人民币日汇率波动被限制在千分之三幅度的政策。

图1 每100元人民币兑外汇汇率走势图

对各收益率进行描述性统计，得到表1。

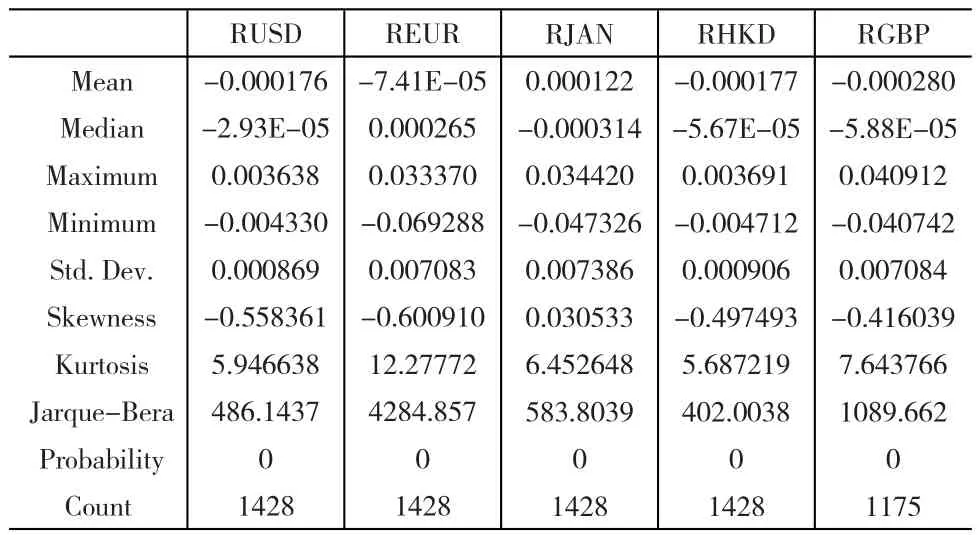
表1 人民币收益率统计特征

各收益率中，GBP的绝对收益率最大，EUR最小。USD与HKD基本上相等；在波动方面，EUR、JAN、GBP基本上持平，USD与HKD相对来说小很多；从分布特征看，USD、EUR、HKD、GBP均是左偏的，JAN基本上呈无偏状态；所有收益率的峰度均大于3，以EUR最大，序列存在尖峰的特征；从J-B统计量看，明显偏大，各序列均存在厚尾性。综上可知，收益率序列呈现尖峰厚尾、大多有偏性特征，拒绝了正态分布零假设。

另外，对各收益率序列进行相关分析发现，USD与HKD存在明显的正相关，相关系数达0.912，通过因果检验得出USD是HKD的滞后一期的格兰杰原因。EUR、JAN、GBP与USD都是负相关关系，表明美元贬值，会造成其它货币一定程度上的升值。EUR与GBP相关性（0.601）也很强，证明欧元区的两种货币变动较为一致。这几种货币中，只有JAN与EUR是相关不显著的。

通过以上分析可知，货币之间存在密切关系，因此对不同汇率的波动特征进行对比分析得出的结论更全面、准确，而且是有必要的。

2.2 平稳性检验

在建模前，首先对各收益率序列的平稳性进行检验。我们采取ADF与PP检验两种方法，单位根检验的结果如表2所示：

表2 各收益率ADF与PP检验

结果表明，ADF检验结果以及PP检验结果表明在1%显著水平下，五种汇率对数收益率序列均不存在单位根，，因此各序列都是平稳的。可以进行下一步建模。

2.3 均值方程建立与ARCH效应检验

均值方程可以根据自身序列建立，也可以导致外生变量，本文仅从自身序列分析，采取时间序列的ARMA方法。模型的选择采用AIC值和SBC值最小原则与模型简洁原则综合确定，具体分析如表3。

表3 AIC与SBC值及模型选择

通过以上原则，RUSD、RHKD序列选择ARMA（1，1）模型，REUR与RGBP序列选择ARMA（2，2）模型，RJAN序列选择ARMA（2，1），建立的均值方程如表4所示。

均值方程建立后，对其残差进行ARCH效应检验。首先对残差的平方序列进行相关性检验。从Q统计量与残差图看，五组对数收益率均值模型的残差平方序列均存在显著的相关性，因此可以推测RUSD、REUR、RJAN、RHKD和RGBP均值模型的残差序列具有条件异方差性。具体数据见表5。

表4 各序列的均值方程

表5 残差平方序列Q统计量

进一步对均值方程进行ARCH-LM检验，HKD从第1阶开始就有显著的ARCH效应，其余收益率序列需要高阶才显著。根据以往的文献在分析上一般认为各序列具有条件异方差，从残差也得出类似结论，因此我们认为模型具有ARCH效应。下面运用ARCH模型族进行建模分析。

2.4 收益率波动的ARCH类模型分析

我们运用Eviews软件对各收益序列建模，以GARCH（1，1）模型为基础，分别建立了TGARCH（1，1）、EGARCH（1，1）及ARCH-M（1，1）模型，结果及分析如下：

2.4.1 GARCH模型

从z统计量看（见表6），RJAN、RHKD、RGBP序列的均值模型某些参数变得不显著，但是ε2t-1、ht-1的参数都是显著的。从冲击的持续性看，RUSD、REUR、RJAN、RGBP的α+β值均小于1，满足参数的约束条件，说明它们的方差序列是平稳的，受到冲击后，条件方差随时间逐渐向其均值回归，但α+β值均接近于1，表明冲击的持续时间将会较长；而RHKD序列的α+β＞1，即其自身不能够保持平稳，需要外力的干扰；RUSD、REUR、RJAN、RGBP的 β 值均在0.9以上，表明过去的波动对现有波动冲击性较强，而外部冲击较弱，对条件方差的影响时间较短，相对来说，RHKD的外部冲击则要强得多。

2.4.2 TGARCH模型

运用TGARCH模型对汇率收益率的非对称性进行分析，从表7结果看，RHKD在5%的水平是不显著的。即除了RHKD不存在明显的杠杆效应外，其余序列的收益率都存在杠杆效应，从RUSD来看，当εt-1＞0时，即外汇市场有好消息时，该消息对条件方差有一个0.013倍的冲击；当εt-1＜0时，即外汇市场有坏消息时，该消息对条件方差有一个0.087（0.013+0.074）倍的冲击。坏消息有一个更大的影响，REUR的好消息冲击效应为0.035，坏消息冲击效应为时0.061(0.035+0.026)，RGBP的好消息冲击效应为0.031，坏消息冲击效应为时0.066(0.031+0.035)，这三种货币汇率的收益率都是坏消息影响大于好消息；但是RJAN与RUSD、REUR、RGBP不同，好消息对条件方差的影响为0.112，而坏消息对条件方差影响为-0.004，基本上不存在影响，即好消息的影响大于坏消息。

2.4.3 EGARCH模型

在EGARCH模型里（见表8），利空消息对方差的冲击为α-λ；利好消息为α+λ。几种货币中，RUSD与REUR的杠杆效应不显著，这与TGARCH模型不同。RHKD的好消息冲击效应为0.372(0.401-0.029)，坏消息的冲击效应为0.43(0.401+0.029)，RGBP的好消息冲击效应为0.083(0.114-0.031)，坏消息的冲击效应为0.145(0.114+0.031)，两者都是坏消息的影响大于好消息；RJAN的好消息效应冲击为0.226(0.121+0.105)，坏消息冲击效应为0.016(0.121-0.105)，坏消息的影响较小，这与TGARCH模型的结论相同。

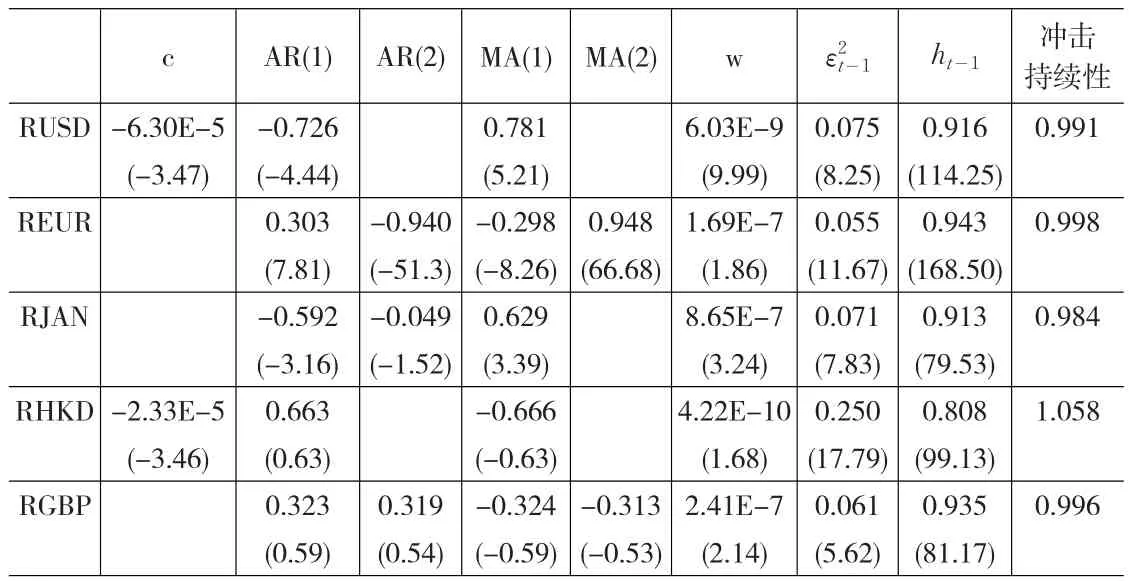
表6 各收益率序列的GARCH模型参数系数

表7 各收益率序列的TGARCH模型参数系数

表8 各收益率序列的EGARCH模型参数系数

对比两个模型，RUSD、REUR、RHKD三种货币在非对称性检验结果上不一致，RJAN与RGBP的检验结果与非对称效应是一致的。

2.4.4 ARCH-M模型

从z值看(见表9)，REUR、RJAN、RGBP的SQRT(GARCH)系数是不显著的，即说明人民币兑欧元、日元、英镑收益率的风险溢价不明显，美元与港币的风险溢价较明显，USD的GARCH项开方每增加1单位，汇率收益率就上升0.283单位；HKD的汇率收益率稍低，为0.194。美元、港币的风险溢价为正，而其余货币的风险溢价并不明显，这能够说明一些问题，虽然人民币已经实行市场化买卖，但仍与美元保持着较为密切的关系，其它货币的汇率主要通过美元换算，导致风险溢价不能体现，充分说明人民币未完全市场化，汇改制度有待进一步深化。

表9

3 结论

本文利用ARCH模型族分析了人民币兑美元、欧元、日元、港币与英镑汇率的波动率特征，根据实证结果，我们可以总结出以下几点：

（1）人民币兑美元、欧元、日元、港币与英镑汇率相互之间存在密切的关系，USD/CNY、HKD/CNY收益率相关性很强，而EUR/CNY、GBP/CNY之间的相关性也较强，这几种货币之中，只有HKD/CNY与EUR/CNY之间的相关性不显著，从此看出，货币汇率具有区域性、关联性等特点。

（2）通过残差检验，各货币的汇率收益率存在在显著的ARCH效应，各序列的分布具有尖峰厚尾的特征。从收益的波动率看，USD/CNY、HKD/CNY的具有更明显的聚集性，人民币兑美元的汇率波动性比欧元、日元、英镑小一个数量级，这是人民币兑美元汇率由于实行波动幅度管制，依然未完全市场化。

（3）从ARCH族模型的分析看，USD/CNY、EUR/CNY、JAN/CNY、GBP/CNY的外部冲击对汇率的波动影响较小，汇率的波动主要是由过去的波动所引起的，且这种冲击有一个长期的影响效应。而HKD/CNY的外部冲击效应较强，且冲击会使波动持续下去，需要借助外力才能使HKD/CNY的汇率保持平稳。

（4）总体来看，人民币汇率具有杠杆效应，USD/CNY、EUR/CNY、HKD/CNY、GBP/CNY具有相同的杠杆效应，即利空消息比利好消息会造成汇率更大的波动，意味着人民币升值的影响要大于人民币贬值的影响，但JAN/CNY具有相反的杠杆效应，即利好消息比利空消息造成汇率的波动要大。

（5）风险的溢价效应在不同货币汇率上反映不同，5种货币中，只有美元与港币的风险溢价效应是显著的，其余货币的风险溢价效应甚微。这意味着像欧元、日元、英镑的汇率波动基本上不会对人民币造成太大影响，人民币的风险收益只与美元有关，充分说明人民币外汇市场化程度不充分，主要以美元作为参照物。世界货币汇率之间存在密切关系，把握货币汇率之间的关系对人民币的汇率市场化有重要意义，中国应继续加大汇率改革的力度，做到人民币更加市场化，这是提高人民币在世界经济中的影响的重要途径之一，这样人民币才能走向更广阔的世界，走出更辉煌的未来。

[1] Poon,Ser-Huang,Granger,Clive W.J.Foreeasting Volatility in Finan⁃cial Market:A Review[J].J ournal of Economic Literature，2003,(6).

[2] Engle Robert F.Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation[J].Econometri⁃ca,1982，(50).

[3] Bollerslev.Generalized Autoregressive Conditional Heteroskedasticity[J].Journal of Econometrics,1986,(31).

[4] Nelson DB.Conditional Heteroskedasticity in Asset Returns:A New Approach[J].Economitrica,1991,(59).

[5] 吴瑜,人民币汇率波动特征实证研究:2005～2009[D].复旦大学硕士学位论文,2010.

[6] 惠晓峰,柳鸿生,胡伟.基于时间序列GARCH模型的人民币汇率预测[J].金融研究,2003，(5).

[7] 杨仁美,王靖.基于GARCH模型族的人民币基准汇率波动率的实证分析[J].粤港澳市场与价格,2009，(9).

[8] 潘红宇,金融时间序列[M].北京:对外经济贸易大学出版社,2008.