光电跟踪系统传感器延迟及控制算法研究
岳玉芳(北京应用物理与计算数学研究所,北京100088)
0 引 言
为消除目标运动扰动及载机平台对目标跟踪的影响,在光电经纬仪、地面图像跟踪装置、舰载光电瞄准装置、导弹导引头等光电跟踪系统中,普遍采用光电跟踪传感器(包括可见光电视、红外电视等)设计跟踪随动系统[1-2]。然而,一方面,光电跟踪传感器在有限的时间内必须接收足够的光子数才能达到一定的光电转换能力;另一方面,为精确跟踪快速运动的目标,对传感器采集到的图像往往需要应用各种计算量大的信号处理方式,例如多尺度方法、小波算法等,借以准确得到目标特征点。这两个方面的情况使得目前的数字信号处理器 (DSP)、大规模现场可编程器件 (FPGA)等硬件的处理能力难以满足要求,导致了可观的探测器信号处理延迟[1-2]。这种纯延迟对各个频段的输入信号均带来了非常不利的影响,容易引起系统的超调和振荡,限制了带宽的提高,制约了系统的快速性。如何克服电视纯延迟现象对系统跟踪性能的影响,如何在控制器设计中补偿电视纯延迟环节的作用一直是国内外光电跟踪系统研究的热点问题。学者研究了应用Kalman滤波器和目标位置/速度信号的顺馈闭环跟踪[3],进行坐标变换的导引头随动系统跟踪[4],将Kalman滤波器用于接收机角误差、天线座角度、测速机速度的信号处理系统[5]等。这些算法都是在特定的工作环境下,采用预测器抵消延迟时间。
本文从延迟环节线性化、经典的PI控制器设计开始,讨论考虑延迟环节的PI控制器算法设计方法以及一种新型的Kalman滤波器设计方法,该Kalman滤波器使用了Kalman状态方程一步递推和对应延迟时间的多步预测,以及通过位置预测信号差分得到速度预测信号,用于速度前馈控制,与使用Kalman滤波器的某个输出项作为速度预测信号用于速度前馈控制的方法有所不同。通过Bode图比较和Matlab环境下运行的仿真实例,充分说明这种新型Kalman控制器设计方法相对于考虑延迟环节的PI控制器设计方法更为优越,系统带宽提高,跟踪性能显著改善。新型Kal-man控制器设计方法与文献 [3]中Kalman滤波控制器设计方法得到的仿真结果也基本相当。
1 问题的提出
电视纯延迟相当于在原有系统中增加了非线性环节——延迟环节 (e-τs)。它对系统的幅频特性没有影响,只对系统相频特性产生影响,而且相频特性中随着频率提高,延迟对相位的影响增大。例如图1为实测与拟合对象的Bode图[6],两者的差异是由做频响测试时,采样频率仅为1kHz,以及采样保持器 [(1-e-τs)/s]与模数/数模转换、计算延迟 (e-τs)给实测对象引入了附加的相位延迟所致[6]。

图1 纯延迟50ms的Pade近似
图1 表明,对电视纯延迟来说,若系统设计带宽要求较高,则延迟作用对系统性能的影响较大。为方便使用线性系统控制器设计方法进行仿真,需要对延迟环节进行线性化模型逼近。本文采用PADE近似进行线性逼近,逼近的效果与所选择的PADE阶次有关。随着PADE阶次的提高,线性模型对延迟环节的近似程度提高,如图2所示。在离散控制系统中,延迟时间通常以采样时间的整数倍表示,光电跟踪自动使用最近得到的电视脱靶量,延迟环节延迟时间到来前的增益作用总是为1,故纯延迟环节的相频特性逼近是仿真中需要重点考虑的,仿真系统允许放宽对纯延迟环节幅频特性逼近程度的要求。若系统带宽要求在8Hz以内,进行2阶PADE近似基本可以满足仿真精度要求,若系统带宽要求在40Hz以内,8阶近似基本可以满足精度要求。
2 考虑延迟的目标跟踪系统PI控制器设计
2.1 控制对象模型和跟踪控制结构
在某转台跟踪系统中,控制对象为直流电机、转台负载结构,采用图3所示的速度环、位置环构成的多环路结构控制直流力矩电机[7-9]。转台跟踪系统在方位、俯仰方向的控制对象、机械谐振频率均不相同,不失一般性,本文以式 (1)方位方向的线性化模型为控制对象传递函数,进行光电跟踪系统的设计


2.2 考虑延迟环节的PI控制器
对于直流电动机伺服驱动装置最有效的控制方案,就是有一个电流内环再套上转速控制外环,再加上一个位置环来进行位置控制。这种多环路的结构多年来己在无数的应用中被证明是有效的。速度回路的频带宽度宽于位置环路的频带宽度,即速度环路的响应速度快于位置环路的响应速度。系统设计时,首先设计出速度环路使能够迅速抑制作用在系统上的干扰。然后把速度回路作为位置回路的一个环节,来设计位置回路,用来确保跟踪精度。
在多环路系统中,对速度环,被控对象GP(s)的传递函数就是式 (1)的Gm(s),对位置环,被控对象GP(s)的传递函数是速度环的闭环传递函数。
设Gc(s)为控制器传递函数,表达式为

为使校正后系统的nyquist曲线在开环截止频率ω=ωGc处通过1∠ (―180°+PM),即在ω=ωGc处能够实现要求的相角裕度PM,根据控制理论[10-11]可知
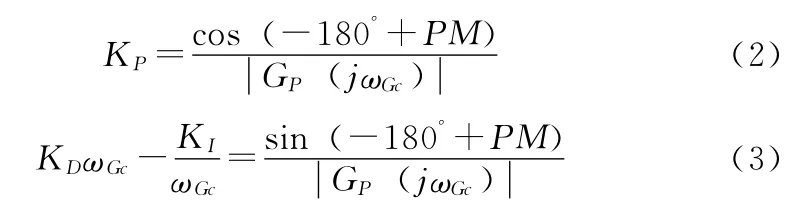
当控制器为PI控制器时,KD=0。此时,已知开环截止频率ωGc和相位裕度PM,可以应用式 (2)、式 (3)设计PI控制器。
光电传感器的电视延迟发生在位置环,因此设计速度环的PI控制器时不考虑延迟的影响,设计出速度PI控制器,得到速度闭环传递函数,作为位置环的被控对象传递函数。
同时,事先假设电视延迟时间已经通过最小二乘方法辨识出来,为已知参数。不管延迟时间的长短,都希望通过PI控制器相应于延迟时间的不同设计,使得系统的开环幅频特性为理想开环幅频特性,其相位裕度在中频段频率为处取得最大值[10]。
本文提出如下步骤,作为考虑延迟环节的PI控制器设计方法:
(1)首先设延迟时间为0,在仿真系统中设计位置PI控制器,得到系统位置环系统的开环特性,例如图4所示,其剪切频率处系统相位为-100°,即相位裕度为80°。
(2)纯延迟环节只影响系统相位,设延迟时间τ已经通过采集频响仪实验数据和应用最小二乘辨识方法得到,为已知参数。希望系统在有延迟作用下仍有45°的相位裕量,则纯延迟环节的相位在开环截止频率fc处应满足

根据式 (4),可以求出新的开环截止频率fc,重新设计位置PI控制器。
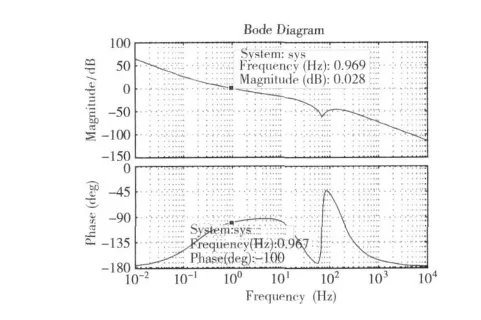
图4 延迟时间为0时的位置环开环特性
(3)根据延迟时间和新的位置PI控制器,得到系统闭环特性,验证系统稳定性及动态特性。
对图3的直流电动机方位方向伺服跟踪系统而言,应用PI控制器设计其速度环,再使用考虑延迟环节的PI控制器设计方法设计位置环,依据不同的延迟时间τ可以设计出各种位置控制器,得到直流电动机方位方向伺服跟踪系统闭环特性,当延迟时间为20ms、40ms、60ms、80ms、100ms时得到的系统闭环特性如图5所示,大于100ms的位置环闭环特性为不稳定的。

图5 各种延迟时间下位置环闭环特性
3 应用Kalman预测滤波补偿延迟作用的控制器设计
对考虑延迟环节的控制器设计而言,采用预测器进行前馈控制是一种有效方法[12-13]。这是因为:①前馈控制本身可以较好的解决一般系统普遍存在的精度和稳定性之间的矛盾,很容易将跟踪精度提高几倍甚至几十倍,但又不影响闭环系统的稳定性;②使用预测器可以预测未来时间段的信号,因而可以抵消延迟环节的时间纯延迟的影响。
在 “被动”跟踪目标的光电跟踪系统中,设计前馈控制器的前提是依据当前各种编码器、测速仪等位置、速度传感器测量值以及由电视传感器、图像处理方法得到的几个 “延迟”时刻前的脱靶量测量值,应用各种预测器方法,例如自适应滤波器、Kalman滤波器等,准确地估计 “当前”的目标运动角度、速度、加速度状态值。在此基础上,将这种 “当前”的估计值作为跟踪系统位置前馈控制和速度前馈控制的输入信号。
Kalman滤波器[14-15]作为一个线性递归滤波器,基于系统以前的状态序列对当前状态做最优估计,具有无偏、稳定的优点。在光电跟踪系统中,Kalman预测滤波广泛用于实现前馈控制和对延迟时间进行补偿,是提高随动系统稳态性能的一种优良方法。
光电跟踪系统-目标相对运动所产生的视线角运动包括方位、俯仰两个方向的数学模型。目前,有两种建立Kalman状态模型的方法,一种是在笛卡尔坐标下建立目标在三维空间中的运动方程,经过空间坐标到以跟踪系统为中心的极坐标的非线性转换,得到视线角的模型;另一种是将视线角运动看作是线性运动,非线性部分看作是噪声,得到视线角模型。前一种方法的方位、俯仰方向的模型是相互关联的,后一种方法的方位、俯仰方向模型是相互独立的。
本文采用后一种方法,目标相对光电跟踪系统的视线角运动是非线性,在Kalman滤波器中设计中采用叠加噪声的牛顿定律模型进行逼近;将方位、俯仰方向的跟踪过程分开,设计两个相互独立的Kalman滤波器,将二维滤波预测降为一维滤波预测。以方位方向为例,设Xk表示Kalman预测器的状态向量

状态x1(k)表示目标的角位移,状态x2(k)表示目标的角速度,状态x3(k)表示目标中心的角加速度,状态x4(k)表示目标中心的角加速度变化率,也称为 “角加加速度”,它与角加速度之间的关系类似于角加速度与速度之间的关系。
根据牛顿定律,设光电传感器采样时间为τ,跟踪目标的离散状态方程和测量方程为如下形式

式中:Yk——系统的m维观测序列,Wk-1——p维系统过程噪声序列,Vk——m维观测噪声序列,Φk,k-1——系统的n×n维状态转移矩阵,Tk,k-1——n×p维噪声输入矩阵,Hk——m×n维观测矩阵

对系统过程噪声和观测噪声的统计特性,假定过程噪声与观测噪声为互不相关的满足高斯分布的白噪声

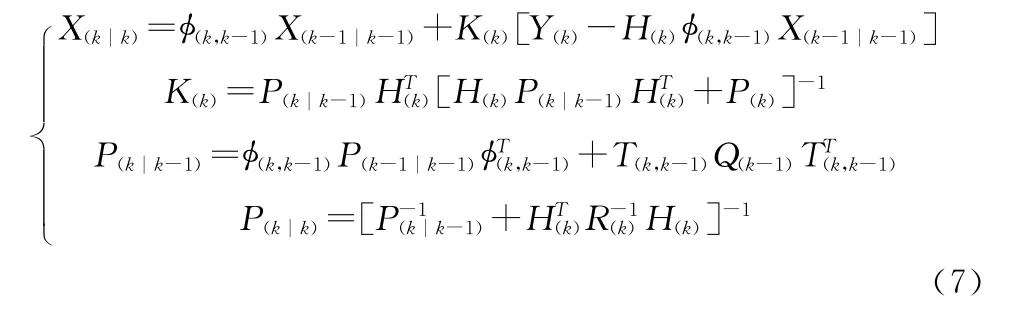
则随机线性离散系统基本Kalman一步预测滤波方程为
状态误差协方差矩阵记为P,只要给定初值X0、P0,根据k时刻的观测值Yk,就可递推计算得k时刻的状态估计Xk(k=1,2,…)。
本文采用新型的Kalman滤波预测方法:将相应时刻的目标位置信号同电视传感器信号叠加,得到有一定延迟时间的目标信号,然后将状态转移矩阵Φ设为Φk,k-1,实现从 (k-1)到k步的一步预测,得到Kalman一步滤波之后的信号,即延迟时间 (mτ)前时刻输入信号的状态平滑估计向量,再应用该向量预测 (mτ)步的信号,得到当前时刻输入信号的状态量。
在文献 [3]中,将状态转移矩阵Φ设为Φk,k-m,利用Φk,k-m进行Kalman的 (mτ)步预测,预测出当前的目标信号,实现对跟踪传感器信号的延迟时间的补偿。
本文的新型Kalman滤波预测方法与以往文献中Kalman滤波器用于补偿延迟时间的方法的区别在于:前者使用Φk,k-1进行Kalman递推,然后预测 (mτ)步,后者直接使用Φk,k-m进行Kalman递推,得到预测状态。
此外,两者的区别还有:新型Kalman滤波器控制器对Kalman滤波器的 “角位移”输出进行差分,作为前馈控制的 “角速度”输入参数,即:通过目标位置预测信号得到速度预测信号,如图6所示 (图中虚线框内为新型Kalman滤波器)。
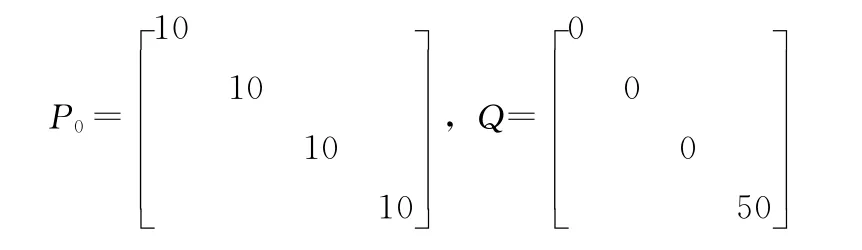
对图3的直流电动机方位方向伺服跟踪系统,光电传感器采样时间为0.02s,在某次仿真中,设置滤波器状态初值X0为零向量,状态误差协方差矩阵初值P0和噪声协方差矩阵Q参数值为
此时,当延迟时间为 20ms、40ms、60ms、80ms、100ms时,直流电动机方位方向伺服跟踪系统闭环特性如图7所示。
将图7与图5比较可知:采用Kalman滤波控制器提高了系统闭环带宽。

图6 Kalman位置预测滤波及前馈控制设计

图7 Kalman位置预测滤波及前馈控制设计
在实践中,还应用了文献 [3]的Kalman滤波控制器设计方法,实践表明:相对文献的Kalman滤波控制器设计方法,新型Kalman滤波控制器设计方法由于采用了Kalman一步递推与多步预测相结合、由目标位置预测信号得到速度预测信号两项措施,使得滤波器对初值X0、P0和Q的参数值不敏感,依赖性不强。
4 仿真实例
为方便与类似方法进行比较,采用与文献 [3]中仿真实例相同的输入信号:设目标角运动为三角函数,r(t)=1800’sin(t)+50’cos(5t),采样频率0.02s,设延迟时间为80ms。直接用脱靶量闭合时控制系统发散。采用PI控制器,得到系统稳态误差 (均方根值)为112.4’,误差曲线如图8(a)所示,采用新型Kalman控制器,得到系统稳态误差为0.247’,误差曲线如图6(b)所示,其中新型Kalman滤波器的位置预测误差为0.095’,误差曲线如图6(c)所示,速度预测误差为14.9’/s,误差曲线如图6 (d)所示。文献 [3]采用Kalman预测滤波器外推4帧的信号作为引导信号,其跟踪误差的最大值为1.3’;Kalman外推的目标位置预测误差为0.63’,速度预测误差为16.7’/s。由于本文的光电跟踪控制系统控制对象较为理想,与文献[3]的结果不能直接比较,但可以看出采用新型Kalman滤波控制器通过目标位置预测信号得到速度预测信号的方法是可行的。
5 结束语
采用Matlab/Simulink线性PADE逼近分析随动系统中光电成像传感器纯延迟。在Simulink中研究了两种控制器的设计方法:考虑延迟环节的PI控制器和新型Kalman控制器。通过Bode图比较和仿真实例可知:新型Kalman滤波控制器用于传感器纯延迟补偿具有优良性能,能够显著提高系统带宽,得到较高的跟踪精度。新型Kalman滤波控制器使用Kalman一步递推和多步预测以及由目标位置预测信号得到速度预测信号的方法是可行的。

图8 跟踪误差、Kalman预测误差曲线
[1]WANG Qiuping,ZHOU Yuan,KANG Shun.Nonlinear Kalman filter method for electro-optical tracking [J].Opto-Electronic Engineering,2009,36 (12):7-10 (in Chinese).[王秋平,周原,康顺.光电跟踪的非线性卡尔曼滤波算法 [J].光电工程,2009,36 (12):7-10.]
[2]LI Jian,JIANG Hong,SONG Long,et al.Passive locationg of maneuvering target with frequency information [J].Electronics Optics &Control,2007,14 (2):12-15 (in Chinese).[李健,蒋宏,宋龙,等.带频率信息的机动目标被动跟踪[J].电光与控制,2007,14 (2):12-15.]
[3]HUANG Yongmei,ZHANG Tong,TANG Tao,et al.Kalman filter compensation method for delay of tracking sensor in servo system [J].Opto-Electronic Engineering,2006,33(6):4-9 (in Chinese).[黄永梅,张桐,唐涛,等.卡尔曼预测滤波对跟踪传感器延迟补偿的算法研究 [J].光电工程,2006,33 (6):4-9.]
[4]ZHAO Chao.Effects of time delay and its compensation algorithm in a seeker’s servo system [J].Infrared and Laser Engineering,2008,37 (6):1066-1069 (in Chinese).[赵超.导引头随动系统中信号处理延迟的影响及其补偿算法 [J].红外与激光工程,2008,37 (6):1066-1069.]
[5]LUO Xucheng.Feedforward compound control of a single-axis tracking system using Kalman filter method [J].Telemetering and Telecontrol,2005,20 (3):1-8 (in Chinese).[罗续成.用卡尔曼滤波实现单轴跟踪系统的前馈复合控制 [J].遥测遥控,2005,20 (3):1-8.]
[6]WANG Qiang,CHEN Ke,FU Chengyu.Method for controlling fast-steering mirror driven by voice coil motor based on the closed-loop performance [J].Opto-Electronic Engineering,2005,32 (2):9-11 (in Chinese).[王强,陈科,傅承毓.基于闭环特性的音圈电机驱动快速反射镜控制 [J].光电工程,2005,32 (2):9-11.]
[7]TANG Tao,HUANG Yongmei,FU Chengyu,et al.Analysis and design of multi-closed loops control mode for tracking control system based on acceleration feedback [J].Opto-Elec-tronic Engineering,2008,35 (7):1-5 (in Chinese).[唐涛,黄永梅,付承毓,等.跟踪系统中多闭环控制模式的分析和实现 [J].光电工程,2008,35 (7):1-5.]
[8]TANG Tao,HUANG Yongmei.Application of the improved EKF algorithm in target tracking [J].Opto-Electronic Engineering,2005,32 (9):16-18 (in Chinese).[唐涛,黄永梅.改进的EKF算法在目标跟踪中的运用 [J].光电工程,2005,32 (9):16-18.]
[9]WANG Qiang,FU Chengyu,CHEN Ke,et al.Single detector compound axis control based on realtime predicted trajectory correcting method [J].Opto-Electronic Engineering,2007,34 (4):17-21(in Chinese).[王强,傅承毓,陈科,等.预测轨迹修正单检测型复合轴控制方法 [J].光电工程,2007,34 (4):17-21.]
[10]HU Shousong.Principles of automatic control [M].5th ed.Science Press,2007 (in Chinese).[胡寿松.自动控制原理[M].5版.科学出版社,2007.]
[11]WU Qi.Principles of automatic control [M].2nd ed.Tsinghua University Press,2010 (in Chinese).[吴麒.自动控制原理 [M].2版.清华大学出版社,2010.]
[12]ZHOU Yaqiang,CAO Yanwei,FENG Daowang,et al.Signal observer passive location and tracking arithmetic using look-acceleration and angle rate of changing information [J].ACTA Electronic SINIC,2005,33 (12):2120-2124 (in Chinese).[周亚强,曹延伟,冯道旺,等.基于视在加速度与角速度信息的单站无源定位原理与目标跟踪算法研究 [J].电子学报,2005,33 (12):2120-2124.]
[13]CAO Jian,ZHU Xiaocong,TAO Guoliang,et al.Adaptive robust tracking control of pressure trajectory based on Kalman filter [J].Chinese Journal of Mechanical Engineering,2009,22 (3):433-439.
[14]LIU Changyun,SHUI Penglang,LI Song.Unscented extended Kalman filter for target tracking [J].Journal of Systems Engineering and Electronics,2011,23 (2):188-192.
[15]LI Qiang,GUO Fucheng,ZHOU Yiyu.Observability of single satellite to satellite passive tracking using bearing-only measurement[J].Journal of Astronautics,2007,28 (5):1323-1330 (in Chinese).[李强,郭福成,周一宇.单个卫星观测器对卫星仅测角被动跟踪的可观测性研究 [J].宇航学报,2007,28 (5):1323-1330.]

