粗糙体变形特性对接触过程的应力与应变的影响
赖联锋,高诚辉,黄健萌
(福州大学 机械工程及自动化学院,福建 福州 350108)
两接触固体表面之间发生的摩擦、磨损和润滑与表面状态和接触情况有关,这是已为大家所熟知的事实.实验容易证实,由于存在表面粗糙度和波度,实际上两固体界面只是在一些较高的微凸体上发生接触,并由这些不连续的微小接触点变形构成了真实的接触面积.这些面积的大小和分布,决定了接触应力的大小、变形的性质和发热的程度,因此也影响接触过程的摩擦学特性[1].对此,不少学者都致力于寻求确定真实接触情况(如真实接触面积、接触点数目等),以求进一步揭示摩擦和磨损的机理,并为解决一些有关应用技术的课题提供计算方法和实用数据.
早期已经有不少学者对此进行了研究[2],但是这些以统计学参数为基础建立的接触模型对表面接触状态的计算结果往往表现出不确定性.粗糙表面分形特征的引入很好地解决了这一问题,由分形特性建立的接触模型,使表面接触的分析结果更具有确定性、唯一性.对此很多学者进行了分析并考虑弹塑性变形[3-4],但这些模型都集中在单一粗糙面与一理想平面间.同时考虑两粗糙面特性的接触模型更具有实用价值.为了简化分析,对于双粗糙面的接触问题,一些学者把表面微凸体的顶端视作球面,从两球体间的接触开始进行研究:如文献[5]对2个相互干涉球体间的摩擦交界处进行分析,假设交界处最大几何变形模式为弹性或塑性,在法向力作用下的弹性变形和接触面积与赫兹理论近似,而对于塑性交界处的结果则与Green运用滑移场理论研究的结果近似.文献[6]研究了两粗糙面间的静态接触问题,认为微凸体是服从高斯分布,结果表明:与经典摩擦理论相比,外载荷和名义接触面积对于静态摩擦系数有着较大的影响.文献[7]运用分形理论建立了两个一维静态接触模型,微凸体被定义为弹性或者完全塑性的,没有弹塑性的过渡阶段,并认为微凸体界面间的剪切应力是由相互接触面积的切向摩擦力引起的.文献[8]建立一个刚性光滑球体与一系列半径不同的椭圆形微凸体组成的粗糙面的法向接触模型,并通过实验验证了模型的接触面积预测和粗糙体的变形的正确性.
以往的粗糙表面接触模型研究已取得一定进展,但大都集中在单一粗糙面与一理想平面间或两规则形状微凸体间的接触摩擦研究上.由于接触问题中实际接触面积与摩擦磨损过程中发生的表面破坏有着极其密切的关系,实际接触面积的尺寸决定了表面的应力分布及应变情况.而实际接触过程中,各微凸体间的倾斜角对接触面积起着至关重要的影响.所以,建立双粗糙面的系统接触模型对于研究摩擦磨损的本质更具有合理性.因此本文以工程粗糙表面微观区间内的接触问题为主要研究对象,建立不同变形特性下的新双粗糙接触模型,考虑接触过程中材料的变形,分析探讨接触微凸体的应力、应变的变化情况,为进一步求解摩擦发热及摩擦磨损问题奠定基础.
1 法向接触模型的建立
1.1 粗糙表面及其接触的建模
客观准确地表征粗糙表面是摩擦学研究的重要条件.在摩擦学中,粗糙表面的轮廓曲线可以用 Weierstrass-Mandelbrot(简称 WM)函数[9]实现随机粗糙表面的数字表征,本课题组前期已经完成由分形粗糙表面构造一个三维实体模型,如图1所示,有关分形粗糙表面的生成详见文献[10].
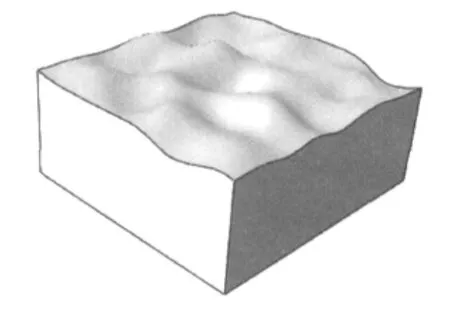
图1 三维分形表面粗糙体Fig.1 Solid model with fractal surface
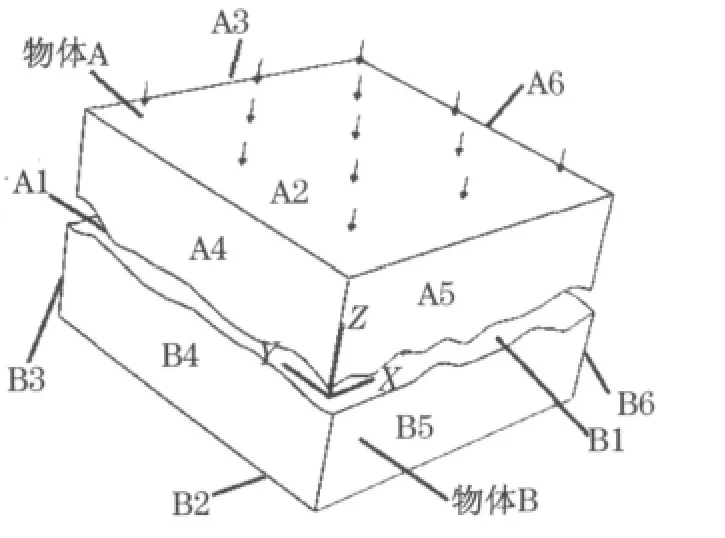
图2 双粗糙表面接触模型Fig.2 Contact model between two rough surfaces
1.2 接触模型及结构边界的建立
建立双粗糙表面的接触模型如图2所示,图中A1,B1分别表示物体A,B的摩擦工作表面,A2,B2分别表示物体A,B的背面,A3,A4,A5,A6,B3,B4,B5,B6分别表示物体 A,B的四个侧面.对接触分析过程做如下假设:①材料为各向同性,②未考虑温度的影响.
对于接触过程中的屈服准则,韧性材料运用Von-Mises屈服判据比较适合.对于三维应力空间,Mises屈服条件表示为
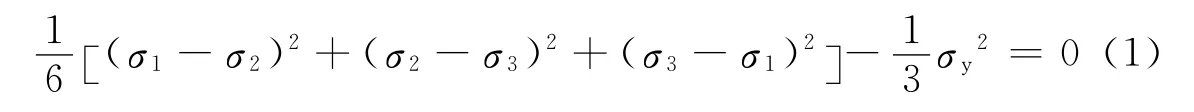
式中:σ1,σ2,σ3为3个主应力,且σ1≥σ2≥σ3;σy为材料的初始屈服应力.
法向表面接触是滑动摩擦的初始状态,根据材料的不同变形特性,本文分别建立两种不同接触特性的摩擦副模型进行分析:弹塑性-刚性(PR)和弹塑性-弹塑性(PP),粗糙体A具有弹塑性变形特性,粗糙体B具有刚性体和弹塑性变形特性.对于PR模型,由于假设实体B为刚性体,实际计算中取实体B上一点建立参考点RP,采用刚体耦合约束将实体B约束成刚体.接触模型中,具体结构边界条件如下:
粗糙体A:

式中:p为施加的均布法向载荷,MPa;My,Mx,Mz分别为y,x,z向转矩;uy为y向位移.
粗糙体B:

式中:ux,uz分别为x,z向位移.
2 算例分析
2.1 材料参数
钛合金具有质量轻、强度大、耐热性强、耐腐蚀等许多优良特性,被誉为“未来的金属”,是具有发展前途的新型结构材料.钛及其合金不仅在航空、宇宙航行工业中有着十分重要的应用,在现代航空等工程领域应用非常广泛,所以本文两粗糙体选用钛合金作为分析材料,其参数为:密度ρ=4 420kg·m-3,弹性模量E=115GPa,泊松比ν=0.31.考虑粗糙体的弹塑性变形,采用DCS-200型微机控制电子万能实验机对钛合金材料进行压缩实验,图3为材料的应力-应变曲线图.
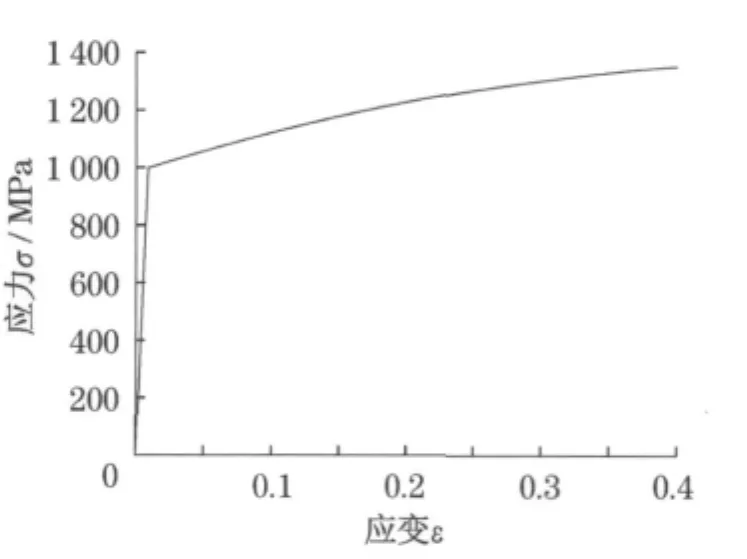
图3 真实应力-应变曲线Fig 3 True stress and true plastic strain curve
2.2 分析与讨论
由于存在表面粗糙度,实际上两固体界面的接触只是在一些较高的微凸体上,这些微凸体承受了较高的载荷,这些不均匀分布的接触压力对滑动过程的摩擦与磨损等都有重要影响,所以对于这些微凸体在接触过程的应力分布及应变分析具有非常重要的意义,本文分析过程的外载(均布载荷)p=40MPa.
2.2.1 接触表面的应力分析
图4a,b表示PR模型中粗糙实体A粗糙表面的Von-Mises等效应力σV-M分布.
图5a,b表示PP模型中粗糙实体A粗糙表面的Von-Mises等效应力σV-M分布.
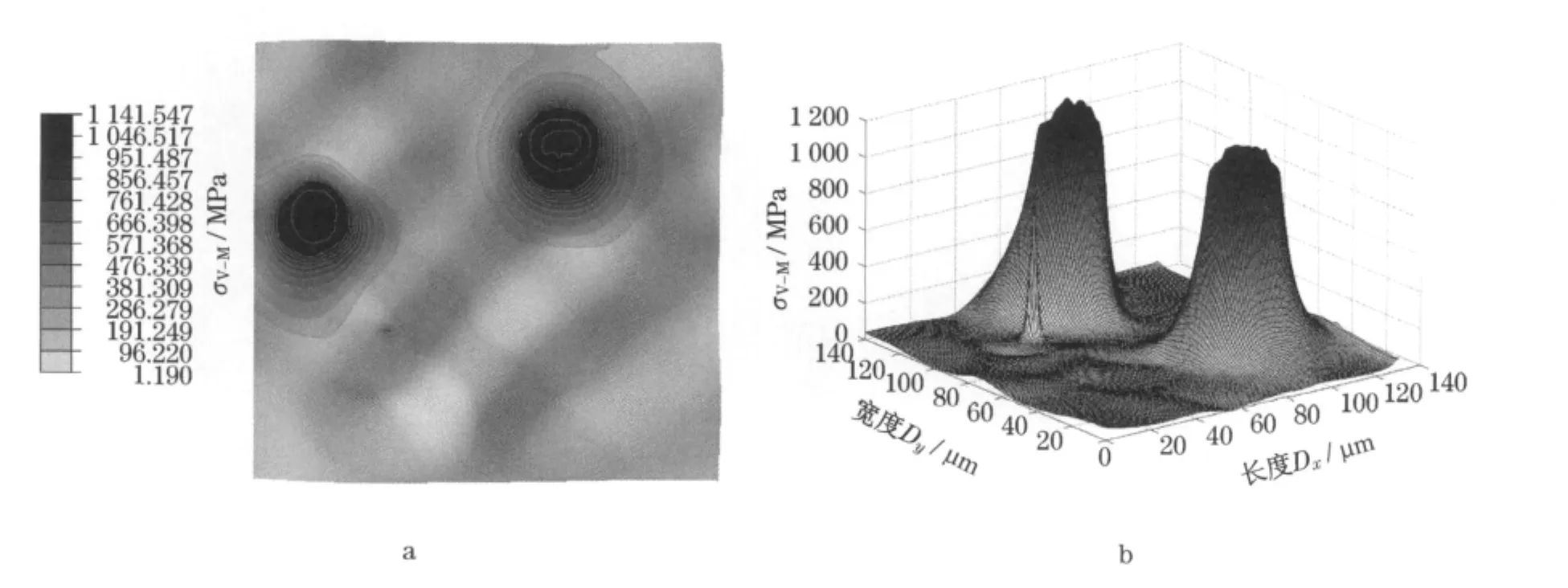
图4 PR模型中粗糙实体A粗糙表面的Von-Mises等效应力σV-M分布图Fig.4 Von-Mises stress distribution of the rough surface of solid A for PR model
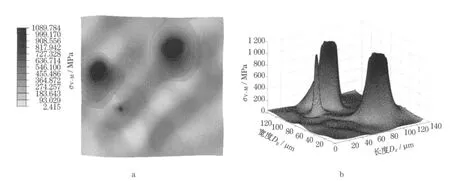
图5 PP模型中粗糙实体A粗糙表面的Von-Mises等效应力σV-M分布图Fig.5 Von-Mises stress distribution of the rough surface of solid A for PP model
从图4和图5可以看出粗糙表面的接触具有离散性,表面上只有个别地方承受作用在物体上的载荷,这使得实际接触面积非常小,个别地方承受的应力较大.从Von-Mises等效应力的三维立体图可以发现应力主要集中在两个最先接触的微凸体上,但是最大值并非在微凸体的顶点位置,而是在微凸体肩部的位置,这是因为双粗糙表面间的微凸体顶点之间不一定恰好对齐,一般成对微凸体的接触发生在其肩部位置而非顶点位置,为解释滑动过程的磨损断裂提供了很好的理论依据,也更加符合实际中的粗糙表面接触情况.
对比模型PR和PP,PR模型中粗糙实体A微凸体所受的最大Von-Mises等效应力值比PP模型的大,这是因为在PR模型中假设粗糙体B为理想刚体,所有的载荷必须全部由粗糙实体A来承担,在相同的外载条件下,粗糙体A的接触表面上承受的应力相对就比较大.
2.2.2 等效塑性应变随深度的变化分析
众所周知,塑性变形是接触状态、摩擦类型的一个标志.塑性变形的分布反映了摩擦表面的受力特点.塑性变形是摩擦表面破坏的一个主要原因,对磨屑的形成和磨屑的尺寸大小有直接的影响.由应力分析可知双粗糙表面法向接触时刻,表面只有个别微凸体进行接触,那么对于这些个别接触区域的表面及表层以下的等效塑性应变进行分析,有助于对滑动过程的摩擦、磨损机理有更全面的认识.本文选取微凸体表面的两个不同接触位置(如图6)设置路径,分析塑性应变随深度的变化规律如图7和图8.
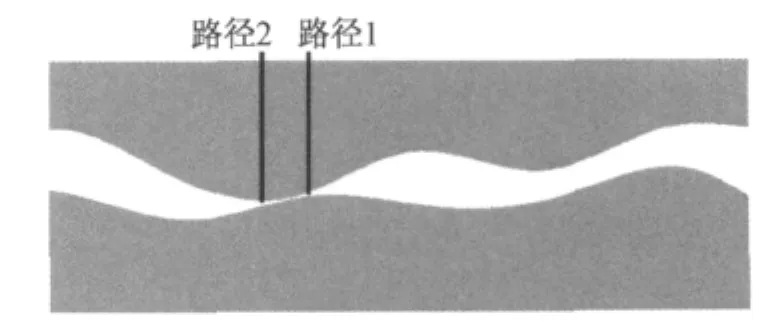
图6 微凸体接触表面的两个不同接触位置Fig 6 Two different paths of rough solid
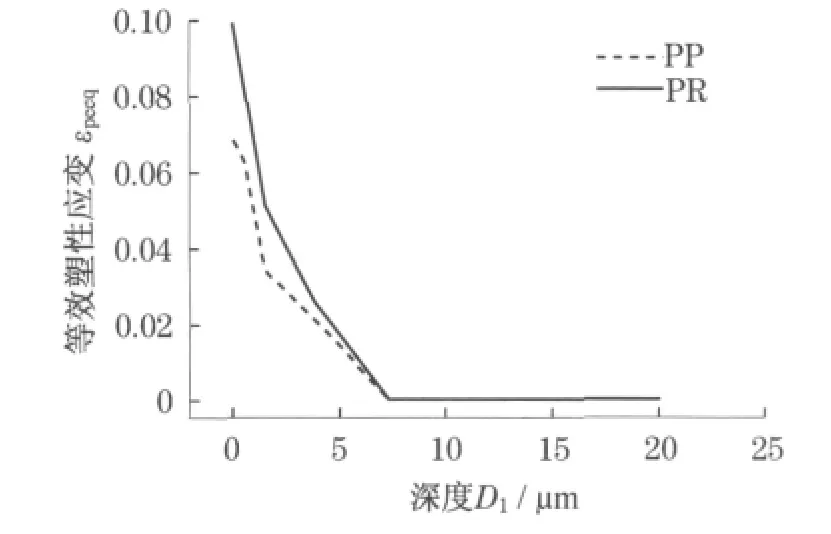
图7 路径1的等效塑性应变随深度的变化曲线Fig 7 Equivalent plastic strain of the path1 versus different depth of the rough solid
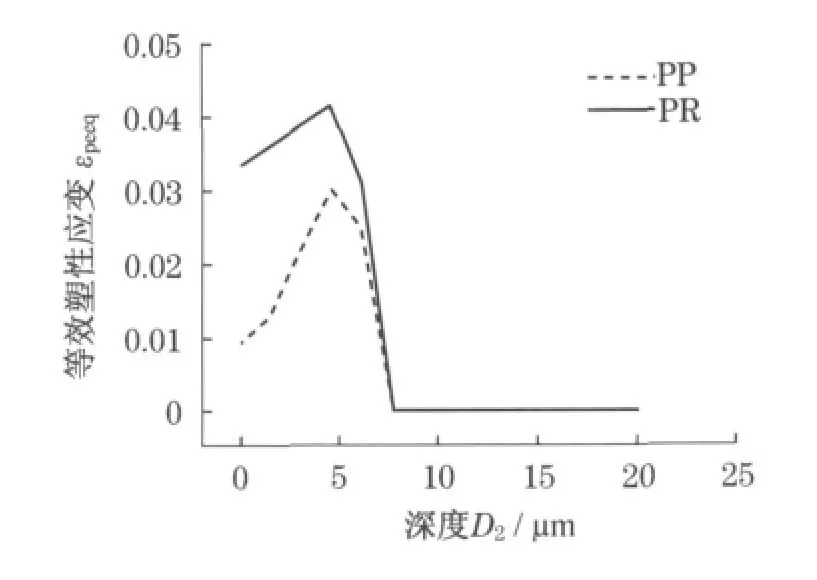
图8 路径2的等效塑性应变随深度的变化曲线Fig 8 Equivalent plastic strain of the path2 versus different depth of the rough solid
图7表示路径1(通过微凸体肩部节点)的塑性应变量沿深度的变化曲线,从图7可以看出在加载过程中,摩擦表面上的塑性变形程度最严重,随着与表面距离的增加,塑性变形程度逐渐下降.图8表示路径2(通过微凸体顶部节点)的塑性应变量沿深度的变化曲线,从图8可以看出在外载作用下,微凸体的某一次表层中(其深度约5μm)塑性变形达到最大值,随着深度的增加,塑性变形程度有大幅度的下降.等效塑性应变在不同位置沿深度的变化,呈现出不同的规律,尤其是微凸体顶点区域沿深度方向的最大等效塑性应变都是发生在次表层中.根据摩擦磨损理论[11],在摩擦滑动过程中,材料表层下的塑性应变将会导致材料表层中的夹杂或微观缺陷周围萌生微孔和裂纹源.
对比两种模型的塑性应变量沿深度的变化规律,可以看出PR模型的塑性应变比PP模型的较大.
3 结论
本文通过W-M函数生成粗糙表面,由此构造了一个新的双粗糙体接触模型,模拟仿真了双粗糙体在法向载荷作用下的接触过程,对粗糙表面的应力分布及应变随深度的变化进行了分析,得出了以下结论:
(1)双粗糙接触表面的应力主要集中在个别的微凸体上,其最大值不在微凸体的顶点位置,而是在微凸体肩部的位置,为进一步解释滑动磨损分析提供重要的依据.
(2)等效塑性应变在不同位置沿深度的变化,呈现出不同的规律,微凸体顶部区域的最大等效塑性应变都发生在次表层.材料表层下的塑性应变将会导致材料表层中的夹杂或微观缺陷周围萌生微孔和裂纹源.
(3)对比不同变形特性的模型,PR模型的最大应力和等效塑性应变值都大于PP模型.
粗糙表面接触是滑动摩擦的初始状态.通过模拟双粗糙表面间的接触过程,有利于对双粗糙体滑动过程中微观裂纹的萌生、扩展和断裂现象进行进一步的探索和认识.
[1]周仲荣.摩擦学发展前沿[M].北京:科学出版社,2006.
ZHOU Zhongrong.The development frontier of triboloy[M].Beijing:Science Press,2006.
[2]赖联锋,高诚辉,黄健萌.粗糙表面滑动摩擦接触模型研究的进展[J].中国工程机械学报,2011,9(2):134-138.
LAI Lianfeng,GAO Chenghui,HUANG Jianmeng.Advances on sliding frictional contact model of rough surfaces[J].Chinese Journal of Construction Machinery,2011,9(2):134-138.
[3]PEI L,HYUN S,MOLINARI J F,et al.Finite element modeling of elasto-plastic contact between rough surfaces[J].Journal of the Mechanics and Physics of Solids,2005,53(11):2385-2409.
[4]MAJUMDAR A,BHUSHAN B.Fractal model of elastic-plastic contact between rough surfaces[J].ASME Journal of Tribology,1991,113(1):1-11.
[5]LISOWSKI Z,STOLARSKI T.An analysis of contact between a pair of surface asperities during sliding[J].J Appl Mech,1981,48(3):493-499.
[6]KOGUT L,ETSION I.A static friction model for elastic-plastic contacting rough surfaces[J].ASME Journal of Tribology,2004,126(1):34-40.
[7]YANG J,KOMVOPOULOS K.A mechanics approach to static friction of elastic-plastic fractal surfaces[J].ASME Journal of Tribology,2005,127(2):315-324.
[8]JAMARI J,ROOIJ M B,SCHIPPER D J.Plastic deterministic contact of rough surfaces[J].ASME Journal of Tribology,2007,129(4):957-962.
[9]YAN W,KOMVOPOULOS K.Contact analysis of elastic-plastic fractal surfaces[J].Journal of Applied Physics,1998,84(7):3617-3624.
[10]黄健萌,高诚辉.弹塑性粗糙体/刚体平面滑动摩擦过程热力耦合分析[J].机械工程学报,2011,47(11):87-92.
HUANG Jianmeng,GAO Chenghui.Thermo-mechanical research on frictional sliding between elasto-plastic rough solid and rigid flat[J].Journal of Mechanical Engineering,2011,47(11):87-92.
[11]邵荷生,曲敬信,许小椂,等.摩擦与磨损[M].北京:煤炭工业出版社,1992.
SHAO Hesheng,QU Jinxin,XU Xiaolu,et al.Friction and wear[M].Beijing:China Coal Industry Publishing House,1992.

