国防实力视角下军备竞赛实证分析
闫仲勇 陈 波
引 言
引起两国之间爆发战争的原因是多种多样的,但是在这众多的原因中,军备竞赛是一个很重要的原因,军备竞赛仍是新世纪对世界和平的重大威胁。所谓军备竞赛是指国家(地区)间争相获得相对于对方的国防实力或武器装备优势的互动动态过程①[美]托德·桑德勤,[英]基斯·哈特利.国防经济学手册(第二卷).姜鲁鸣等译.经济科学出版社,2011。军备竞赛一直是国际关系领域的重要问题,为研究各国的军备竞赛情况,需要建立相应的军备竞争模型,其中,理查森军备竞赛模型就是研究军备竞赛最著名的模型之一,也是最有影响的正式模型之一。该模型在理论层面解决了各国存在军备竞赛以及处于均衡状态的条件,但由于缺少国防实力或武器装备方面的数据,关于军备竞赛的实证分析很少,我国与其他国家(地区)之间是否存在军备竞赛,“中国军事威胁论”是否成立;世界主要国家(地区)之间是否存在军备竞赛,我国经济建设的国际环境是否稳定,这些问题的研究均需要对各国(地区)之间的军备竞赛进行定量分析。为此,本文采用1979—2005年中国、美国、日本、印度、俄罗斯和中国台湾的国防实力的数据①数据测算见:闫仲勇,陈波.基于永续盘存法的国防实力测度与国际比较.世界经济与政治论坛,2011(2),在理查森军备竞赛模型的基础之上,通过建立协整模型和格兰杰因果检验模型得到一个改进的理查森线性动态模型,并采用这个改进的模型结合理查森军备竞赛模型研究了中国、美国、日本、印度、俄罗斯和中国台湾之间的军备竞赛情况,同时验证了存在军备竞赛的国家(地区)是否具有稳定状态。
理论假设和数据分析
本文在建立军备竞赛模型时,做出以下理论假设:第一,只从总的国防实力上分析军备竞赛,不涉及具体的军备竞赛,例如核竞赛、太空竞赛等。第二,只考虑两国(地区)之间的军备竞赛情况,不涉及军事联盟间的军备竞赛问题。第三,利用一国(地区)国防实力变化对另外国家(地区)国防实力变化的反应来说明两国(地区)之间的军备竞赛,只有在两国(地区)国防实力变化存在正的双向关系,即回归系数均为正且显著的情况下,两国(地区)之间才存在军备竞赛关系。
由于是时间序列,在回归之前需要分析数据的平稳性,本文利用ADF和PP检验②高铁梅主编.计量经济分析方法与建模——EViews应用及实例(第二版).清华大学出版社,2009,对各变量进行了单位根检验,结果见表1和表2。为消除异方差性,本文对中国、美国、日本、印度、俄罗斯和中国台湾国防实力取指数对数,分别记为LCH、LAM、LJP、LIN、LRU和LTW,一阶差分后的数据分别记为DLCH、DLAM、DLJP、DLIN 、DLRU 和 DLTW,二阶差分分别记为 DDLCH、DDLAM、DDLJP、DDLIN、DDLRU和DDLTW。
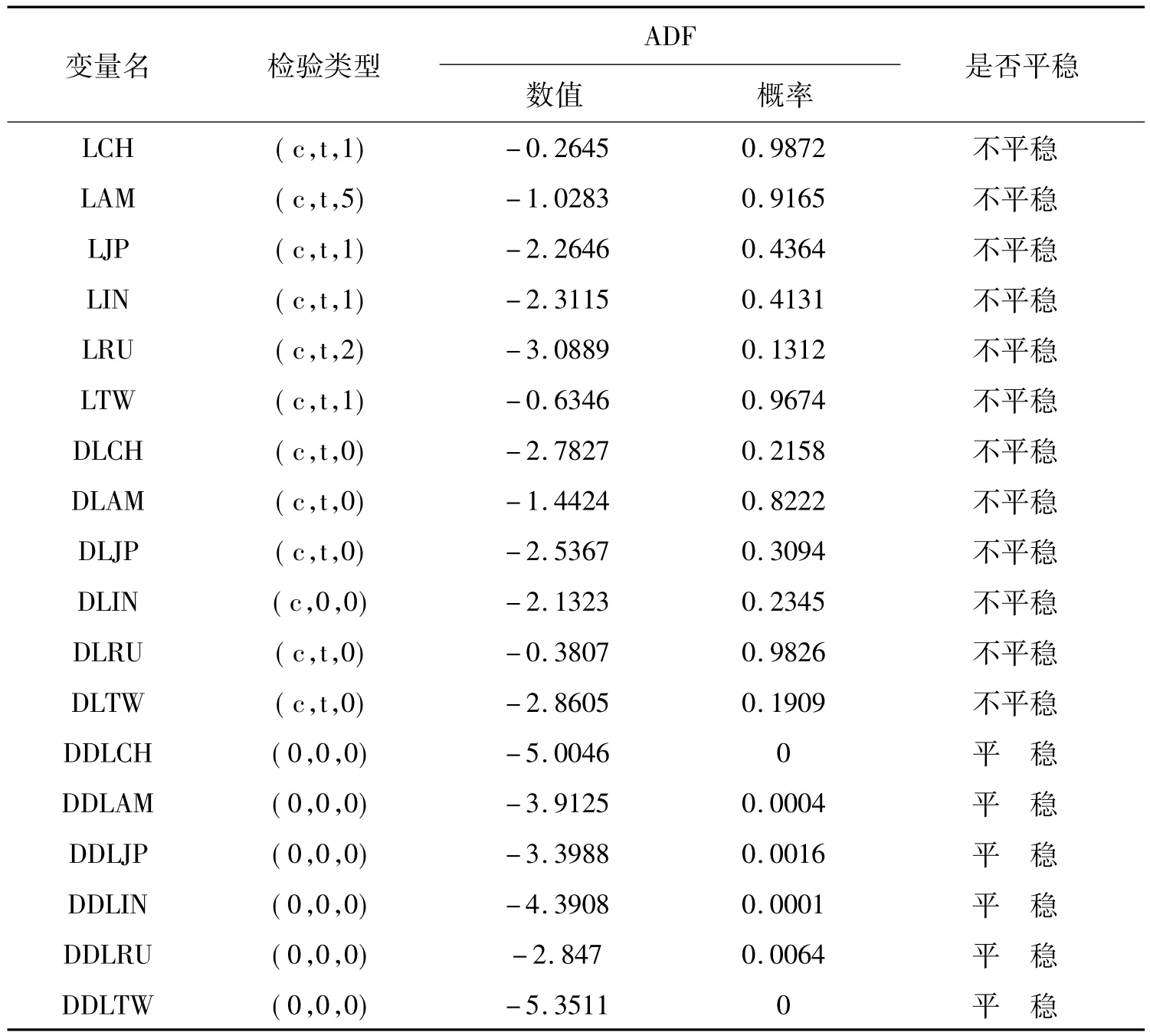
表1 国防实力的ADF单位根检验结果
通过ADF和PP单位根检验可以看出,中美日印俄和中国台湾的国防实力的原始值取对数之后均为二阶差分平稳序列,一阶差分后的序列均存在一个单位根,都为一阶单整序列I(1),从而说明各一阶差分后的序列(即国防实力的变化)可能存在协整关系,顾可做协整分析。本文采用Engle-Granger两步法进行了各国(地区)国防实力变化之间的协整分析①为消除序列相关性,在回归过程中采用了广义最小二乘法(GLS)。,变量DLCH分别对变量DLAM、DLJP、DLIN、DLRU和DLTW进行回归后的残差依次记为CH-AM、CH-JP、CH-IN、CH-RU 和 CH-TW,同理,可得到残差 AM-CH、AM-JP、AM-IN、AM-RU、AMTW、JP-CH、JP-AM、JP-IN、JP-RU、JP-TW、IN-CH、IN-AM、IN-JP、IN-RU、IN-TW、RU-CH、RU-AM、RU-JP、RU-IN、RU-TW、TW-CH、TW-AM、TW-JP、TW-IN 和 TWRU,总共得到30个残差,对这30个残差进行单位根检验,结果见表3①本文只给出PP检验结果,ADF检验得出与PP检验相同的结论。。
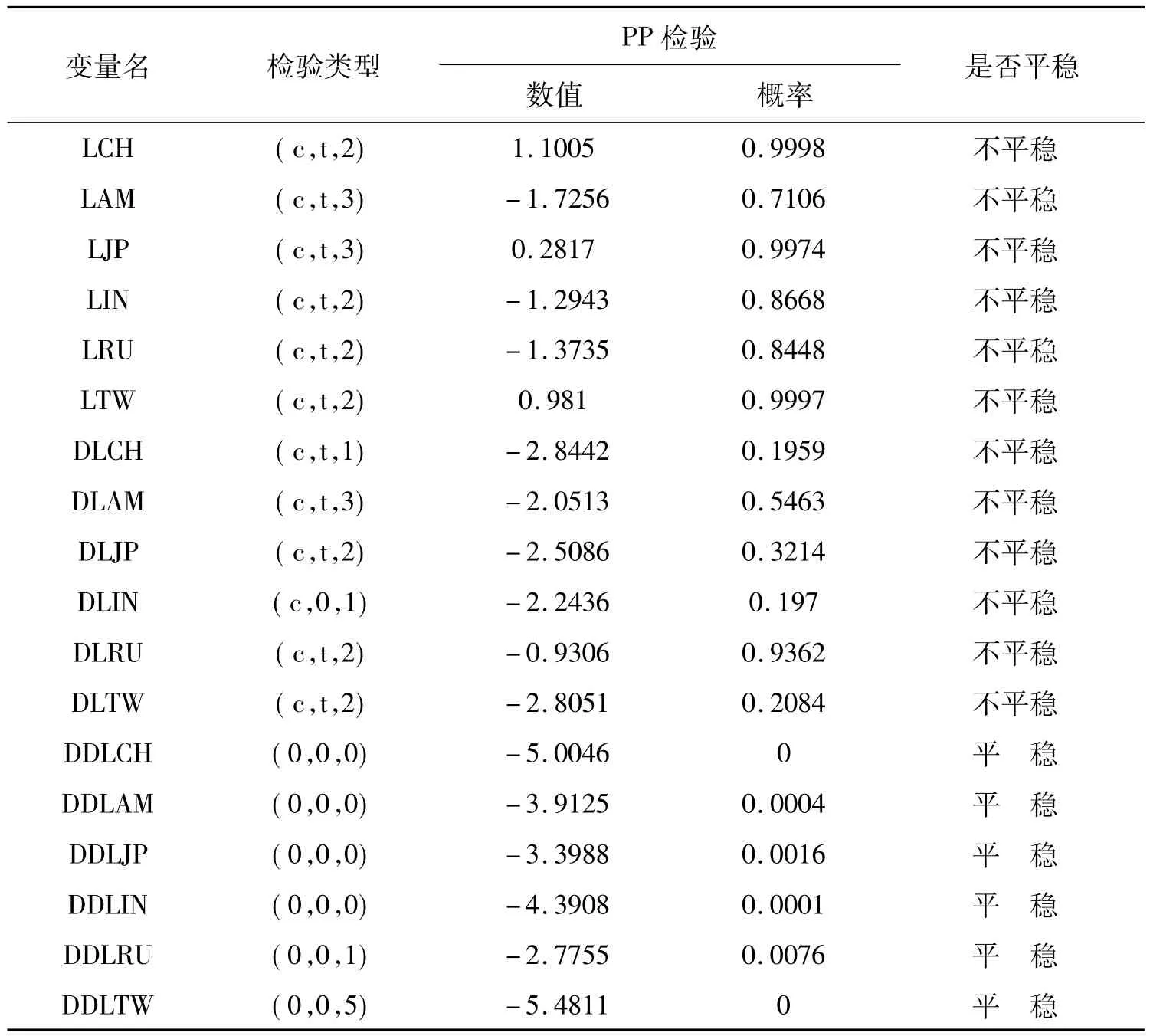
表2 国防实力的PP单位根检验结果
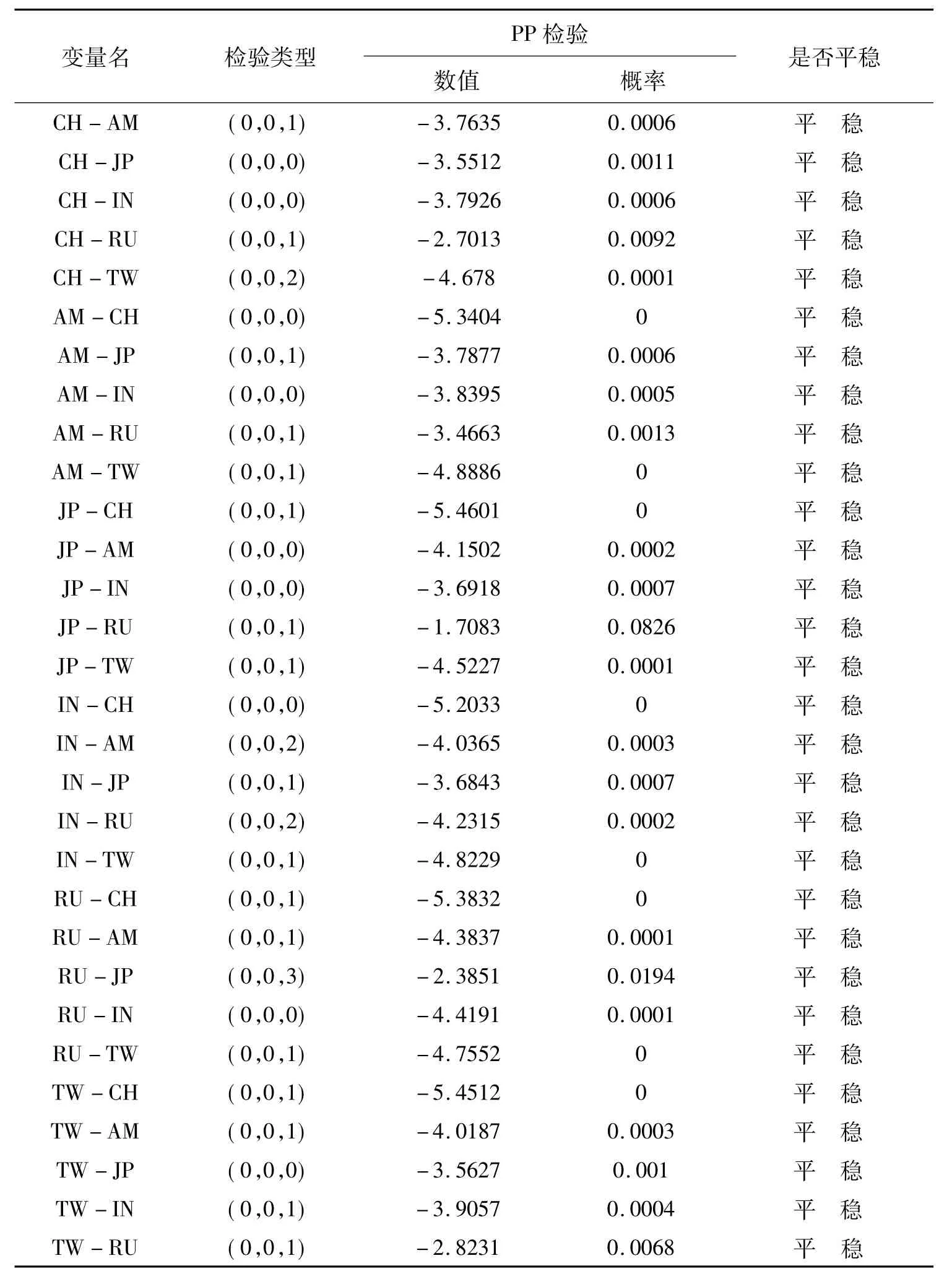
表3 残差的PP单位根检验结果
军备竞赛实证分析
根据以上假设条件和相关数据的分析,本文利用国防实力变化方面的有关数据,检验了中国、美国、日本、印度、俄罗斯和中国台湾之间的军备竞赛。从表1和表2中可以看出,DLCH、DLAM、DLJP、DLIN、DLRU和DLTW都是一阶单整序列,表3表明这些变量相互之间存在协整关系,因而可以建立回归方程。由于数据的缺乏以及苏联解体等实际情况,本文没有考虑苏联解体之前的情况,只分析了1990年以后俄罗斯的军备竞赛情况,回归结果见表4①为消除序列相关性,在回归过程中采用了广义最小二乘法(GLS)。。
由于是时间序列,每个回归方程的拟合度都很高,R2和调整后的R2都在0.6以上,DW值在1.8—2.2之间。在DLRU2(1990年以后俄罗斯国防实力取对数之后的一阶差分数据)对DLJP的回归方程中②1979—1990年前苏联的国防实力与1990年后俄罗斯的国防实力相比,发生了较大转折,为了保持数据的一致性,本文只考虑1990年后俄罗斯的国防实力(DLRU2)。其中,DLRU2和其他变量之间也存在协整关系。,结果对时间的选取比较敏感,为便于比较,本文列出了两个回归结果,其中当采用1991—2004年数据时③之所以没有采用2005年的数据是因为2005年数据产生较强的序列相关性。,回归得到的系数为-0.4201,但这个系数并不显著。当采用1990—2004年数据时,系数为1.6182,并在1%的显著性水平下拒绝了原假设。
由表4可以看出,1990—2004年期间,在日本和俄罗斯之间的回归方程中,回归系数均为正,且十分显著,进而表明在这段期间日本和俄罗斯之间很可能存在军备竞赛,但是若采用1991—2004年的数据,只能得出日本会随着俄罗斯国防实力的增加而增加本国国防实力的结论,并不能得出俄罗斯会随着日本国防实力的增加而增加本国国防实力的结论,进而表明1991—2004年期间日本和俄罗斯之间不存在军备竞赛。可见,日本和俄罗斯之间是否存在军备竞赛和样本的选取有很大关系。
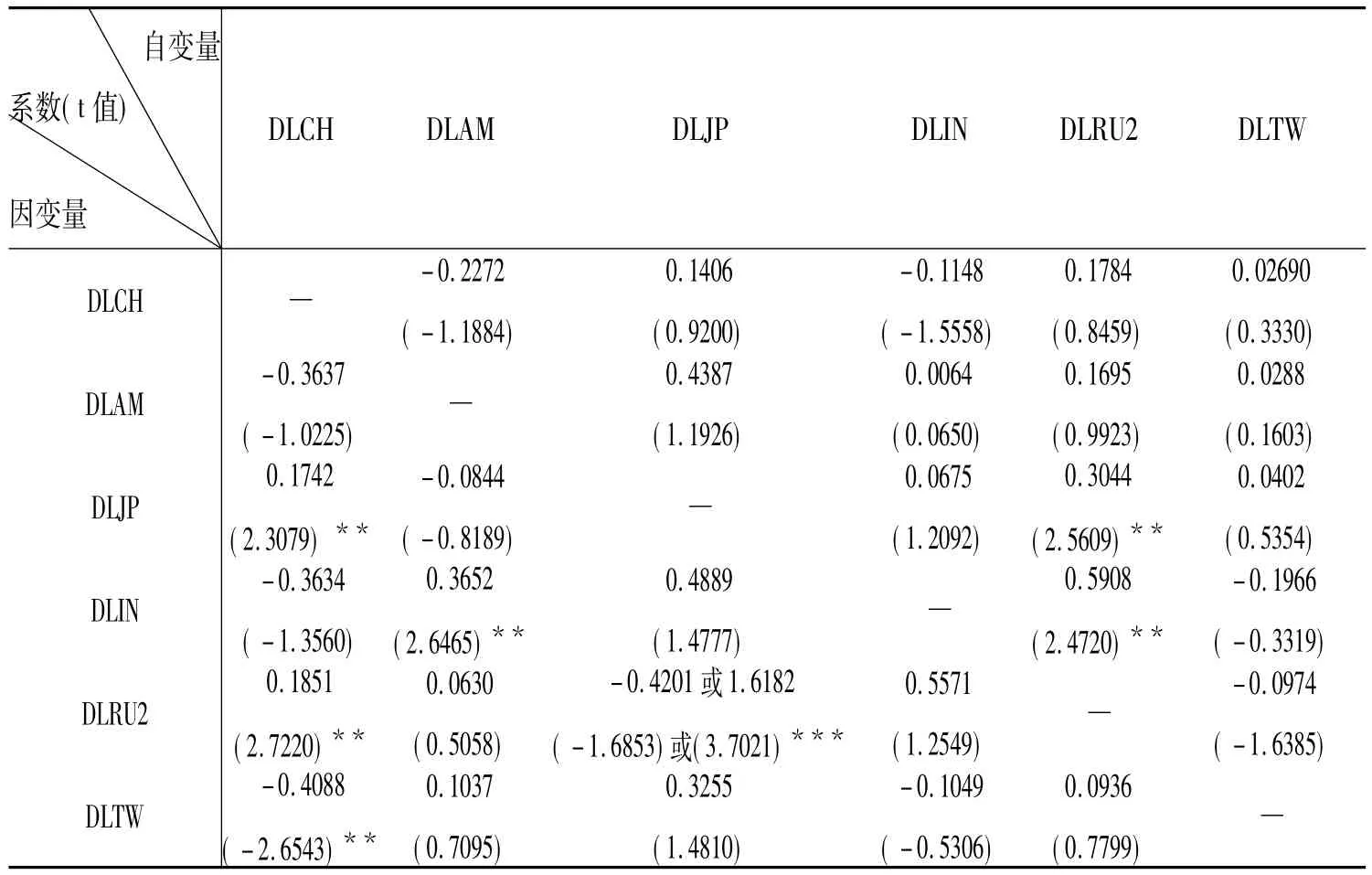
表4 中美日印俄和中国台湾军备竞赛分析
表4中的回归结果表明,除了日本和俄罗斯之间可能存在军备竞赛外,其他国家以及中国台湾之间没有在国防实力方面相互攀比,竞相增加国防实力,并不存在军备竞赛。但并不排除这段时期部分国家(地区)单方面根据对手的国防实力改变本国(地区)的国防实力,从表5中可以发现,日本和俄罗斯都会根据我国国防实力的情况来改变本国的国防实力,由于回归系数都为正数并且比较显著,所以可以预见,当中国国防实力增加时,日本和俄罗斯的国防实力也会随之增加,但中国却没有因为日本和俄罗斯国防实力的增加而增加国防实力。可见,作为发展中国家的中国,坚定不移地走和平发展的道路,中国国防实力的增加仅仅是出于维护国家统一和领土完整等方面的需要,并不是为了与其他国家和地区进行军备竞赛,中国没有与其他国家和地区进行军备竞赛,也不会对其他国家和地区构成军事威胁,“中国军事威胁论”的观点并不成立。
值得一提的是,美国在这一时期成为唯一的军事大国,相对其他国家(地区)具有绝对的军事优势,所以美国并没有根据其他国家(地区)国防实力的情况来调整本国国防实力,而印度为了和美国等国家争夺在亚洲的军事地位,其国防实力会随着美国国防实力的调整做出相应变化。由表4还可以看出,虽然印度也会根据俄罗斯的国防实力情况进行调整,但这种调整并不是为了和俄罗斯进行军事竞争,而是由于俄罗斯是印度武器装备的主要进口国,当俄罗斯的国防实力雄厚时,印度便会有更多的机会从俄罗斯获得更多先进的武器装备。
研究进一步发现,中国台湾的国防实力会根据中国大陆国防实力的变化发生相应变化,但这种变化是反向变化,从而说明,中国大陆和中国台湾之间不仅不存在军备竞赛,中国台湾反而会从中国大陆国防实力中获得利益,存在“搭便车”的现象,中国大陆的国防实力不仅为大陆同时也为中国台湾提供了发展经济的安全环境。
为了进一步验证以上结论,本文采用了格兰杰因果检验进行了验证①本文只提供了有显著关系国家(地区)间格兰杰因果检验结果,没有显著关系国家之间不存在格兰杰因果关系。。结果如下:

表5 格兰杰因果检验结果
表4和表5的结论除了俄罗斯和印度之间的关系不一致外,其余基本一致。表5的结果显示俄罗斯国防实力的变化能引起印度国防实力的变化,而在表4中却不能得出类似的结论。表4的结果表明印度和俄罗斯的国防实力变化之间并不存在格兰杰因果关系,但显示日本和俄罗斯的国防实力变化存在双向因果关系,从而说明日本和俄罗斯之间很可能存在军备竞赛。为进一步验证这种结论,并得出军备竞赛的稳定状态,本文采用了理查森军备竞赛模型进行了验证。
理查森模型可以用国防实力的变化来表示①姜鲁鸣主编.现代国防经济学.中国财政经济出版社,2007,令m(t)表示甲国的国防实力,n(t)表示乙国的国防实力,dm/dt和dn/dt分别表示m(t)和n(t)的变化率。dm/dt(dn/dt)取决于三个独立的因素:第一个因素称为防务因素,即乙国(甲国)的国防实力n(t)(m(t)),敌对国的国防实力对本国国防实力的变化率具有正向关系,表示保卫自己抵抗对手的需要;第二个因素是疲劳因素,即甲国(乙国)国防实力m(t)(n(t)),该因素对dm/dt(dn/dt)具有负向影响;第三个因素称为委屈因素,表示所有影响dm/dt(dn/dt)的其他因素。那么理查森模型可表示为:

其中,g和h表示委屈项,其符号可正可负,k、α、L、β均为正数。在一个动态过程的均衡点上,国防实力的变化率为0,即dm/dt=dn/dt=0时,从而得到甲国对乙国的反应函数:和乙国对甲国的反应函数:见图1。利用以上两个反应函数可以得出:如果g和h均为正数,且αβ-LK>0,则存在一个均衡点(点A),也就是说军备竞赛存在稳定状态,而不至于无限持续下去并最终爆发战争。在稳定状态下,甲国和乙国的国防实力分别为:
采用ADF和PP单位根方法可以验证1991—2004年间序列DLJP和DLRU2以及序列LJP和LRU2(1990年以后俄罗斯国防实力取对数之后的数据)均为一阶单整序列,采用Engle-Granger两步法检验发现DLJP与LRU2、LJP之间以及DLRU2与LJP、LRU2之间存在协整关系,故可以建立如下理查森竞赛模型①之所以没有采用2005年的数据是因为2005年数据产生较强的序列相关性。1990—2004年的数据与1991—2004年的数据得出的结论一致。:
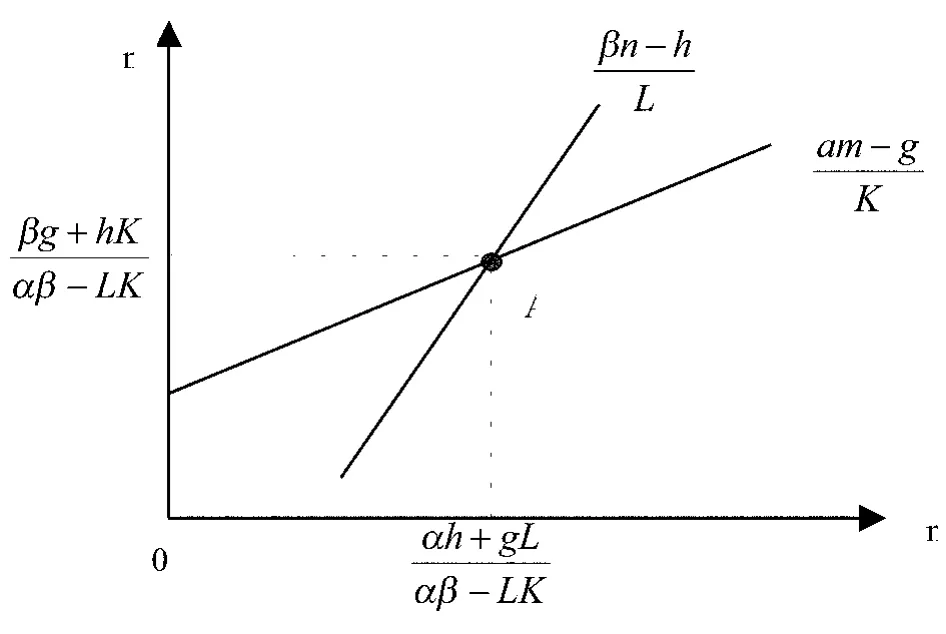
图1 两国国防实力之间的反应函数图

括号内的数值为t值,通过t值可知所有变量和常数前的系数均不等于0。与理查森理论模型比较,发现除了方程(3)中LJP前的系数符号为负外,其余变量前的系数符号均符合理查森模型的假设。但由于LJP前的系数符号为负,说明日本国防实力的增加不能引起俄罗斯国防实力的增加,也就说明他们之间不存在军备竞赛。我们可以把条件放宽,即允许LJP前的系数符号为负,由于g=1.2837和 h=1.8815 均为正数,αβ -LK=( -0.2178) ×( -0.02212) -( -0.2732) ×0.02112=0.01059 >0,所以即便日本和俄罗斯之间存在军备竞赛,也会达到一种稳定的状态,而不会持续进行下去。可以验证,在稳定状态下,日本和俄罗斯的国防实力均为正数。
结果与讨论
本文采用中国、美国、日本、印度、俄罗斯和中国台湾1979—2005年的国防实力数据,建立了理查森军备竞赛模型、协整模型和格兰杰因果检验模型,分析了20世纪80年代以来的中国、美国、日本、印度、俄罗斯和中国台湾之间的军备竞赛问题。研究发现,除了俄罗斯和日本可能存在军备竞赛外,其他国家以及中国台湾之间并不存在军备竞赛的迹象,国际环境整体比较安全,但这并不能排除部分国家(地区)单方面根据对手的国防实力情况来改变本国(地区)的国防实力,例如,日本和俄罗斯都会根据我国国防实力的情况来改变本国的国防实力,当中国国防实力增加时,日本和俄罗斯的国防实力也会随之增加,但中国却没有因为日本和俄罗斯国防实力的增加而增加国防实力。可见,中国坚定不移地走和平发展道路,并没有搞军事扩张和军备竞赛,不会对其他国家和地区国家构成军事威胁,“中国军事威胁论”的观点并不成立,现阶段我国积极推进国防现代化并非是出于军备竞赛的考虑,而是适应世界新军事变革发展的趋势,也是维护国家安全和发展利益以及维护祖国统一和领土完整的需要。而印度为了争当世界军事强国,和美国等国家争夺在亚洲的军事地位,以便保持和发展一支地区进攻性军事力量,其国防实力随着美国国防实力的调整做出相应变化。中国台湾的国防实力会根据中国大陆国防实力的变化发生反向变化,从而说明中国大陆和中国台湾之间不仅不存在军备竞赛,中国台湾反而从中国大陆国防实力中获得利益,存在“搭便车”现象,中国大陆的国防实力不仅为大陆同时也为中国台湾提供了发展经济的安全环境。
总体而言,我国经济建设的外部环境相对稳定,短时间内不会存在军备竞赛和大规模战争,因而,我国仍然要以经济建设为中心,转变经济发展方式,继续保持经济又好又快发展。但同时也要看到,我国仍然和印度、日本等国家存在领土和领海争端,还是当今世界唯一一个没有实现统一的大国,为了维护国家安全和发展利益以及维护祖国统一和领土完整,我国需要继续坚持防御性的国防政策,在经济不断发展的基础之上,逐步提高我国国防实力,建设与大国地位相称、与国家安全和发展利益相适应的强大国防力量。

