低噪声深沟球轴承仿真分析
孙朝阳,杨海生,梁英,邓四二
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.洛阳LYC轴承有限公司,河南 洛阳 471039)
符号说明
Cr——额定动载荷,N
Dpw——球组节圆直径,mm
Dw——钢球直径,mm
e——保持架偏心距,mm
fi,fe——内、外沟曲率半径系数
Fcj——钢球离心力,N
FDj——油气混合物对钢球阻力,N
Fr,Fa——轴承承受的外部径向、轴向载荷,N
FRij,FRej——钢球与内、外沟道接触入口区流-体动压摩擦力,N
Jb——钢球转动惯量,kg/mm2
Jc——保持架转动惯量,kg/mm2
mb,mc,mi——钢球、保持架、内圈质量,kg
ni——内圈转速,r/min
PRj,PSj——钢球与兜孔接触入口区之间滚动、滑动摩擦力,N
Qcj——第j个钢球与兜孔间作用力,N
Qij,Qej——钢球与内、外沟道间法向接触力,N
Tij,Tej——钢球与内、外沟道间的拖动力,N
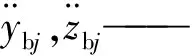

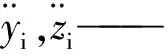
Z——钢球数
βj——钢球与兜孔作用力夹角,(°)
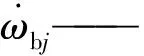
ωc,ωi——保持架、内圈角速度,rad/s

ψj——第j个钢球方位角,(°)
Δbj——第j个钢球相对兜孔中心在径向平面的位移,mm
低噪声深沟球轴承[1]主要应用于精密机械和高档家用电器。目前, 日本NSK已经推出了“静音”与“超静音”轴承[2], 其技术处于国际领先水平。轴承噪声基本上是由轴承在运转过程中产生的振动经过空气等介质的传播引起的,因此,控制噪声需从降低振动着手。国内、外已有众多学者从结构设计着手去研究球轴承振动的规律。文献[3]研究了径向游隙对滚动轴承振动的影响规律;文献[4]研究了钢球个数以及轴承预紧力对球轴承振动的影响;文献[5-6]研究了波纹度对球轴承振动的影响;文献[7]研究了浪形保持架兜孔几何参数对球轴承振动的影响;文献[8]研究了摩擦学因素对球轴承振动的影响规律;文献[9]研究了深沟球轴承噪声寿命与预载荷的关系,认为当噪声寿命要求超过10 000 h时,预紧力取(0.005~0.01)Cr为宜。但是,这些研究没有全方位阐述球轴承振动的规律,尤其在保持架的结构设计方面,目前国内主要靠经验来进行。
文中以低噪声深沟球轴承为研究对象,在深沟球轴承动力学分析的基础上[10-12],建立低噪声深沟球轴承动态性能仿真数学模型,利用ADAMS[13]多体动力学分析软件,开发了低噪声深沟球轴承仿真分析软件,对低噪声深沟球轴承进行了实例仿真分析,以探究各个参数对轴承振动的影响规律。
1 球轴承动力学振动数学模型
1.1 钢球的动力学平衡方程
对于低噪声深沟球轴承,轴承外圈固定,内圈以恒定转速ni旋转,保持架由钢球引导,若轴向载荷Fa=0,则钢球与内、外套圈之间的接触角可假定为零。
在纯径向力作用下,钢球在径向平面受力如图1所示,忽略重力的影响,则钢球的动力学平衡方程由两个力平衡方程和一个力矩平衡方程组成,方程如下
(1)
(2)
(3)
式中:下标j为钢球序号,j=1,…,Z。
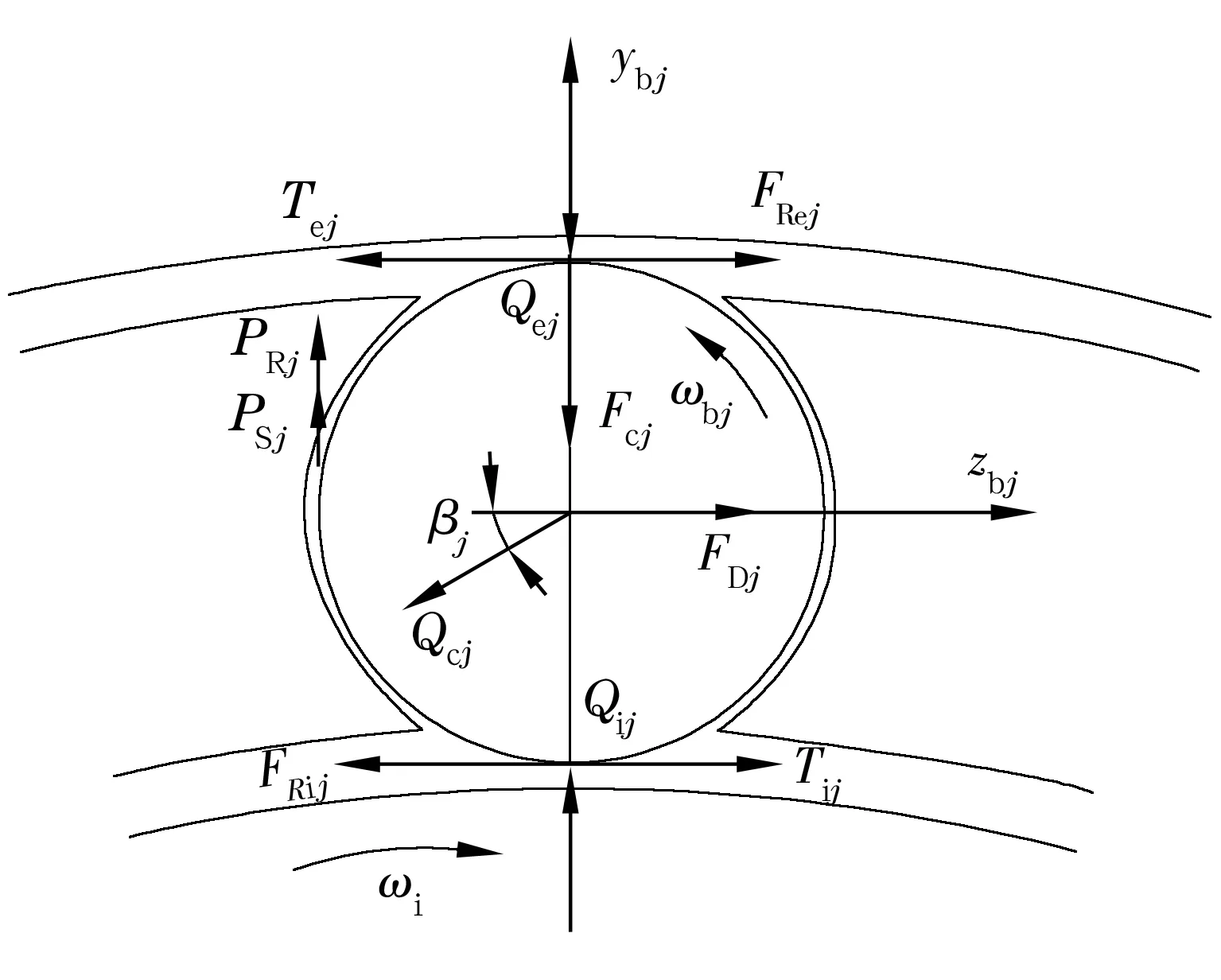
图1 第j个钢球受力示意图
1.2 保持架的动力学平衡方程
低噪声深沟球轴承保持架引导方式一般为钢球引导。图2是保持架第j个兜孔与钢球之间作用力示意图。考虑一个兜孔,保持架受到如下力和力矩的作用
Fyj=(PRj+RSj-Qcjsinβj)cosψj-Qcj·
cosβjsinψj,
(4)
Fzj=(PRj+PSj-Qcjsinβj)sinψj+Qcjcosβj·
cosψj,
(5)
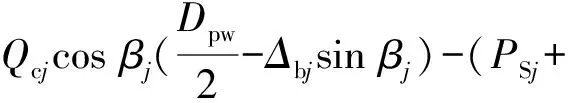
(6)
考虑全部兜孔所受的力和力矩,可以得到保持架的平衡方程为
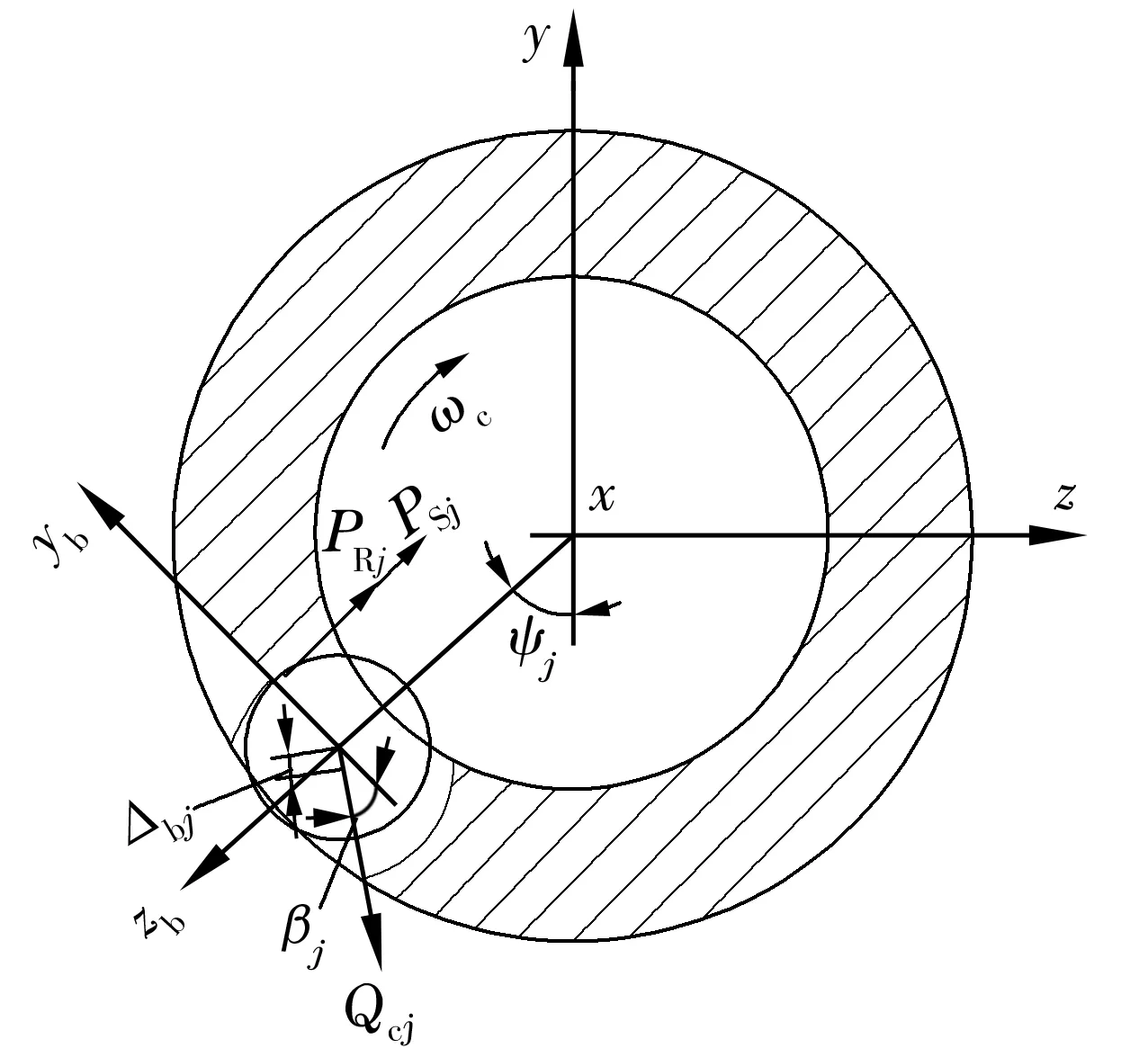
图2 保持架第j个兜孔与钢球之间作用力示意图
(7)
(8)
(9)
1.3 内圈的动力学平衡方程
内圈与第j个钢球之间作用力示意图如图3所示,内圈的动力学平衡方程为
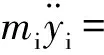
Qijcosψj],
(10)
(11)

图3 内圈与第j个钢球之间作用力示意图
上述各式中力的计算方法详见文献[12]。迭代求解时,需将内圈、钢球和保持架的动力学平衡方程联立求解。
2 仿真结果与分析
以ADAMS多体动力学分析软件为平台,通过建立低噪声深沟球轴承动态性能仿真数学模型,开发出低噪声深沟球轴承仿真分析软件,并以6205型低噪声深沟球轴承为例(轴承具体参数见表1)进行了实例分析。该轴承保持架为冲压浪形保持架,材料为SPCC。

表1 轴承主参数
假定轴承在20 ℃下工作,外圈固定,内圈转速ni=11 000 r/min,径向载荷Fr=1 200 N,轴向载荷Fa=0 N,取内圈质心径向振动加速度级来描述整个轴承的振动水平。
2.1 径向游隙对轴承振动的影响
图4是在0组径向游隙范围内,通过改变轴承径向游隙,轴承振动的变化情况。
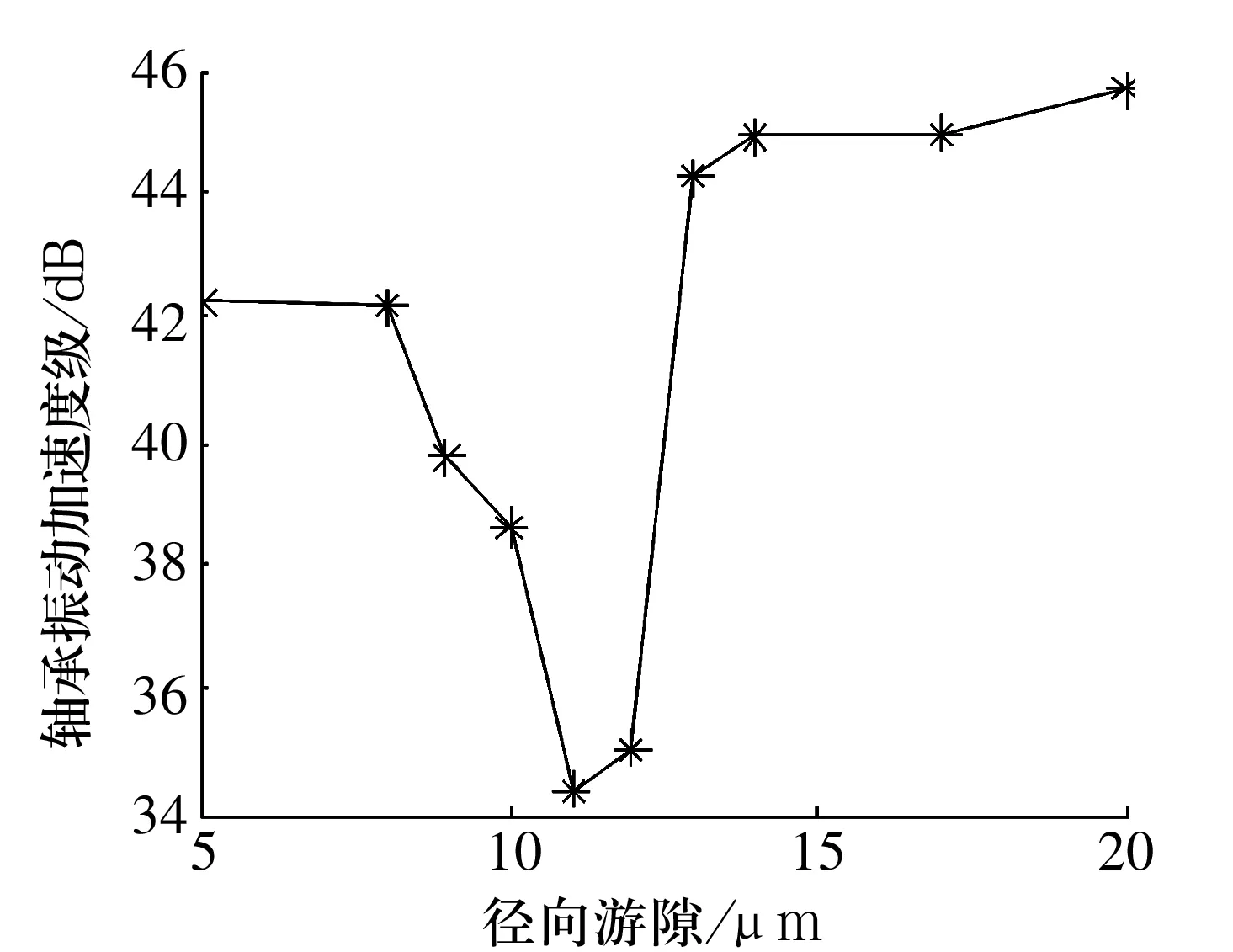
图4 径向游隙对轴承振动的影响
由图4可以看出,径向游隙对轴承振动的影响很大,且是非线性的,随着径向游隙从5 μm变化到20 μm,轴承的振动呈现出先减小后增大的趋势。当径向游隙取11μm时,轴承的振动最小。
2.2 内、外沟曲率半径对轴承振动的影响
图5为径向游隙11 μm时,内、外沟曲率半径对轴承振动的影响情况。
图5a为fe=0.525时,轴承的振动随fi的变化规律,可以看出当fi=0.510 9时轴承的振动最小;图5b是fi=0.515时, 轴承的振动随fe的变化规律,可以看出当fe=0.527 2时,轴承的振动最小。
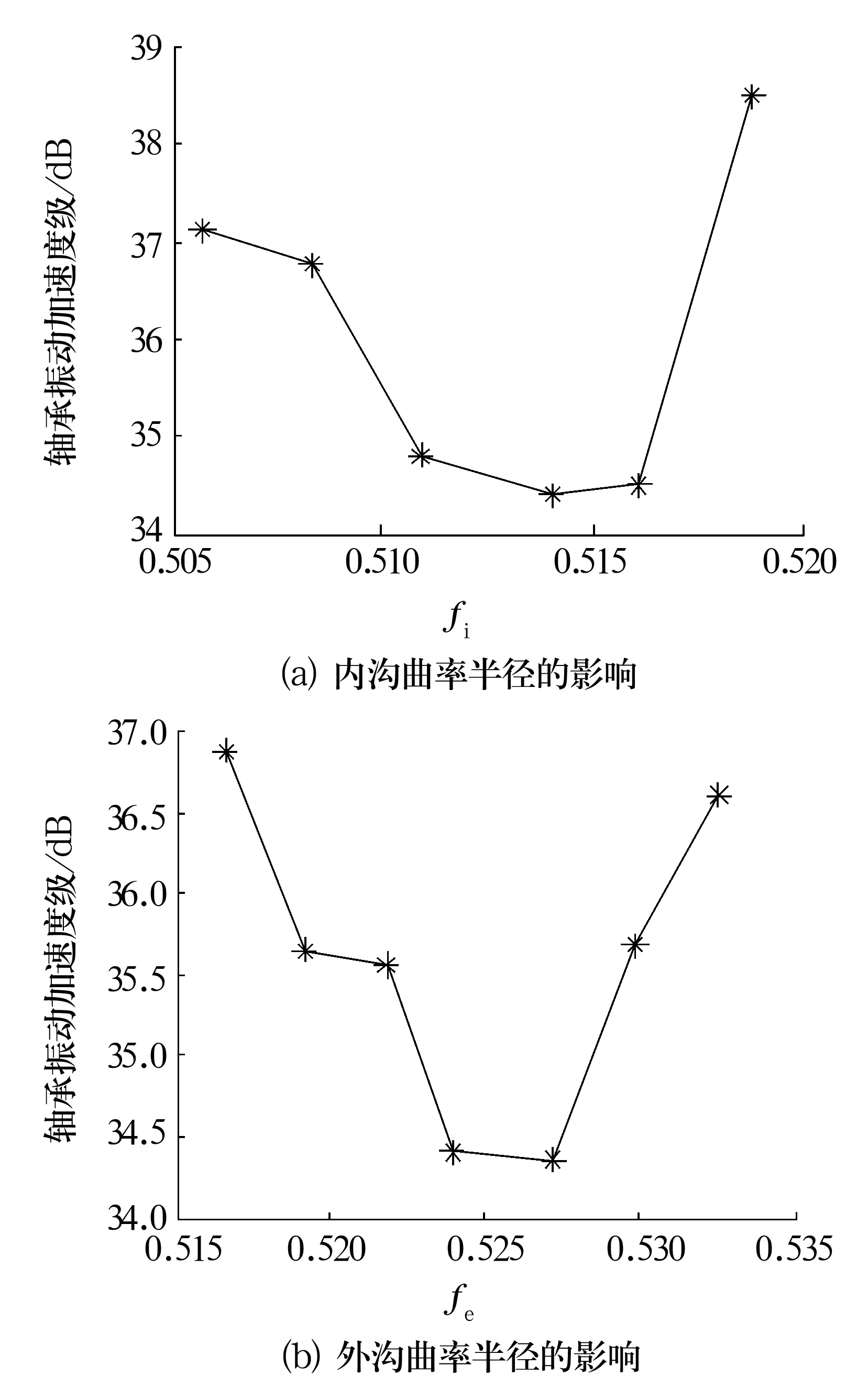
图5 内、外沟曲率半径对振动的影响
2.3 保持架结构参数对轴承振动的影响
图6为径向游隙11 μm时,保持架结构参数对振动的影响规律。
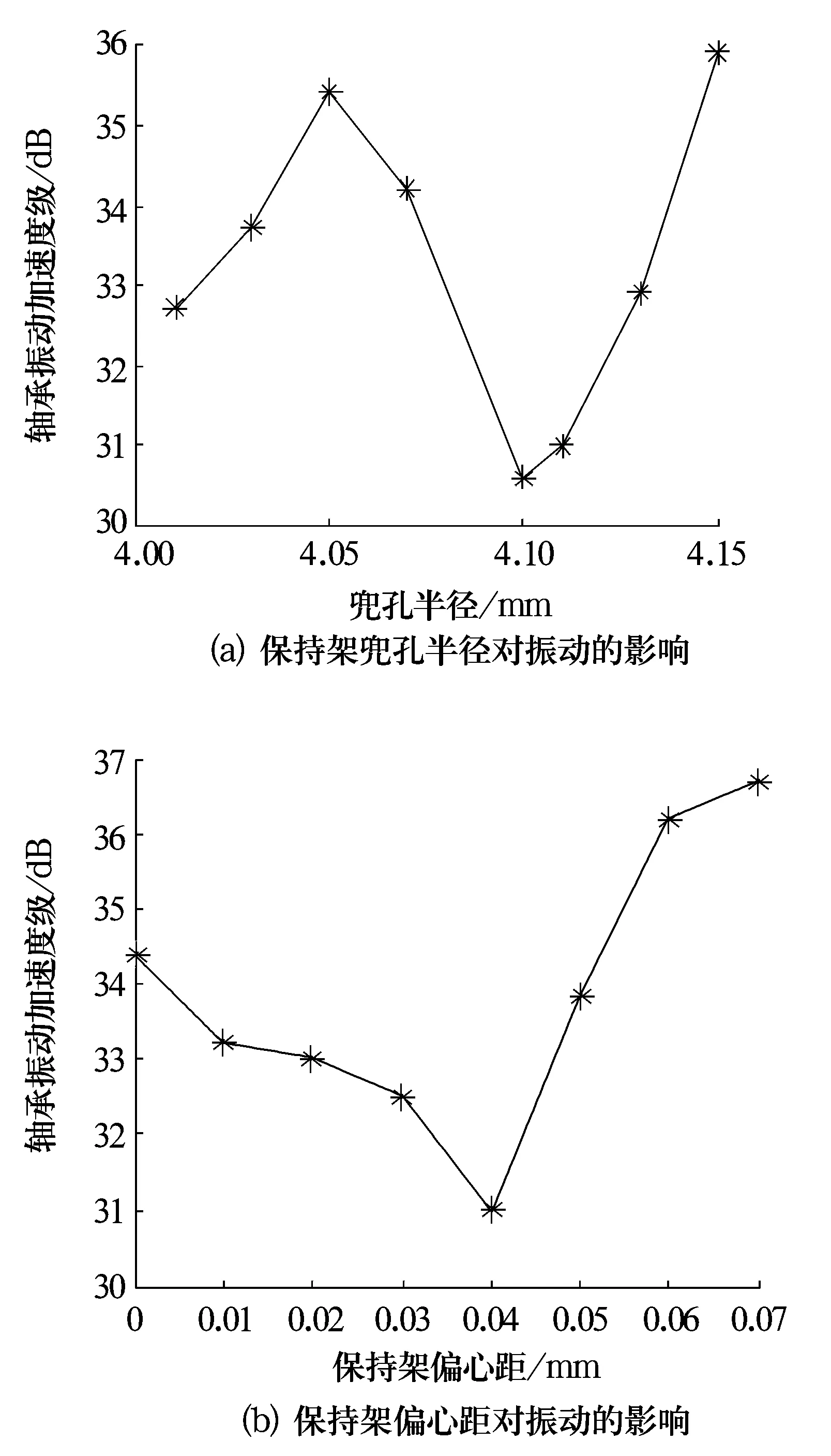
图6 保持架结构参数对振动的影响
由图6a可以看出,随着保持架兜孔半径的增大,轴承的振动呈现先增大后减小再增大的趋势。当兜孔半径为4.1 mm时,轴承振动最小。这是由于兜孔较小时润滑剂不足,钢球与兜孔碰撞频繁导致振动较大;兜孔半径超过某个值后,由于钢球与兜孔间隙过大,振动呈现增长趋势;因此,兜孔半径应取值恰当。由图6b可以看出,随着保持架偏心距e的增大,轴承的振动呈现先减小后增大的趋势。当偏心距e=0.04 mm时,轴承振动最小。
2.4 轴向力对轴承振动的影响
图7和图8为ni=11 000 r/min,Fr=1 200 N,径向游隙为11 μm时,轴向载荷Fa对轴承振动以及寿命的影响情况。

轴向载荷与额定动载荷的比值/%
轴向载荷与额定动载荷的比值/%
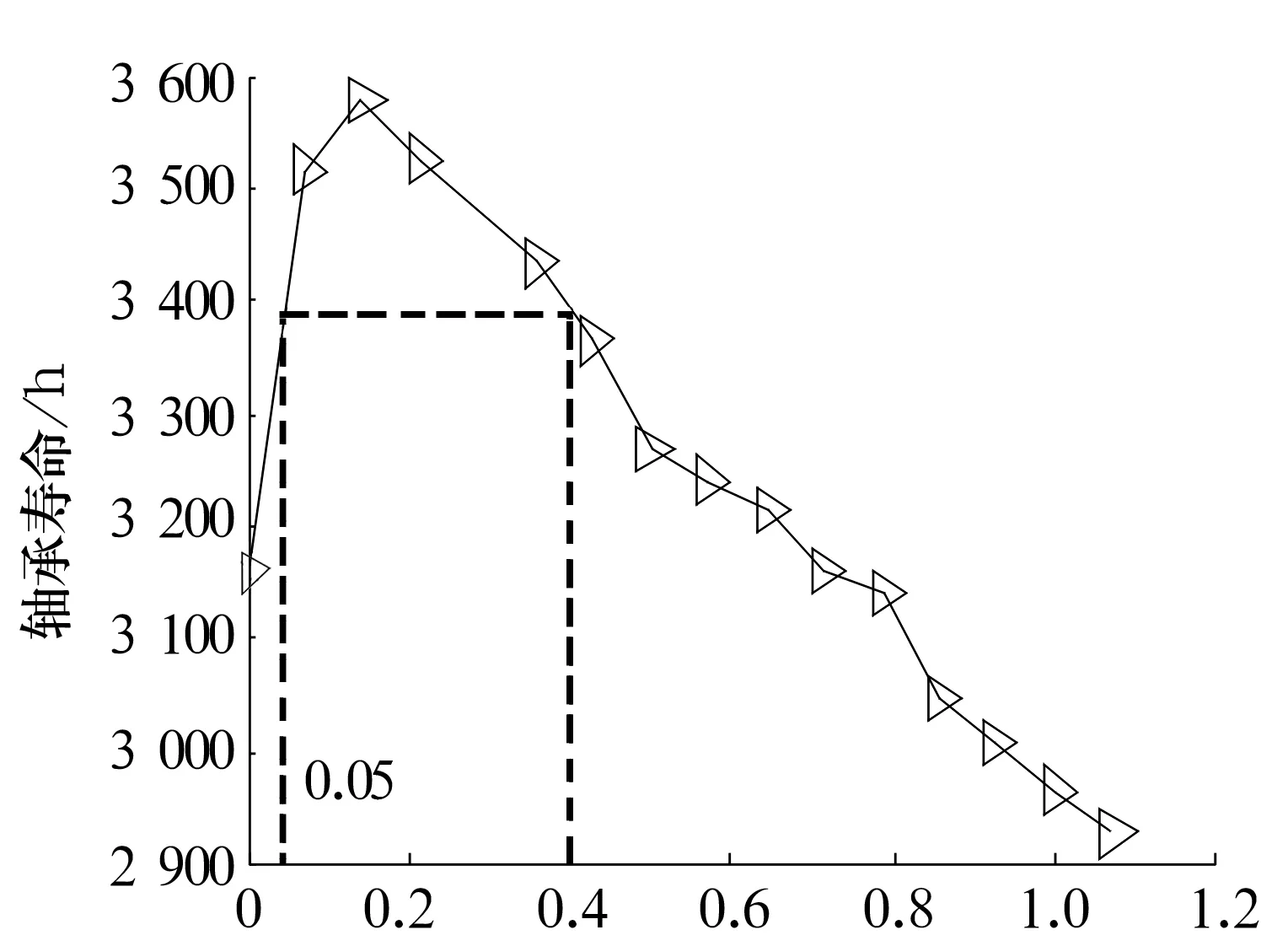
由图7可以看出,对深沟球轴承施加一定的轴向载荷可以有效减小振动,当0.53%≤Fa/Cr≤0.89%时,减振效果最为明显。由图8可以看出,当0.05%≤Fa/Cr≤0.4%时,可以有效提高轴承的寿命。
2.5 工况参数对轴承振动的影响
表2给出了ni=11 000 r/min,Fa=0 N,径向游隙为14 μm时,轴承振动随径向力的变化情况。由表2知,Fr=1 400 N时,轴承振动较小。

表2 不同径向力下的振动值
表3给出了Fr=1 200 N,Fa=0 N,径向游隙为14 μm时,轴承振动随转速的变化情况。由表3知,当ni=10 000 r/min时,轴承振动较小。
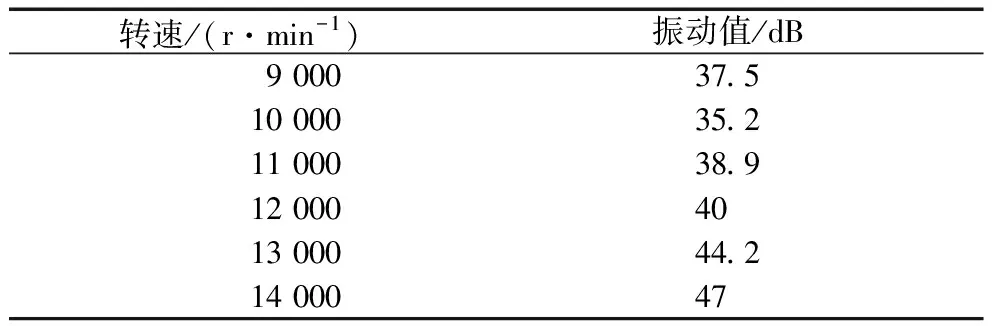
表3 不同转速下的振动值
3 结束语
(1) 轴承径向游隙及内、外沟曲率半径等结构主参数对轴承本底振动值影响很大,需要合理选择。
(2) 保持架兜孔半径大小与轴承振动值呈非线性关系,存在一个合理的兜孔半径,使得轴承振动值最小。
(3) 保持架兜孔形状对轴承振动有一定的影响,具有一定偏心距的椭球形兜孔有利于降低轴承振动值。
(4) 对低噪声深沟球轴承施加一定的轴向载荷,可以降低轴承的振动值,所加轴向载荷一般取(0.53%~0.89%)Cr为宜。
(5) 对低噪声深沟球轴承施加一定的轴向载荷,可提高轴承的寿命,所加轴向载荷一般取(0.05%~0.4%)Cr为宜。
(6) 轴承振动大小与轴承工况条件有关,设计轴承时应根据具体工况条件,综合考虑轴承振动值与轴承寿命两个指标,选取合适的轴承结构参数。

