球笼式等速万向节轴向间隙形成的周向间隙分析

刘庭洋，郭常宁，石宝枢，杨洪兴

(1.上海交通大学 机械与动力工程学院，上海 200240；2.浙江众达传动股份有限公司，浙江 金华 321025)

球笼式等速万向节是前轮驱动轿车的关键部件之一，其可以实现成夹角的输入轴与输出轴的等角速度传动。然而由于运动副配合需要[1]及其制造和装配等方面的原因，其各零件之间存在间隙，其中轴向间隙以及由其形成的周向间隙是造成万向节内部各零件窜动与冲击以及使用寿命降低的重要原因。文献[2]对三球销式等速万向节周向间隙的计算公式进行了推导，给出了分析周向间隙的基本方法；文献[3]对球笼式等速万向节周向间隙进行了研究，分析了在给定制造误差条件下周向间隙的变化规律；但这些研究均未涉及轴向间隙形成周向间隙的条件及计算方法。在此，针对球笼式等速万向节的结构和运动形式，计算了任意摆角和转角下轴向间隙形成的周向间隙，并分析了周向间隙随摆角和转角的变化规律。

1 球笼式等速万向节的结构

图1为摆角为0时球笼式等速万向节的纵截面图和横截面图。球笼式等速万向节由钟形壳、星形套、保持架和6个均布钢球构成。钟形壳和星形套上各有6条半双心弧沟道。星形套、钟形壳沟道曲率中心A和B等距地偏置在万向节传动中心O的两侧，偏心距为e；钢球1的球心C在星形套中绕着A做圆周回转运动，其回转半径为R；6个钢球由保持架约束，其球心均在D-D平面内。球笼式等速万向节有两组绕O点转动的球面副：一组为星形套外球面与保持架内球面组成的球面副，另一组为钟形壳内球面与保持架外球面组成的球面副。

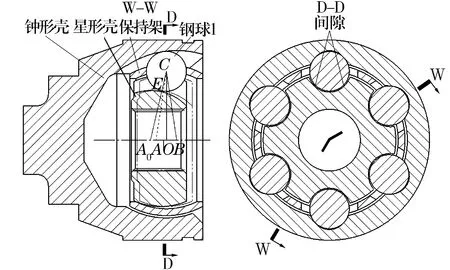
图1 周向间隙的形成

如图1所示，星形套初始时位于虚线位置，其球面中心与钟形壳及保持架球面中心重合于O点，钢球1与星形套沟道接触于E点。由于在星形套外球面与保持架内球面间存在径向间隙[4]，假设钟形壳和保持架不动，星形套可在E点与钢球1脱离接触，沿OA方向移动到实线位置，此时星形套外球面碰到保持架内球面，星形套沟道曲率中心也由A点移动到A0点。星形套沿OA方向移动的最大位移即为星形套与保持架间的轴向间隙δt(δt=AA0)。显然星形套移动时未与6个钢球发生干涉。星形套移动后，钢球与星形套沟道之间形成了周向间隙，星形套就可以相对转动。

钟形壳不动，星形套由虚线位置沿AO方向移动，显然星形套会与6个钢球保持接触，推动钢球和保持架一起移动，直至保持架外球面碰到钟形壳内球面为止。星形套沿AO方向移动的最大位移即为钟形壳与保持架间的轴向间隙δk，星形套移动后钟形壳与钢球之间同样形成了周向间隙。形成周向间隙的方式可分为钟形壳固定不动，星形套移动；或星形套固定不动，钟形壳移动，星形套或钟形壳移动时都只能沿其轴线方向移动。

2 空间坐标系的建立

为了便于计算和分析需建立空间坐标系，作如下假设：(1)钟形壳、星形套的双心弧沟道为理想沟道，不存在制造误差；(2)假设钟形壳不能摆动，星形套可上下摆动，其他情况可类似推导。

如图2所示，C点为钢球1既未摆动又未转动时的球心位置，此时，星形套、保持架及钟形壳三者的轴线重合于轴Ⅰ，钢球1摆动α角后球心由C点摆到了C0点位置，保持架和星形套的轴线也分别绕O点摆到了轴Ⅱ及轴Ⅲ的位置，星形套沟道中心也由A点摆动到A1点，规定此时的摆动方向为正。

图2 空间坐标系

(1)

在△A1OC1中A1C1=R，经计算得

(2)

由(1)和(2)式得

(3)

(4)

3 α≠ 0时周向间隙的产生

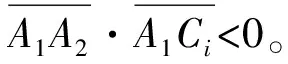
(5)

或

(6)

由图2知，第i+1个钢球的转角比第i个钢球的转角超前了60°，联系(3)式即可得φi+1=φi(β+60°)，所以万向节转动60°后min{φ1,φ2,φ3,φ4,φ5,φ6}变成了min{φ2,φ3,φ4,φ5,φ6,φ1}，即min{φi}以60°为一变化周期。

做出α>0时φ1随β的变化曲线可得

φ1<90°，β=0～60°，

(7)

做出α<0时φ3随β的变化曲线同样可得

φ3<90°，β=0～60°。

(8)

由(7)和(8)式可知，β=0～60°时，min{φi}<90°，由于min{φi}以60°为一变化周期，所以在任意α，β角下min{φi}<90°都成立，即(6)式恒不能满足。

当α>0，β=0～60°时，经比较可得max{φi}=max{φ3,φ4}。图3为α>0时φ3,φ4随β的变化曲线，图3中两条曲线的上半部分即为max{φi}。

图3 α>0时钢球3，4的φ角随β的变化曲线

由图3可知，φa=φ4(0)=φ1(180°)；φb=φ4(30°)=φ1(210°)。则α>0，β=0～60°时max{φi}<90°等价于

(9)

β*满足φ4(β*)=φ1(180°+β*)=90°，代入(3)式可得

(10)

类似可推导得max{φi}以60°为一周期，显然max{φi}关于α=0对称，这是由于万向节结构的对称性所致。根据max{φi}的变化特点联立(3)，(4)，(9)，(10)式得

(11)

或

(12)

设使(11)～(12)式成立的(α,β)属于集合Ω={(αk,βk)}，k=0，1,…,n。当m>0,(α,β)∈Ω时，(5)式成立，即星形套可沿OA1方向移动且不与6个钢球发生干涉，在星形套外球面碰到保持架内球面后不再移动。

当(α,β)不属于Ω或m<0,(α,β)∈Ω时，(5)～(6)式均不能成立，则星形套无论沿OA1或A1O方向移动至少会与一个钢球发生干涉，即星形套会带动此钢球一起移动，由于万向节摆动后钟形壳沟道与星形套沟道是空间交错的[5]，所以星形套推动钢球移动时，钢球又会与钟形壳沟道发生干涉，这就使得星形套实际上无法移动。总之，只有当(α,β)∈Ω时，星形套才能沿OA1方向移动。

用类似方法可推得，只有当(α,β)∈Ω时，钟形壳才能沿BO方向移动，直至钟形壳内球面碰到保持架外球面为止。

4 轴向间隙形成的周向间隙的计算

如图1所示，剖切线W-W与钢球1固连，万向节摆动α角转动β角后，剖切线W-W剖得的剖面Λ即为图4(图中钟形壳未画出)。O′y′z′面即位于面Λ上。设(α,β)∈Ω，如图5所示，星形套可沿OA1方向由虚线位置移动到相对于保持架的极限位置，相应地星形套沟道曲率中心A1移动到A3，星形套E端移动到E′位置，显然EE′//OA1。星形套与保持架间的轴向间隙δt=|EE′|。建立动坐标系O″x″y″z″，坐标原点O″位于A3点，x″轴与x′轴平行(未画出)，y″轴与直线A3C1重合，z″轴由右手定则产生，则O″x″y″z″坐标系可看作是O′x′y′z′坐标系沿z′轴平移位移d后，再绕移动后的x′轴旋转90°-γ2角后所得。

O″x″y″z″坐标系到O′x′y′z′坐标系的四阶变换矩阵为

(13)

式中：d=e+δt。

过点E，E′作垂线分别交轴Ⅲ于F，F′点。由几何关系可得

(14)

式中：Bt为星形套外球面中心至左端面的距离；Rt为星形套外球面径和保持架内球面径的公称值；εt为星形套与保持架间的径向间隙。

在△A1A3C1中，∠A3A1C1=180°-φ1，设A3C1=l，又A1C1=R，A1A3=δt，由余弦定理知

(15)

式中：l为星形套的沟道曲率中心与钢球球心的距离。

如图4所示，在O′y′z′坐标系中，线段A3C1与线段A1C1在y′轴上的投影相等，即

lsinγ2=Rsinφ1，

则

(16)

实际生产过程中一般使用周向间隙角来评价周向间隙的大小，周向间隙角等于周向间隙除以接触点到驱动轴线的距离。为了计算周向间隙角，应确定钢球哪个部位与星形套之间的间隙最小，作无数条平行于x′轴的直线分别交同一侧的钢球和星形套沟道于J1，K1，J2，K2，…，求得所有线段中|JK|的最小值即为钢球与星形套的最小间隙。如图4所示可用一个简便的方法来计算，过点A3作垂直于Λ面的剖面将钢球与星形套切成无数个面，计算出每个剖面上圆和双心弧的最小间隙，比较这些间隙值，最后得到钢球与星形套之间的最小间隙。根据星形套沟道的特点，可知过直线A3C1所做的剖面上，圆和双心弧的最小间隙即是钢球与星形套之间的最小间隙。

图4 轴向间隙的计算

沿直线A3C1作垂直于Λ平面的剖面φ1，如图5所示，钢球与星形套沟道在φ1面上的投影分别为圆1和双心弧1，圆1的圆心为C1，Q点为与双心弧1相切的圆的圆心。双心弧的沟道曲率半径为rs,双心弧沟道偏心距为es，钢球的半径为r。作平行于x″轴的直线分别交圆1和双心弧1于G′，G点和H，H′点，交y″轴于M点。

图5 圆和双心弧间的间隙示意图

由图5可知，圆1的方程为

x″2+(y″2-l)2=r2，

(17)

x″>0时，双心弧1的方程为

(18)

在O″x″y″坐标系中，设G点纵坐标为y″，由(17)～(18)式可得

(19)

令Δl=GH,由(19)式可得函数Δl为

(20)

对Δl求导

(21)

将(21)式代入(20)式，得最小间隙为

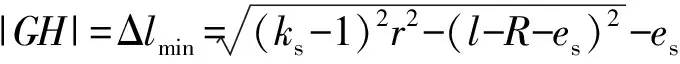
(22)

将(21)式代入(19)式可得G点在O″x″y″z″坐标系上的坐标为

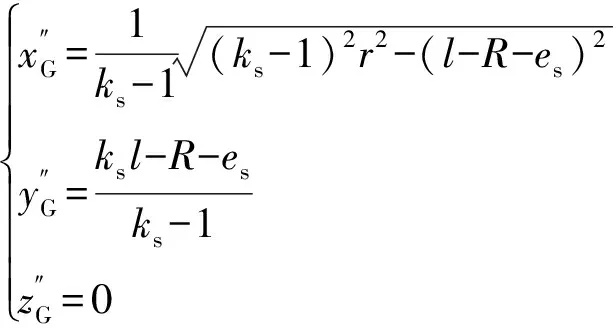
(23)

在图4中过点M作垂直于z′轴的剖面φ2，φ2面与z′轴交于N点，显然φ2面平行于O′x′y′面。由于直线HH′∥x′轴，所以直线HH′位于φ2面上，即点G，G′和点H，H′位于φ2面上，如图6所示。钢球与星形套沟道在φ2面中的投影分别为圆2、双心弧2，圆2的圆心为C7。线段GH的长度即是钢球与星形套的最小间隙，其局部放大图如图6b所示。

通过转换矩阵M将G点由O″x″y″z″坐标系转换到O′x′y′z′坐标系上，联立(13)，(16)，(23)式可解得G点在O′x′y′z′上的坐标为

(24)

(25)

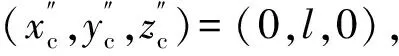
图6 圆和双心弧间的周向间隙计算示意图

(26)

由(24)～(26)式得

(27)

|GN|即为接触点G到星形套轴线的距离。在曲边△GPQ中，∠GQP=90°，∠HGP=ω1，∠HGQ=ω2，由余弦定理知|GQ|=|GH|cosω2=|GR|cos(ω2-ω1)，则钢球与星形套之间的周向间隙即弧长|GP|为

(28)

所以星形套与钢球之间的周向间隙角

(29)

5 计算示例与分析

现以星形套与钢球之间的周向间隙角θ1为例进行分析，钟形壳与钢球之间的周向间隙角可作类似分析。某球笼式等速万向节结构参数为：εt=0.07 mm，Rt=29.35 mm，Bt=10.3 mm，rs=9.08 mm，es=0.246 4 mm，r=8.731 5 mm，R=30.4 mm，e=4.5 mm。由(11)式可知，|α|<16.84°时轴向间隙与周向间隙存在，由(14)式可得轴向间隙δt=0.099 3；由(12)式知，16.84°<|α|<19.47°时，只有在β位于某些区间时轴向间隙与周向间隙存在，随着|α|的增大，这些区间逐渐变小，当|α|>19.47°时轴向间隙与周向间隙均不存在。

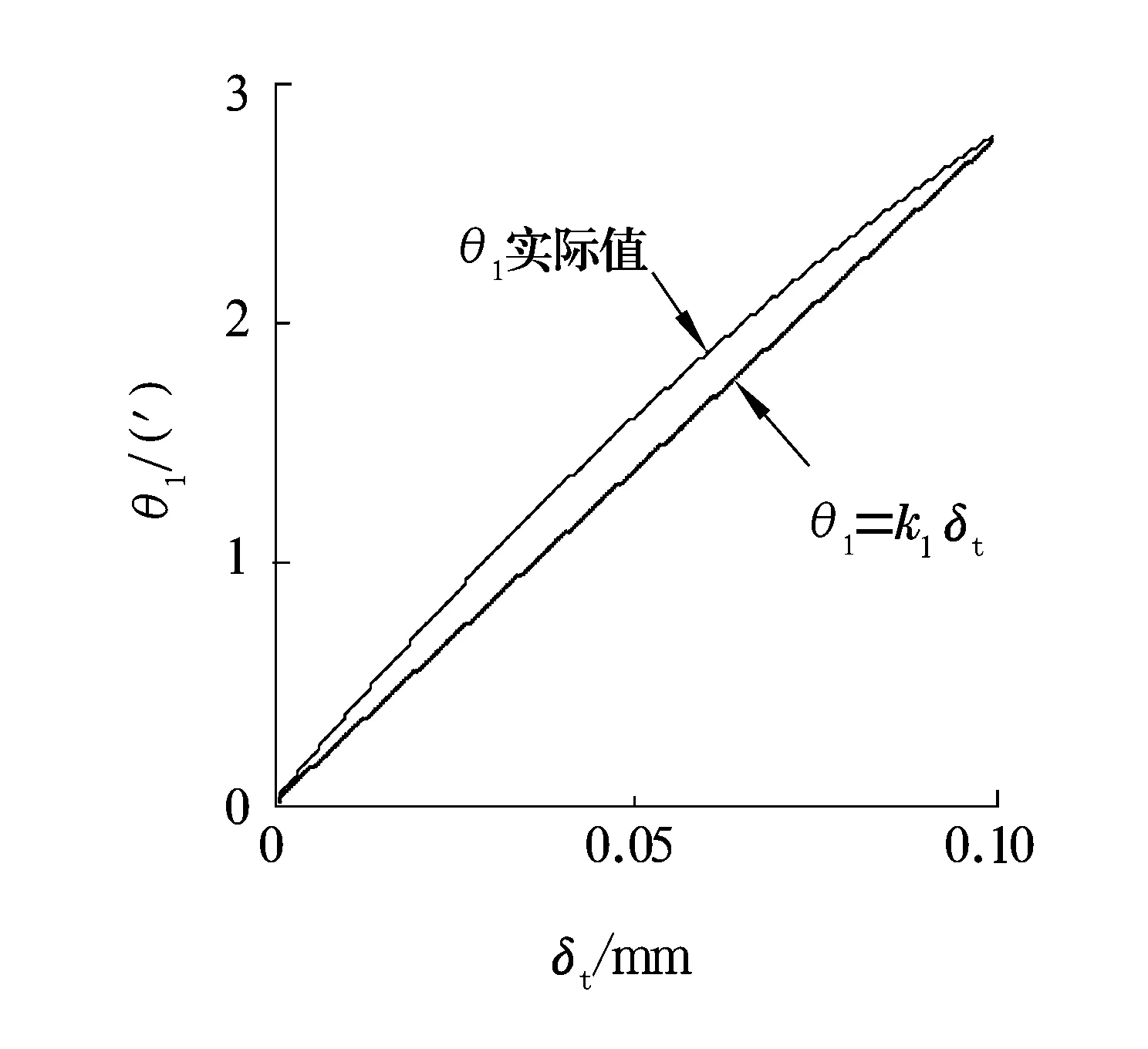
图7 周向间隙角随轴向间隙的变化规律

当α=0～16.84°，β=0～360°时，单个钢球θ1的变化率k1的三维变化规律如图8所示。由图可知，万向节未摆动时，k1为一条直线，随着万向节摆角的逐渐增大，k1由一条直线变为余弦曲线且曲线的波幅越来越大。当α=16.84°，β=0或360°时，k1达到最大值31.42；当α=16.84°，β=180°时，k1达到最小值1.078。万向节转动一周，k1随β角的变化出现一次波动，k1在β=0或360°(以钢球1的起始角度为0)时取得最大值，这是由于钢球的φ角在β=0或360°时取得极小值。将(15)式化为二阶麦克劳林公式为

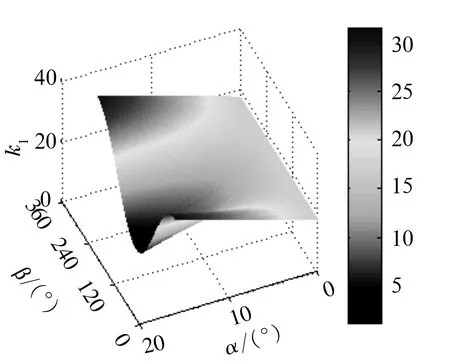
图8 单个钢球k1的三维变化规律

(30)

由(30)式可知，钢球的φ角取得极小值时，一次项系数cosφ取得极大值，这就使得星形套沟道曲率中心与钢球球心的距离l的变化率取得极大值，而k1与l的变化率成正比；k1在β=180°时取得极小值，这是由于钢球的φ角在此时取得极大值，同理可知，此时l的变化率取得极小值。

考虑到6个钢球相互制约，因而，周向间隙角θ1随轴向间隙δt的实际变化率应为6个钢球θ1的变化率k1的最小值。图9为α=0～16.84°，β=0～360°时，实际变化率k1随α和β的变化规律。由图9知，α=0时实际变化率k1为一条直线且最大值为16.88，随着α的增大，实际变化率k1减小，当α接近16.84°，k1趋近于零。万向节转动一周时，实际变化率k1共出现6次波动，其中最大值分别出现在β=30°，90°，150°，210°，270°及330°(以钢球1的起始角度为0)位置，最小值分别出现在β=0，60°，120°，180°，240°及300°位置。由θ1=k1δt可知，随着α的增大实际变化率k1减小，意味着轴向间隙引起的实际周向间隙角θ1随着α的增大而减小，所以增大摆角可有效减小由轴向间隙形成的周向间隙；实际变化率k1的6次波动即是轴向间隙引起的实际周向间隙角θ1的6次波动，而这6次波动正是导致万向节转动时内部各零件窜动与冲击以及使用寿命降低的重要原因。总的周向间隙角θ=θ1+θ2，θ2与θ1有着相同的变化规律，只是大小不同。

图9 实际变化率k1的变化规律

6 结论

(1)当摆角α大于某一值(20°左右)时，轴向间隙与周向间隙角均为零，在摆角、转角不变时，周向间隙角随轴向间隙变化的曲线为一条凸曲线，在轴向间隙的实际范围内，该曲线可近似为一条直线。

(2)单个钢球的周向间隙角θ的变化率k随着摆角α和转角β的变化而变化。当α=0时，k为一定值；当α≠0时，k随着β的变化呈余弦曲线变化；k在β为0和360°时取得极大值，在180°时取得极小值。

(3)实际变化率k随着α的增大总体上有一个由大变小的趋势。万向节转动一周，实际变化率k共出现6次波动，其中波峰分别出现在β=30°，90°，150°，210°，270°及330°位置上，其中波谷分别出现在β=0，60°，120°，180°，240°和300°位置上，而这6次波动是造成万向节转动时内部各零件窜动与冲击以及使用寿命降低的重要原因。