浅谈动能定理对弹簧模型的佯不适用性

王 森 高樱娜 罗琬华

（西南大学物理科学与技术学院，重庆 北碚 400715）

1 动能定理对弹簧模型的佯不适用性现象

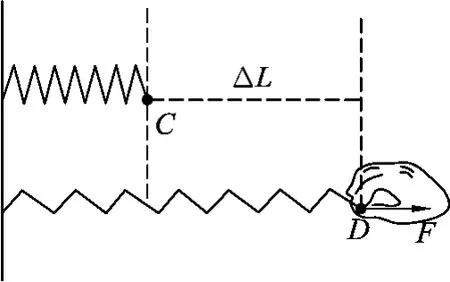
图1

1.1 弹簧的佯不适用性现象

取 人 教 版 （2006）《物理》必修2教材“探究弹性势能的表达式”一节中图7.5－3（本文图1）所示为研究情景：弹簧一端固定在墙上，处于原长，现在另一端施加外力F使弹簧缓慢拉伸.［1］以弹簧为研究对象，设W1表示拉力F对弹簧做的功，W2表示墙壁对弹簧做的功，x表示手与弹簧的接触点的位移，根据文献［2］的结论：求功公式中位移最准确的理解应为受力点即将受力部位看做质点时该质点的位移.有可推知又由于弹簧动能的改变量ΔEk＝0，易知W总≠ΔEk，故弹簧不满足动能定理.

1.2 弹簧系统的佯不适用性现象

弹簧系统，此处界定为含有弹簧的系统，包括不受外力和受外力两种情况.

（1）弹簧系统不受外力.

以图2所示情景分析，在光滑的水平地面上，压缩的弹簧两端分别固定着两个完全相同的物体，放开手后，两物体将在弹簧弹力的作用下做先加速后减速的往复运动.以弹簧和两物体组成的系统为研究对象，因弹簧对物体的力与物体对弹簧的力始终大小相等，方向相反，且弹簧与物体的受力点为同一点，位移相等，故系统内力做功之和为0，考虑到无外力做功，因此系统内、外力做功之和始终为0，这要求系统的动能始终不发生改变.而事实上，系统的动能却在不断变化，这与动能定理相违背，故不受外力的弹簧系统不满足动能定理.

（2）弹簧系统受外力.

图2

以图3所示情景分析，在光滑的水平地面上，弹簧一端固定在墙上，另一端与一物体连接，现压缩弹簧至一定限度后无初速度放开，假设整个过程中无能量损失，弹簧将在水平方向上做先加速后减速的往复运动.以弹簧和物体组成的系统为研究对象，同前文，此处内力做功为0，且弹簧受墙作用力部位始终没有发生位移，因此墙壁对系统做功即外力做功为0，故系统内、外力做功之和始终为0，而系统的动能却在不断地变化着，故受外力的弹簧系统也不满足动能定理.

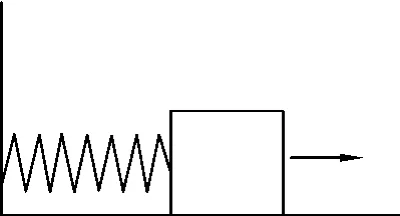
图3

2 动能定理适用范围之理论推导

按研究对象的不同，动能定理分为质点的动能定理与质点系的动能定理；按照质点间距离是否发生改变，质点系又分为不变质点系（即刚体模型）与变化质点系（即形变物体）.一般就动能定理是否适用于质点与不变质点系没有疑问，但对变化质点系（即形变物体）是否适用则意见不一，前文所述弹簧模型对动能定理的佯不适用性现象便是明证.下面重点阐述动能定理对变化质点系的适用性推导.

根据文献［3］，从质点动能定理出发可推导出质点系动能定理［3］，此不赘述.已知质点系动能定理

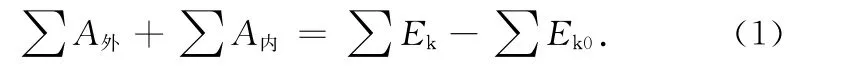
式中∑A外表示质点系外力做功之和，∑A内表示质点系内力做功之和，∑Ek表示质点系的末动能，∑Ek0表示质点系的初动能.其中

式中∑A内非表示质点系内非保守力作功之和，∑A外非表示质点系外非保守力作功之和，∑A外保表示质点系外保守力作功之和，∑A内保表示质点系内保守力作功之和，∑A保表示质点系内外保守力作功之和.

根据势能定义有

式中∑Ep表示质点系末势能，∑Ep0表示质点系初势能.

联立（1）～（3）式得

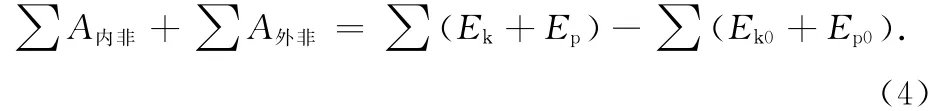
（4）式表明：质点系总机械能的增量等于一切内非保守力和外非保守力所做功的代数和，此即质点系的功能原理.若∑A内非＋∑A外非＝0，即只有保守力做功，则物体的机械能守恒，故机械能守恒定律是质点系功能原理的推论.

上面我们从质点系动能定理到质点系功能原理是以（2）、（3）两式同时成立为前提的，换句话说，质点系功能原理只有在（2）、（3）、质点系动能定理同时成立的条件下才可成立.故易知质点系功能原理的适用范围≤质点系动能定理的适用范围.

3 佯不适用性成因分析

动能定理适用于任何情况，毋庸置疑，但为何会出现动能定理对于弹簧模型的佯不适用性呢？关键在于前文在考虑弹簧时犯下了两个错误：（1）错误地将弹簧看做质点：因弹簧的形变明显，不可忽略其形状大小，故不可看做质点；（2）将弹簧看做质点系时，又定势地认为质点系内力做功之和为0，事实上，弹簧内部质点之间的距离发生了改变即质点间发生了相对位移，根据文献［3］中所证：质点系内力的功等于力与质点间的相对位移的乘积［3］，故知弹簧的内力做功之和必不为0，同样弹簧系统的内力做功之和也不为0.下面我们对图1中所示情景再做分析，以定量计算出此情景下弹簧内力做功之和.

分析.设弹簧外力做功之和为W1，内力做功之和为W2，由动能定理可得

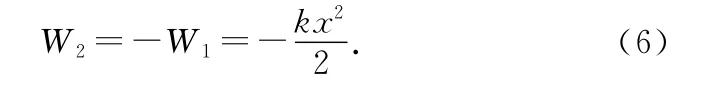
由（6）式知用手缓慢拉伸、压缩一端固定在墙上的弹簧时，弹簧内力做功之和等于外力做功之和的负值，也等于弹性势能的改变量，这也正是教材使用拉力做的功得出弹性势能的表达式的理论依据所在.

4 总结

（1）动能定理适用于任何情况；

（2）功能原理是动能定理在一定条件下的一种变形公式；

（3）弹簧不可看做质点，只能看做质点系，且该质点系内力做功之和必不为0；

（4）用手缓慢拉伸、压缩一端固定在墙上的弹簧时，弹簧内力做功之和等于外力做功之和的负值，也等于弹性势能的改变量，墙壁对弹簧不做功.

1 课程教材研究所.普通高中课程标准实验教科书.物理（必修2）.北京：人民教育出版社，2006.

2 杨凤梅.作用点不固定的力作功的“佯谬”问题.安徽师范大学学报（自然科学版），2001（8）.

3 漆安慎，杜婵英.普通物理学教程 力学（第2版）.北京：高等教育出版社，2005.