寻找接触物系的相关加速度
袁张瑾
(宁波效实中学,浙江 宁波 315010)
有关接触物系接触点的速度特征,在中学物理中常有涉及,也归纳了相应的解决办法.由接触物的力学性质及“接触”的约束条件可知,沿接触面法线方向,接触双方必须具有相同的法向分速度,否则将分离或形变违反接触的约束条件.根据接触物系接触点的相关速度特征,很多教师和学生自然地认为接触点的相关加速度也具有相同的特征,由此出现了一些常见错误.
例题.如图1所示,一个半径为R的半圆柱体沿水平方向以加速度a做匀加速直线运动,半圆柱面上搁着一根只能沿竖直方向运动的竖直杆,当半圆柱体速度为v时,杆与半圆柱体的接触点A与柱心O的连线与竖直方向的夹角为θ,求此时竖直杆的速度和加速度分别为多少?
常见解法:这是接触物系相关速度和相关加速度问题.根据接触物系接触点的速度相关特征,两者沿接触面法向的分速度相同,如图2所示,即

故v杆=vtanθ,方向向上.同理得杆的加速度a杆=atanθ,方向也向上.

图1

图2
由上述方法求出的杆的加速度是否存在问题?杆的加速度值的求解能否简单地从速度值的求解中迁移过去?
以下是笔者对此问题的解法,供参考.
方法1:根据接触物系接触点的加速度相关特征求解.
由图2(a)可知,此时杆相对柱体的速度分量为vt=对应图中大三角形的斜边),方向沿A点切线,如图3所示.若以柱体为参考系,则杆相对柱体有向心加速度为方向指向柱体中心O.杆相对柱体也具有切向加速度,但切向加速度不影响法向加速度,故暂不分析.
现根据接触物系接触点法向加速度分量相等求解,建立矢量式为

图3
a杆对地n=a杆对柱n+a柱对地n,即asinθ,解得若式中a杆>0,则杆的加速度方向向上,反之则向下.
方法2:根据杆的运动只沿竖直方向,杆对地的水平加速度为0的特征求解.
杆相对柱有切向加速度at,设at方向同vt,如图4所示.依据杆对地的水平加速度为0,可列式:ansinθ+atcosθ-a=0,即得因此杆的加速度a杆=atsinθ-ancosθ,代入解得
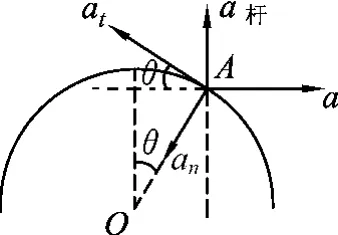
图4
方法3:利用数学方法对位移求两阶导数.
以柱心O为坐标原点,建立如图5所示的坐标系.依题意,柱右移,杆上升,以柱为参考系,杆与柱的接触点从A(x0,y0)升至B(x,y),则有

图5
对y方向上的位移求一阶导数有

再对v杆求导有


导数是高考数学的必考内容,物理竞赛中也有较多的问题用求导可以十分方便地解答.因此在中学物理竞赛辅导中应用导数寻找物体间的相关加速度,这是可行且必要的.

