以Rankine源三维面元法求解三体船纵摇与升沉运动
王 毅 卢晓平 赵军强 段晔鑫
1中国人民解放军镇江船艇学院,江苏镇江212003 2海军工程大学 船舶与动力学院,湖北 武汉430033
以Rankine源三维面元法求解三体船纵摇与升沉运动
王 毅1卢晓平2赵军强1段晔鑫1
1中国人民解放军镇江船艇学院,江苏镇江212003 2海军工程大学 船舶与动力学院,湖北 武汉430033
为对三体船的纵摇与升沉运动进行分析,将三维面元法用于三体船在波浪中的纵摇和升沉计算。依据Rankine源格林函数,基于有航速势流理论建立理论计算模型和数值计算方法,对数学三体船型纵摇、升沉运动响应进行计算,并对计算结果规律进行分析。同时,还对其数值进行模型实验验证。根据计算结果,针对侧体布局对三体船在波浪中纵向运动的影响进行了分析。
三体船;船舶耐波性;三维Rankine源;纵摇;升沉;侧体布局
1 引言
三体船作为一种新型高性能船舶,拥有兴波阻力小、适航性、稳性和总体布置性好等诸多优点,成为目前国内外设计的热点船型之一[1]。近年来,各国建造三体船的步伐也在逐步加快,2000年,英国建造出首艘三体试验船“海神”号后,美国军方派员参与试验并为此船提供了1套综合试验仪器,以对其耐波特性进行精确测试。2008年美国三体濒海战斗舰“独立”号(LCS-2)建成即下水进行实船试验[2]。三体船在其耐波特性上有独特的优势,将成为未来建造舰船的首选船型之一。
本文将三维面元法用于三体船在波浪中的纵摇和升沉计算,依据Rankine源格林函数,按有航速势流建立了理论计算模型和数值计算方法,对不同侧体布局的数学三体船算例进行了理论计算,并将理论计算结果与模型试验结果进行了比较。据此,分析了理论计算结果的准确性,同时,还验证了本文理论方法适用于三体船在波浪中的垂荡与升沉计算。
2 求解船舶在波浪中运动问题的Rankine源方法
按照基于势流理论假设下的时域方法,三维Rankine源法能够有效处理航速问题。由于Rankine源只满足基本拉氏方程,不满足任何边界条件,因而具有较强的灵活性,在定常非线性兴波数值模拟上取得了成功[3]。此外,该方法在处理物体时域运动上也获得了深入研究与应用[4]。本文采用基于Rankine源的时域方法,使用简单源格林函数,在三体船表面、自由表面上同时布置源汇进行计算。同时,采用基于速度势分解的方法,将自由表面条件在水面展开,保留以波高为基数的有限阶数项,可在水面上满足相应的自由表面条件。由叠加原理将流场中非定常速度势分解为入射势、绕射势和辐射势。其中,入射势是给定无物体存在的入射波流场;辐射势是物体运动产生的流体扰动场。绕射势和辐射势可以通过拉普拉斯方程、线性化自由表面边界条件、物面边界条件以及远场辐射条件进行求解。
2.1 速度势及其数学模型
考虑到在波浪中以匀速U前进的船舶,定义了3个坐标系统,分别是空间固定坐标系、随船坐标系和参考坐标系。其中,随船坐标系在耐波性计算中使用得最多。以下三维Rankine源方法的数学模型均基于此标架进行描述。假设流体无黏、无旋、不可压缩,流场存在速度势Φ。在线性范围内,可以将速度势分解为入射波速度势Φ1和扰动速度势Φ2之和。

扰动速度势Φ2可满足Laplace方程,
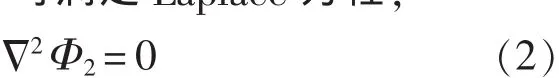
扰动速度势Φ2速度势满足边界条件如下:
线性化的自由面运动学边界条件,


当z=0时,ζ为波高,物面边界条件可满足不可穿透条件,

当z=0时,线性化动力学的自由面边界条件,
式中,Vn为物体表面法向速度,对固定面VnA=0。由于Rankine源不满足任何边界条件,因此需要一个远场辐射边界条件,现有方法有数值阻尼消波区[4]、混合源法[5]以及多次透射法[6],本文采用较为简单实用的数值阻尼消波区,可满足辐射(远场)条件。
2.2 运动方程
船体在波浪中的运动是以刚体在无限流体区域中的运动作为基础,采用随体坐标系,船体表面压力由线性Bernoulli表示:
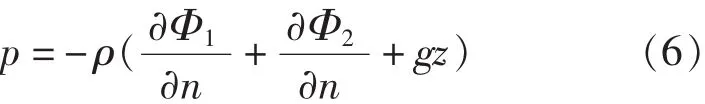
船体的受力由船体表面压力表示:

其中,(n1,n2,n3) =n,(n4,n5,n6) =r×n。 求得船体扰动速度势后,由压力积分可得到相应船体受力。
将三体船体视作刚体,其运动方程为:
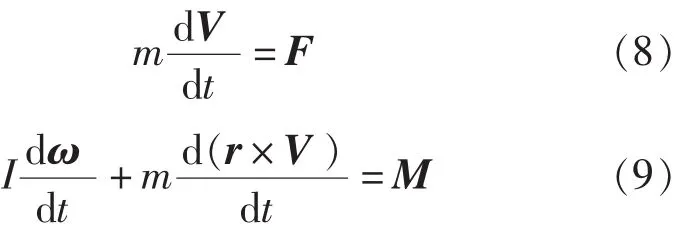
式中,m为质量矩阵,可表示为:
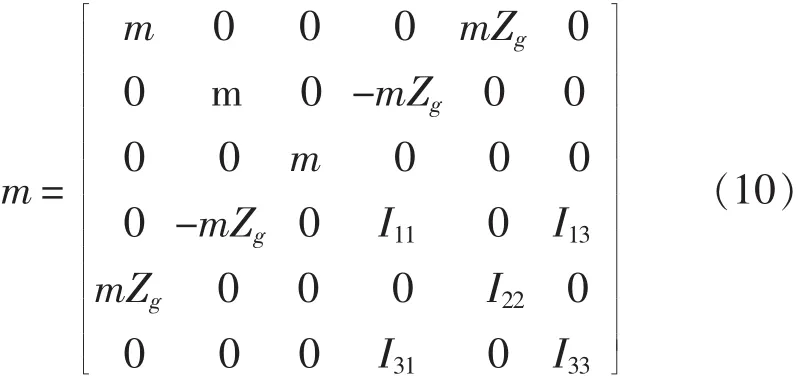
F可由式(7)得到,I为三体船的船体惯性矩矩阵。
2.3 积分方程
由格林第三公式[6],应用Rankine源简单格林公式,可得积分方程如下:
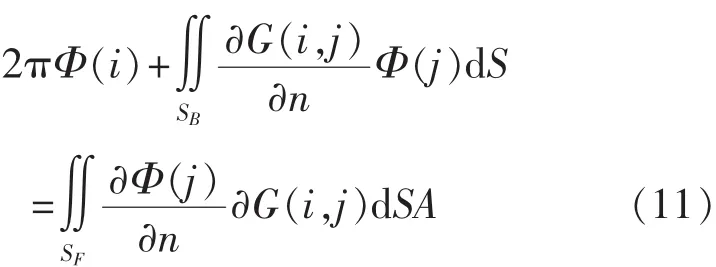

2.4 辐射边界条件处理
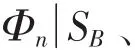
计算中,在运动学自由水面条件加入阻尼项,
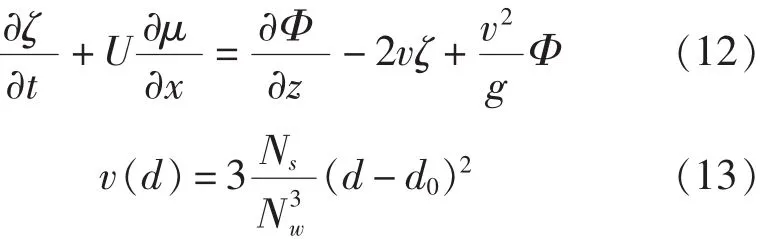
式中,d为计算点距计算域中心距离;d0为阻尼区开始位置距计算域中心距离;Ns和Nw为阻尼控制系数,可控制阻尼大小。为了提高阻尼区效率,必须选择适当的阻尼区长度和系数,以使波浪能够完全吸收。因此,阻尼系数应从零开始递次增加。
从以上介绍的三维Rankine源方法可以看出,其优点是模型中的格林函数适用性灵活,既适用于小摇幅假设下的线性化边界条件,也适用于大摇幅下的非线性边界条件[7]。因此,将该方法应用于三体船的耐波计算具有较强的优势。其直接计入了三体船片体间的水动力干扰作用,理论上还可用于三体船的耐波性理论计算预报。
3 算例与计算结果分析
本文根据上述数学模型,利用FORTAN工具进行编程计算。对于非线性计算采用时间历程方式来表示;而对于线性计算则将结果转换为频域的方式来表示。通过辐射问题、绕射问题求解而得到垂荡和纵摇的附加质量和阻尼、一阶绕射力,并将主扰动力带入线性运动方程求解,从而得到三体船纵摇和升沉响应。
3.1 基本参数
三体船算例的中间主船体(中体)远大于两对称侧体,中体和侧体均为几何相似的Wiglley数学船型[8]。三体船算例侧体布局参数由侧体与中体横向间距p,纵向间距a做出规定,a、p的意义与坐标系位置如图1所示。
对照试验船模取1∶20缩尺比的三体船模进行计算,其主要参数如表1所示。
对照船模试验数据,分别取 a=0.5,p =0.6;a=0.5,p =0.75;a=1.5,p =0.75 下 3 种布局参数对船模在表2所示的速度、波长和遭遇频率进行垂荡与升沉计算。
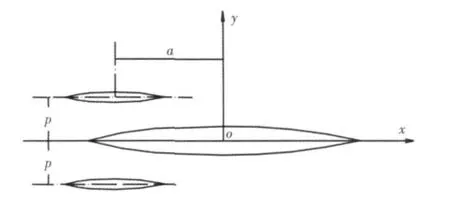
图1 三体船算例坐标系与参数示意Fig.1 Coordinate system and ouriggers configuration parameters of trimaran
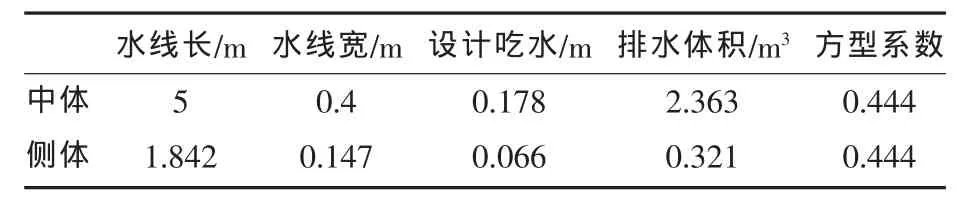
表1 三体船模算例主尺度和船型参数Tab.1 Principal characteristics of the trimaran scaled model
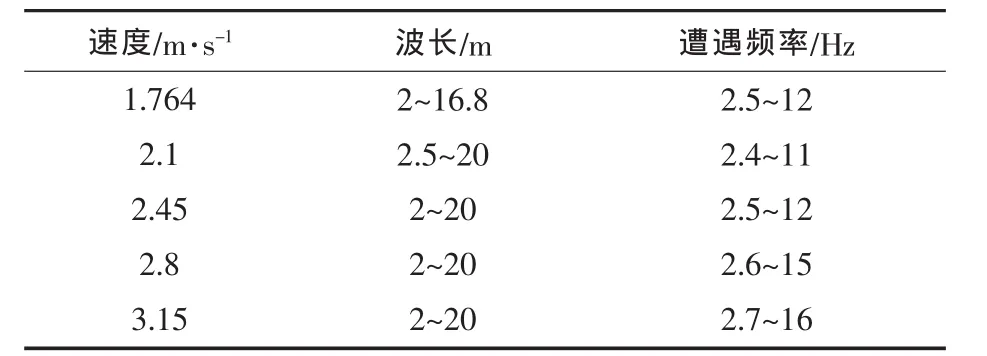
表2 三体船模算例计算参数Tab.2 Model calculation parameters of the trimaran
3.2 面元划分
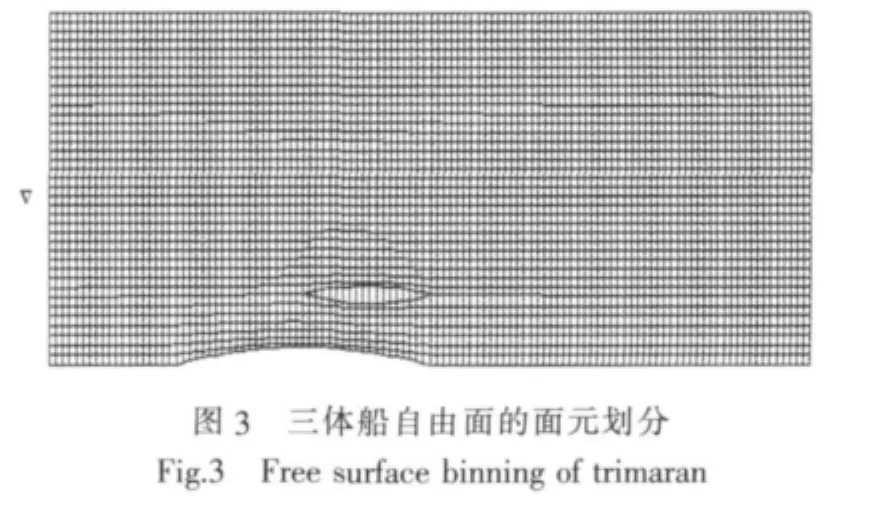
Rankine源方法需对自由面面元与船体面元进行定义,本文采用5倍船长为半径的自由面面元作为自由面截断的范围,Wigley三体船使用H型贴体坐标网格,其体面元划分如图2所示,图3给出了Wigley三体船的自由面网格图。

图2 三体船体的面元划分Fig.2 Hull binning of trimaran
3.3 纵向运动幅值频率响应计算
根据对频率响应的求解方法[6],首先计算三体船不同速度下的垂荡幅值响应函数η3。侧体布局为 a=0.5 m,p =0.6 m 时三体船在不同航速迎浪状态下垂荡频率响应结果如图4所示。其中Fn为傅汝德数。
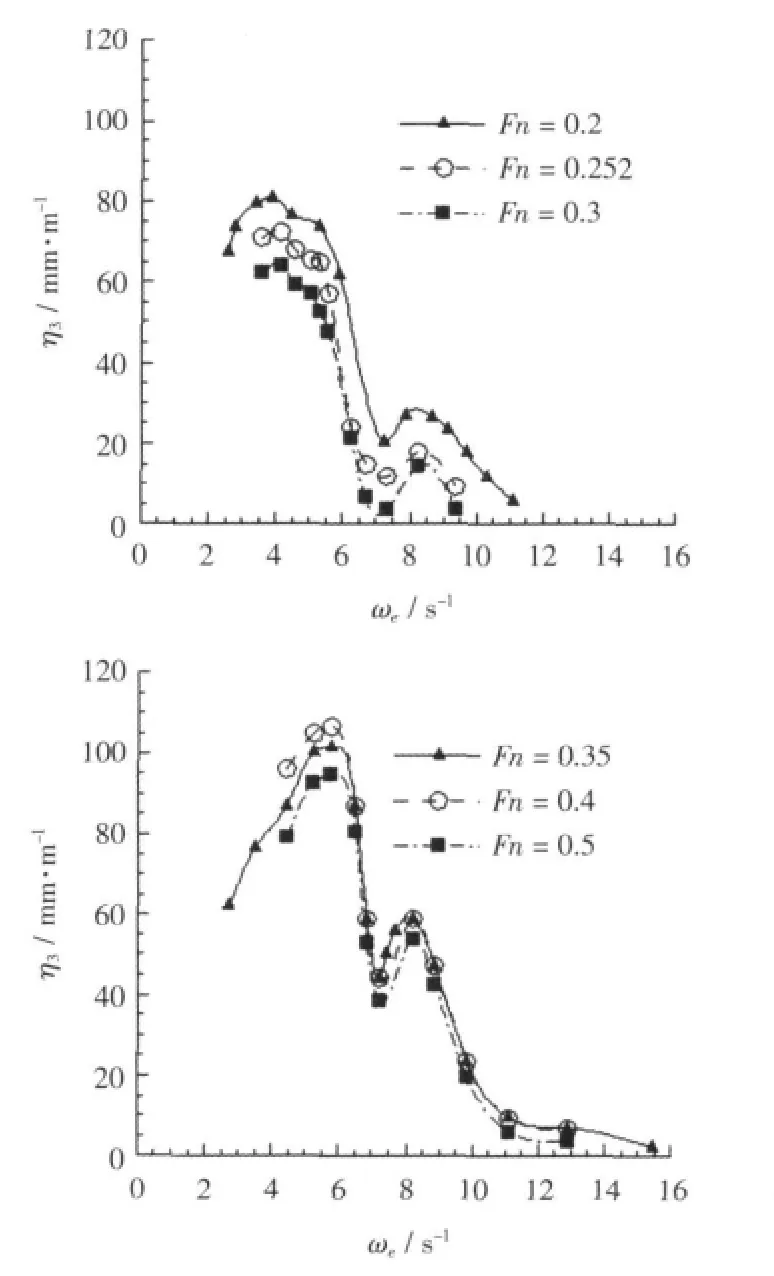
图4 不同航速下垂荡响应曲线Fig.4 Heaving response curve at different speed
由图4可见,随着航速的增加,垂荡幅度变大,其峰值频率也随航速变化。在通常的速度下,均出现第二峰值,第二峰值是三体船等多体船的特征,由片体间干扰所致[9]。
分别取速度为 1.764 m/s和 3.15 m/s的不同侧体布局方案来对应傅汝德数划分低速船与高速船状态区间,得到的三体船垂荡频率响应结果如图5所示。
由图 5 可见,在速度为 1.764 m/s时,随着侧体横向间距的增大,垂荡幅值明显减小,随着侧体位置纵向位置(距中心)靠后,垂荡在频率中段有所减小,其余频段有所增加;在速度3.15 m/s时,随着侧体横向间距的增大,垂荡在低频时有所增加,随后趋于一致,随着侧体位置纵向位置(距中心)靠后,垂荡明显减小,在高频时趋于一致。另外,对于垂荡响应而言,在高速状态侧体纵向位置的影响要大于横向间距的影响,而在低速状态时则相反。但在不同速度下,侧体纵向位置(距中心)靠后均对三体船耐波运动起到有利影响,从而减小了垂荡幅值。
与垂荡响应类似,在侧体布局为a=0.5 m,p=0.6 m的不同速度下,三体船迎浪状态纵摇频率响应η5结果如图6所示。
由图6可见,随着航速的增加,纵摇幅度变大,纵摇峰值频率从低频向高频移动。
与垂荡一致,分别取速度为 1.764 m/s和3.15 m/s,3个不同布局方案得到的迎浪状态纵摇频率响应结果如图7所示。
由图7可见,随着侧体位置离主体横向间距增大,速度为1.764 m/s时纵摇幅值在低频时纵摇频率有所增加,在其余频段明显减小;而在速度为3.15 m/s时,纵摇幅值明显减小,在高频时趋于一致。随着侧体纵向位置(距中心)靠后,在速度为1.764 m/s时,在低频段纵摇幅值明显减小,在其余频段趋于一致;在速度为3.15 m/s时,在低频时,纵摇幅值有所增大,其他频段基本一致。从以上分析可以看出,横向间距与纵向位置的改变都对纵摇有较大影响,在低速与高速时横向间距增大都对三体船纵摇起到较大的有利影响,纵向位置(距中心)靠后对三体船纵摇都起到了不利影响,但影响较小。
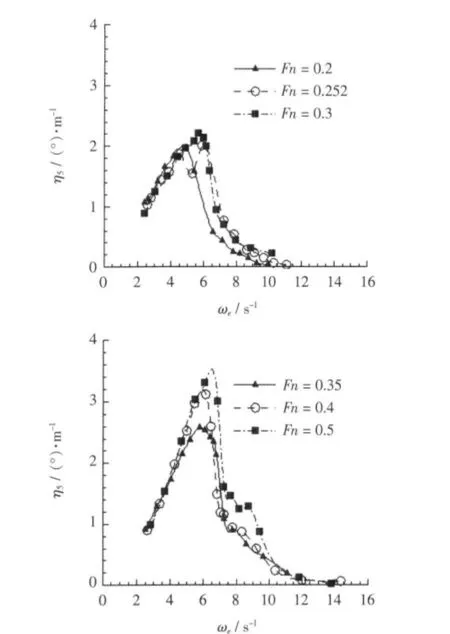
图6 不同航速下纵摇响应曲线Fig.6 Pitching response curve at different speed
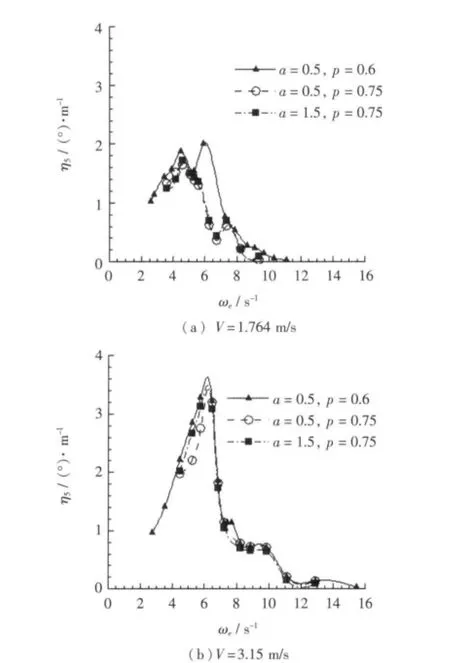
图7 不同侧体布局的纵摇响应曲线Fig.7 Pitching response curve in different side hull positions
现将计算结果(RAK)与模型试验结果(EXP)进行对比,其中模型试验方案参数与计算模型参数一致,与文献[10]为同一批次试验,均为Wiglley片体,三体船模型如图8所示。

图8 三体船试验模型Fig.8 Test model of trimaran
侧体布局为 a=0.5 m,p=0.6 m 时,各速度下得到垂荡频率响应曲线如图9所示。
侧体布局为 a=0.5 m,p=0.75 m 时, 不同横向侧体布局各速度下模型试验垂荡响应曲线与计算垂荡响应曲线对比如图10所示。
侧体布局为 a=1.5 m,p=0.75 m 时,不同纵向侧体布局各速度下模型试验垂荡响应曲线与计算垂荡响应曲线对比如图11所示。
将纵摇响应计算结果与模型试验结果进行对比,侧体布局为 a=0.5 m,p =0.6 m 时,各速度下纵摇频率响应曲线如图12所示。
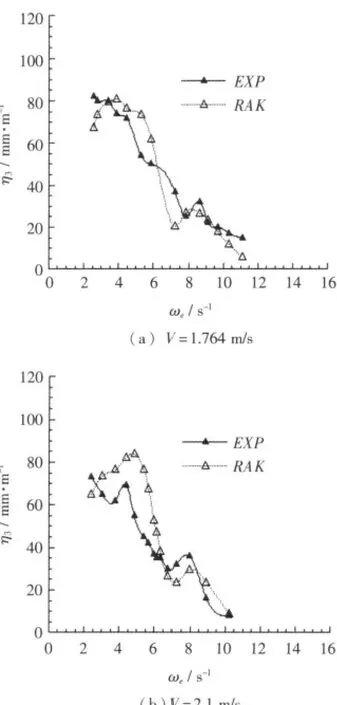
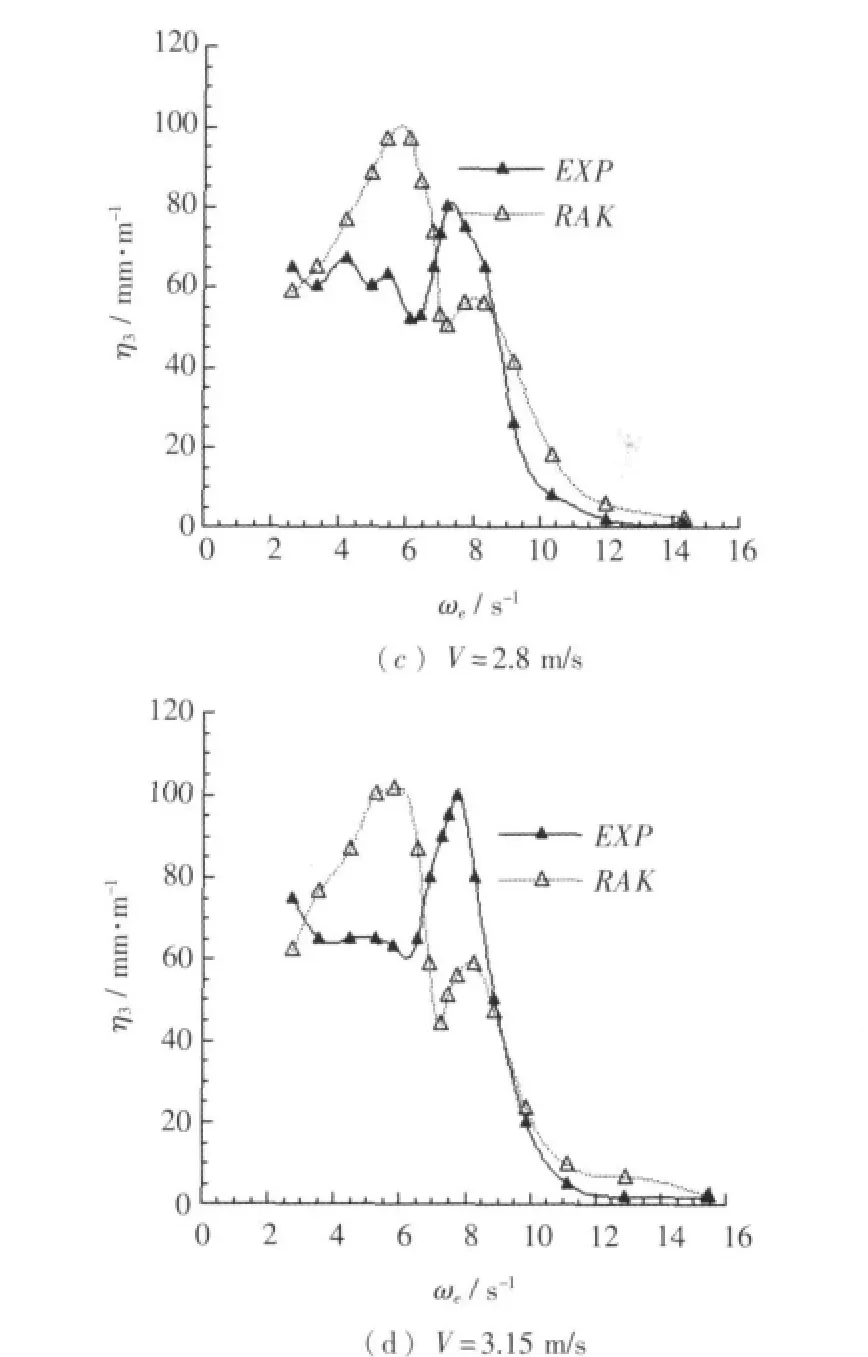
图9 不同航速下垂荡频率响应计算曲线与试验曲线对比Fig.9 Comparison calculation curve with test curve of heaving response at different speed
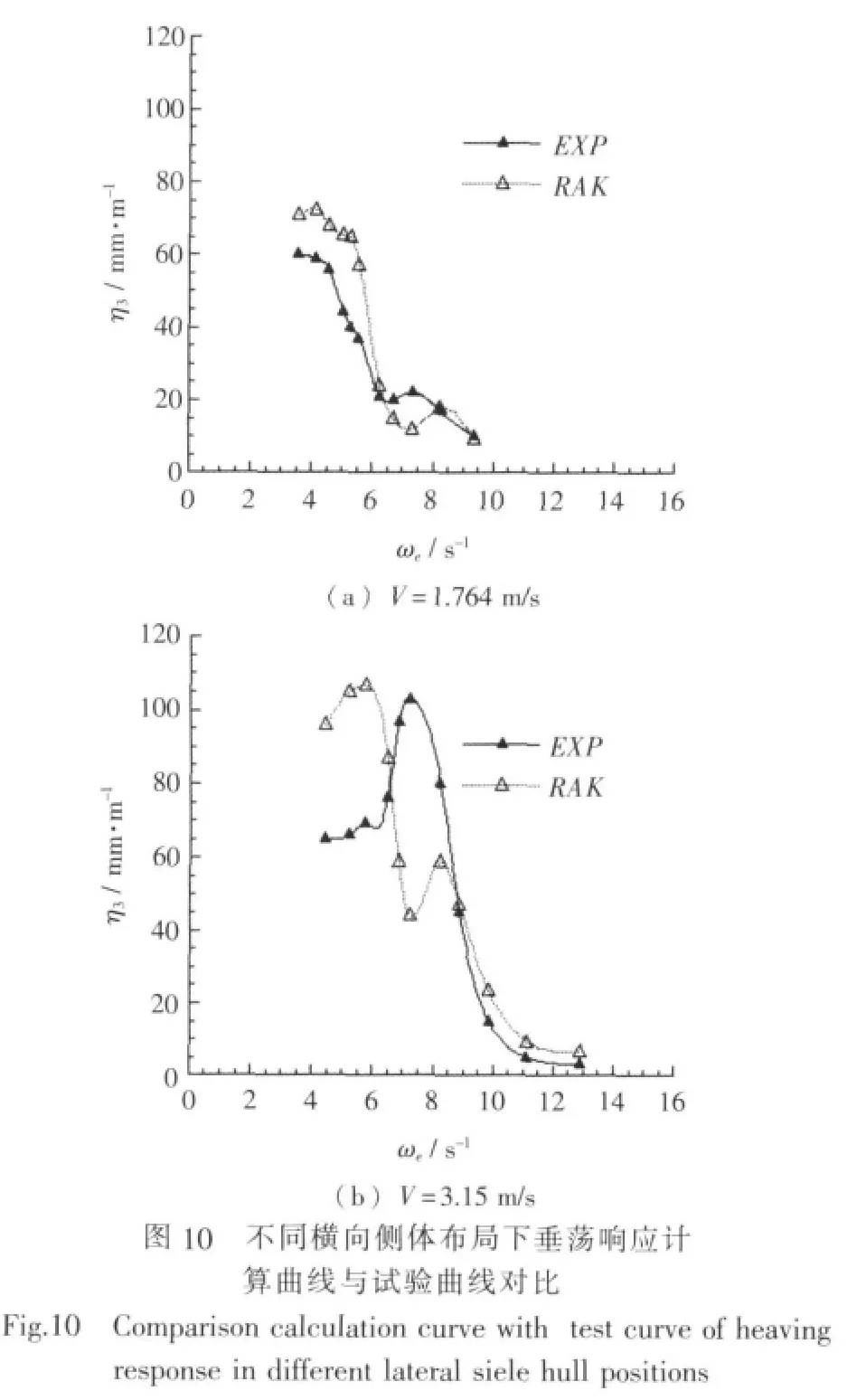
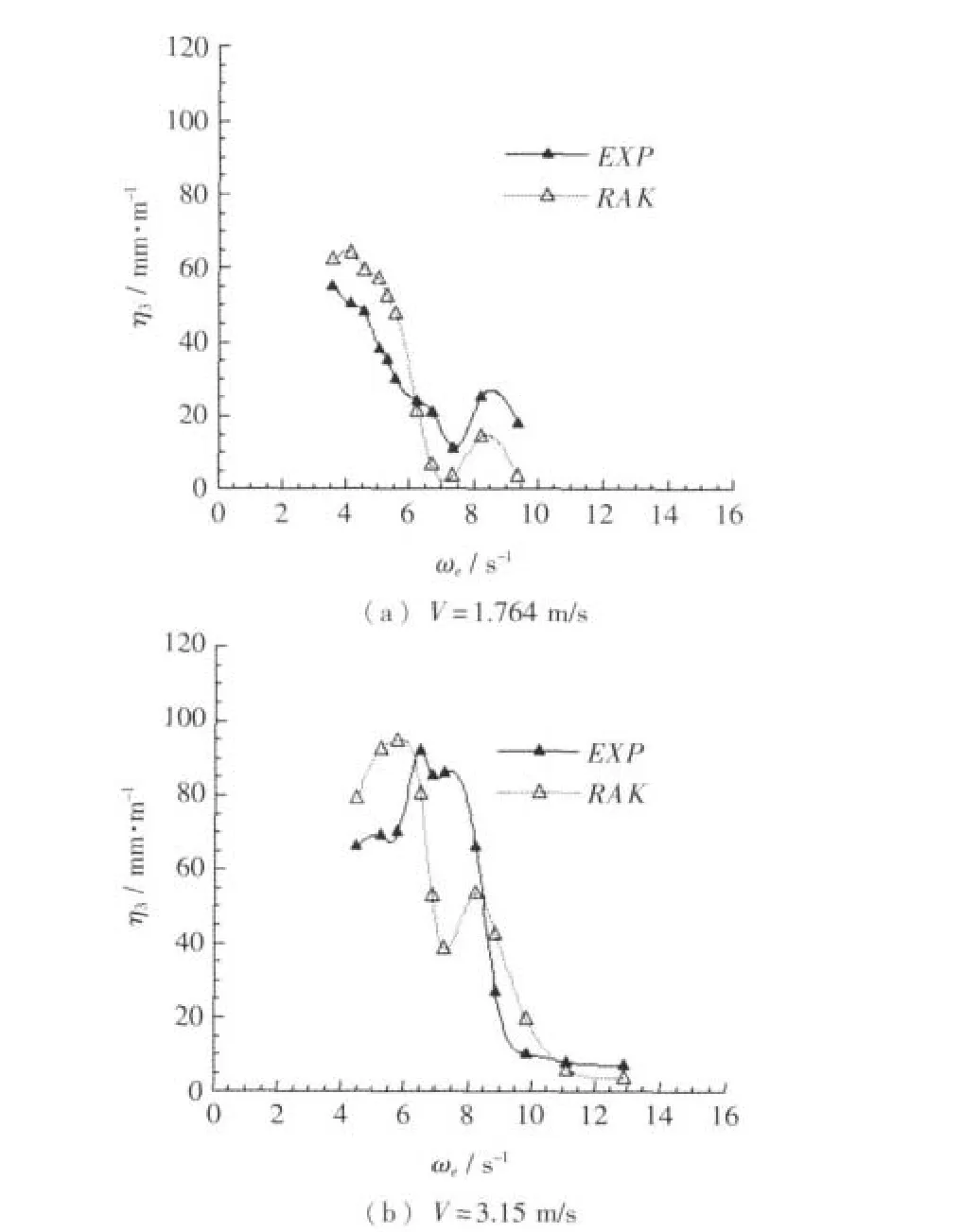
图11 不同纵向侧体布局下垂荡响应计算曲线与试验曲线对比Fig.11 Comparison calculation curve with test curve of heaving response in different vertical side hull positions
侧体布局为布局 a=0.5 m,p =0.75 m 时,不同横向侧体布局各速度下模型试验纵摇响应曲线与计算纵摇响应曲线对比如图13所示。
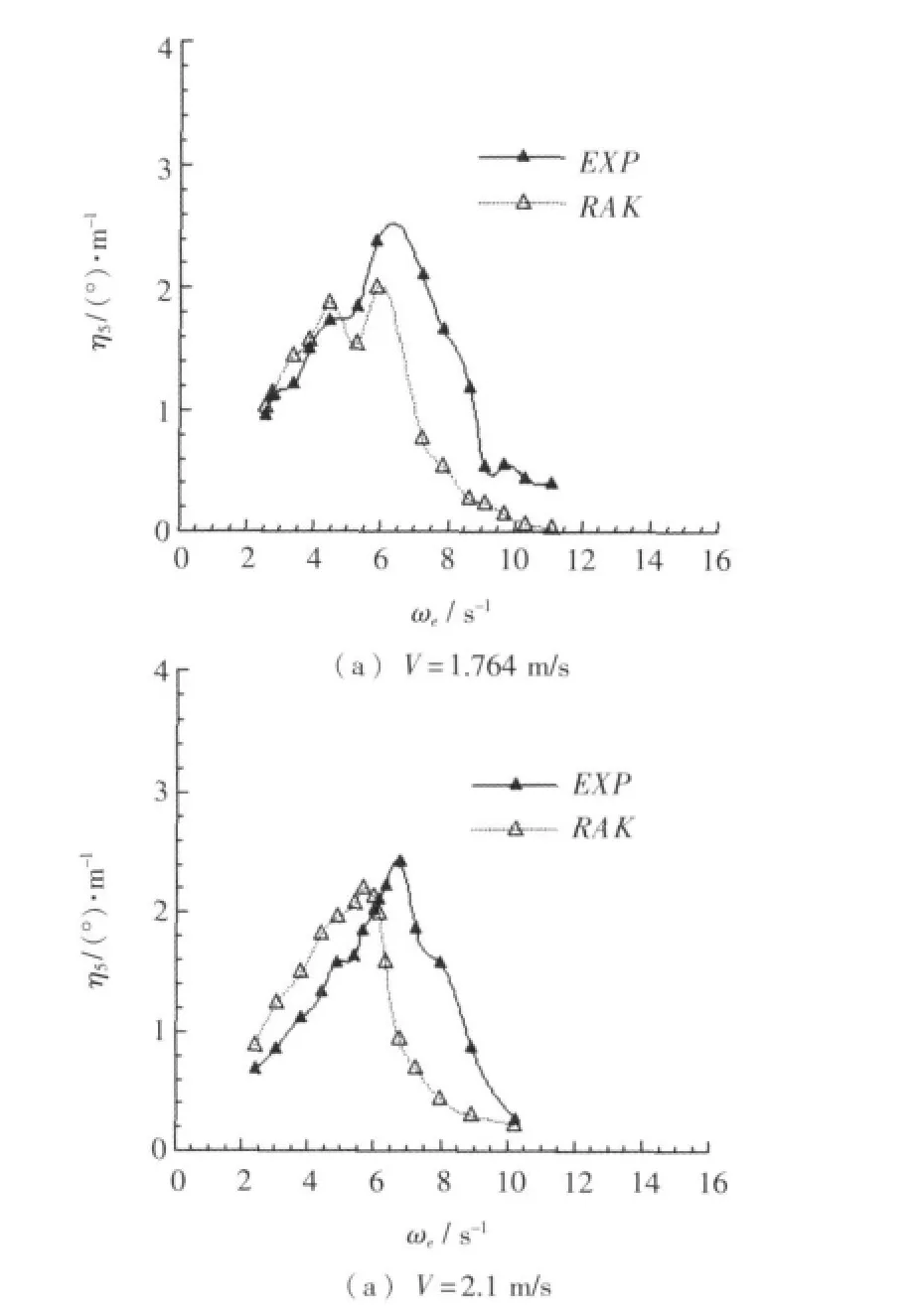
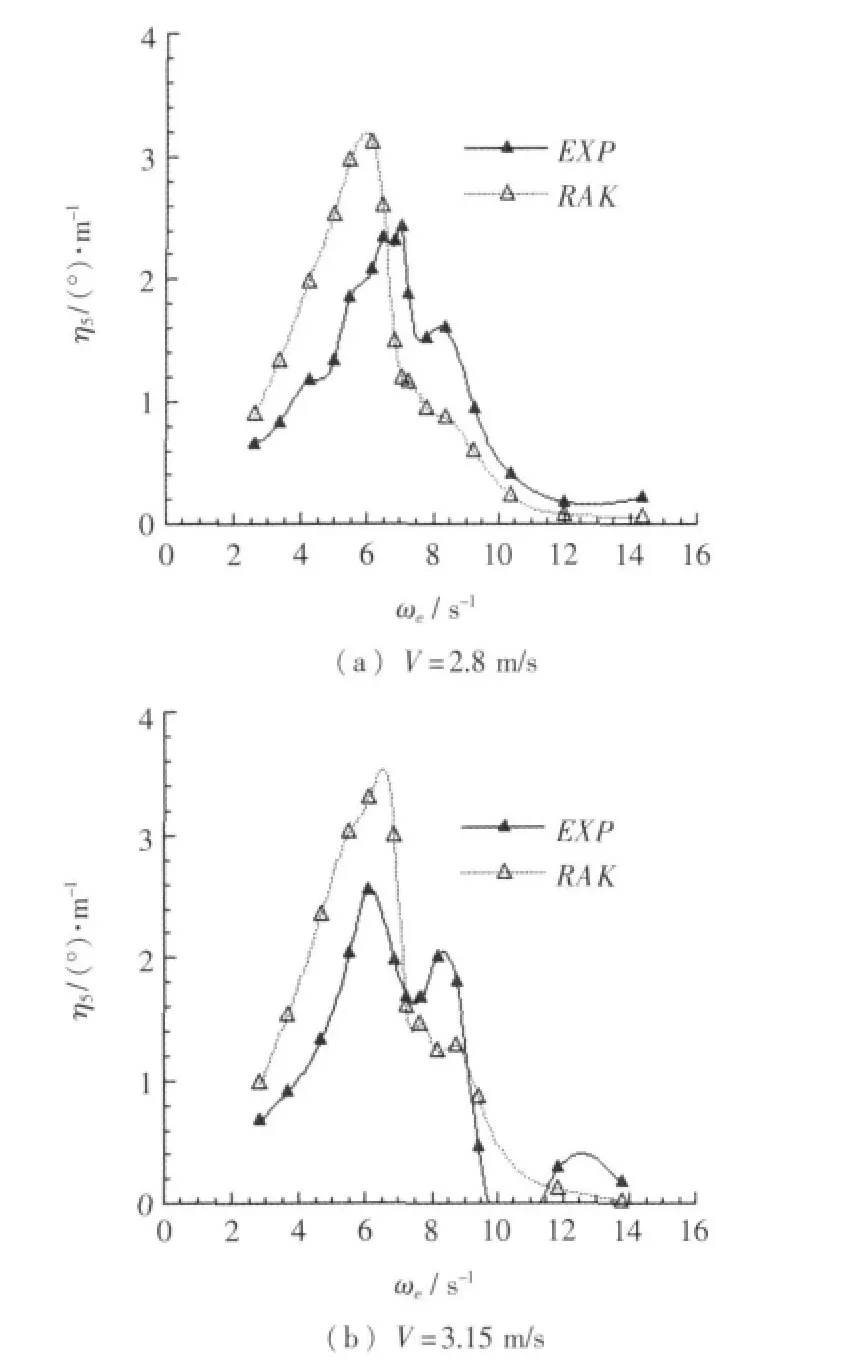
图12 不同航速下纵摇频率响应计算曲线与试验曲线对比Fig.12 Comparison calculation curve with test curve of pitching response at different speed
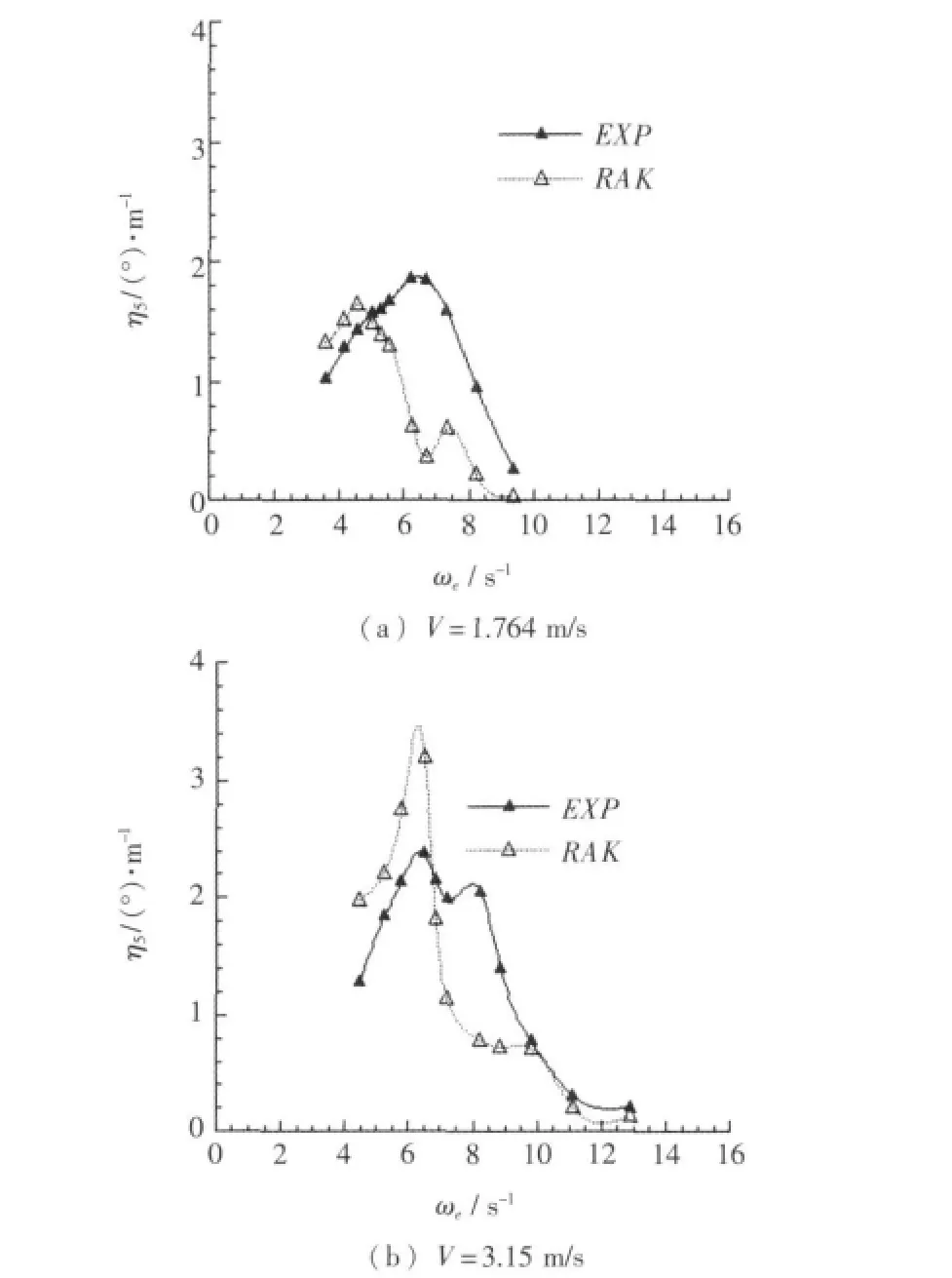
图13 不同横向侧体布局下纵摇频率响应计算曲线与试验曲线对比Fig.13 Comparison calculation curve with test curve of pitching response in different lateral side hull positions
侧体布局为布局 a=1.5 m,p =0.75 m 时,不同纵向侧体布局各速度下模型试验纵摇响应曲线与计算纵摇响应曲线对比如图14所示。
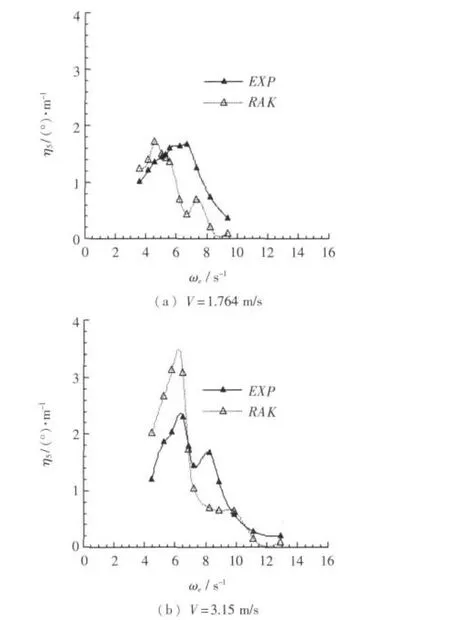
图14 不同纵向侧体布局下纵摇频率响应计算曲线与试验曲线对比Fig.14 Comparison calculation curve with test curve of pitching response in different vertical side hull positions
在各种侧体布局方案、各种速度下,三维Rankine源法得到计算结果与模型试验结果曲线相比,二者在垂荡响应幅值数量级相同。在低速时计算曲线与试验曲线吻合较好;在中高速时,计算所得曲线变化趋势也与试验曲线总体一致。另外,在改变侧体位置时,将计算结果与模型试验结果进行比较,其吻合程度总体上变化不大。尤其从图10、图13中可见,与模型试验曲线比较,计算曲线较为准确地反映了侧体横向间距变化引起的垂荡和纵摇响应曲线的变化,而且也准确地反映了航速对垂荡响应曲线的影响。由图11、14可见,在改变侧体纵向位置时,计算曲线与模型试验曲线峰值频率基本一致,计算曲线同样较为准确地反映了侧体纵向位置变化引起的垂荡和纵摇响应曲线的变化。但同时,从图9、图12、图14等可以看到在某些速度试验与计算结果在峰值对应频率,峰值大小上仍有差异,经分析计算模型主要在于网格域大小、疏密控制参数设定上不是能够对所有速度状态都能良好表现,模型试验在于试验环境条件本身还有局限性,不能全面反映三体船型特性,导致三体船纵摇和垂荡响应不能完全一致。同时,计算采用Rankine面元法基于势流理论,忽略了流体分离影响。在本文纵摇升沉幅值与计算三体船尺度相比为小量时,流体分离产生粘性阻尼较小,计算所得结果能够较好地反映兴波引起阻尼的影响,与考虑粘性阻尼的模型试验相比,结果误差精度范围基本满足纵摇和升沉运动预报需要。综上所述,采用三维Rankine方法在三体船在波浪中的垂向运动计算是有效的。三维Rankine源法较好地反映了侧体布局对三体船在波浪中纵向运动响应的影响。
4 结论
利用三维Rankine源方法对三体船耐波性进行了计算,通过计算得到了三体船升沉与纵摇运动幅值频率响应,并将计算结果与模型试验结果进行了比较两者总体趋势一致;三维Rankine源法和其他三维面元法在三体船在波浪中纵向运动计算结果精度大致相当;三维Rankine源法较好地反映了三体船侧体布局对运动响应的影响。与线性理论导出的方法相比,三维Rankine源方法计算时间较三维移动脉动源方法更短,计算方法更灵活,有望发展为非线性计算方法。但三维Rankine源法在自由面划分网格,布置源汇等方面人为因素较多,需要较多的计算经验,三维移动脉动源法则人为因素较少,结果较为稳定。
三体船耐波性需开展进一步研究,如三体船在不规则波上的运动、三体船的横摇运动特性、三体船耐波性非线性理论预报方法建立,三体船耐波性标准及船型优化等都是迫切需要深入研究的课题。
[1]卢晓平,郦云,董祖舜.高速三体船研究综述[J].海军工程大学学报,2005,17(4):43-52.
LU X P,LI Y,DONG Z H.A research summary on high speed trimaran[J].Journal of Naval University of Engineering,2005,17(4):43-52,
[2]卢晓平,王中,孙永华,等.Rankine源Dawson型方法求解三体船兴波阻力[J].华中科技大学学报(自然科学版),2008,36(11):103-107.
LU X P,WANG Z,SUN Y H,et al.Solution to wave resistance to trimanan using Rankine sources method of Dawson type [J].Huazhong University of Science of Journal and Technolgy (Natural Science),2008,36(11):103-107.
[3]RAVEN H C.Inviscid calculations of ship wave making capabilities, limitations, and prospects[C]//22nd Symposium on Naval Hydrodynamics,1998:69-76.
[4]HUANG Y F,SCLAVOUNOS P D.Nonlinear ship motions[J].Journal of Ship Research,1998,42(2):120-130.
[5]陈京普,朱德祥,刘晓东.水面船非线性兴波数值方法研究[J].水动力学研究与进展,2008,23(4):357-363.
CHEN J P,ZHU D X,LIU X D.Study of numerical method for nonlinear ship wave making[J].Chinese Journal of Hydrodynamics,2008,23(4):357-363.
[6]戴遗山.舰船在波浪中运动的频域与时域势流理论[M].北京:国防工业出版社,1998.
[7]XU G,DUAN W Y.Time domain simulation of irregular wave diffraction[C]//8th International Conference on Hydrodynamics,2008:115-131.
[8]CONOLLY J E, ENG B S C.Rolling and its stabilisation by active fins [J].RINA,1968,111(1):1-8.
[9]王毅,卢晓平.三体船在波浪中的垂荡与升沉计算及其结果分析[C]//第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会文集.成都:中国力学学会,中国造船工程学会,2009: 634-644.
WANG Y,LU X P.A Calculation and Its Result Analysis to Trimaran Heave and Pitch on Waves[C]//Proceedings of the 9th National Congress on Hydrodynamics and 22nd National Conference on Hydrodynamics.Chengdu,2009:634-644.
[10]卢晓平.高速三体船在波浪中纵向运动研究[C]//第九届中国国际船艇展暨高性能船技术报告会论文集.上海, 2004:48-54.
LU X P.Research on longitudinal motion performance of trimaran[C]//The Ninth China International Boat Show and high performance ship technical reports collection.Shanghai, 2004:48-54.
Three Dimensional Panel Method Based on Rankine Source for Calculating Pitch and Heaving of Trimaran
Wang Yi1Lu Xiao-ping2Zhao Jun-qiang1Duan Ye-xin1
1 Zhenjiang Watercraft College of PLA,Zhenjiang 212003,China 2 College of Naval Architecture and Power, Naval University of Engineering, Wuhan 430033, China
In order to analyze the pitch and heaving motion for trimaran on waves, the three dimensional panel method (3DP) was used.Based on Green Function of the three dimensional Rankine source, the theoretical model and numerical calculation procedure for wave motion potential flow theory with ship speed were developed, and calculating the motion response of pitch and heaving of Wigley trimaran.And the law of the calculation results was analyzed and compared with the model test results.Furthermore,the influence of side hull position on the longitudinal motion of trimarans on waves was analyzed.
trimaran; ship seakeeping; three dimensional Rankine source; pitch; heaving; side hull position
U661.32
A
1673-3185(2012)02-29-08
10.3969/j.issn.1673-3185.2012.02.006
2011-06-27
海洋工程国家重点实验室项目(0812)
王 毅(1985- ),男,硕士,助教。 研究方向:船舶流体力学。E-mail:yiyiff2003@yahoo.com.cn
卢晓平(1957-),男,教授,博士生导师。研究方向:船舶流体力学。E-mail:luxiaoping100@163.com
王 毅。
[责任编辑:饶亦楠]

