环++…+上的一类常循环码
李 岩, 朱士信
(合肥工业大学 数学学院,安徽 合肥 230009)
环++…+上的一类常循环码
李 岩, 朱士信
(合肥工业大学 数学学院,安徽 合肥 230009)
文章研究了环R=++…+上任意长的(1+uβ)-常循环码的结构,确定了环R上长为N=的不同的(1+uβ)-常循环码的个数和这样的码所含码字的个数,并得到环R上的(1+uβ)-常循环对偶码的结构。
常循环码;Galois环;对偶码;离散傅里叶变换;零化子
0 引 言
有限域上的编码理论已经比较成熟,在文献[1]中得到某些二元非线性码可以看作是Z4环上的Gray像,使得近年来环上码的研究成为编码理论学家研究的一个热点。特别地,有限环上常循环码的研究也成为研究热点之一。文献[2]研究了Z4上奇长负循环码;文献[3]运用变换的方法将Z4上所有偶长的负循环码分类;文献[4]研究了环Z4上的循环码的生成元;文献[5]研究了有限链环上循环码和负循环码的结构;文献[6]研究了GR(2a,m)上长为2s的负循环码的结构,并确定了这些负循环码的汉明距离;文献[7]研究了F2+uF2+u2F2上线性码及其Gray像;近年来重根循环码得到广泛的研究,文献[8-9]研究了Fp[u]/〈um〉及上一类任意长的常循环码,文献[10]研究了Z2a上偶长的对偶和自对偶负循环码。
本文研究了环R=Fpm+uFpm+…+uk-1
上任意长的(1+uβ)-常循环码,得到R的Galois扩环上的长为ps的(1+uβ)-常循环码的结构,并用这些码来构造R上长为N=psn的(1+uβ)-常循环码,其中(n,p)=1;确定了R上给定长的不同的(1+uβ)-常循环码的个数和这样的码所含码字的个数;得到了环R上的(1+uβ)-常循环对偶码的结构。
1 基本概念
设R=Fpm+uFpm+…+uk-1,其中uk=0。R是局部环,其极大理想为〈u〉,剩余域为。设q=pm,N=psn,其中(n,p)=1。环R上长为N的码C是RN的一个R-子模,定义循环置换σ:RN→RN为:(c0,c1,…,cN-1)→ (cN-1,c0,…,cN-2)。对环R中任一可逆元λ,定义λ-常循环置 换σλ:RN→RN为:(c0,c1,…,cN-1)→(λcN-1,c0,…,cN-2)。如果C为R上的码,满足σ(C)=C,则称码C为循环码。如果σλ(C)=C,则称码C为λ-常循环码。对于任意c=(c0,c1,…,cN-1)∈C,设c(x)=c0+c1x+…+cN-1x(N-1)为其在环R[x]/〈xN-λ〉中的多项式表示,则C是环R上的λ-常循环码等价于C(x)是环R[x]/〈xN-λ〉的理想。
设为f(x)∈R[x]模u化简后的多项式。若在[x]中不可约,则称f(x)在R[x]中基本不可约。设R的 Galois扩环为GR(R,r)=R[x]/〈h(x)〉,其中h(x)是R[x]中次数为r的首一基本不可约多项式。则GR(R,r)是局部环,其极大理想为〈u〉,剩余域为。设I是模n的q-分圆陪集的代表组成的集合,r是q模n的阶,ξ是中的n次本原单位根。由Hensel引理知GR(R,r)也包含一个n次本原单位根ξ。设u=(u0,u1,…,uN-1),v=(v0,v1,…,vN-1)∈RN。定义u和v的内积为:
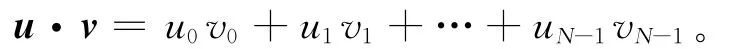
如果u·v=0,则称u和v正交。设C是R上长为N的线性码,定义C⊥={u|u·v=0,∀v∈C}。如果C⊆C⊥,则称C是自正交的。如果C=C⊥,则称C是自对偶码。
定义1 设I是R[x]/〈xN-λ〉的理想,定义A(I)={g(x)|g(x)f(x)=0,∀f(x)∈I}为I的零化子,则A(I)也是R[x]/〈xN-λ〉的理想。
定义2 设f(x)=a0+a1x+…+arxr∈R[x]/〈xN-λ〉,则f*(x)=xrf(x-1)=ar+ar-1x+…+a0xr称为f(x)的互反多项式。
2 主要结果
2.1 (1+uβ)-常循环码
下面研究R上长为N=psn的(1+uβ)-常循环码,其中(n,p)=1,β为R中单位(即β=β0+uβ1+…+uk-1βk-1,其中β0为Fpm中非零元,βi∈Fpm,1≤i≤k-1)。记RN=R[x]/〈xN-(1+uβ)〉。定义μ:RN→Fpm[x]/〈xN-1〉为:∀f(x)∈RN,μ(f(x))=f(x)(modu),则μ是 环 同 态。 记R(v,r)=GR(R,r)[v]/〈-(1+uβ)〉。类似于文献[8]中引理3.1的证明可得下面引理。
引理1 在R(v,r)中,v-1是幂零的,且幂零指数为psk。
定理1 环R(v,r)是有限链环,其极大理想为〈v-1〉,剩余域为。R(v,r)的理想为〈(v-1)i〉,其中0≤i≤psk。
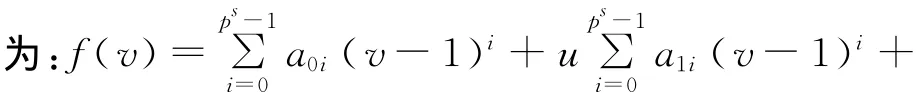
由引理1知u=(v-1)ps β-1,因 此 存 在g(v)∈R(v,r),使得f(v)=a00+(v-1)g(v)。
如果a00=0,则由(v-1)幂零可得f(v)=(v-1)g(v)是幂零的。
如果a00≠0,a00是Fqr的单位,则f(v)=a00+(v-1)g(v)。设h(v)=(v-1)g(v),t=psk,则1=1+ht(v)=(1+h(v))(1-h(v)+h2(v)-…+ht-1(v)),因此f(v)可逆。故f(v)不是可逆的当且仅当a00=0。此时有f(v)∈〈v-1〉,因此R(v,r)是局部环,其极大理想为〈v-1〉。则R(v,r)是有限链环,其极大理想为〈v-1〉,剩余域为,且R(v,r)的 理 想 为 〈(v-1)i〉,其中0≤i≤psk。
推论1 设C是GR(R,r)上长为ps的(1+uβ)-常循环码,则C=〈(v-1)i〉⊆R(v,r),其中0≤i≤psk,且C中码字个数为:
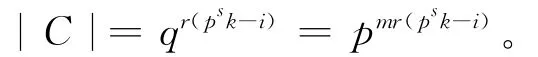
证明 因为GR(R,r)上长为ps的(1+uβ)-常循环码恰好是R(v,r)的理想,故第1部分成立。又因为R(v,r)是有限链环,其剩余域为Fqr,故第2部分成立。
由于R(v,1)=R[v]/〈-(1+uβ)〉,则对∀a∈R(v,1),有a=a0+a1x+…+,其中ai∈R。设∀c∈Rn(v,1),则c=+),其中∈R,0≤i≤ps-1,0≤j≤n-1。定义映射φ:R(v,1)n→RN为:φ(c)=(,…易知φ是环同构映射。
下面一些定理的证明过程类似于文献[8]中相应定理的证明,在这里省略不证。
定理2 码C是R(v,1)上长为n的x-常循环码充要条件为φ(C)是R长为N的(1+uβ)-常循环码。即I是R(v,1)[z]/〈zn-x〉的理想⇔φ(I)是R[x]/〈xN-(1+uβ)〉的理想。
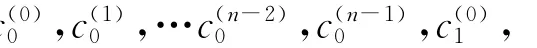
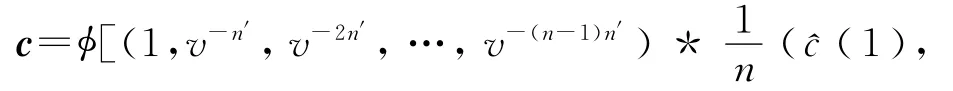
对∀b∈GR(R,r),则b=ξ0+uξ1+…+uk-1ξk-1,其中ξi∈Fqr。
定义GR(R,r)上的Frobenius环自同构σf为σf(b)=++…+uk-1,且可扩展为R(v,ri)上的Frobenius环自同构。对任意c∈RN,则有^ci∈R(v,ri)和^cqi=σf(^ci),其中下标为模n后的值。
设~c= {(^c0,^c1,…,^cn-1)∈R(v,r)n|^ci∈R(v,ri),^cqi=σf(^ci)},则在向量分量加法与分量积运算下~c是环。并且(v,ri)。
定理3 设N=psn,其中(n,p)=1,则γ:RN→R(v,ri):γ(c(x))=(^ci)i∈I,是环同构。特别地,如果C是R上长为N的(1+uβ)-常循环码,则CCi,其中Ci是R(v,ri)中的理想{c(vn′ξi)|c(x)∈C}。
推论2 环R上长为N的不同的(1+uβ)-常循环码的个数为(psk+1)t,其中t为模n的q-分圆陪集的个数。
引理3 设n′是满足nn′≡1(modps+e)的正整数,其中e是使pe≥m成立的最小正整数;设fh是ξh在R[x]中的极小多项式,cq(h,n)是包含h的模n的q-分圆陪集;则有:
(1)如果i∉cq(h,n),则fh(vn′ξi)是R(v,ri)的单位。
(2)fh(vn′ξh)∈〈v-1〉,且fh(vn′ξh)∉〈(v-1)2〉。
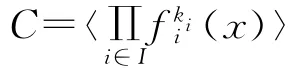
证明 由定理3知CCi,其中Ci是R(v,ri)中的理 想 {c(vn′ξi)|c(x)∈C}。当 0≤ki≤psk时,对于满足Ci=〈(v-1)ki〉的i,定义fi(x)为ξi的极小多项式。则其中fi(x)是[x]中两两互素的首一不可约多项式。由fi(x)的选取知,因此对于c(x)∈C,存在g(x)∈RN,使
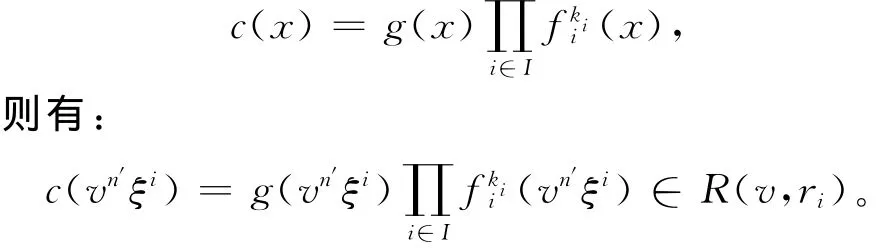

2.2 (1+uβ)-常循环对偶码
设β′=1+u(-β+uβ2+…+(-1)k-1×uk-2βk-1),则β′为R中 可 逆 元 且 (1+uβ)(1+uβ′)=1。因此(1+uβ)-1=(1+uβ′)。设R′N=R[x]/〈xN- (1+uβ′)〉,定 义 映 射η:RN→R′N为:f(x)→f*(x),易知其为环同构。因此只要将前面的fi(x)替换成(x)即可得到R′N中相应的结论。
定理5 设C是RN的理想,则C*={f*(x)|∀f(x)∈C}是R′N的理想。
证明 设λ=1+uβ,则λ-1=1+uβ′。
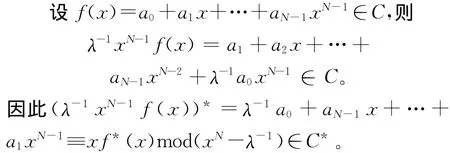
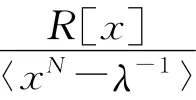
〉的理想。
定理6 设a(x)=a0+a1x+…+aN-1xN-1,b(x)=b0+b1x+…+bN-1xN-1∈RN,a=(a0,a1,…,aN-1),b′=(bN-1,bN-2,…,b0),则在RN中,a(x)b(x)=0⇔a·(b′)=0,其中1≤j≤N。
证明 考虑a(x)b(x)中xh的系数,则
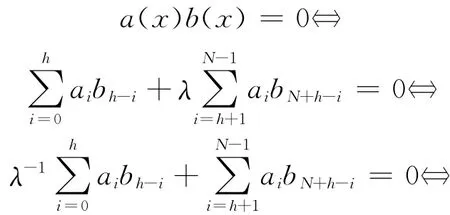
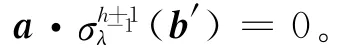
故a(x)b(x)=0⇔a·(b′)=0,其中1≤j≤N。
定理7 设C是R上长为N的λ-常循环码,则C⊥=A(C)*是R′N的理想。
证明 由定理5和定理6知此定理成立。
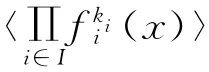
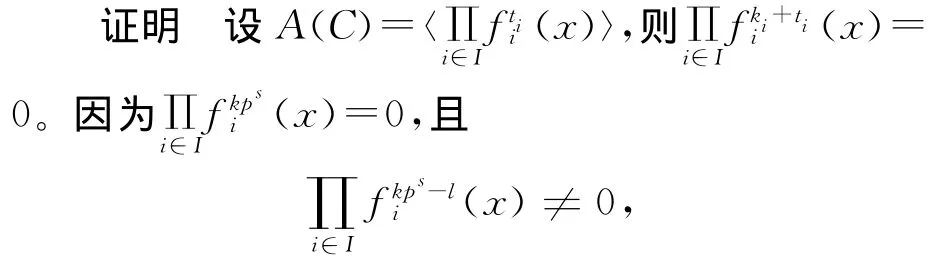
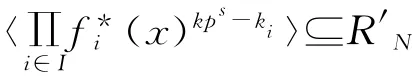
定理9 设CCi是R上长为N的(1+uβ)-常循环码,Di′=C⊥i,其中i′为包含n-i的分圆陪集的代表元,Ci为R(v,ri)的理想,则C⊥=Di⊆R′N。
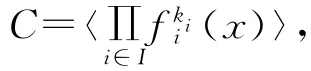
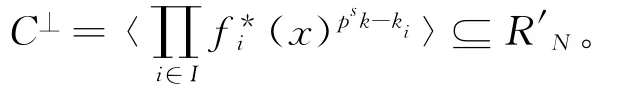
3 结束语
本文主要得到了环Fpm+uFpm+…+uk-1Fpm上任意长的(1+uβ)-常循环码的结构,确定了此环上给定长的不同的(1+uβ)-常循环码的个数及这样的码所含码字的个数,研究了环R上的(1+uβ)-常循环对偶码的结构。
[1]Hammons A R,Kumar P V,Calderbank A R,et al.TheZ4-linearity of Kerdock,Preparata,Goethals,and related codes
[J].IEEE Trans Inform Theory,1994,40(2):301-319.[2]Wolfmann J.Negacyclic and cyclic codes overZ4[J].IEEE Trans Inform Theory,1999,45(7):2527-2532.
[3]Blackford T.Negacyclic codes overZ4of even length[J].IEEE Trans Inform Theory,2003,49(6):1417-1424.
[4]Abualrub T,Oehmke R.On the generators ofZ4cyclic codes of length 2e[J].IEEE Trans Inform Theory,2003,49(9):2126-2133.
[5]Dinh H Q,Lpez-Permouth S R.Cyclic and negacyclic codes over finite chain rings[J].IEEE Trans Inform Theory,2004,50(8):1728-1744.
[6]Dinh H Q.Negacyclic codes of length 2sover Galois rings[J]. IEEE Trans. Inform. Theory, 2005, 51(12):4252-4262.
[7]黄成宝,朱士信.环F2+uF2+u2F2上线性码及其Gray象的生成矩阵[J].合肥工业大学学报:自然科学版,2009,32(9):1436-1438,1441.
[8]Kai Xiaoshan,Zhu Shixin,Li Ping.(1+λu)-constacyclic codes overFp[u]/〈um〉[J].Journal of the Franklin Institute,2010,347:751-762.
[9]Zhu Shixin,Kai Xiaoshan.A class of constacyclic codes overZpm[J].Finite Field and Their Applications,2010,16:243-254.
[10]Zhu Shixin,Kai Xiaoshan.Dual and self-dual negacyclic codes of even length overZ2a[J].Discrete Mathematics,2009,309:2382-2391.
A class of constacyclic codes over ring++…+
LI Yan, ZHU Shi-xin
(School of Mathematics,Hefei University of Technology,Hefei 230009,China)
In this paper,(1+uβ)-constacyclic codes over the ringR=Fpm+uFpm+…+uk-1Fpmof an arbitrary length is studied.The number of distinct (1+uβ)-constacyclic codes over the ringRof lengthN=psnis determined,so is the number of codewords in each such code.The structure of(1+uβ)-constacyclic dual codes over the ringRis also derived.
constacyclic code;Galois ring;dual code;discrete Fourier transform;annihilator
TN911.22
A
1003-5060(2012)03-0408-04
10.3969/j.issn.1003-5060.2012.03.027
2011-06-07
国家自然科学基金资助项目(60973125);高等学校博士学科点专项科研基金资助项目(20080359003)作者简介:李 岩(1985-),男,安徽蒙城人,合肥工业大学硕士生;
朱士信(1962-),男,安徽枞阳人,博士,合肥工业大学教授,博士生导师.
(责任编辑 马国锋)

