基于同伦分析法的一类KdV－Burgers方程的近似解

朋群芳， 郭清伟

（合肥工业大学 数学学院，安徽 合肥 230009）

基于同伦分析法的一类KdV－Burgers方程的近似解

朋群芳， 郭清伟

（合肥工业大学 数学学院，安徽 合肥 230009）

同伦分析方法是解决非线性初值问题近似解的一种非常有效的方法。文章利用同伦分析方法求一类非线性KdV－Burgers方程的近似解，并将所得结果与已有方法所得结果进行比较。研究表明，同伦分析方法不仅计算简单而且结果精确，故同伦分析方法是解非线性KdV－Burgers方程近似解的一种行之有效的方法。

KdV－Burgers方程；同伦分析法；近似解

非线性问题存在于许多科学领域，人们对于非线性问题的研究也越来越重视。近几年来很多的方法用于解决非线性问题，如变分迭代法［1－3］、Adomian分解法［4－5］及同伦摄动法［6－7］等。廖世俊于1992年提出同伦分析法的基本思想，并用该方法处理非线性初值问题的近似解［8－9］。同伦分析方法是基于同伦理论的一种新的解析方法，它在方法上彻底抛弃了小参数假设，从根本上克服了传统摄动法的局限性，在逻辑上包含了其他“非摄动方法”，从而更具一般性，该方法已被成功用于解决数学和工程技术中的许多非线性问题［10－16］。

本文将用同伦分析方法研究一类二次非线性KdV－Burgers方程的近似解，并把所得结果与用改进的Bernstein多项式方法［17］所得的二次非线性KdV－Burgers方程的近似解进行比较。KdVBurgers方程为：

其中，μ1、μ2和μ3均为常数。

1 同伦分析方法简介

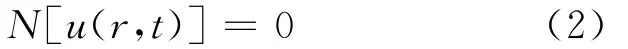
考虑以下一般形式的微分方程：其中，N为非线性算子；u（r，t）为关于r和t的未知函数；r和t为2个相对独立的变量。为了简单起见，忽略边界值和初始条件，由同伦思想，文献［18］得到的零阶变形方程为：

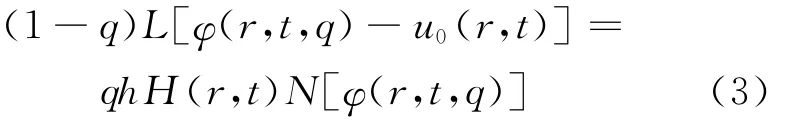
其中，q∈（0，1）为嵌入参数；h为非零的辅助参数；H（r，t）为辅助函数；L为辅助线性算子；u0（r，t）为u（r，t）的 初 始 猜 测 解；φ（r，t，q）为 未 知的函数。

显然，当q＝0和q＝1时，分别有φ（r，t，0）＝u0（r，t）和φ（r，t，1）＝u（r，t），因此，当q从0变到1时，φ（r，t，q）就从初始猜测值u0（r，t）变到微分方程的解u（r，t）。

由Taylor定理，可将φ（r，t，q）展开成q的幂级数，即

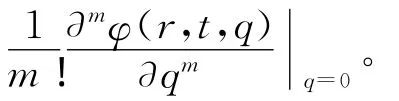
取H（r，t）＝1，（3）式变为：

为方便，定义向量um－1（r，t）＝｛u0（r，t），u1（r，t），…，um－1（r，t）｝，

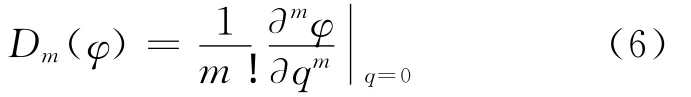
将（5）式两边分别对q求m阶偏导，再令q＝0，最后两边除以m！，则得到m阶变形方程为：

将（4）式代入（8）式得：

这样，当m≥1时，um（r，t）就可以由（7）式求出。

2 同伦分析解

将运用同伦分析方法求方程（1）的近似解。为方便应用，先介绍以下定理。

定理1 若φ（r，t，q）如（4）式定义，Dm（φ）如（6）式定义，则

证明见文献［16］。

推论1 由定理1，有：

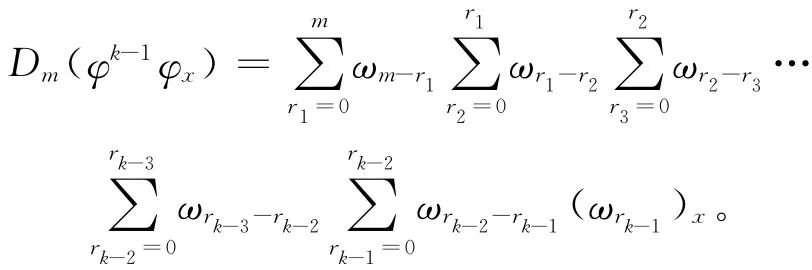
由方程（9）、（11）和推论1有：

假设（x，t）是方程的一个特解，即

则由m阶变形方程（7）和初始条件um（x，0）＝0（m≥1），可得：

对于方程（1），取初始值

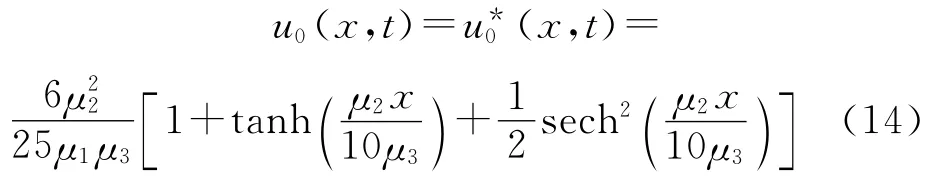
已有学者给出方程（1）的精确解［19－20］为：

3 算 例

例1 求解方程（1），其中μ1＝0.01，μ2＝1，μ3＝100。

考虑方程的二阶近似解U2（x，t）。首先来考察h对U2（x，t）收敛的影响，为方便，令f＝U2，g＝（U2）xt，s＝（U2）xxtt。

当x＝1，t＝1时，U2－h、（U2）xt－h、（U2）xxtt－h曲线如图1所示。

图1 例1的h曲线

由图1可看出，－5≤h≤5为h的有效区域。取h＝－1，本文得到近似解U2（x，t）与精确解以及文献［17］中的结果进行比较，见表1所列，结果表明，同伦分析法只需要进行很少的步骤就可得到很精确的结果。当t＝0.8，t＝2.0时近似解与精确解的误差如图2所示。

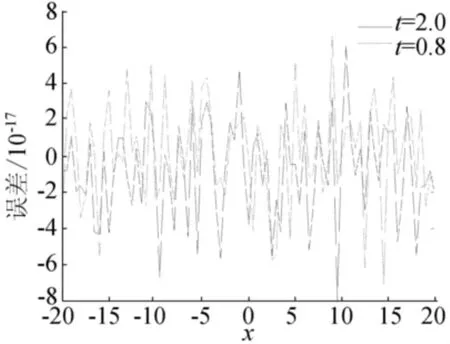
图2 U2（x，t）的误差

例2 求解方程（1），其中μ1＝1，μ2＝1，μ3＝1。

本文考虑方程的三阶近似解U3（x，t），首先考察h对U3（x，t）收敛的影响，为方便，令f＝U3，g＝（U3）xt，s＝（U3）xxtt，当x＝1，t＝1时的U3－h、（U3）xt－h、（U3）xxtt－h曲线如图3所示。

由图3可知，－2≤h≤0为h的有效区域。取h＝－1，本文得到近似解U2（x，t）与精确解以及文献［17］中的结果进行比较，见表2所列，结果表明，同伦分析法只需要进行很少的步骤就得到很精确的结果。近似解与精确解的绝对误差如图4所示。

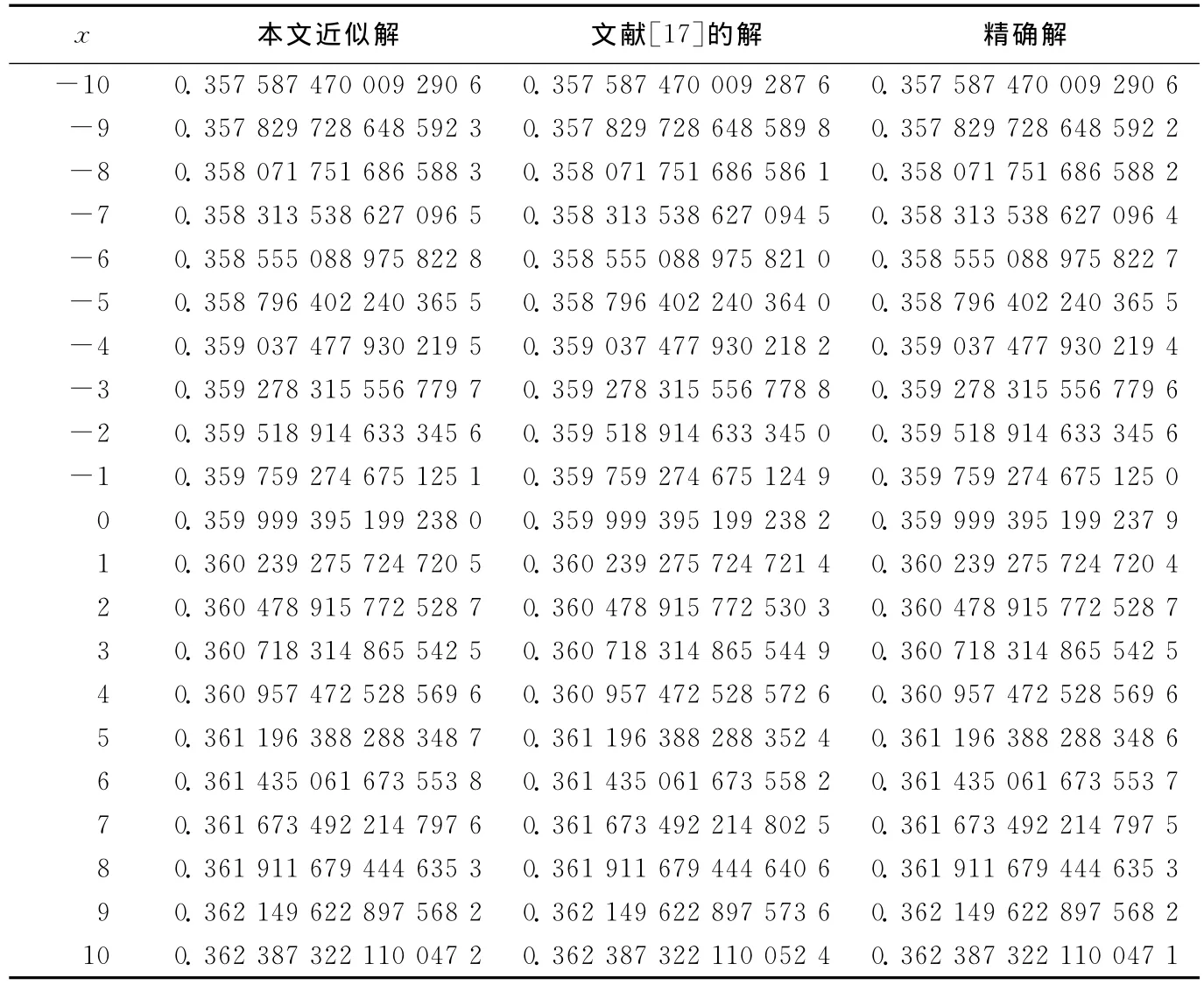
表1 当t＝1.05时例1近似解与精确解的比较

图3 例2的h曲线

图4 例2的U3（x，t）绝对误差

表2 例2近似解与精确解的比较

例3 求解方程（1），其中μ1＝1，μ2＝－2，μ3＝1。

考虑方程的三阶近似解U3（x，t），考察h对U3（x，t）收敛的影响，为方便，令f＝U3，g＝（U3）xt，s＝（U3）xxtt，当x＝1，t＝1时的（U3）xt－h、（U3）xt－h、（U3）xxtt－h曲线如图5所示，由图5可看出，－1.1≤h≤－0.7为h的有效区域。取h＝－1，t＝0.1时近似解与精确解以及误差见表3所列。当t＝0、1.5、3时，本文方法得到的误差与文献［17］得到的误差如图6、图7所示，结果表明，本文方法不仅计算步骤少而且精确。

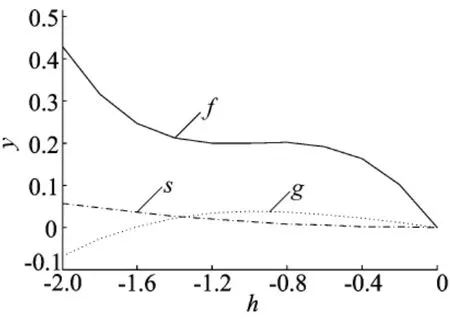
图5 例3的h曲线

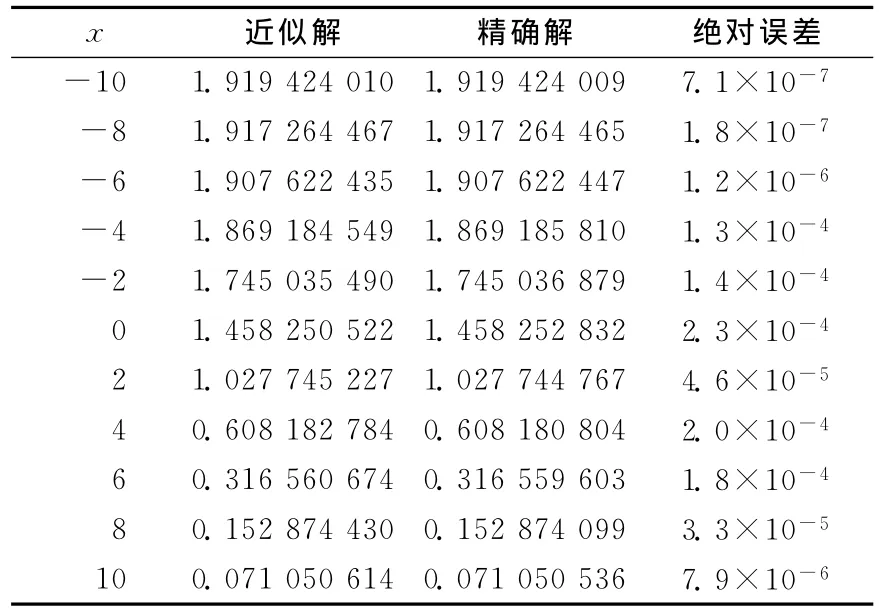
表3 当t＝0.1时例3近似解与精确解的比较

图6 例3的U3（x，t）误差

图7 文献［17］的误差

4 结束语

本文利用同伦分析法，求解了一类非线性KdV－Burgers方程，得到其近似解，该解与精确解吻合很好，并与文献［17］中的结果进行比较，研究发现，该方法不仅计算简单，并且效率很高。该方法可借助计算机代数系统如Matlab或Maple等软件快速高效地完成，能够方便地用于求解非线性演化方程的高精度近似解析解。随着研究的深入，同伦分析法的理论体系必将日趋完善，从而在非线性科学的研究中发挥更加重要的作用。

［1］Darvishi M T，Khani F，Soliman A A.The numerical simulation for stiff systems of ordinary differential equations［J］.Computers and Mathematics with Applications，2007，54：1055－1063.

［2］Darvishi M T，Khani F.Numerical and explicit solutions of the fifth－order Korteweg de Vries equations［J］.Chaos，Solitons ＆Fractals，2009，39：2484－2490.

［3］He Jihuan.Variational iteration method－a kind of non－linear analytical technique：some examples［J］.International Journal of Non－Linear Mechanics，1999，34：699－708.

［4］Adomian G，Rach R.Modified decomposition solution of linear and nonlinear boundary－value problems［J］.Nonlinear Anal，1994，34：615－619.

［5］梁小磊.非线性偏微分方程及其数值计算［D］.合肥：合肥工业大学，2010.

［6］He Jihuan.Homotopy perturbation method［J］.Computer Methods in Applied Mechanics and Engineering，1999，178：257－262.

［7］He Jihuan.Homotopy perturbation method：a new nonlinear analytical technique［J］.Applied Mathematics and Computation，2003，135：73－79.

［8］Liao Shijun.On the homotopy analysis method for nonlinear problems［J］.Applied Mathematics and Computation，2004，147：499－513.

［9］廖世俊.同化分析方法：一种新的求解非线性问题的近似解析方法［J］.应用数学和力学，1998（10）：885－890.

［10］Liao Shijun.On the analytic solution of magnetohydrodynamic flows of non－Newtonian fluids over a stretching sheet［J］.Fluid Mechanics，2003，488：189－212.

［11］Darvishi M T，Khani F.A series solution of the foam drainage equation［J］.Computers and Mathematics with Applications，2009，58：360－368.

［12］Abbasbandy S，Shirzadi A.A new application of the homotopy analysis method：solving the Sturm－Liouville problems［J］.Communications in Nonlinear Science and Numerical Simulation，2011，16：112－126.

［13］Alomari A，Noorani M S，Nazar R.On the homotopy analysis method for the exact solutions of Helmholtz equation［J］.Chaos，Solitons ＆ Fractals，2009，41：1873－1879.

［14］Yue Tan，Abbasbandy S.Homotopy analysis method for quadratic Riccati differential equation ［J］.Communications in Nonlinear Science and Numerical Simulation，2008，13：539－546.

［15］Bataineh A S，Noorani M S.Modified homotopy analysis method for solving systems of second－order BVPs［J］.Communications in Nonlinear Science and Numerical Simulation，2009，14：430－442.

［16］Molabahrami A，Khani F.The homotopy analysis method to solve the Burgers－Huxley equation［J］.Nonlinear Analysis：Real World Application，2009，10：589－600.

［17］Dambaru B.Use of modified Bernstein polynomials to solve KdV－Burgeres eqution numerically［J］.Applied Mathematics and Computation，2008，206：457－464.

［18］廖世俊.超越摄动－同伦分析方法导论［M］.北京：科学出版社，2007：13－19.

［19］Jeffrey A，Mohamad M.Exact solutions to the Kortewegde Vries－Burgers equation ［J］.Wave Motion，1991，14：369－375.

［20］Demiray H.A note on the exact travelling wave solution to the KdV－Burgers equation ［J］.Wave Motion，2003，38：367－369.

Approximate solution of KdV－Burgers equation based on homotopy analysis method

PENG Qun－fang， GUO Qing－wei
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

The homotopy analysis method（HAM）is effective for solving the approximate solution of nonlinear initial value problem.In this paper，the HAM is applied to obtaining the approximate solution of nonlinear KdV－Burgers equation，and the result is compared with that solved by the existing method.It shows that the HAM is an effective method to obtain the approximate solution of nonlinear KdV－Buegers equation with convenience and correctness.

KdV－Burgers equation；homotopy analysis method（HAM）；approximate solution

O241.82

A

1003－5060（2012）03－0424－05

10.3969／j.issn.1003－5060.2012.03.031

2011－05－27

安徽省自然科学基金资助项目（11040606M06）；安徽省高等学校省级自然科学研究资助项目（2011AJZI0071）

朋群芳（1986－），女，安徽安庆人，合肥工业大学硕士生；

郭清伟（1968－），男，安徽淮北人，博士，合肥工业大学副教授，硕士生导师.

（责任编辑 闫杏丽）