导航电文星历参数对卫星轨道精度的影响①

周 昀，黄智刚，王陆潇

（北京航空航天大学，北京100191）

0 引 言

卫星导航定位的关键是获知导航卫星发射测距信号时的精确位置，而卫星的轨道信息即星历参数是以导航电文的形式发播给用户，用户通过接收卫星信号，获取包括星历数据在内的导航电文，才能够计算出卫星位置，从而确定用户自身位置。因此导航电文中星历参数质量的好坏直接决定卫星轨道的精度，进而影响到定位精度。

全球卫星导航系统（GPS、GLONASS、GALILEO等）播发的导航电文，特别是卫星星历参数选择和结构设计均有所差异，GPS／GALILEO广播星历参数的设计利用了轨道摄动特征，选取开普勒轨道根数作为广播星历参数，GLONASS卫星轨道则选取卫星位置和速度向量以及太阳和月亮的摄动加速度等参数［1]。

现代化的GPS L2C和L5频点上的CNAV、L1C频点播发的CNAV－2相比NAV电文星历参数也做了改进，改进后的星历参数表示精度更高，参数选择更加合理，改进后的星历参数能精确地表征卫星在轨信息。

具体分析GPS改进前后导航电文中星历参数对其卫星轨道精度的影响，介绍了不同频点播发的广播星历参数的拟和算法，分析了其帧结构设计的一些改进。

1 卫星轨道精度分析

导航电文中卫星星历是描述卫星运行轨道的信息，卫星星历按精度可分为两种，广播星历和精密星历。广播星历是由美国系统跟踪站观测数据计算出的卫星轨道外推得出的，即RINEX文件，并由卫星实时向用户发播，其精度较低，一般在m级。而精密星历采用地区乃至全球跟踪站观测资料计算出的卫星轨道，主要用于事后处理。目前精度最高的是由国际地球动力学服务组织（IGS）提供的精度星历，其误差一般小于5cm.其中，广播星历参数包括基本开普勒轨道参数和一些摄动系数，由上述参数可以计算卫星在地心地固坐标系中的位置。

受各种摄动的影响，卫星实际轨迹为其理论椭圆轨道附近波动的不规则曲线，而且使得描述其轨道的开普勒根数是随时间变化的函数。为了更好地理解导航定位系统中卫星轨道的描述和分析研究，将卫星轨道区分为“实际轨道”、“预报轨道”和“广播轨道”，如图1所示。

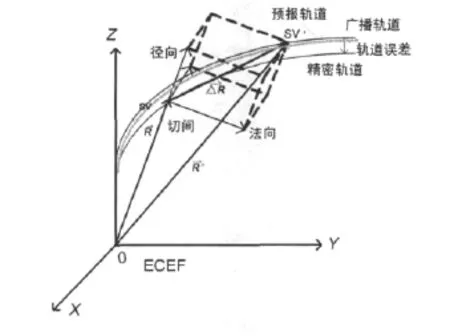
图1 卫星轨道模型以及轨道误差矢量分解

实际轨道描述了卫星在轨真实运行状态，由于IGS提供所有GPS卫星每15min的三维轨道坐标，具有很高的精度，因此，将IGS精密星历给出的卫星在国际地球参考框架（ITFR）系下的轨道坐标作为实际轨道（不考虑坐标框架的转换误差［3]），如图1中的精密轨道。而预报轨道则根据参考时间之前的精密轨道信息和卫星受力模型预测得到，如图1中的预测轨道。由于卫星受力的复杂性，预报轨道和精密轨道总有一定的误差。换言之，预报轨道不可能准确无误的反应卫星真实的在轨信息，总有一定的偏差和扰动，即图1中的差值。实际上，将预报轨道曲线拟合为一系列开普勒轨道参数，并在导航电文中播发出去。如GPS L1频点上的NAV电文中的15个开普勒轨道参数（toe除外），L2C和L5频点上播发的CNAV电文中，则播发了17个轨道参数（toe除外），具体参数见下文分析。根据导航电文中广播星历参数计算所得的轨道我们称之为广播轨道，即图1中的广播轨道.由于曲线拟合误差，广播轨道和预报轨道也存在一定的偏差，即拟合误差（Fitting Error）（cm 级）。而将广播轨道和IGS精密轨道之间的误差称之为广播轨道误差（一般在m级），如图1中轨道误差的值。

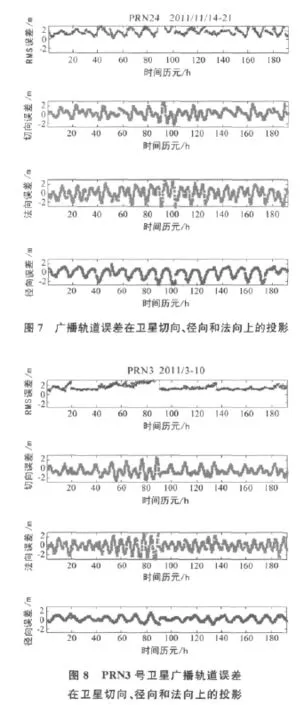
某一历元参考时刻，由精密星历（IGS）得到的卫星地心地固坐标系（ECEF）中实际位置矢量记为R，由同一时刻广播星历参数（RINEX）计算的同坐标系下位置矢量记为R′，ΔR＝R′－R即为广播轨道误差矢量，将该误差矢量投影到三个方向，分别为同时刻卫星径向Rad、切向Alt和法向Act，研究三个方向上广播轨道误差的变化规律，具体矢量分解由图1中所示。

以2010－11－14日、11－15日，PRN＝1－32（除4，15号星外，原因是RINEX文件中没有PRN4和PRN15某些时间段内的广播星历参数，故不予考虑。）为例，仿真分析全天0∶0∶0－23∶45∶00时间段内由导航电文中广播星历参数计算所得的各颗GPS卫星广播轨道误差。仿真结果如图2和图3所示，其中X轴表示历元时刻，即0∶0∶0－23∶45∶00，Y轴表示卫星PRN序号，Z轴则反应均方误差值（RMS）。

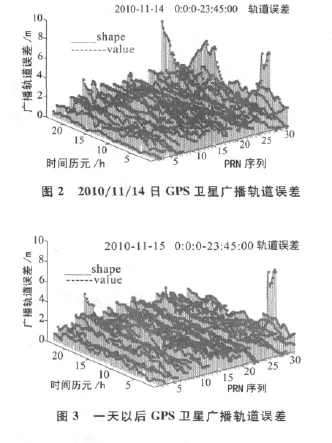
从图2中可以看出，除PRN27号卫星在5－6点，15－18点，22－24点轨道误差超过8m以外，其余卫星一天内广播轨道误差均在3m左右。图3则反应一天以后各颗卫星的轨道误差变化情况，由图可知，同样，除了PRN27号卫星在5－6点轨道误差超过8m，其余卫星一天内广播轨道误差均在3m左右。

为了更好地分析轨道误差长期变化情况，仿真了一周以后（即2010－11－21日）各颗卫星全天0：0：0－23：45：00时间段内广播误差。具体结果如图4所示。

图4 一周以后GPS卫星广播轨道误差

由图4可知，一周之后，卫星广播轨道误差变化规律基本相同，即除PRN27号星误差较大外，其余卫星广播轨道误差均在3m左右。

观察图2到图4广播轨道误差波形变化，发现该误差波形具有一定的周期性和波动性，具体以PRN24号卫星为例，分析其在一周内的变化情况（即2010－11－14日到21日）。仿真结果如图5所示。

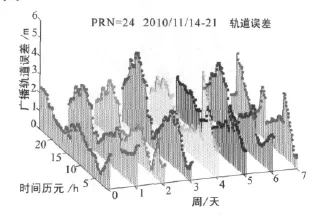
图5 一周内GPS卫星广播轨道误差波形变化

X轴表示历元时刻，即0∶0∶0－23∶45∶00，Y 轴“0”表示周日，即14日这天，“7”表示下个周日，即21日这天，Z轴则表示PRN24号卫星一周内的均方误差值（RMS）.由图5明显可知，一周内该卫星的广播轨道误差在一天的某个时间段内呈现相同的规律，如在每天的15点左右，误差总是较小，在22点左右，误差总是较大。即表现出了一定的周期性。接下来将误差矢量投影到ECEF三个轴上，分析其误差变化情况。

在ECEF框架下，三个坐标轴上误差投影坐标为ΔX、ΔY、ΔZ，以PRN24号星在14日到21日192小时为例，仿真分析其变化特性，具体结果如图6所示。

Z轴投影值，具有明显的余弦周期性变化，其周期与GPS轨道周期（11hr 58m）大体相同。而X和Y轴的投影值余弦变化则并不明显。

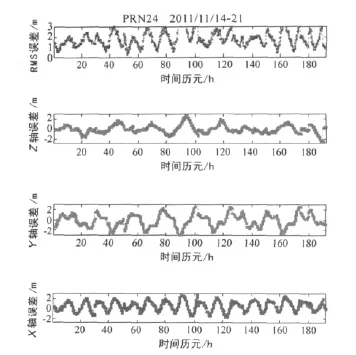
图6 广播轨道误差在X，Y，Z轴上的投影

从卫星运动的切向、法向和径向分析其广播轨道误差向量的变化特性。即将误差矢量ΔR＝R′－R投影到这三个方向，从而确定其模值的变化规律。仍以PRN24号星为例，计算其在14日到21日192小时内各投影方向的误差变化。如图7所示，均方根（RMS）误差大小等于误差矢量的模

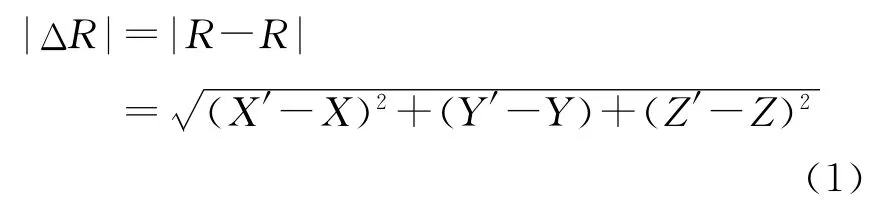
由图7，误差矢量ΔR在三个方向的投影误差具有明显的周期变化特性，且呈现出近似正余弦波形，三个方向的周期T都约等于11hr 58m，与GPS卫星轨道周期基本相同。

为了说明结论的普遍性，分析不同卫星在不同时间段内的广播轨道误差变化特性，现以PRN3号卫星，在3－10日192小时内误差变化为例说明，仿真结果如图8所示。

由图可知三个方向的周期T也约等于11hr 58m，与GPS卫星轨道周期基本相同。

综合分析以上研究结论，用数学模型来反应GPS卫星的广播轨道误差变化特性。设

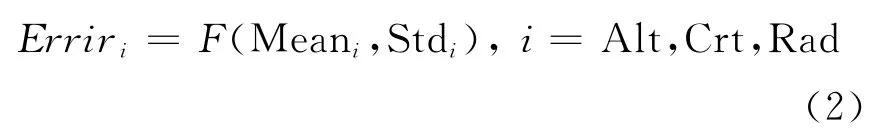
在切向，法向和径向表示如下

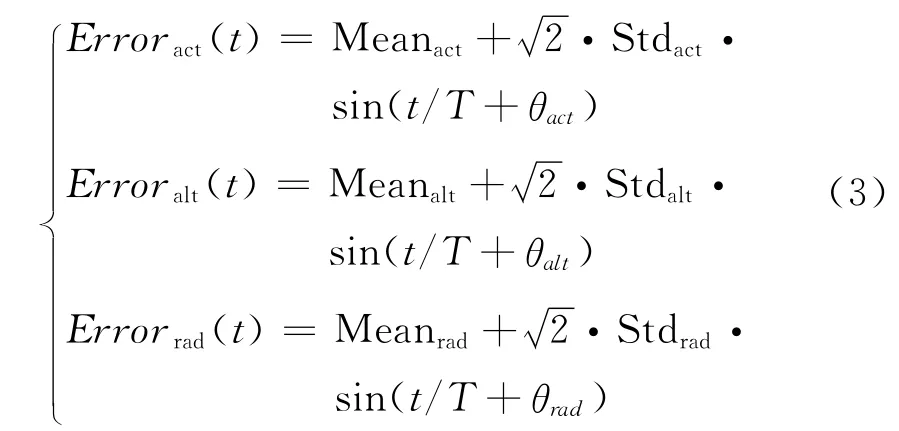
其中：θi为初始相位；T为GPS卫星轨道周期，即11hr 58m.在GPS周内统计各颗卫星在切向、径向和法向的误差分量，即可得其对应均值Mean和方差Std值，从而确定误差方程。

以2011－11－14 至 2011－11－21日为统计时间段，PRN1－32（除PRN4和PRN15外）号卫星误差值为样本空间，统计得到结果表1所示。

表1 广播轨道误差的均值和方差

上述GPS广播轨道误差模型，可用于在建的GNSS（全球导航卫星系统）导航系统星座仿真设计以及导航电文广播星历参数对卫星轨道精度影响的评估研究中。

2 精密星历计算广播星历参数—Brdc15

由精密星历计算广播星历参数的方法是将IGS星历作为观测值，选取一组参数（分别取15个和17个轨道参数，参照ICD－200D和ICD－705），将三维坐标表示成这些参数的函数，依据最小二乘原理估计出一段弧内某一时刻的参数值［2，4]。

用 X（tk），Y（tk），Z（tk）表示tk时刻卫星在地心地固坐标系中的坐标，根据广播参数计算出其位置坐标公式为

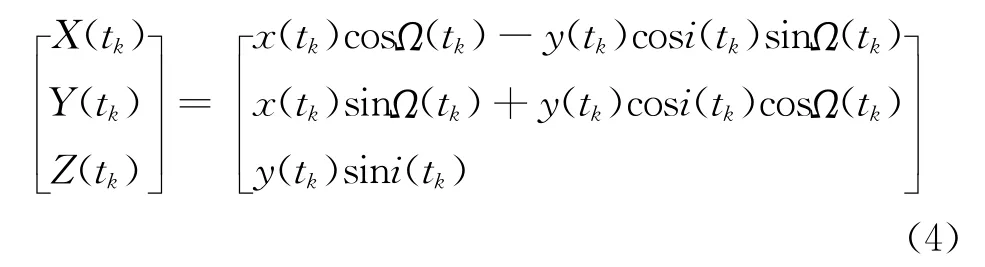
式中：

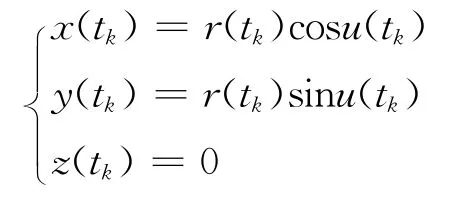
表示卫星在轨道坐标系中的位置，其余参数和算式参照ICD－200D.

令向量

公式（4）变换为以下形式

式中：

卫星坐标矢量R和15个轨道参数的函数关系设为

式中：

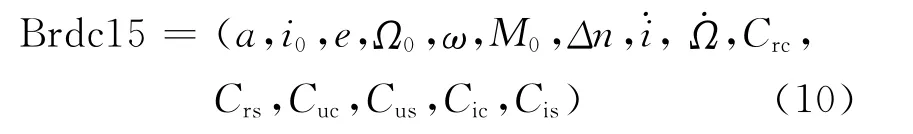
将精密星历（IGS）卫星坐标作为已知量，每15 min取一组值，共取相邻的n（n＝9对应2小时星历，即RINEX文件中时间间隔）个历元的卫星三维坐标，利用最小二乘原理估计轨道参数［4]。得

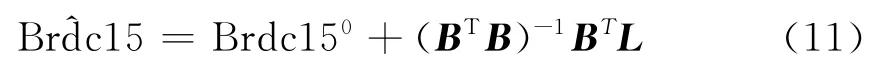
式中：Brdc150表示 Brdc15的近似值；Br＾dc15表示Brdc15的估计值。L＝R－F（Brdc150）表示观察误差。

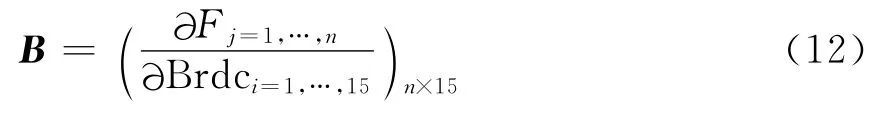
B表示位置矢量对15个轨道参数的偏导数，R＝（X，Y，Z）T表示卫星三维位置，R0＝F（Brdc150）表示由Brdc150计算得到的卫星位置近似值。具体可以由式（1）求出。

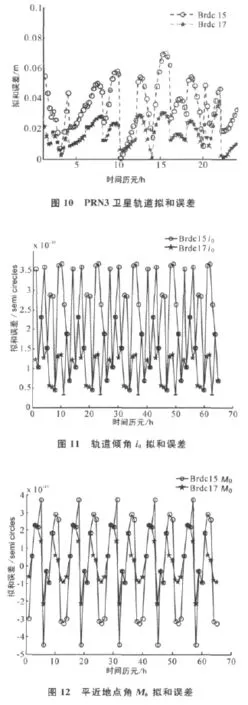
采用2010／11／14－17日三天IGS精密星历文件，n取9，最小二乘拟和PRN3和PRN24两颗卫星在三天内的广播星历参数Brdc150，根据上述计算卫星位置公式，利用拟和所得的轨道参数，计算出卫星位置，并与同时刻RINEX广播星历计算所得卫星位置比较，仿真分析其拟和误差，如图9和图10所示。由图可知，PRN24号卫星拟和误差最大值为9cm，均值在5cm左右，PRN3号卫星拟和误差最大值为7cm，均值在3cm左右，都远远小于上文中广播轨道误差（2～4m），说明该方法可用于广播星历轨道参数的确定。图11和图12则具体分析了基本轨道参数i0（轨道倾角）和M0（平近点角）的拟和误差。

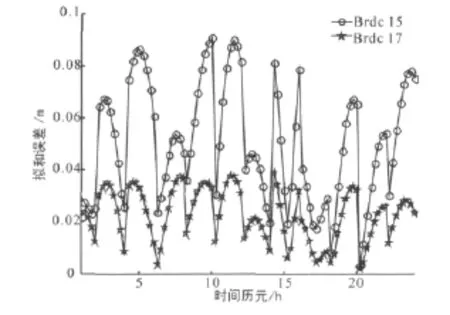
图9 PRN24卫星轨道拟和误差

3 精密星历计算广播星历参数—Brdc17

相比 NAV 电文轨道参数，CNAV／CNAV－2电文在原来的15参数的基础上增加了两项，计算卫星位置的公式也有所变化，分析知计算公式的不同与参数的变化一一对应（图13），但基本原理还是利用开普勒轨道参数外加摄动系数确定卫星位置。为了区别，Brdc15表示NAV电文中15个开普勒轨道参数，（toe已知），Brdc17表示 CNAV／CNAV－2电文中播发的17个轨道参数（toc已知）。

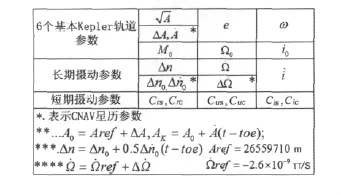
图13 NAV和CNAV中广播星历参数比较

与计算Brdc15参数一样，Brdc17也可以由一系列卫星坐标通过最小二乘拟合得到。利用Brdc17计算卫星在ECEF中坐标公式与式（1）相同。同理，令Rn＝（X，Y，Z）T，卫星坐标矢量Rn和17个轨道参数的函数关系设为：Rn＝Fn（Brdc17），其中 Brdc17＝（ΔA，i0，e，Ω0，ω，M0，Δn0，Crc，Crs，Cuc，Cus，Cic，Cis）

精密星历（IGS）卫星坐标作为已知量，每15 min取一组值，共取相邻的m（取奇数）个历元（m＝9对应2小时星历，即RINEX文件中时间间隔）的卫星三维坐标，利用最小二乘原理估计轨道参数。

其中Brdc170表示Brdc17的近似值，Br＾dc表示Brdc17的估计值，表示位置矢量对17个轨道参数的偏导数，Ln＝Rn－Fn（Brdc170），Rn＝（X，Y，Z）T表示卫星三维位置，＝Fn（Brdc170）表示由Brdc170计算得到的卫星位置近似值，相比Brdc15，Bn有所不同，增加的偏导数有

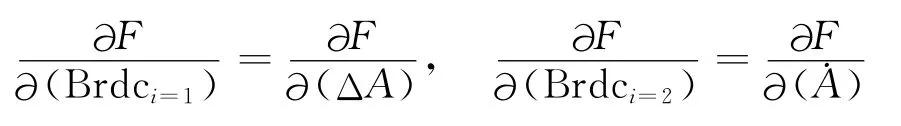
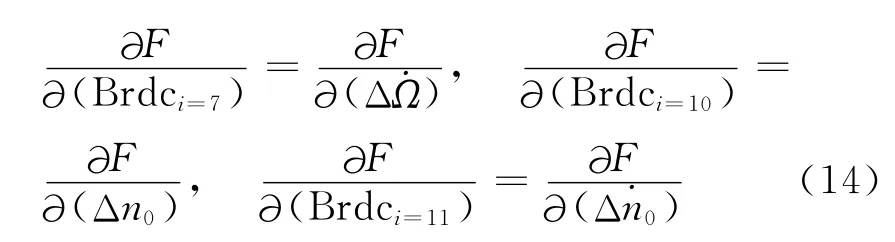
与拟和Brdc15一样，同样采用2010年11月14－17日三天IGS精密星历文件，n取9，最小二乘拟和PRN3和PRN24两颗卫星在三天内的广播星历参数Brdc17，拟和误差如图9和图10所示。由图可知，PRN24号卫星拟和误差最大值为4cm，均值在2cm左右，PRN3号卫星拟和误差最大值为4cm，均值在1.5cm左右，都远远小于第一部分中广播轨道误差（2～4m），说明该方法同样可用于确定广播星历轨道参数Brdc17.图11和图12则同样示出了基本轨道参数i0和M0的拟和误差，相比Brdc15中的i0和M0，拟和误差的幅值更小，这与图9和图10中的结果是对应的。

4 GPS导航电文星历参数帧结构

L1频点NAV电文由超帧，主帧和子帧组成，每个子帧为固定的300bit，广播星历参数分成两部分，在子帧2和子帧3内广播，其总数据量为358bits.具体参数位置如图14所示。

L5和L2C频点上CNAV电文结构采用300 bit固定长度的基本帧（即数据块）结构，广播星历参数在数据块类型10和11中广播，其总数据量为432bits.

L1C频点CNAV－2电文由三个子帧组成，星历参数在第二子帧（帧长600bit）内，总数据量421 bits.

比较可知，三种电文星历参数都是基于开普勒轨道模型，CNAV将轨道半长轴和平均角速度看作随时间变化的变量，即增加了两个表示变化率的参数。除此之外，CNAV数据的精度相比NAV均有所提高，所以总数据量相应地增加了63bit（只考虑CNAV中一个toe值）。而CNAV－2星历参数内容与精度与CNAV完全相同，不同之处在于星历参数在一个帧内播发，有利于接收机得到一帧数据后能立即解算卫星位置，而不需要等待直至接收到下一帧星历数据，从而在一定程度上提高接收机首次定位时间（TTFF）.此优势与CNAV－2电文采用的LDPC（低密度奇偶校验码）＋交织编码以及数据传输速率是密切相关的。

图14 NAV、CNAV、CNAV－2中广播星历参数帧结构比较

5 结 论

综合分析GPS导航电文中星历参数对卫星轨道精度的影响，得出以下结论：

1）GPS卫星广播轨道误差在一周内大约在2～4m内变化（除PRN27号卫星外），而其在切向、径向和法向的投影值呈现周期性余弦变化，其演变周期与GPS轨道周期近似相等，约为11hr 58m.

2）选取17个广播轨道参数表示的星历数据相比15个参数，其轨道拟和误差值大约改进2～3cm.

3）研究得出的GPS广播轨道误差模型以及星历参数的改进可用于在建的导航系统星座仿真以及星历参数的设计研究。

［1]胡松杰.GPS和GLONASS广播星历参数分析及算法［J].飞行器测控学报，2005（3）：37－42.

［2]程义军.基于IGS精密星历的GPS卫星轨道分析［D].武汉：武汉大学，2005.

［3]崔先强.两种GPS广播星历参数算法的比较［J].空间科学学报，2006，26（5）：382－387.

［4]孙海燕，程义军.通过IGS精密星历反算GPS卫星的瞬时轨道参数［J].全球定位系统，2005，30（增）：25－27.