关于序半群的正则和反强正则同余

谢祥云，谷泽



关于序半群的正则和反强正则同余

谢祥云，谷泽

（五邑大学 数学与计算科学学院，广东 江门 529020）

引入了序半群中反拟链和反强正则同余等概念，讨论了它们的一些性质，给出了正则同余和反强正则同余的一般刻画.

反拟链；反强正则同余；正则同余

1 引言与预备知识

本文用到的其他定义和术语参见文献[12-13].

2 正则和反强正则同余

由性质1，有推论1.

.

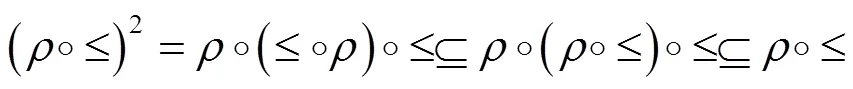
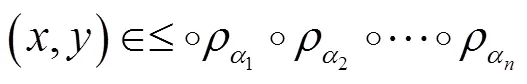
3 正则和反强正则同余的刻画

为给出正则和反强正则同余的一般刻画，先给出定义3.

证明 1）、2）容易证明，我们仅证明3）.

我们仅证A），用同样的方法可证B）、C）、D）.

充分性的证明与必要性类似，证略.

证明 必要性.由引理1及定义2，显然.

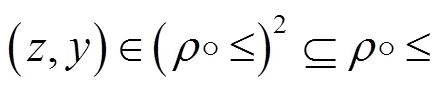
[1] FUCHS L. On group homomorphic images of partially ordered semigroups[J]. Acta Sci Math, 1964, 25: 139-142.

[2] MCCORTHY P J. Homomorphisms of certain commutative lattice-ordered semigroup[J]. Acta Sci Math, 1966, 27: 63-65.

[3] BLYTH T S, JANOWI M F. Residuation theory[M]. Oxford: Pergamon Press, 1972.

[4] XIE Xiangyun. Contributions to theory of congruences on ordered semigroups[D]. Lanzhou: Lanzhou University, 1995.

[5] XIE Xiangyun. On regular, strongly regular congruences on ordered semigroups[J]. Semigroup Forum, 2000, 61(2): 159-178.

[6] KEHAYOPULU N, TSINGLIS M. On subdirectly irreducible ordered semigroups[J]. Semigroup Forum, 1995, 50: 161-177.

[7] KEHAYOPULU N, TSINGLIS M. Pseudoorder in ordered semigroups[J]. Semigroup Forum, 1995, 50: 389-392.

[8] XIE Xiangyun. Regular congruence classes of ordered semigroups[J]. J Math Res Exposition, 2001, 21(2): 207–211.

[9] XIE Xiangyun, SHI Xiaoping. Order-congruences on S-posets[J]. Commun Korean Math Soc, 2005, 20(1): 1-14.

[10] XIE Xiangyun, WU Mingfen. On congruences on ordered semigroups[J]. Math Japan, 1997, 45(1): 81-84.

[11] XIE Xiangyun, SHI Xiaoping. A note of order congruences on ordered semigroups[J]. J Math Res Exposition, 2008, 28(4): 898–904.

[12] HOWIE J M. An introduction to semigroup theory[M]. London: Acad Press, 1976.

[13]谢祥云. 序半群引论[M]. 北京：科学出版社，2001.

On Inverse Strongly Regular Congruences on Ordered Semigroups

XIEXiang-yun, GUZe

(School of Mathematics and Computation Science, Wuyi University, Jiangmen 529020, China)

In this paper, inverse quasi-chain and inverse strongly regular congruences on ordered semigroups are introduced. Some of their properties are studied, and some theorems are given to characterize regular congruences and inverse strongly regular congruences.

inverse quasi-chain; inverse strongly regular congruences; regular congruences

1006-7302（2012）01-0001-05

O152. 7

A

2011-07-26

国家自然科学基金资助项目（No.10961014）；广东省科技计划资助项目（2010B010600039）；广东省自然科学基金资助项目（S201101000368）

谢祥云（1964—），男，安徽舒城人，教授，博士，硕士生导师，研究方向为序半群的代数理论、模糊代数、粗糙集理论.