T700/9916复合材料层合板恒温吸湿行为研究

曹 素， 王 波， 矫桂琼

（西北工业大学力学与土木建筑学院，西安 710129）

碳纤维增强树脂基复合材料（CFRP）由于具有较高的比强度和比刚度，较好的可设计性和抗疲劳断裂性能，已成为航空航天飞行器结构件中的重要材料［1］。然而，不论是未增强的树脂还是树脂基复合材料都能从周围环境中吸收水分，被吸入的水分可能引起材料的膨胀，特别是在较高温度情况下，可能软化和减弱基体和基体/纤维界面，因此吸湿行为对材料的力学性能有很大的危害［2］。了解碳纤维增强树脂基复合材料的吸湿过程，确定材料的吸湿量和内部水分分布，对研究材料的老化过程以及预测构件的服役寿命极其重要。

大量研究表明［3～6］，CFRP 材料吸湿行为的主要机制是水分扩散过程，吸湿过程主要受环境温度和相对湿度的影响，其中材料的饱和吸湿量与环境的相对湿度有关，而扩散系数的变化则依赖环境温度。Shen C H和Springer G S［7］提出的一维Fick扩散模型在忽略侧面吸湿的前提下，可用于根据实验值求得扩散系数和吸湿动力学曲线。国内外已有学者［8，9］使用有限元模拟软件 ABAQUS对 CFRP薄板的吸湿行为进行模拟，模拟结果与实验值吻合较好，验证了ABAQUS软件模拟纤维复合材料吸湿行为的可行性。

由于复合材料层合板的各向异性特征，以及碳纤维不吸湿而基体吸湿，用传统实验方法确定材料的扩散率和饱和吸湿量周期较长，并且难以得到材料内部的水分分布情况。因此，本研究根据ASTM D 5229/D 5229M—1992（2004）标准［10］对 CFRP 层合板T700/9916在70℃恒温水浴和70℃相对湿度为98%，91%，84%恒温恒湿环境箱中进行吸湿实验。根据实验结果，使用插值法和有限元模拟软件ABAQUS算得扩散系数和饱和吸湿量，并对各湿度条件下材料的吸湿行为进行模拟，获得吸湿动力学曲线以及水分分布情况。

1 实验

1.1 材料

实验采用T700/9916碳纤维增强树脂基复合材料层合板，铺层方式为［+45/0/-45/90］4S，纤维体积分数为65%。试样尺寸为100mm×30mm×4mm，未采用ASTM D 5229/D 5229M—1992（2004）标准推荐的试样厚度，主要是为了研究在各表面均参与吸湿情况下复合材料层合板的吸湿行为。

1.2 吸湿实验

本实验过程参照 ASTM D 5229/D 5229M—1992（2004）标准《聚合物基复合材料吸湿性能和浸润平衡的标准实验方法》［10］。在进行吸湿实验前，先将试样放置于60℃烘箱（电热恒温鼓风干燥箱，DGG-9076A）内进行烘干到相对平衡干态（间隔24h的质量变化小于0.01%）。并记录烘干试样质量（Wb），作为吸湿过程的基准质量。将烘干后的试样，分别放置于温度为70℃的纯净水（电热恒温三用水箱，Cr42）和相对湿度为98%，91%，84%的环境箱（恒定湿热实验箱，SH010）中进行吸湿实验。每隔24h将试样取出，用滤纸擦干表面水分后，立即用电子天平（上海越平科学仪器有限公司，FA2004B，精度0.01mg）称重，记录测量结果Wi。称重后将试样迅速放回环境箱中。使用式（1）计算和记录每个时间间隔的相对质量增量。当间隔24h的平均吸湿量的变化小于0.01%时，可认为材料达到有效吸湿平衡，记录有效吸湿平衡量Mm。

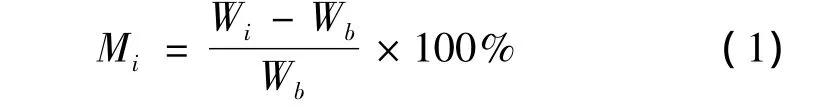
式中，Wi为i时刻试样的质量/g;Wb为吸湿前试样的质量/g;Mi为i时刻试样的相对质量增量/%。

2 实验结果

图1为不同湿度条件下的吸湿曲线，其中每个点代表每组试样的平均相对质量增量。可以看出，各湿度条件下的吸湿曲线的变化规律相似，吸湿过程表现为两个阶段:第一阶段，材料的吸湿速率较快，其相对质量增量与时间的平方根呈线性增加关系;第二阶段，材料的吸湿速率明显变缓，随着时间的增加，吸湿量逐渐趋于平衡。这表明T700/9916材料的吸湿行为是Fick扩散过程。由于水浸实验进行的时间较长，其相对质量增量已趋于平衡。随着相对湿度的增加，有效平衡吸湿量明显增大，其中水浸组的有效吸湿平衡量远大于其他三组。

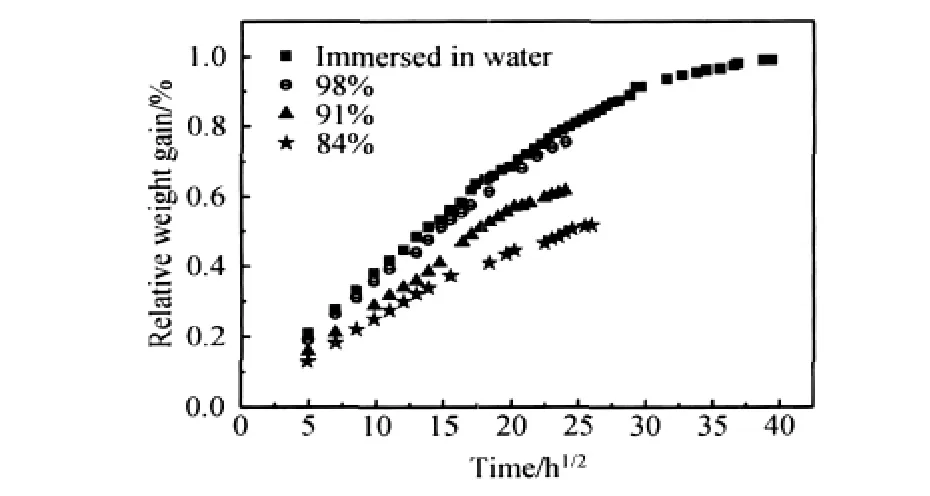
图1 不同湿度条件下的吸湿曲线Fig.1 Water-sorption curves at different relative humidity condition

根据标准［10］，假设材料沿试样厚度方向的吸湿性能不变。可使用式（2）计算沿厚度方向的扩散率Dz，计算结果如表1所示。

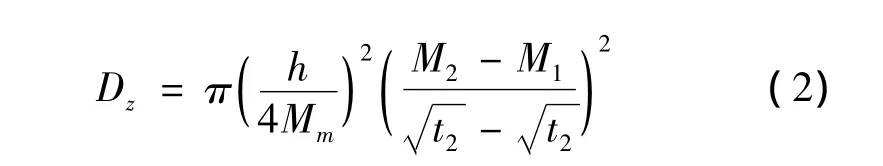
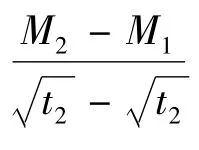
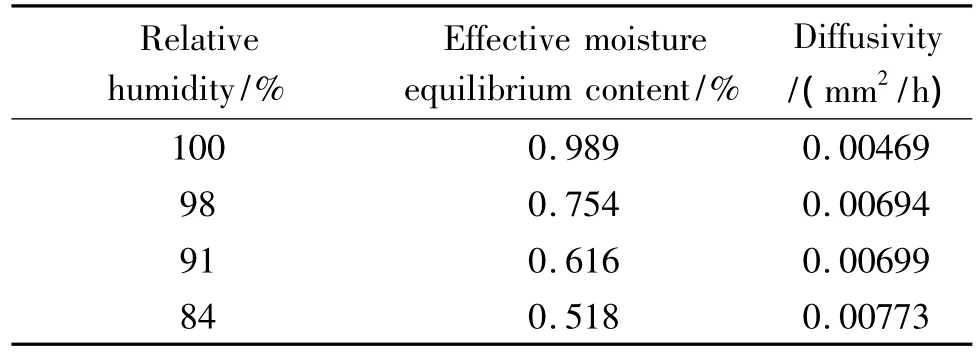
表1 不同湿度条件下扩散率的理论计算结果Table 1 Diffusivity of theoretical results at different relative humidity conditions

根据Shen C H和Springer G S等人［7］的研究，假设材料内部的温度和扩散率恒定，并且试样只从沿厚度方向的上下表面吸湿，其他侧表面不吸湿。则扩散过程的相对质量变化可由以下方程描述:

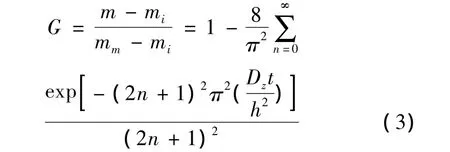
式中，m表示任意时刻试样的吸湿量/g;mm表示材料饱和吸湿量/g;mi表示吸湿前试样内的水分质量/g;t表示时间/h;z表示z方向坐标轴;h表示试样厚度/mm;Dz为沿厚度方向的扩散率/（mm2/h）。将表1中的吸湿参数代入式（3），可以得到理论吸湿量与时间的关系。图2为98%相对湿度组的理论吸湿量与实验数值。如图所示，理论结果与实验数值变化趋势相似，然而理论结果整体上比实验数值偏小。这是由于在式（3）的假设中忽略了侧面吸湿的“边缘”效应，只关注从试样上下表面进入的水分。而实际实验中的试样具有4mm的厚度，水分会从侧面扩散进入试样，因此，实验数值比理论结果整体偏大。其他各组也出现相似情况，因此采用该公式无法较好地拟合本实验结果。

3 有限元模拟

3.1 有限元分析模型

采用有限元软件ABAQUS的质量扩散模块进行计算。通过计算得到各个湿度条件下CFRP材料随时间变化的相对质量增量，并对比吸湿实验结果来验证计算模型的可靠性。

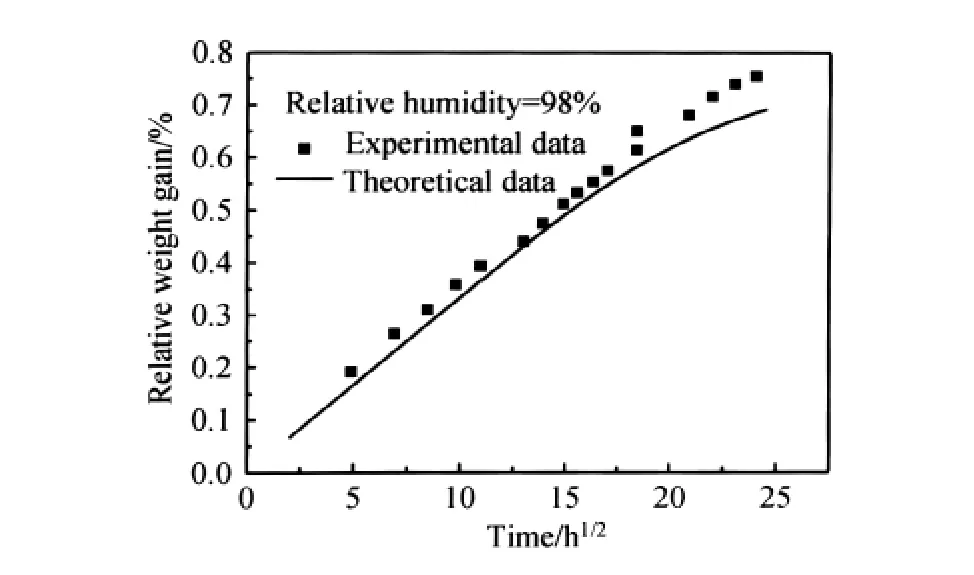
图2 相对湿度为98%条件下的实验结果和理论吸湿数据的对比Fig.2 Comparison between experimental data and theoretical data at relative humidity of 98%

由于在实验过程中试样上下表面和侧表面都会通过扩散吸收水分，因此不对有限元模型结构进行简化。试样铺层方式为［+45/0/-45/90］4S，为简化计算，将方向相同的铺层看作1个铺层处理。网格划分的单元类型为DC3D20，整个有限元模型的网格参数为:节点总数108397，单元总数240000。

3.2 有限元模拟吸湿参数的设定

3.2.1 吸湿参数的计算

ABAQUS中质量扩散模块的控制方程是Fick方程的扩展形式，其表达式为式（4）。

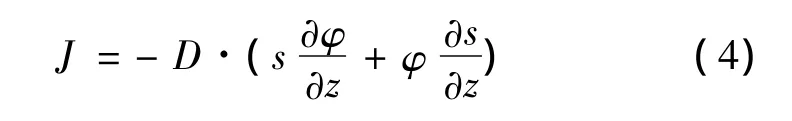
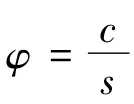
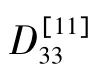
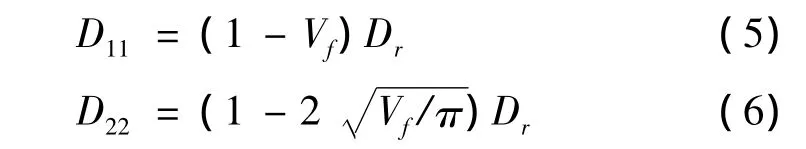
其中Vf为纤维体积分数;Dr为基体的扩散率。

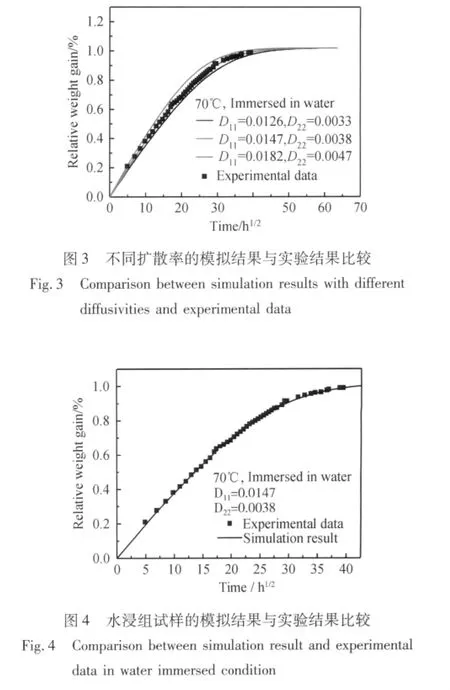
由于水浸组的实验进行时间较长，相对质量增量已趋于平衡。取水浸组实验数据进行模拟，以获得材料的扩散率D11，D22和D33。其中，溶解度系数s=1.02。根据实验值和一维Fick模型的计算结果假设一系列扩散率进行试算，计算结果如图3所示。对各组模拟结果与实验数据进行方差分析，选取差值最小的一组为D11=0.0147mm2/h，D22=D33=0.0038 mm2/h。模拟结果如图4所示。

由于扩散率仅随温度变化［5］，选用同一组扩散率对84%湿度的吸湿过程进行模拟。根据实验结果选取一系列溶解度进行试算。计算结果如图5所示。对各组模拟结果与实验数据进行方差分析，选取差值最小的一组为s=0.65。模拟结果如图6所示。

3.2.2 吸湿参数的确定

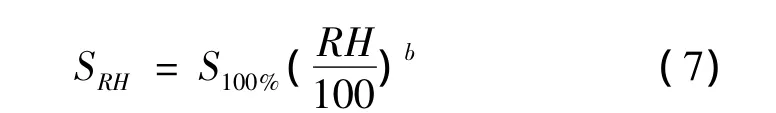
在相同温度下，对于暴露于湿空气的材料，其饱和吸湿量与空气的相对湿度之间的关系可以表示为［7］:式中，SRH代表湿空气中材料的饱和吸湿量/%;S100%代表水浸时材料的饱和吸湿量/%;b为常数;RH为空气相对湿度/%。

根据水浸组和相对湿度为84%组的计算结果，已经知道其各自条件下材料的饱和吸湿量为1.02%和0.65%。根据式（7）可以计算得到常数b=2.64。再次通过式（7）可以计算相对湿度为91%和98%条件下的饱和吸湿量分别为0.795%和0.967%。

3.3 吸湿行为的有限元模拟

将3.2节计算得到的扩散率和饱和吸湿量带入模型中，分别计算相对湿度为98%和91%的吸湿曲线，结果如图7所示。各组模拟结果与实验数据拟合较好，验证了吸湿参数的有效性。采用这种方法可以对该材料进行不同湿度下的模拟，并获得长期的吸湿动力学曲线，弥补了实验方法周期长的弊端。

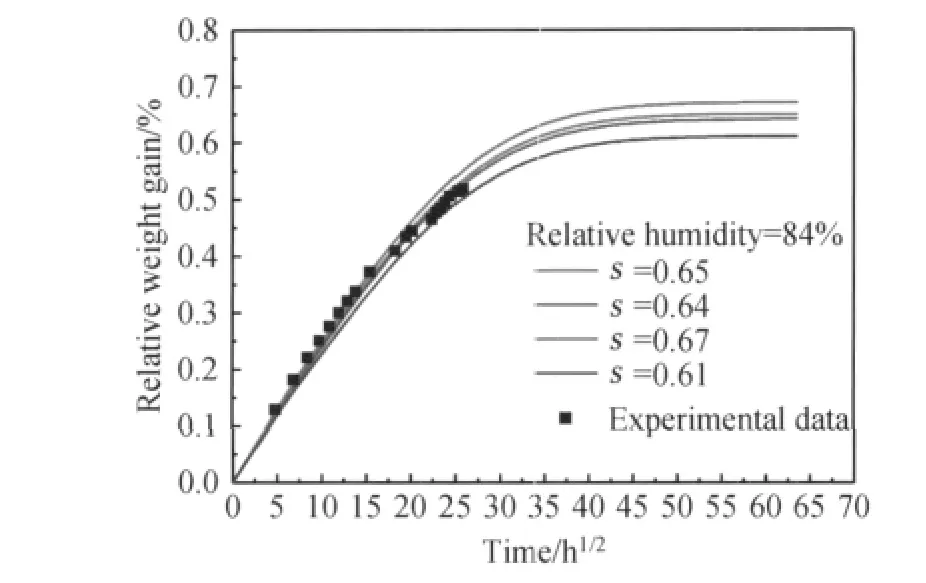
图5 不同溶解度的模拟结果与实验结果比较Fig.5 Comparison between simulation results with different solubility and experimental data

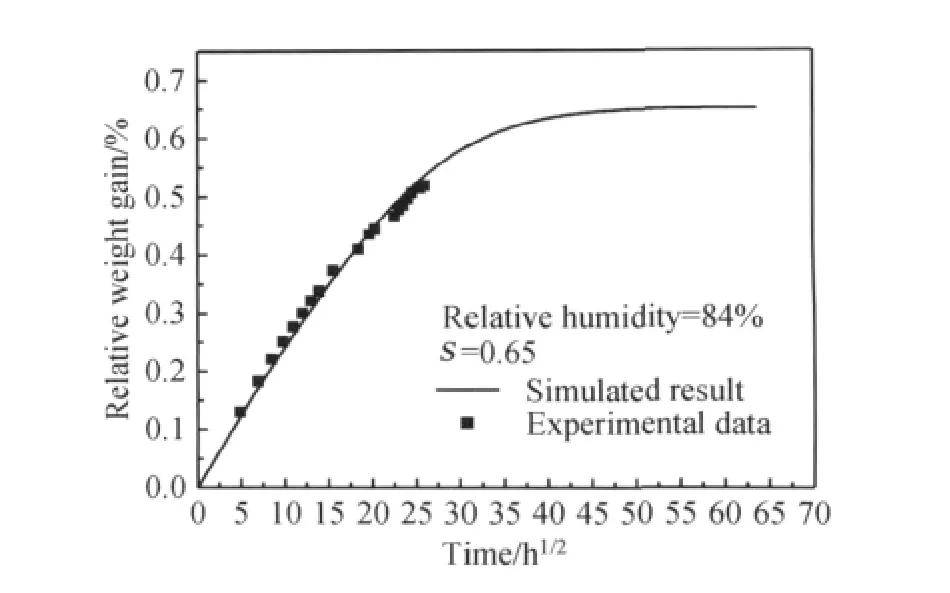
图6 相对湿度为84%的模拟结果与实验结果比较Fig.6 Comparison between simulation result and experimental data at relative humidity of 84%

将不同条件下计算得到的饱和吸湿量与实验得到的有效吸湿平衡浓度比较，如表2，可以发现各组实验值均比饱和吸湿量小。因为根据标准［10］进行的吸湿实验仅要求间隔24h的相对质量增量小于0.01%时即达到平衡，而实验结果表明，达到该标准时，较低湿度条件下的吸湿曲线仍处于线性增加阶段。这是由于本组实验采用的试样厚度较大，当达到标准中的有效吸湿平衡时，材料内部的水分还未分布均匀，促进水分子扩散的浓度梯度仍然存在。因此，以后的实验工作应适当延长吸湿时间，以获得更加有效的实验参数。

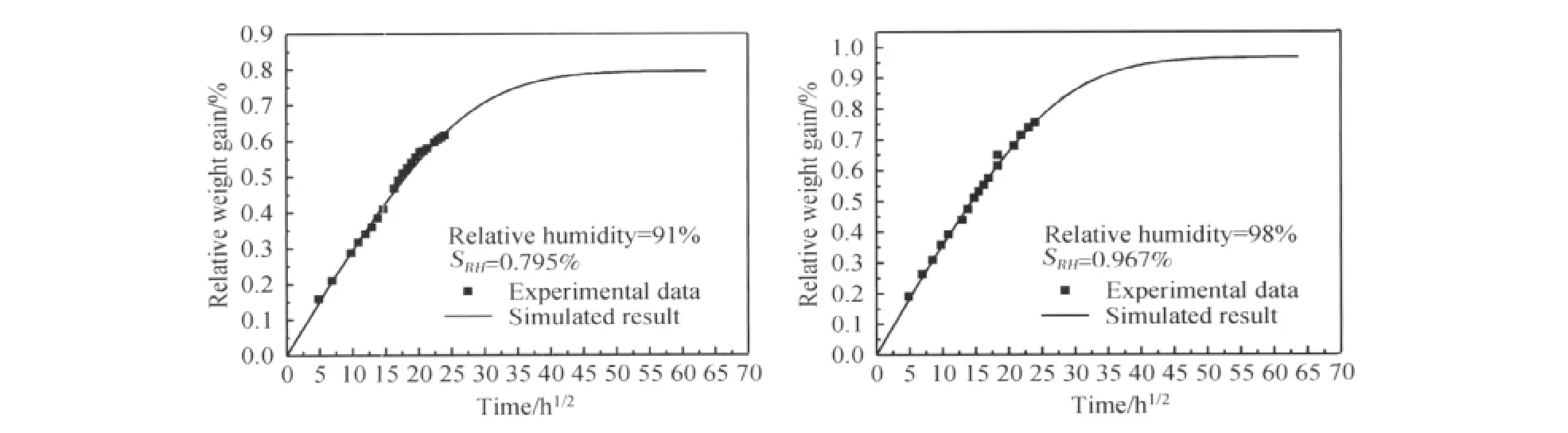
图7 相对湿度为91%和98%的模拟结果与实验结果比较Fig.7 Comparison between simulation results and experimental data at relative humidity of 91%and 98%

表2 饱和吸湿量与有效吸湿平衡浓度比较Table 2 Comparison between solubility and effective moisture equilibrium content

3.4 有限元模拟结果

采用有限元方法不仅可以通过短期实验获得材料长期的吸湿动力学曲线，还能得到材料内部的水分分布情况。图8为水浸组试样在不同时刻的水分分布情况。直接接触湿环境的材料表面在吸湿初期就迅速达到饱和吸湿浓度。在不同的吸湿时刻，试样截面由边缘向中心的水分浓度场颜色逐渐变浅，表明水分浓度沿边缘向内部逐渐减少，这与Mercier J等人［12，13］的研究结果相似。随时间的增加试样内部的水分浓度逐渐增大，这是水分子扩散的结果;当时间增加到1490h左右，水分子得到充分扩散，可以看出试样截面已呈均匀的灰度，表明试样内部均达到饱和吸湿浓度，这时材料达到平衡吸湿状态。

图9为t=1490h时不同吸湿条件下试样内部的水分分布情况。此时水浸组试样已达到吸湿平衡，而其他吸湿条件的试样截面仍然呈现不均匀灰度，表明还未达到平衡吸湿。从图中可以看出其他三组试样表面都已达到各自条件下的饱和吸湿浓度，分别为0.967%，0.795%和0.65%，这是试样表面直接接触湿环境的结果;而由于水分子扩散不充分，试样中间的浓度仍较小，远没有达到饱和吸湿状态。

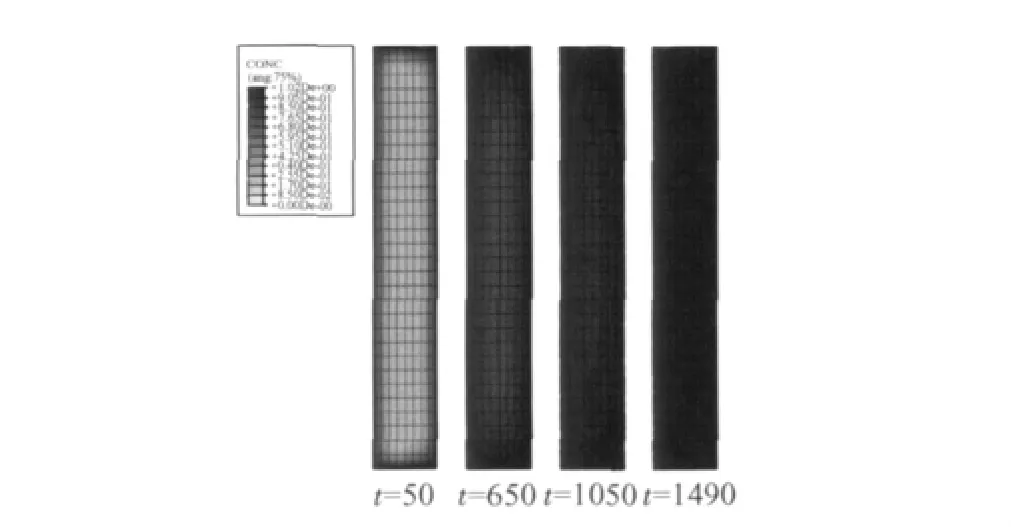
图8 在不同时刻水浸组试样内部的水分分布图Fig.8 Moisture distribution within specimen immersed in water at different time

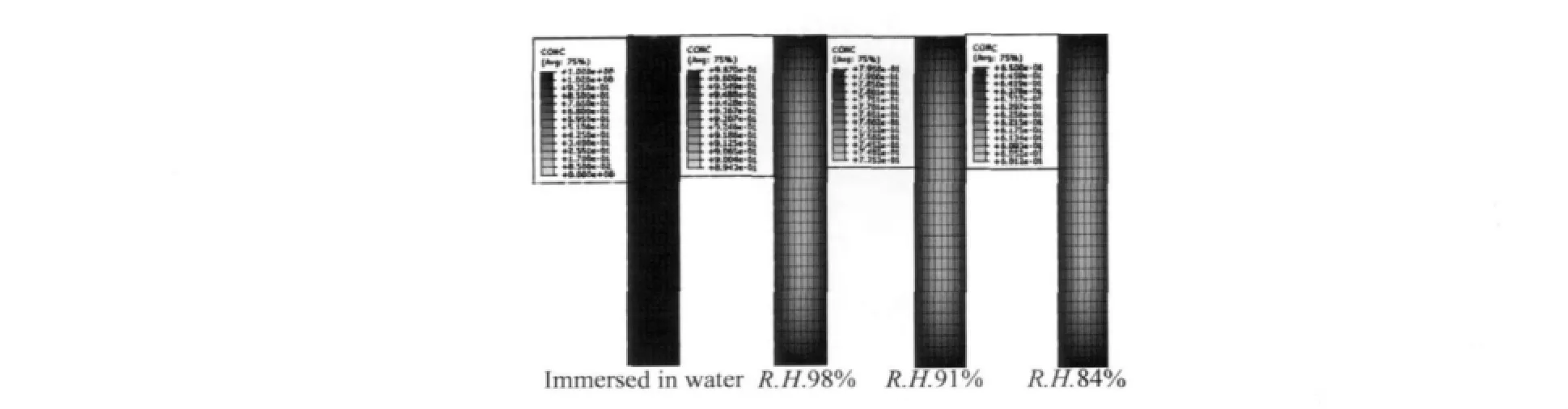
图9 t=1490h时不同吸湿条件下试样内部的水分分布情况Fig.9 Moisture distribution within specimens at different conditions at t=1490h

4 结论

（1）根据ASTM D 5229/D 5229M—1992（2004）标准对T700/9916复合材料层合板在相同温度不同湿度条件下进行吸湿实验，实验得到的有效吸湿平衡浓度比材料的饱和吸湿量小，较低湿度条件下的实验数据仍处于线性增加段。

（2）根据实验数据，通过插值法和有限元模拟软件ABAQUS计算获得材料的扩散率及其在不同条件下的溶解度系数，利用该系数对吸湿实验结果进行模拟，模拟结果与实验结果吻合较好。

（3）采用有限元方法可以获得材料的吸湿动力学曲线和试样内部水分分布情况，并能预测材料的长期吸湿行为。不同湿度条件下材料达到吸湿平衡的时间不同:水浸组试样经过约1490h达到平衡吸湿状态，试样内部水分浓度分布均匀，各点都达到饱和吸湿量1.02%;而此时其他各组还未达到吸湿平衡状态。

［1］陈祥宝.先进树脂基复合材料的发展［J］.航空材料学报，2000，20（1）:20-21.

［2］US Army Research Laboratory，Weapons and Materials Research Directorate.MIL-HDBK17-1F Composite materials handbook［S］.Philadelphia:the Document Automation and Production Service，2002.

［3］MCKAGUE E L，REYNOLDS J D，HALKIAS J E.Life assurance of composite structures:AFML-TR-75-51:Vol 1［R］.Ohio:AFML（LC），Wright-Patterson AFB.1975.

［4］BONNIAU P，BUNSELL A R.A comparative study of water absorption theories applied to glass epoxy composites［J］.Journal of Composite Materials，1981，15（3）:272-293.

［5］IMAZ J J，RODRIGUEZ J L，RUBIO A.Hydrothemal environment influence on water diffusion and mechanical behavior of carbon fibre/epoxy laminates［J］.Journal of Materials Science Letters，1991，10（11）:662-665.

［6］郑路，常新龙，赵锋，等.湿热环境中复合材料吸湿性研究［J］.纤维复合材料，2007（2）:37-39.

［7］SHEN C H，SPRINGER G S.Moisture absorption and desorption of composite materials［J］.Journal of Composite Materials，1976，10（1）:2-20.

［8］PAVANKIRAN V，TOSHIO N，RAMAN P S.Inverses analysis for transient moisture diffusion through fiber-reinforced composites［J］.Acta Materialia，2003，51（1）:177-193.

［9］孙丽.纤维增强环氧树脂基复合材料吸湿行为的有限元研究［D］.天津:天津大学，2007:38-52.

［10］American SocietyforTestingand Materials. ASTM D5229/D 5229M Standard test method for moisture absorption properties and equilibrium conditioning of polymer matrix composite materials［S］.PA:ASTM International.1992.

［11］ABAQUS User Manual，Dassault Systems［C/CD］.Rhode Island:H:Bbitt，karlsson＆ Sorensen，Inc.2008.

［12］MERCIER J，BUNSELL A，CASTAING P.Characterization and modeling of aging of composites［J］.Composites（A），2008，39（2）:428-438.

［13］BOUKHOULDA B F，ADDA-BEDIA E，MADANI K.The effect of fiber orientation angle in composite materials on moisture absorption and material degradation after hydrothermal ageing［J］.Composite Structures，2006，74（4）:406-418.