基于FPGA的RBF神经网络的硬件实现
王兴
(武汉科技大学 信息科学与工程学院,湖北 武汉430081)
人工神经网络广泛应用于图像处理、模式识别和自动控制等领域。但是,传统的基于软件实现的神经网络,存在并行程度低、速度慢,计算速度无法满足实时性的需求,造成了理论研究与实际应用脱节。因此,神经网络的硬件实现是神经网络研究的基本问题之一。神经网络的硬件实现的最大特点就是体现了系统的并行性,处理速度快,易于满足实时性要求。另外,算法的复杂程度以及在实际工程中应用的可行性仍需要通过硬件的实现效果来检验。因此,神经网络的硬件实现意义重大。
1 RBF神经网络的简介
径向基函数 (Radial Basis Function,RBF) 网络是由Moody J和Darken C于20世纪80年代末提出的一种神经网络结构,是一种有监督的神经网络。它是借鉴生物机制中的局部调节及交叉接受区域知识的基础上提出的一种采用局部接受域来执行函数映射的人工神经网络。RBF网络最基本的构成包括3层,其结构如图1所示,其中每一层都有着完全不同的作用。
输入层由一些源点(感知单元)组成,他们将网络与外界环境连接起来;第二层是网络中仅有的一个隐层,它的作用是进行从输入空间到隐层空间的非线性变换。隐层节点中的

图1 RBF神经网络结构图Fig.1 Structure diagram of RBF neural network
作用函数(基函数)对输入信号将在局部产生响应,也就是说,当输入信号靠近基函数的中央范围时,隐层节点将产生较大的输出,由此看出这种网络具有局部逼近能力。输出层是线性的,它为作用于输入层的激活模式(信号)提供响应。
径向基函数有多种形式,如:二次型、逆二次型或Gauss型等。若采用高斯函数作为径向基函数,则神经元的输出为:
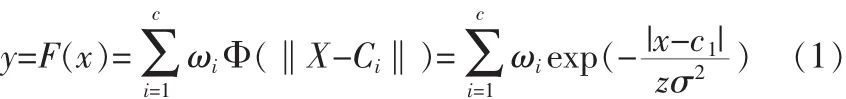
上式中,m是隐含层结点数;‖·‖是欧几里德范数;Ci和σi分别为与每个隐含层节点相关的参数向量的中心和宽度;ωi是第i个基函数与输出结点的连接权值。
2 RBF网络的FPGA实现
2.1 RBF单元中心Ci和半径σi的确定
对各RBF的中心及半径的确定通常有以下两种方式:
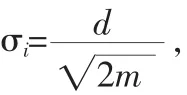
2)用聚类方法,把样本聚成几类,以类中心为各RBF函数的中心。
首先,中心Ci的确定。采用k-均值聚类分析技术确定Ci。找出有代表性的数据点 (不一定位于原始数据点)作为RBF单元中心,从而极大地减少隐RBF单元数目,降低网络复杂化程度。利用k-均值算法获得各个聚类中心后,即可将之赋给各RBF单元作为RBF的中心。
然后,半径σi的确定。半径σi决定了RBF单元接受域的大小,对网络的精度有极大的影响。半径选择的原则是使得所有RBF单元的接受域之和覆盖整个训练样本空间。
通常应用k-均值聚类法后,对每个聚类中心Ci,可以令相应的半径σi等于与其属于该类的训练样本之间的平均距离,即
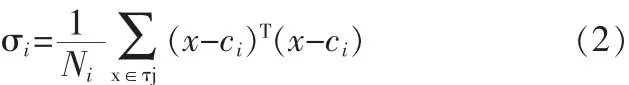
2.2 调节权矩阵W
这里权W是指输出层和隐层之间的权值,可以采用线性最小二乘法和梯度法来调节权矩阵W。
1)线性最小二乘法。令网络输出为
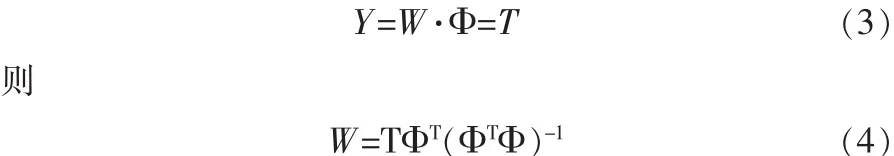
2)梯度法。迭代公式如下:
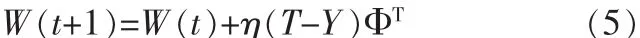
由于输出为线性单元,因而可以确保梯度算法收敛于全局最优解。所以,在本设计中采用梯度法来修改权值W。
2.3 隐层非线性函数映射的实现
RBF神经网络隐层中的映射函数为高斯函数,为非线性函数。而非线性函数在硬件上实现往往比较复杂,难度较大。通常实际工程中采用查表法或迭代法来近似模拟这些非线性函数,查表法较迭代法虽在结构和运算复杂度上有明显降低,但在精度上也会明显降低。若要提高精度,只能增加表的大小,但增加表的大小,直接带来的影响就是会加大存储空间和降低查表效率,所以,在FPGA上采用何种方法实现高斯函数的存储达到精度和效率之间的平衡就至关重要。
高斯函数表达式为

2.3.1 STAM算法
STAM算法的主体思想是先产生系数,然后利用系数的对称性减小ROM表的大小。在该算法中先把输入X分为m+1 个部分:x0,x1,…,xm。 则 f(x)可以近似为

该种方法虽然在某种程度上使得查找表的数量增加了,但每个表的大小却大大减小了,整体上查找表还是减少了,效率上也相应提高了。
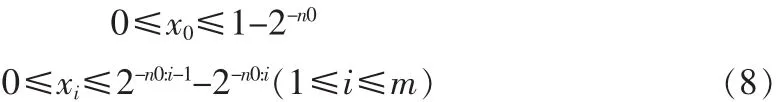
为了减小表的误差和在表系数中构造对称,定义δi以恰好位于xi的最大值和最小值的中间,即:f(x)在 x0+x1+x2:m 点的二阶泰勒级数展开为:用δ1代替上式第2部分中的x1:



然后再把第2部分分开:
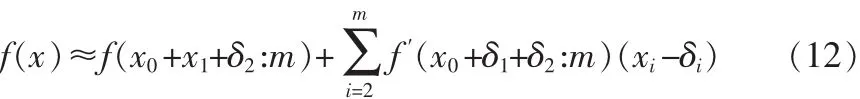
和式(1)比较,就可以确定系数为:
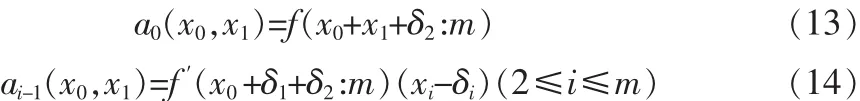
式(13)构造的查找表 a0(x0,x1),其输入值的位数为 n0+n1。式(14)所构造的其余 m-1 个查找表 ai-1(x0,xi),由于 δi被定义为xi的取值区间的中间点,故查找表中的系数值具有对称性,即 ai-1(x0,xi)与 ai-1(x0,2δi-xi)互为补码,其输入值的位数可以减为n0+n1-1,从而使这m-1个查找表的存储空间节省了一半。
2.3.2 CORDIC迭代法
坐标旋转计算机 (CORDIC:Coordinate Rotation Digital Computer)由 Volder.J于 1959 年提出[1],1971 年 J.S.Walther提出统一CORDIC算法[2]。
该算法是用于计算一些常用的非线性函数的循环迭代算法。其基本思想是用一系列与运算基数相关的角度的不断偏摆从而逼近所需旋转的角度,从而达到非线性函数的逼近。
由 CORDIC算法可知,计算指数函数 exp(x)的迭代公式为:
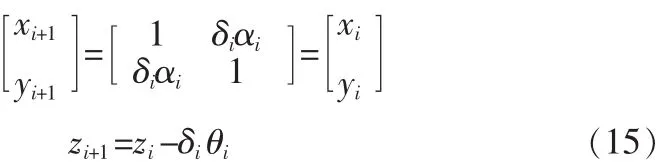
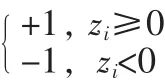
迭代n次后的结果为
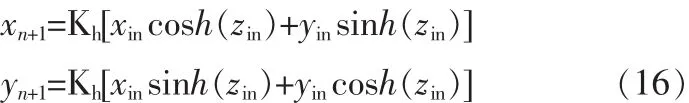

在实现指数函数exp时,采用MATLAB仿真与CORDIC迭代结合的方式。因为迭代过程中有限字长的截断将造成截断误差,所以如果 CORDIC输入数据为 N bit,则x,y迭代过程需log2(N)的保护位。具体迭代过程为:首先,把CORDIC输入数据映射到CORDIC迭代收敛区间,并根据相应数值的某位数字寻址查表;然后,以为z路径的初始值按公式(15)进行CODIC 迭代,直到满足迭代次数,此时得到 xi为 Kh·exp(zin)。
2.4 系统整体设计框图
RBF神经网络训练部分的系统框图如图2所示。
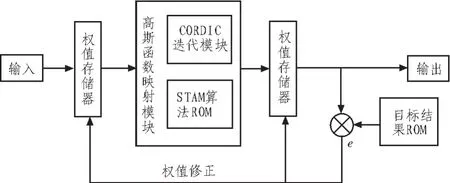
图2 系统整体设计框图Fig.2 Structure diagram of the whole system
3 系统仿真
本实验以Altera公司开发的 EDA工具QuartusⅡ作为编译、仿真平台 ,选用Cyclone系列中的 EP1C6Q240C8器件。且以经典非线性问题XOR问题为算例。仿真结果如表1所示。
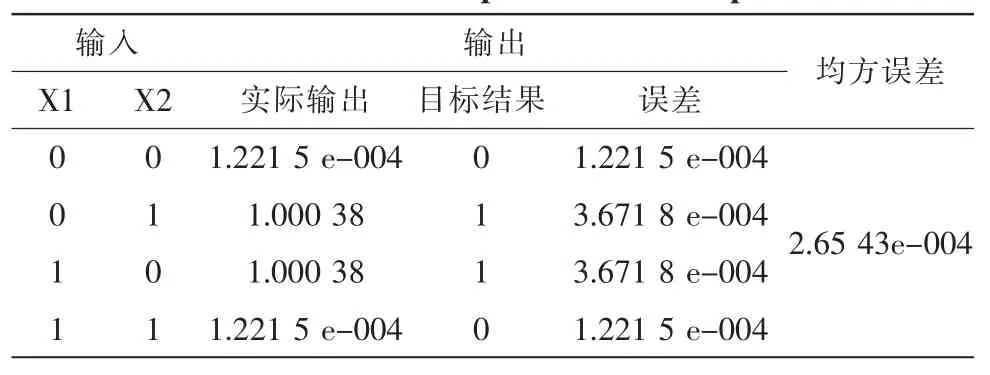
表1 XOR实验仿真结果Tab.1 Test result of experimet on XOR problem
4 结束语
FPGA作为一种可编程资源,在提高设计灵活性及加快算法效率上,比较适合硬件实现神经网络 ,可以加快。而文中采用STAM算法,可以有效地节省存储空间 ,且CORDIC迭代算法实现了RBF网络中的非线性高斯映射函数,所耗资源较少,适合于作为硬件实现网络的算法。从经典非线性XOR算例在基于文中所设计的RBF网络中有较好结果,不仅精度上得到较满意的结果,且网络的总体误差也较小。
[1]Volder J E.The CORDIC trigonometric computing technique[J].IRE Trans.on Electron Computing,1959(8):330-334.
[2]Walther J S.A unified algorithm for elementary functions[J].Proc.AFIPS Conference,1971(38):389-385.
[3]Hu X,Harber R G,Bass S C.Expanding the range of convergence of the CORDIC algorithm[J].IEEE Transactions on Computer s,1991,40(1):13-21.
[4]Y.H.The quantization effects of the CO RDIC algorithm[J].IEEE Transaction on Signal Processing,1992,40(4) :57-63.[5]Andraka R.A survey of CORDIC algorithms for FPGA based computers[C]//Proc.of the 1998 ACM/SIGDA sixth international symposium on FPGA,1998.
[6]Takagi N,Asada T,Yajima S.Redundant CORDIC methods with a constant scale factor for sine and cosine computation[J].IEEE Trans.Computers,1991(40):989-995.
[7]Wang S,Piuri V,Swartzlande E E.Hybrid CORDIC algorithms[J].IEEE Trans.Computing,1997(46):1202-1207.
[8]Dou Y,Vassiliadis S,Kuzmanov G K,et al.64-bit floatingpoint FPGA matrix multiplication[C]//Proceedings of the 2005ACM/SIGDA 13th international symposium on Fieldprogrammable gate arrays,2005:86-95.

